一种小天体旋转参数估计方法*

刘 鹏， 倪郑鸿远， 赵 巍*， 王志强

0 引 言

从第一颗人造卫星的升空到成功踏上月球的土地，人类对外太空的探索取得了可观的成绩如今，人类已将探索的目光从大型天体转向小行星、彗星等小天体.近几十年来，美国、日本、欧空局都相继开展了小天体探测任务[1-4].

由于小天体体积小、距离地球遥远，无法在地球上得到其物理参数、形状以及表面细节的可靠估计，并且由于小天体形状不规则，观测难度大，探测器很难获取其大量的高分辨率的图像，所以利用图像中小天体的轮廓信息来恢复三维模型的方法具有重要的研究意义.对小天体旋转参数的估计包括旋转轴方向估计和自转角速度估计，典型方法包括光变曲线法和视觉运动参数估计法.用光变曲线估计小天体的旋转参数假设小天体为椭球体，通过光变曲线的变化估计小天体的旋转轴指向和自转速度.物体运动参数估计也是计算机视觉中的一项重要研究内容，在探测器导航着陆、目标跟踪等方面都会涉及到这一问题.

本文研究一种基于小天体探测接近过程中使用图像上特征点跟踪和扩展卡尔曼滤波器的小天体旋转参数估计方法.该方法首先建立小天体旋转关系模型，表示小天体在相机坐标系中的姿态变化；然后定义小天体旋转的状态方程，通过对观测图像序列上的特征点跟踪，利用扩展卡尔曼滤波器方法得到小天体旋转轴指向和自转角速度估计.在实验中，分析了相机坐标系小天体坐标系之间的四元数初值，图像上特征点跟踪精度，相机的观测指向等因素对小天体旋转参数估计精度的影响.实验结果表明，本文提出的基于图像特征点跟踪和扩展卡尔曼滤波器的小天体旋转参数估计方法能够得到具有较高精度的估计结果.

1 相关工作

1.1 基于光变曲线的小天体旋转参数估计

当小天体在视野中成像为小面积扩点目标状态时，探测器相机无法观察到小天体的轮廓形状和具体细节，此时光变曲线的信息可以为旋转轴的估计提供参考.假设小天体的形状用椭球体表示，记椭球体的三个半轴长度分别为a,b,c且a≥b≥c，假设c为旋转轴可以使椭球体的动能最小，即处于稳定状态.在入射光为平行光且能量相同的情况下，小天体的反射亮度会与其视截面的面积大小成正比，而其视截面的面积大小会随着小天体的旋转呈周期性变化.同时，当相机的视线方向与小天体旋转轴的夹角发生变化时，视截面的面积也会发生相应的变化，进而导致光变曲线的结果不同.通过光变曲线的振幅反演可以得到小天体的旋转轴指向和旋转周期[5].

1.2 基于视觉的旋转参数估计方法

运动参数估计是计算机视觉领域的一项重要的研究内容，在相机标定、探测器导航着陆、目标跟踪等方面都会涉及到这一问题.按照估计的原理可以分为直接法、光流法和基于特征的方法三类[6].

直接法是最简单的运动参数估计方法，它既不需要提前进行特征提取和匹配也不需要计算光流，直接利用图像中每个像素点的亮度来估计物体的运动.文献[7]提出了一个直接利用亮度梯度来估计物体运动信息的方法，该方法对两帧图像选择一个任意的固定点，这个点包含一个面片(patch)和对应的速度.通过解算两个线性方程组，可以得到像素平移参数，将这些平移参数应用于第二帧图像中的每一个像素点就得到了固定的第二帧图像.最后求解3×3矩阵的特征值和特征向量，利用最小特征值对应的特征向量，第一帧图像以及固定的第二帧图像可以求出平移方向、旋转速度和相对深度.Heel提出了基于卡尔曼滤波器的直接估计场景结构和相机相对于场景的位姿的方法.随着时间的推移，卡尔曼滤波器可以逐渐地提升预测的效果.在更新阶段，卡尔曼滤波器会结合当前的深度估计和测量值对估计做出校正.

Gibson提出了光流的概念：物体在空间中运动，由相机成像后，图像上像素运动的瞬时速度称为光流.对场景中的运动物体进行连续拍摄得到图像序列，相邻图像中物体运动具有一定的相关性，光流法利用这种相关性，通过分析像素随时间产生的变化，可以计算出物体的运动信息.根据引入的约束条件的不同，分析方法也不同，例如基于梯度的Lucas-Kanade算法[8]、区域匹配法等.由于光流法假设物体亮度不变，且计算量较大无法进行实时预测，所以较难应用于小天体的运动参数估计中.

基于特征的方法是目前位姿参数估计领域的研究热门，也是成功应用于小天体运动参数估计的方法，首先要从图像中提取的特征，然后进行特征匹配，根据跟踪的特征点信息来估计物体的运动参数.根据使用的特征的不同，方法的适用场景也不相同.常用的特征提取算法可以分为尺度不变特征点算法和角点特征点算法.SIFT特征[9]是尺度不变特征检测算法的代表，这一类特征的优点是对图像的尺度、旋转以及亮度变化不敏感，但是执行效率较低；而以Harris角点算法计算简单，但是由于不具有尺度不变性.基于特征的方法可以分为两类：批处理算法和递归算法.批处理算法不满足实时性，而递归算法只需要上一次的状态估计和当前的测量值，就能得到当前的状态估计，占用的存储资源少，执行效率高.BROIDA提出了基于循环扩展卡尔曼滤波器(IEKF)的递归算法[10].IU等人提出的方法将旋转平移表示为任意阶多项式的形式，将问题转化为多项式系数的估计问题[11].

2 小天体旋转参数估计

2.1 姿态表示和观测方程

小天体旋转参数估计主要涉及三个坐标系：世界坐标系Ow-XYZ、小行星坐标系OS-xyz、相机坐标系Oc-xyz，如图1所示.

图1 坐标系的定义Fig.1 Definition of coordinate systems

用四元数表示相机坐标系与小天体坐标系之间的姿态关系.对于一个四元数q，其数学代数形式为：q=q1+iq2+jq3+kq4，去满足正交化约束

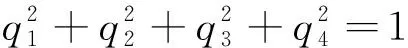
(1)

设t时刻小天体坐标系原点Os在相机坐标系Oc-xyz中的坐标定义为

S0(t)=[x0(t)y0(t)z0(t)]T

(2)

在小天体坐标系OS-xyz中的小天体表面一点Si0,i=1,2,…,M,M为特征点的数量.在相机坐标系Oc-xyz中的坐标可以表示为：

Si(t)=S0(t)+R(t)Si0(t)=[xiyizi]T

(3)

t时刻Si(t)对应的图像坐标为：

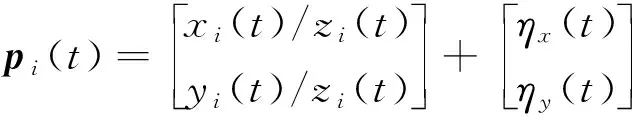
(4)

2.2 状态变量和状态方程

M个特征点在小天体坐标系中的坐标表示为：

[x1y1z1]T,[x2y2z2]T,…,[xMyMzM]T

定义状态变量s(t)：

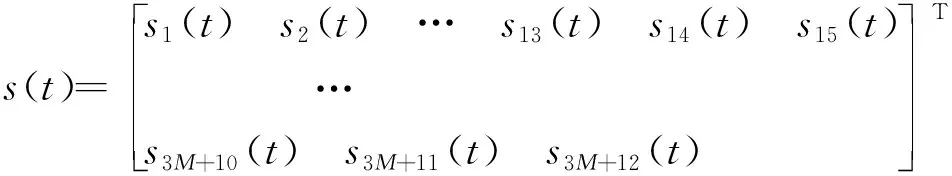
(5)

状态变量的描述将表1.

表1 状态变量的描述Tab.1 Description of state variables

状态变量中包含了小天体和相机之间的旋转关系，在相机坐标系下的小天体坐标系原点位置、角速度和线速度，以及选取的特征点在小天体坐标系下的位置.利用小天体坐标系原点在相机坐标系下的z轴位置z0(t)作为状态变量中所有坐标的归一化因子.定义了状态变量s(t)后，小天体位移-旋转状态转移方程可以用式(6)表示：

st+1=f(st)+wt

(6)

其中wt为均值为0，协方差矩阵为Qt的高斯随机噪声，f(·)为状态转移函数.状态变量的微分近似为：

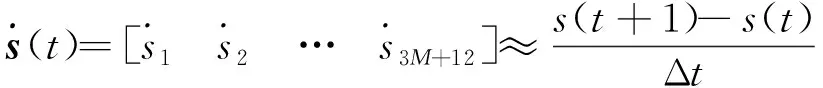
(7)

其中：

=s3(t)-s1(t)s5(t)

=s4(t)-s2(t)s5(t)

=-s3(t)s5(t)

=-s4(t)s5(t)

=0.5[s12(t)s7(t)-s11(t)s8(t)+s10(t)s9(t)]

=0.5[-s12(t)s6(t)-s10(t)s8(t)+s11(t)s9(t)]

=0.5[s11(t)s6(t)-s10(t)s7(t)+s12(t)s9(t)]

=0.5[-s10(t)s6(t)-s11(t)s8(t)-s12(t)s9(t)]

…

=-s3M+1(t)s5(t)

=-s3M+2(t)s5(t)

=-s3M+3(t)s5(t)

定义测量值为M个特征点对应的图像坐标为：

p(t)=[X1(t)Y1(t) …XM(t)YM(t)]T

(8)

上式中的元素表示为：

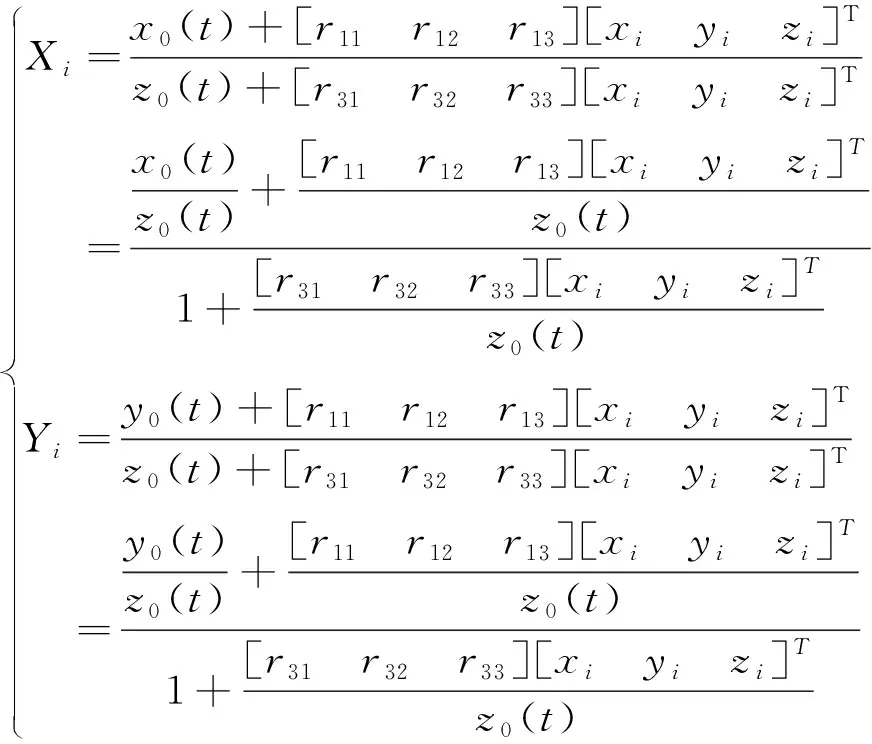
(9)

将

x0(t)/z0(t)=s1

y0(t)/z0(t)=s2

[xiyizi]T/z0(t)=[s3i+10s3i+11s3i+12]T

[r11r12r13]=

[r31r32r33]=

代入式(8)，得观测方程：

p(t)=h(st)+vt

(10)

其中vt为均值为0，协方差矩阵为Rt的高斯噪声矢量.

2.3 扩展卡尔曼滤波器估计状态

将状态转移方程(6)和观测方程(10)写成标准的扩展卡尔曼滤波器形式：

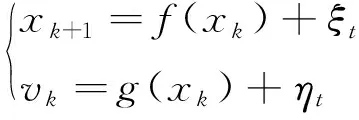
(11)

扩展卡尔曼滤波器的计算过程如图2所示：

图2 扩展卡尔曼滤波器计算过程Fig.2 Calculation process of extended Kalman filter

3 实验结果

采用真实的67彗星三维模型分别在探测器距目标100 km和20 km两种的情况下进行实验，探讨了四元数初值，图像特征点精度和相机观测方向等对于小天体旋转参数估计精度的影响.

3.1 实验条件

目标：使用67p三维模型，位于世界坐标系原点，绕z轴每帧转1°.

相机：光轴指向世界坐标系原点，渲染图像的分辨率为1024×1024，像元尺寸为8.6 μm，焦距为630.243 mm，共180帧.

特征点选取：在三维模型上选择4个特征点，如图3所示，这些特征点在小天体坐标系下的坐标：

p1(-2354 cm, 14124 cm, -4268 cm)，

p2(7581 cm, 7663 cm, -15264 cm)，

p3(-7745 cm, 2840 cm, -12237 cm)，

p4(5660 cm, 1347 cm, -19400 cm).

图3 在67p彗星上选取的特征点Fig.3 Selected feature points on comet 67p

观测值：已知特征点的三维坐标，利用三维重建后得到的相机外参数和相机本身的内参数，可以计算出特征点在每一幅图像上的坐标.

旋转轴指向误差：扩展卡尔曼滤波器预测得到的旋转轴方向与模型真实旋转轴方向的夹角(相机坐标系下).

角速度误差：模型设置的角速度与滤波器预测角速度的差值(在相机坐标系下3个坐标轴方向).每一次实验均进行100次，取结果均值.

3.2 四元数初值对旋转参数估计精度的影响

在设置67彗星坐标系到相机坐标系的三轴旋转关系为(-45°,0°,0°)，对四元数逐步加入5°、10°、20°的偏差，对67p旋转轴估计误差如图4所示.实验结果表明，在距离目标100 km时，用本文方法估计67p旋转轴指向对于四元数初值误差不敏感.

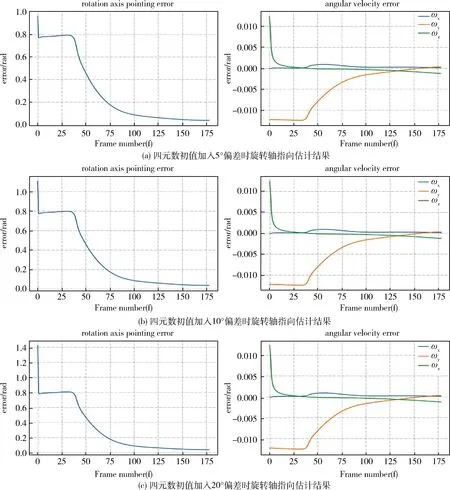
图4 相机与67p彗星相距100 km时，四元数初值对旋转参数估计精度的影响Fig.4 When the distance between the camera and comet 67p is 100 km, the effect of initial quaternion value on the estimation accuracy of rotation parameters is as follows

3.3 特征点跟踪精度对旋转参数估计精度的影响

对观测的特征点图像坐标加入均值为0，标准差分别为0.04 mm，0.08 mm，0.12 mm的高斯噪声(像素尺寸为8.6 μm)，67彗星旋转轴指向估计误差如图5所示.实验结果表明，在距离目标100 km时，特征点跟踪误差的标准差不应超过0.04 mm.

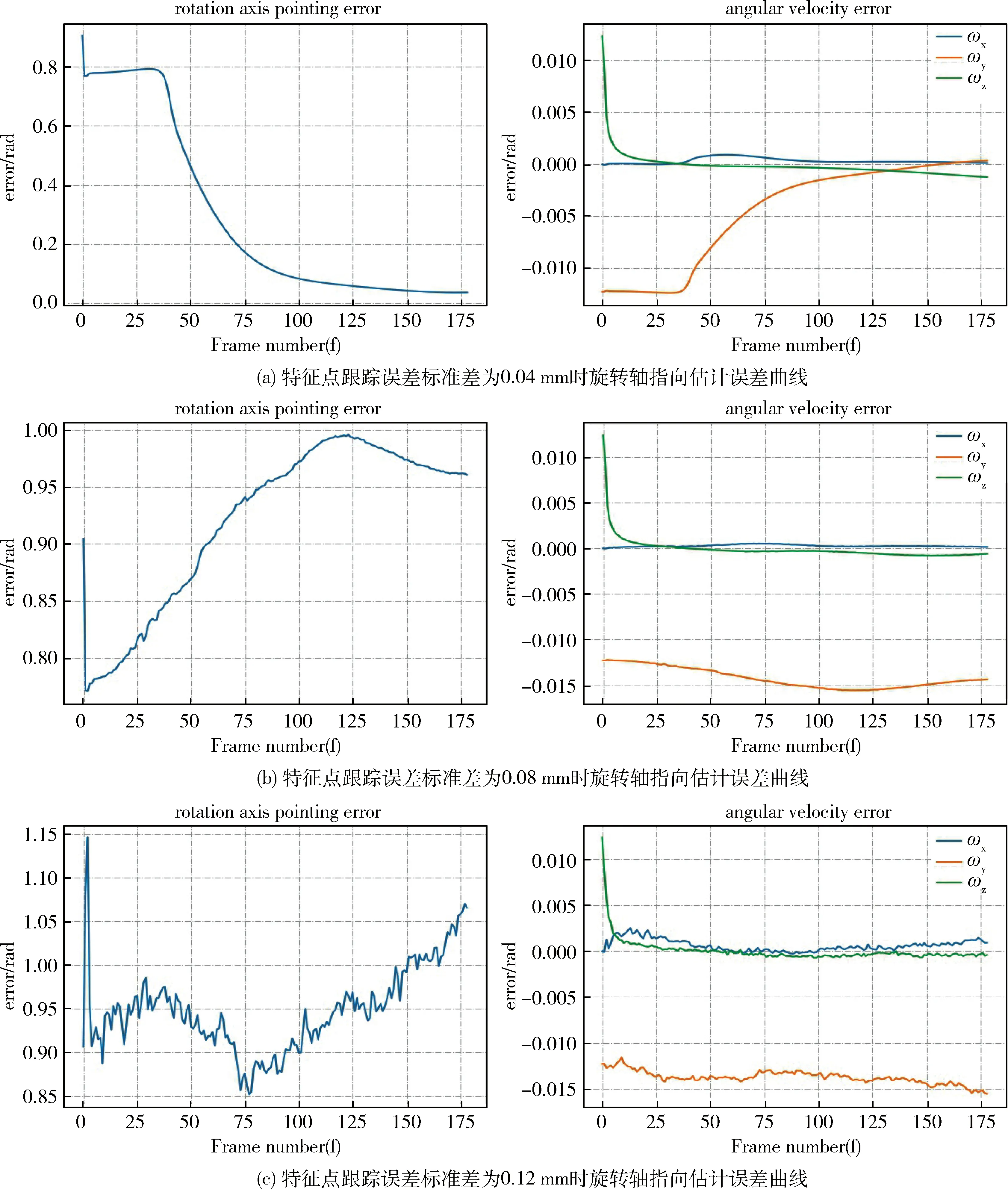
图5 相机与67p彗星相距100 km时，图像特征点跟踪精度对旋转参数估计精度的影响Fig.5 When the distance between the camera and comet 67p is 100 km, the influence of the tracking accuracy of image feature points on the estimation accuracy of rotation parameters

3.4 相机光轴方向对旋转参数估计精度的影响

假设在100 km位置已经得到关于小天体旋转轴指向，分别设置探测器在小天体坐标系以下3个位置观测：(0,0,-20 km)、(0,14 km,-14 km)、(0,20 km,0)(即与旋转轴夹角为0°、45°、90°).实验结果如图6所示.实验结果表明，在探测器距离小行星20 km时，在两极(观测方向与小天体旋转轴夹角为0°)，观测可以获得最好的估计结果，在赤道处(观测方向与小天体旋转轴夹角为90°)观测虽然也可以获得不错的结果，但是由于特征点的消失和加入导致预测过程出现波动，需要较长的迭代次数才能收敛.

4 结 论

本文研究的基于图像特征点跟踪的扩展卡尔曼滤波器小天体旋转参数估计方法，定义了用于小天体旋转参数估计的状态变量，推到了状态转移方程和测量方程，详细给出了计算过程.用67P彗星三维模型进行了实验.实验结果表明本文方法能够在相机与目标小天体相聚100 km距离时，估计出小天体的旋转参数；当相机与目标小天体相聚20 km距离时，将相机主光轴方向与小天体旋转轴方向的夹角控制在45°以内，本文方法能够鲁邦地估计小天体旋转轴指向和自转速度.