基于ANSYS后装压缩式垃圾车滑板的结构优化设计
2020-04-28邹震
邹震
福建龙马环卫装备股份有限公司 福建龙岩 364028
1 前言
随着垃圾分类的不断推广,人们对垃圾收运的节能、环保、绿色等要求也不断提高,越来越多的地方开始实行专车专用。因后装压缩式垃圾车具有装载量大、压实率高、污水防滴漏等优点,故其广泛应用于垃圾的收集与转运。滑板作为压缩机构的重要部件,运动频繁、受力集中且结构笨重,这要求其具有良好的动静态性能,以保证整车的压填性能[1]。
滑板的结构优化设计是指在满足功能要求的前提下,尽可能地提高滑板的刚度、模态频率,以及减轻滑板的质量,从而提高滑板的动静态性能和降低生产成本。如何确保提高滑板动静态性能的同时进行减重是众多工程技术人员面临的主要难题之一。
本文把滑板壁厚作为设计变量,应变、质量作为设计目标,利用ANSYS Workbench软件对滑板进行动、静态分析和关键尺寸的灵敏度分析,在提高滑板刚度、模态频率的同时进行减重,筛选出滑板壁厚的最佳尺寸。基于此方法,保证滑板动、静态性能的同时,降低了滑板生产成本,缩短了产品的研发周期,并可复制推广到其他零部件,对压缩式垃圾车的优化设计具有重要指导意义[2]。
2 构建滑板有限元模型
2.1 滑板工作原理
压缩机构如图1所示,主要由滑板、刮板、滑块、刮板油缸、滑板油缸组成。在工作过程中,刮板油缸伸出,带动刮板对垃圾进行挤压,随后滑板油缸收回,带动滑板在滑槽内上行,将垃圾压入箱体,经反复循环,将垃圾压实压满。故压缩机构对滑板的动、静态性能具有较高的设计要求。
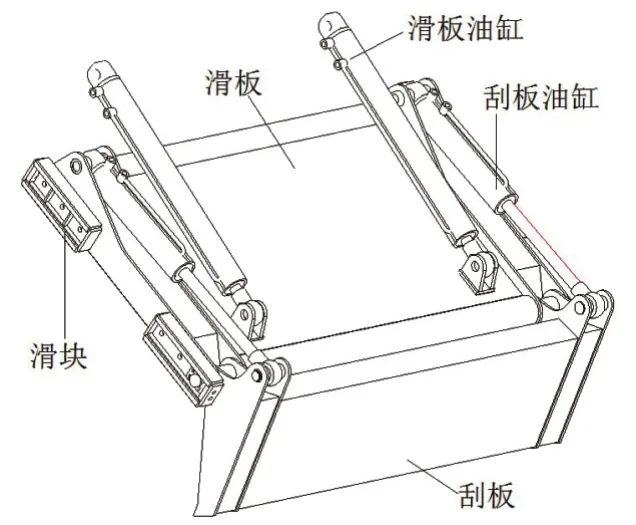
图1 压缩机构
2.2 建立滑板有限元网格模型
利用ProE软件建立滑板三维数学模型,由于滑板是由不同厚度的钢板焊接而成,内部布置有纵横交错的加强筋,其结构比较复杂,且含有许多细小的倒角、圆角、工艺孔等[3]。如果不对模型做适当简化,在网格划分过程中极易产生畸变网格,影响计算精度和时间。故对滑板作如下处理:a. 忽略细小的倒角、圆角;b. 去除对结构无影响的工艺孔[4]。
简化处理后,利用ProE软件可与有限元分析软件无缝对接的功能将模型导入到ANSYS Workbench中,并赋予相应的材料属性,设置泊松比为0.28,弹性模量为210 GPa,选择混合网格划分,最终得到滑板的有限元网格模型,节点数为130 207,单元数为45 146,如图2所示。

图2 滑板有限元网格模型
2.3 滑板载荷确定
滑板的受力分析示意图如图3所示,在工作过程中受到滑板油缸的推力F滑板缸,刮板油缸的推力F刮板缸,滑槽对滑板的支撑力N1、 N2,滑行过程中所受的摩擦力f1、 f2,以及自身的重力G。当滑板油缸和刮板油缸均达到溢流时,此时滑板所受的力最大,即极限工况。为了便于计算,将压缩机构整体进行受力分析,并列如下平衡方程[5]:
2F滑板缸=(N1+ N2)μ+Gsinα+F垃圾cos(β-90°)+2F刮板缸
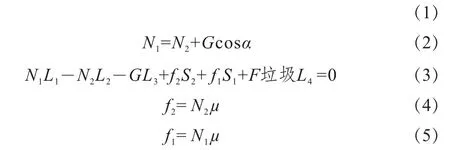
式中,α为滑板的倾斜角;L1、 L2为上、下滑块中心与O1在水平方向的距离;L3为压缩机构质心与O1的距离;L4为垃圾的作用力与O2的距离;S1、 S2为上、下滑块中心与O1在竖直方向的距离;μ为摩擦系数,取μ=0.3。
把相关参数带入式(1)~(5),计算可得:F刮板缸=68 507 N; F滑板缸=92 775 N;N1=85 995 N;N2=89 767 N; f1=25 798 N;f2=26 930 N。

图3 滑板受力分析示意图
3 滑板静力学分析
建立好滑板有限元网格模型后,在滑板上限制3个转动自由度和2个平动自由度,即滑板只能在滑槽方向上滑动,以此来模拟滑板的实际工况[6];将滑板在极限工况下的载荷加载在滑板上,利用ANSYS Workbench对滑板进行静力学分析,求得滑板位移、应力云图,如图4、5所示。

图4 滑板位移云图

图5 滑板应力云图
由图4、5分析结果可知,滑板在压缩垃圾的极限工况下,产生的最大位移量为1.8401 mm,位于滑板的中间部位;最大应力值为223.42 MPa,位于滑板油缸支座焊接处,小于Q235A材料的屈服极限235 MPa,但滑板在反复疲劳作用的情况下,有可能会导致油缸支座断裂,故有必要提高其强度和刚度。
4 滑板的模态分析
模态分析是检验机械结构动态性能的重要方法,由于低阶模态频率和振型对滑板动态性能的影响更大,因此本文提取滑板的前三阶模态参数进行分析[7],通过计算,滑板的前3阶模态频率和振型如图6(a)~(c)所示。
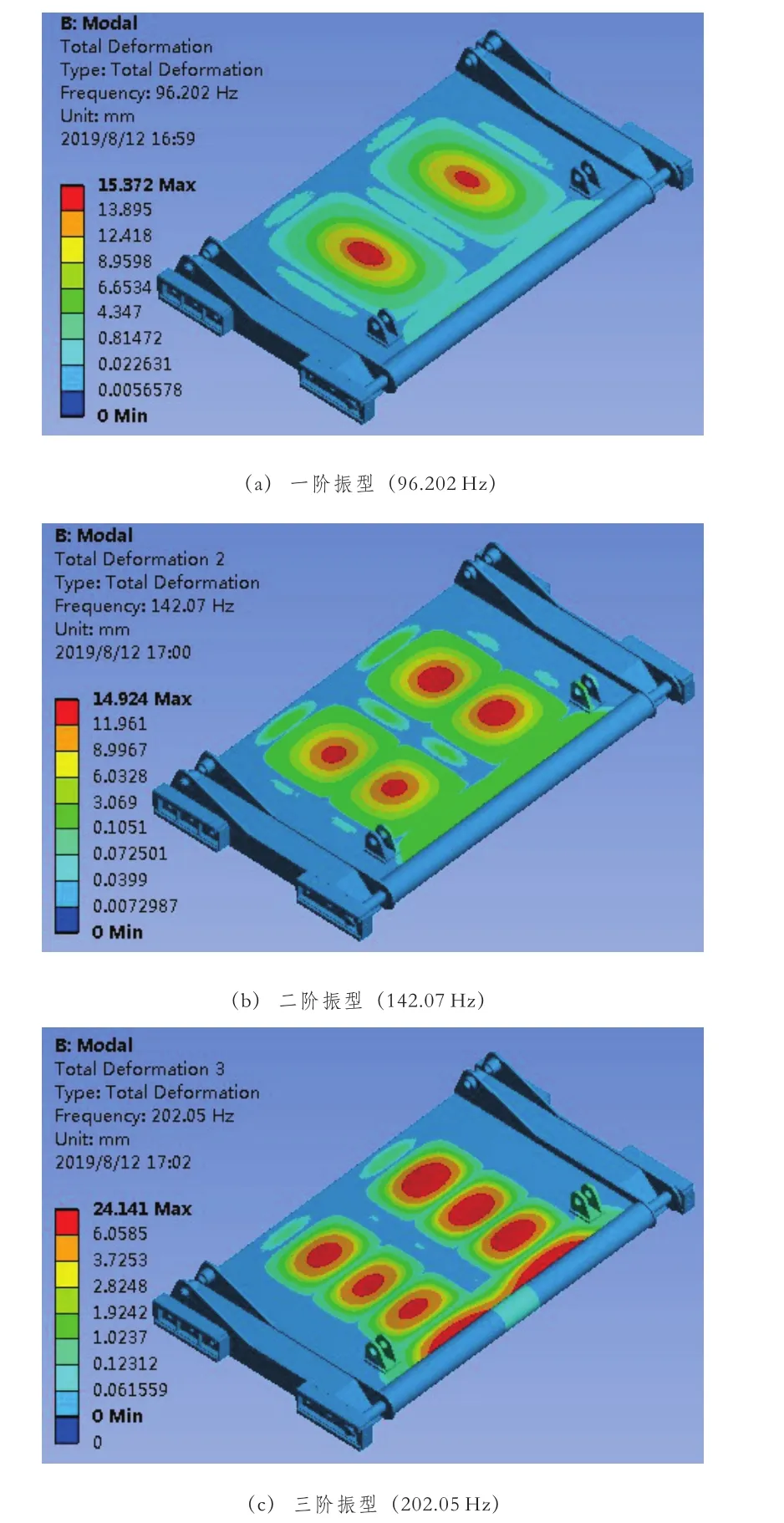
图6 滑板前三阶模态振型
由图6(a)~(c)可知,滑板的前3阶模态频率分别为96.202 Hz、142.07 Hz、202.05 Hz,均大于50 Hz,但滑板的振型在第三阶的时候,于中前部出现摆动和扭转的复合振型,说明在滑板的中前部是相对薄弱的环节,可通过优化滑板的结构和尺寸来提高滑板的动态性能。
5 滑板的尺寸优化
滑板尺寸优化的主要目的是提高刚度、强度、模态频率的前提下对滑板进行减重;灵敏度分析可很好地判断设计变量对目标函数(质量、应力、变形、模态频率)的影响[8]。从而对影响较大的尺寸进行优化取值,刷选最优方案。
5.1 优化尺寸参数的灵敏度分析
滑板框架主要由左右滑板座、2根横梁及3根纵梁所组成,根据动、静态分析结果和滑板的结构特点,可对滑板座壁厚、加强梁和底板厚度进行尺寸优化[9],优化尺寸如图7所示,初始值和变量的变化范围如表1所示。其中,P1为滑板座的壁厚,P2为纵梁的厚度,P3为后横梁的厚度,P4为底板厚度,P5为前横梁的厚度。
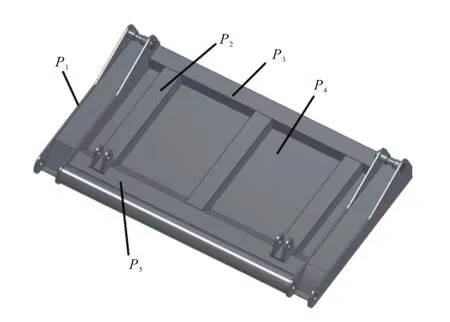
图7 滑板优化尺寸
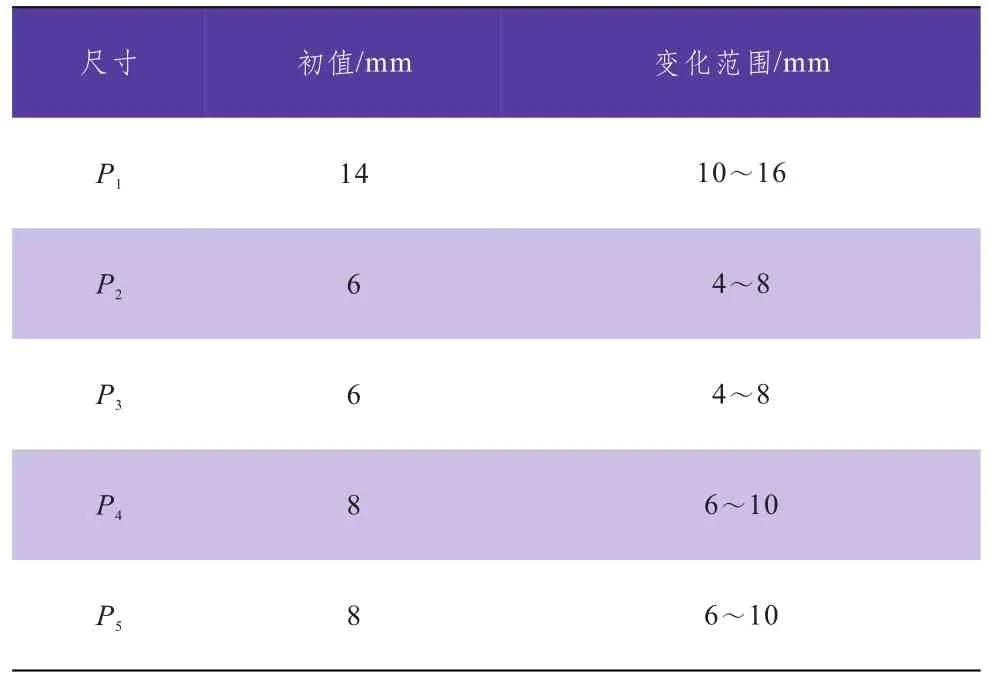
表1 设计尺寸的初值与优化区间
设置好滑板优化尺寸和变量的变化范围后,在ANSYS Workbench软件中进行灵敏度分析,检验它们对质量、位移和模态频率的影响程度,分析结果如图8(a)~(c)所示。
从图8设计变量灵敏度分析结果可知,滑板座壁厚P1、纵向加强梁厚度P2、底板厚度P4对质量、位移以及模态频率的影响最大,故应重点优化;后横向加强梁厚度P3对位移的影响较小,但对质量、模态参数的影响较大,亦可作为优化对象,前横梁厚度P5对质量影响最小,但对位移、模态频率较大的影响,故保留这个优化尺寸。
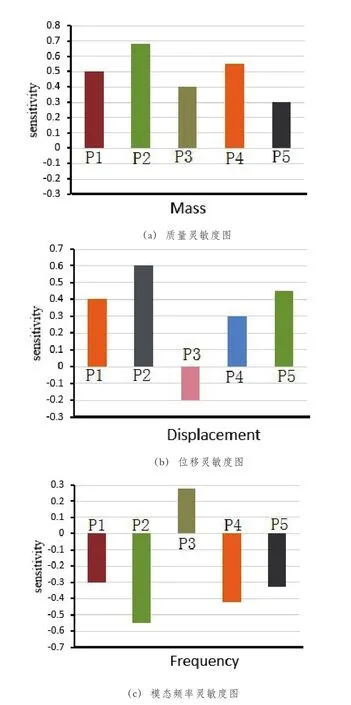
图8 设计变量灵敏度分析图
5.2 滑板尺寸优化结果及分析
由于滑板尺寸优化的主要目的是提高刚度、强度、模态频率的前提下对滑板进行减重,因此在ANSYS Workbench软件中需对目标函数设置相应的优先级,将滑板的位移设置为“High”,模态频率设置为“Default”,质量设置为“Lower”,通过迭代计算,基于优先级的高低对设计变量自动刷选出最优方案,并进行圆整,如表2所示[10]。
根据优化结果重新建立滑板的有限元模型,并在相同的极限工况下对刮板进行静力学和模态分析,滑板优化后的位移云图和一阶振型如图9、10所示,滑板优化前后对比分析如表3所示。
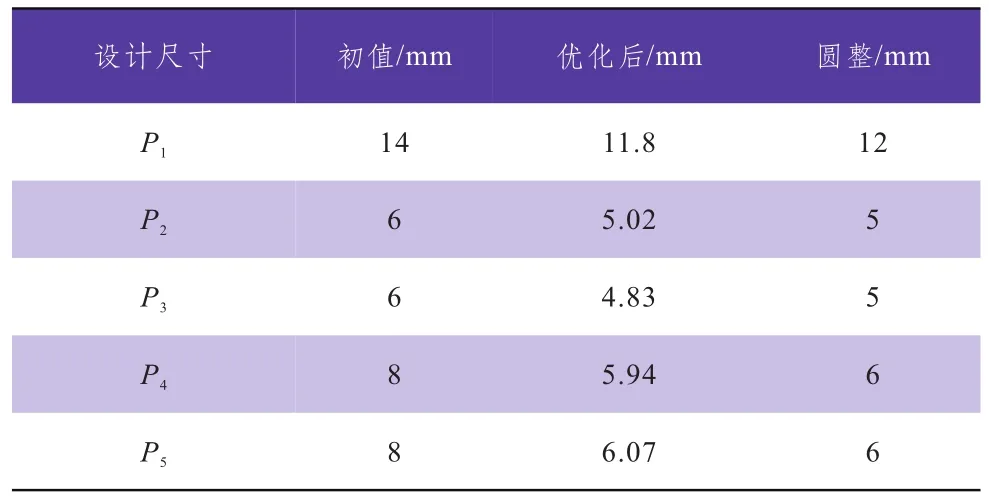
表2 设计尺寸优化前后比较

图9 滑板优化后位移云图

图10 滑板优化后一阶振型(113.26 HZ)
由滑板优化前后对比表可知,滑板减重达32 kg(11%),最大变形减小了6%,应力减小了4.2%,静态性能得到明显提升;在动态性能方面,滑板的前3阶模态频率均有不同程度的提高,尤其是一阶模态频率,提高了17.7%,总体来说,在提高滑板动、静态性能的前提下,实现了滑板的减重。
滑板经有限元分析及优化后,不仅提高了其性能,同时也降低了制造成本,缩短了产品的研发周期,每台车降低成本约32 kg×6.3元/kg=201.6元,按年产量1 000台计算,企业每年可降低生产成本约20.16万元。
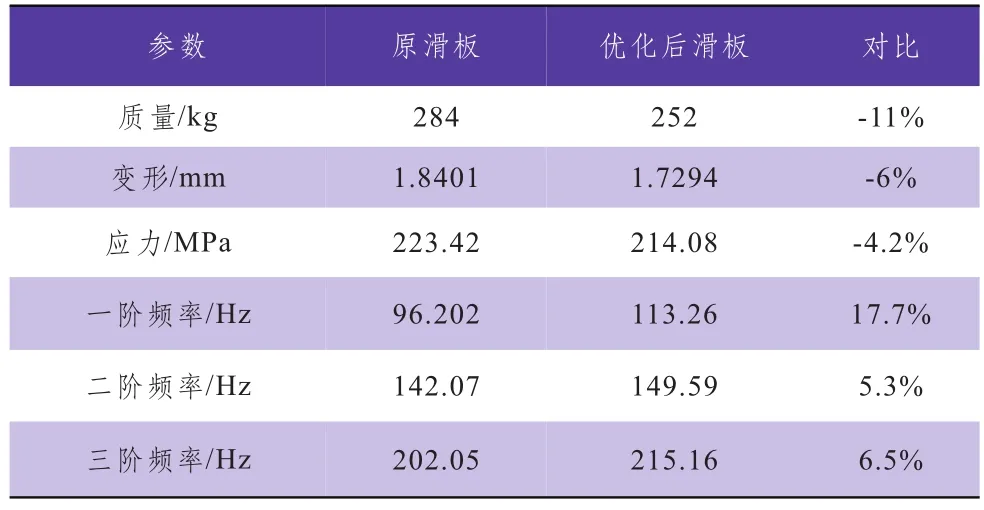
表3 滑板优化前后对比
6 结语
a. 由于垃圾成分不同,滑板的受力性质复杂且难以确定,本文利用刮板、滑板作为一个整体进行受力分析,较好地解决了有限元模型中载荷加载和边界条件设定的问题;
b. 通过对滑板的动、静态分析及灵敏度分析,可直观地反映滑板的动静态性能和可优化空间,为滑板的优化设计提供思路;
c. 通过设定滑板关键尺寸为设计变量,应变、质量为设计目标,对滑板进行多目标尺寸优化,滑板的刚度提高了6%,减重达11%,前3阶模态频率均有不同程度的提高;运用此方法,每年可节约滑板制作成本约20.16万元,并可复制推广到其他零部件,为整车的优化提供思路。
