运行速度对驮背运输安全性影响的仿真分析
2020-04-28林武冯仁锦张皓王凯
林武 冯仁锦 张皓 王凯
眉山中车物流装备有限公司 四川眉山 620020
1 前言
驮背运输是多式联运模式的一种,它结合了公路运输与铁路运输的优点,将原有货物单一的长途汽车运输方式变为公路铁路联合运输方式,通过货运车辆或半挂车承载货物后自行驶入或吊装至专用铁路运输车辆,再通过铁路完成长途运输,到达目标地点后,汽车自行开下或吊离铁路专用车辆并驶往最终目的地的一种快捷运输模式。驮背运输模式如图1所示。
目前国内外学者对于轨道车辆的运行安全性方面做了大量的动力学研究。国外方面,HansTrue等人探讨了轨道车辆系统中的一些非线性情况,并提出了轨道车辆非线性临界速度的基本算法。Schupp利用SIMPACK软件并通过延续算法,研究了复杂轨道车辆系统相关的稳定性问题。国内学者在该轨道车辆运行安全领域内也做了大量的研究。罗仁等通过建立在三种编组条件下列车的纵向-横向-垂向耦合模型,对列车车组中每辆车的线性与非线性运行稳定性进行了仿真研究。赵洪伦等人深入研究了众多优化方法,通过纵横向定位刚度的变化以及对于其临界速度的分析提高了列车的运行安全性。
图1 驮背运输模式
以上研究均针对的是普通铁路客运和货运车辆,并未针对驮背运输车辆进行专门研究。目前驮背运输在我国尚处于起步阶段,有关驮背运输车辆的仿真研究相对较少。本文讨论的驮背运输车单车车体长度为19.32 m,转向架中心距为17 m。与计算车辆相比,车辆定距较小。本文应用Simpack软件及与轨道车辆仿真相关的理论,对铁路驮背运输车辆系统进行仿真,分析得出铁路驮背运输车辆运行的安全速度。
2 驮背运输车辆仿真
2.1 仿真样车的选取
本仿真选用的是某型铁路驮背运输车,动力学参数如表1所示,单车长度约为19.32 m,车辆承载面长度约为15 m,最大载重不超过49 t,如图2所示。
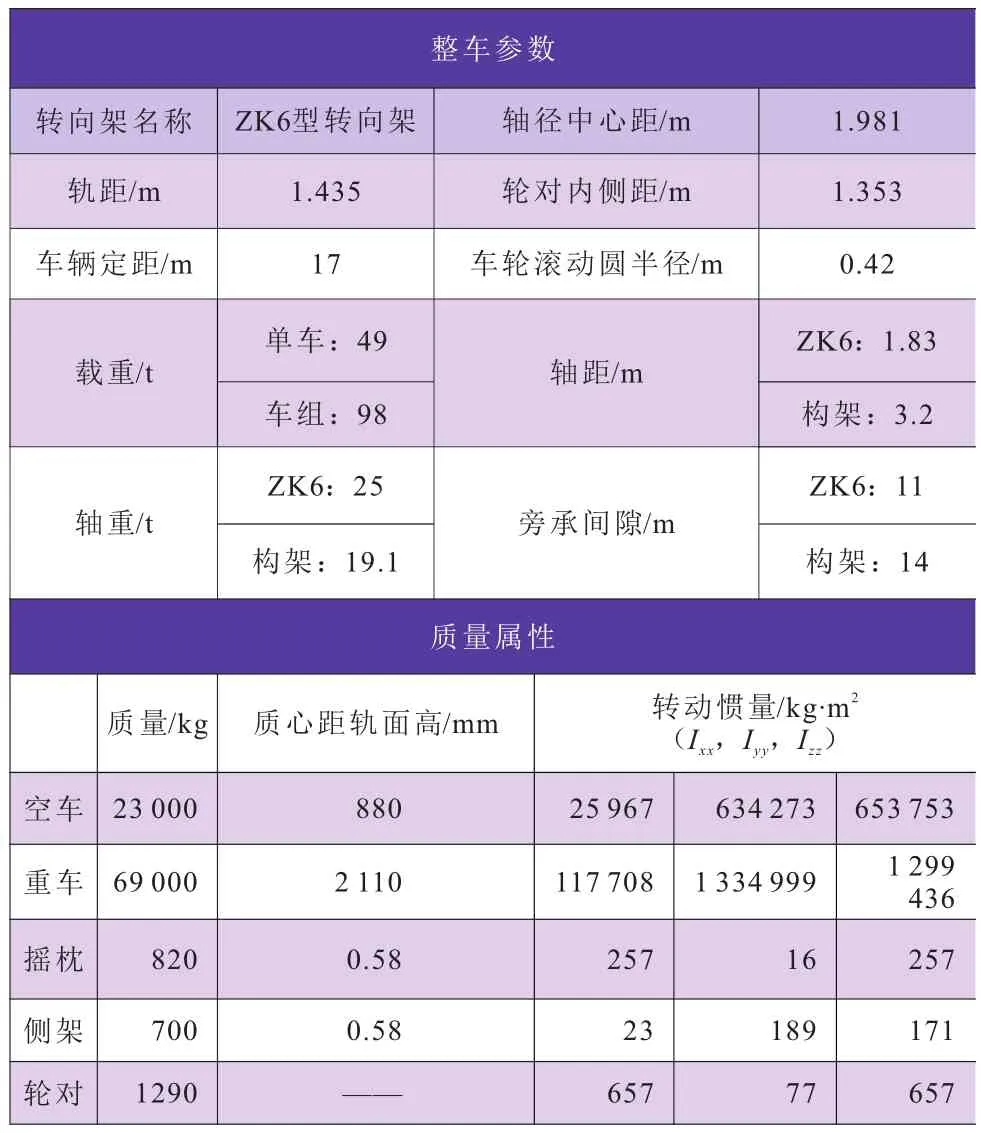
表1 铁路驮背运输车辆整车参数表

图2 仿真用驮背运输车辆
2.2 模型建立及简化
在Simpack软件的rail_track模块中依次建立轮对模型、侧架模型、承载鞍模型、虚车体模型、摇枕模型,ZK6转向架模型由以上几个子模型组成,接下来在此模块下建立车体模型,车体模型和前后转向架模型装配构成了铁路驮背车辆的总体模型。
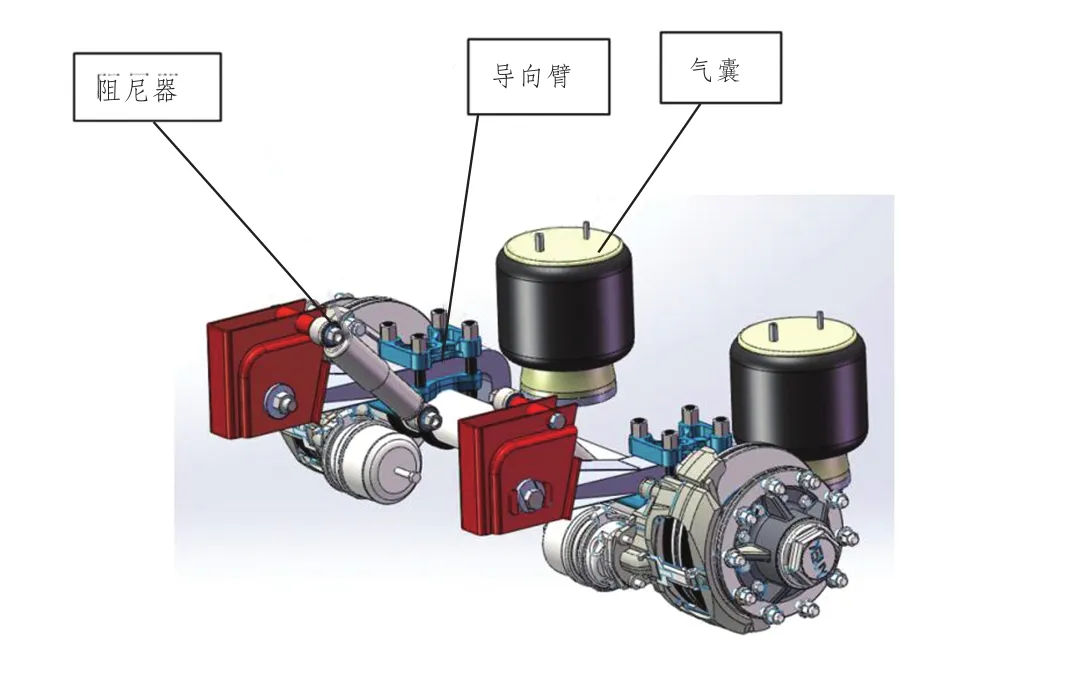
图3 半挂车空气悬挂系统
运输的半挂车空气悬挂系统如图3所示,参考UIC596-5铁路货车运送公路车辆标准,空气悬架气囊在铁路运输过程中应保持无气状态,这是因为半挂车上铁路驮背车辆后,就切断了供气系统,在长时间的运输过程中,由于铁路驮背车辆颠簸运行,气囊里的气体在半挂车高度控制阀作用下一点点地排出,会增加运输过程中的不稳定性。放气后半挂车支撑在气囊缓冲块上,缓冲块加上导向臂和阻尼器就是一个刚性支撑,故半挂车可简化为一个质量块模型,整体模型如图4所示。
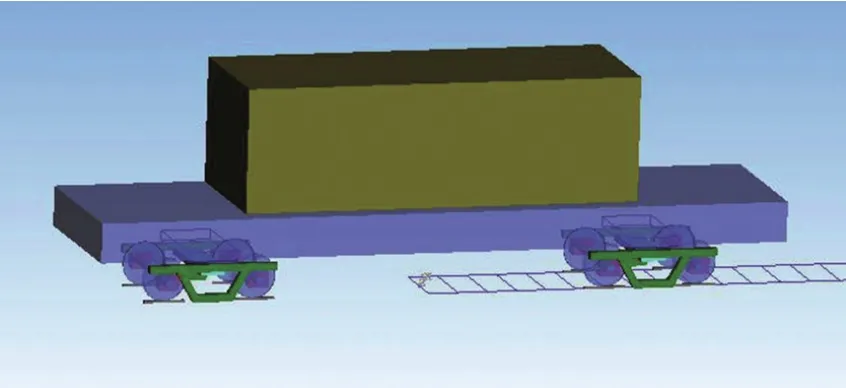
图4 Simpack铁路驮背运输车辆模型
2.3 施加约束
通过表2所示的ZK6转向架的具体铰接方式进行约束施加,并定义模型中存在的二系力,车辆系统总体拓扑关系如图5所示。
a.定义一系力作用在铁路驮背运输车辆承载鞍和侧架之间,在铁路驮背运输车辆承载鞍和侧架之间建立一系力标记点,所述标记点即为铰接点,将车辆一系悬挂的实际刚度值和阻尼值输入到Simpack软件中定义完成一系力。承载鞍与侧架之间通过Simpack软件中的2号铰接形式铰接;
b.定义二系力作用在铁路驮背运输车辆摇枕和侧架之间,在铁路驮背运输车辆摇枕与侧架之间建立二系力标记点,所述标记点即为铰接点,将二系悬挂实际刚度值和阻尼值输入到Simpack软件中定义完成二系力。摇枕与侧架之间通过Simpack软件中的25号铰接形式铰接。
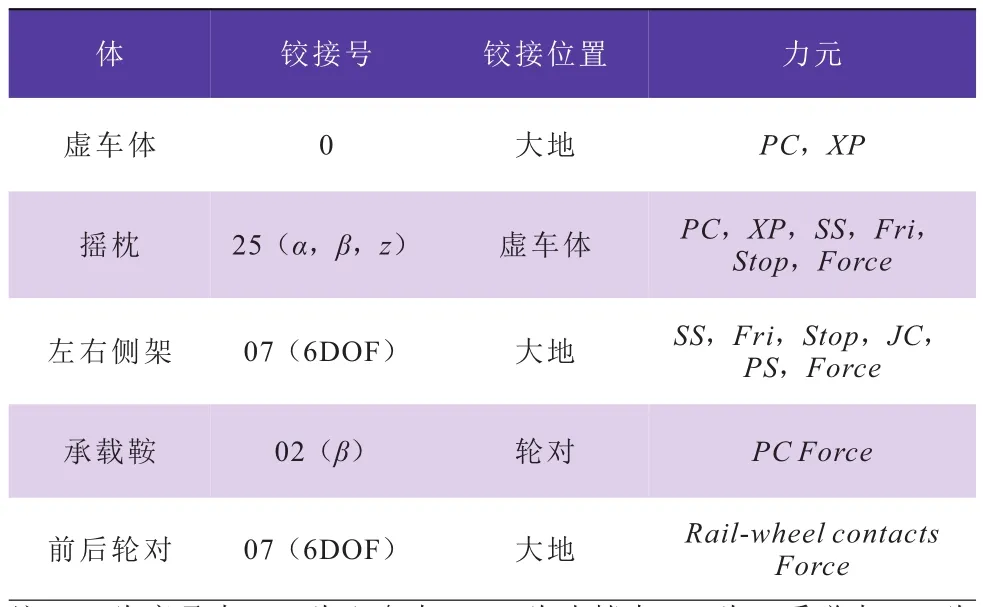
表2 ZK6转向架的具体铰接方式
图5 铁路驮背运输系统总体拓扑图
2.4 仿真条件设定
当车辆系统受到一个初始激励后,分析车辆在不同的运行速度下轮对横移量随时间的变化情况,如收敛,则车辆处于稳定状态,如图6所示;如发散,则车辆处于失稳状态,如图7所示;如既不收敛,也不发散,则车辆处于临界状态,如图8所示,此时相对应的车辆运行速度称为车辆的临界速度。
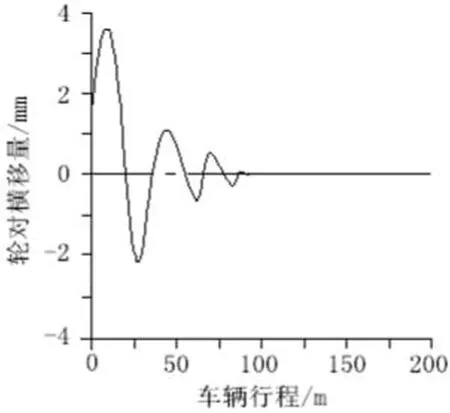
图6 稳定状态下轮对横移量随行程变化曲线

图7 失稳状态下轮对横移量随行程变化曲线
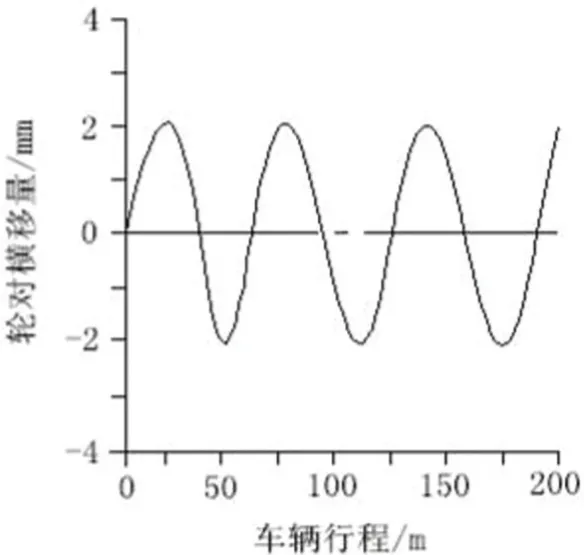
图8 临界状态下轮对横移量随行程变化曲线
在Simpack软件中对轨道施加激励前,需要先定义输入的函数列,新建名称为“Track-related”和“Rail-related”的函数列,分别选择T R E激励文件“binary_track_excit_tre”和“binary_rail_excit_tre”,定义完成横向、垂向、侧滚、轨距、左右横向和左右垂向8种不平顺条件输入函数,其中横向不平顺函数图如图9所示。
在Simpack软件中新建一个横向的轨道不平顺条件,名称为“Lat”,在Type中选择Distance Domain(空间域)里面的“109:From Input Function(Adv)”,因为轨道不平顺一般都是空间域的,如果选择时域或者频域的激励是施加不到线路上去的。在输入激励功能项中选择上一步建立的输入函数列“I_Lateral”,定义完成轨道横向激励,如图10所示。用同样的方法定义其他7种不平顺条件。将定义好的激励施加与轨道不平顺条件中,激励开始位置、激励平滑长度和激励终止位置分别为50m、5m、100m,如图11所示。接下来进行临界速度分析。使用单次积分法计算非线性临界速度,线路是有50 m激励的直线,然后让车辆以一定的速度通过,看左右轮对的横移量,按2.4章节所述的评价原理进行判断,如果收敛,增大此时的仿真速度,如果出现等幅震荡,那么可以取两次仿真速度的中间值,再进行计算,直到找到时速为akm/h,那么轮对横移量是稳定状态,而在(a+1)km/h为临界状态,那么(a+1)km/h为临界速度。
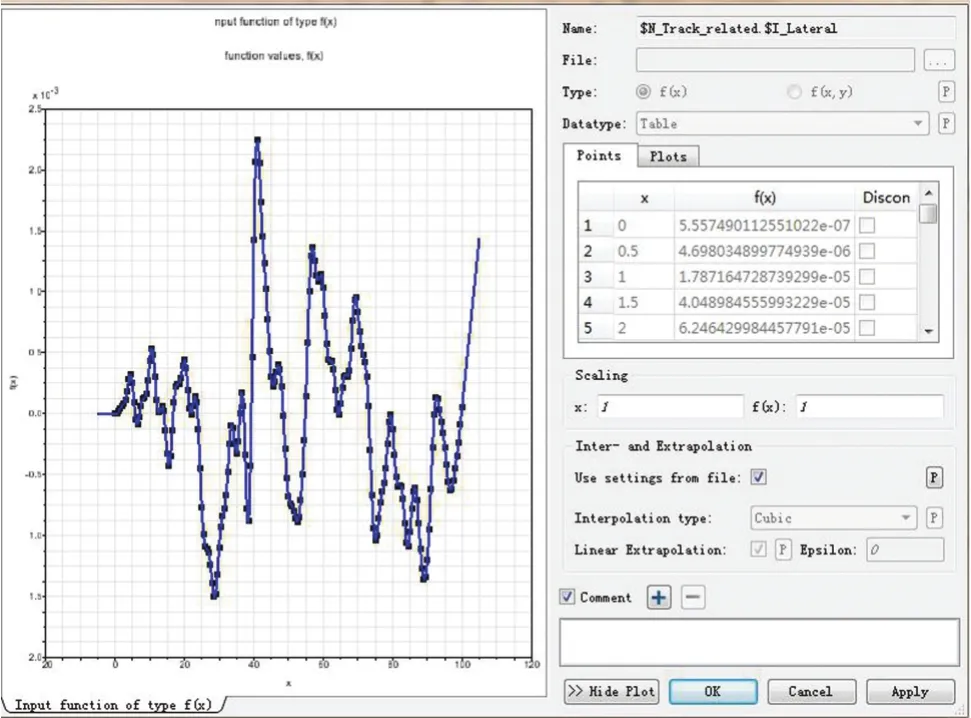
图9 横向不平顺函数定义
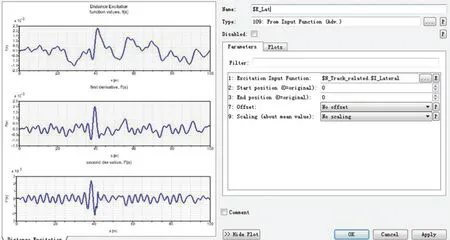
图10 定义横向激励
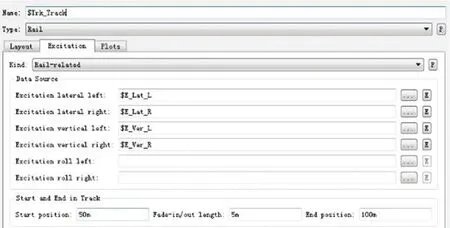
图11 施加轨道不平顺条件
初始仿真速度设置为100 km/h,仿真时间设置为15 s,采样频率设置为100 Hz,进行离线积分,得出轮对横移量随时间的变化曲线。逐渐增加仿真速度,进行离线积分,得出轮对横移量随时间的变化曲线。
3 仿真结果分析
仿真速度设置为100 km/h时,轮对横移量随时间的变化曲线如图12所示。
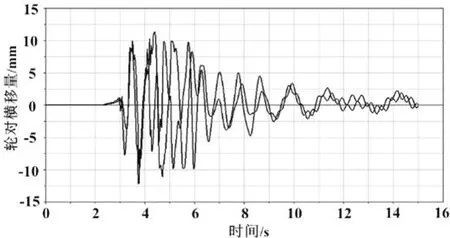
图12 100 km/h时轮对横移量随时间变化曲线
由图12可以看出:铁路驮背运输车在仿真进行4 s后速度达到100 km/h,此时轮对横移量随着速度的增大而增加,从图中可以看出最大横移量数值约为12 mm,之后车辆仍然安全运行,在6 ~15 s内车辆处于恒定速度状态,轮对横移量也逐渐有规律的减小,此时车辆进入稳定状态,说明100 km/h为安全运行速度。
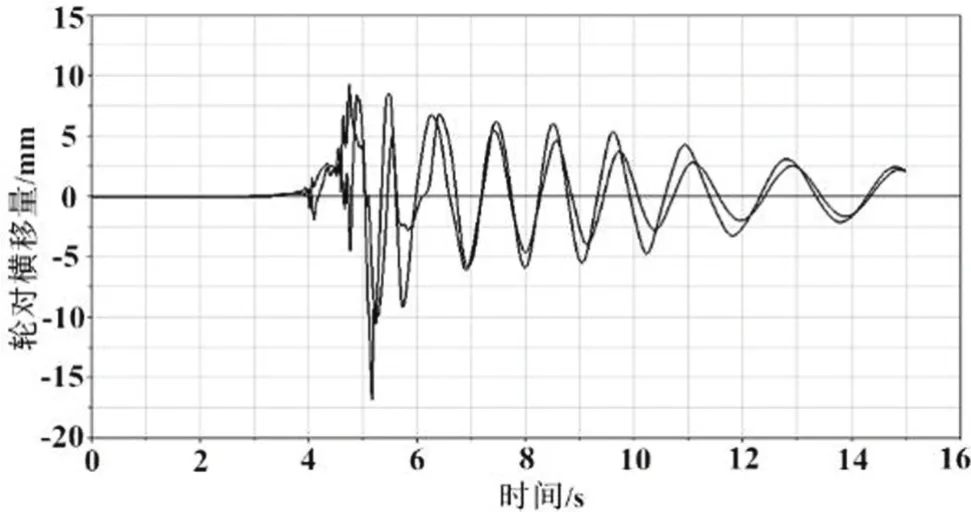
图13 110 km/h时轮对横移量随时间变化曲线
由图13、14可以看出:随着仿真速度设定值增大,车辆进入稳定速度前的4~6 s内,轮对横移量数值较大,最大横移量约为17 mm,仍然处于安全范围内,6 s之后车辆运行速度稳定,横移量逐渐呈规律性减小,说明车辆仍然处于安全运行速度下的稳定状态。6~15 s时,轮对横移量曲线随时间的变化越来越趋于平稳,证明此时车辆运行速度符合安全性要求。
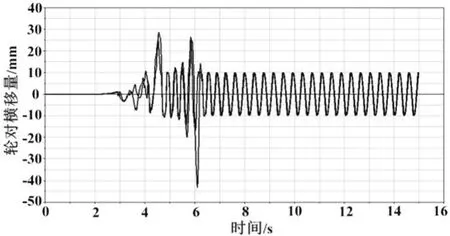
图14 119 km/h时轮对横移量随时间变化曲线

图15 120 km/h时轮对横移量随时间变化曲线
由图15可以看出:在速度处于恒定状态以前,最大横移时间出现在6 s左右,最大横移量为43 mm左右,6 s后当速度处于恒定状态时,轮对横移量也处于恒定状态,根据图6所示的原理图,速度为120 km/h时,6 s后的轮对横移量随时间变化曲线既不收敛也不发散,说明此时的速度为临界速度。
由图16所示,将仿真速度设置为121 km/h时,速度在进入稳定状态后,轮对横移量随时间变化曲线呈发散状态,最大横移时间出现在仿真时间的15 s左右,最大横移量约为43 mm处,之后根据图线呈现的规律可看出,轮对横移量将随时间逐渐增大,直至轮对横移量超出安全横移范围,车辆失稳。
由上述仿真结果总结:在仿真速度120 km/h前轮对横移量随时间变化逐渐降低,说明车辆系统逐渐趋于稳定状态,当速度达到120 km/h时,轮对横移量随时间变化保持一个不变的值,图线既不现收敛也不发散,说明此时车辆系统处于临界状态,当速度大于120 km/h时,轮对横移量曲线波峰开始逐渐增大趋于发散状态,说明此时车辆系统正趋于失稳状态。
4 结语
a.通过Simpack软件对铁路驮背运输车辆系统进行模拟和仿真,可通过软件自带的离线积分功能快速地计算出所需要的各种数据,包括本文所得到的运行速度相关数据,也可得到运行过程中车辆结构内产生的力的大小,为实际的车辆系统试验提供了一定的依据。
b.通过单次积分法计算运行速度,再通过轮对横移结果图判定车辆系统的临界速度,仿真得出该铁路驮背运输车辆系统的最大运行速度为120 km/h,对于该车辆系统的安全运输具有指导性作用。
c.随着仿真软件的逐步升级,仿真技术不断发展,对于车辆仿真的精确度要求越来越高,仿真结果与实际实验结果的相符程度决定了对于仿真结果的一系列应用,所以对于该铁路驮背运输系统的实际动力学试验,是接下来要做的工作。
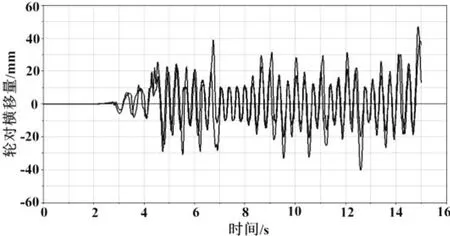
图16 121 km/h时轮对横移量随时间变化曲线
