优化设计，提升推理能力

姚园

摘要：推理能力是数学学习十大核心素养之一，也是学生数学学习必备的能力之一。本文从日常教学中的问题出发，通过设计和实践教学过程，得出了几点经验，以期培养学生的推理能力，提高小学数学教学的有效性。

关键词：小学数学   三角形   三边关系   推理能力

一、缘起：寻找瓶颈，落实推理

《三角形三边关系》属于空间与图形范畴的内容，它建立在学生初步认识角、认识三角形的基础上。要想提高《三角形三边关系》的教学效率，教师必须有效解决以下四个问题：①给学生一些线段，学生能从中选取合适的线段围成三角形吗？②围成或围不成三角形的关键在哪里？教师提供的材料会影响学生操作或者结论的产生吗？③这些问题的思考是停留在操作层面，还是在操作中需要学生具备一定的推理能力？④如何在教学环节落实发展学生推理能力的目标？

基于以上四个问题，笔者设计和实践了《三角形三边关系》的问题情境与练习，并论述了实践后的反思与思考。

二、践行：追根涟源，落地抓手

笔者对《三角形三边关系》的教学进行了如下设计与实践：

1.复习引入，埋下推理的种子

笔者提出问题：“如图1所示，判断下面哪些图形是三角形，并说明理由？思考是不是任意的三条线段都能围城一个三角形？”

在本环节中，笔者选取了最常见的一种导入方式——复习引入，让学生通过判断图中哪些是三角形，以此明确三角形有三条边，且三角形是一个由三条线段围成的封闭图形，从而让学生复习已有的知识，主动进行思维活动。“是不是任意的三条线段都成围成三角形呢？”这一问题不仅顺势引出了本节课的学习主题，还给学生埋下了推理的种子。

2.关系展开，促进推理能力的发展

学生推理能力的形成是一个缓慢的过程，它必须通过整个数学学习活动才能形成。

（1）情境设计，搭建推理平台

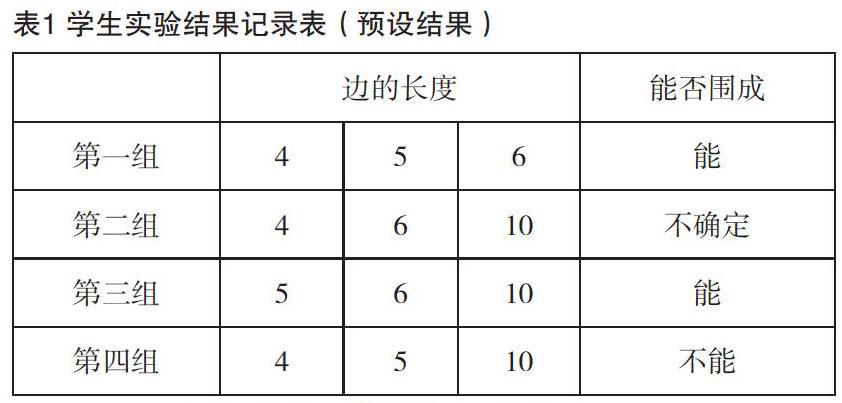
本案例中，笔者为每个学生提供了4根长短不一的小棒，分别为4厘米、5厘米、6厘米、10厘米，让学生任意取3根，开展围三角形的实验，为学生后续的推理搭建平台。同时，笔者还设计了“每次都能围成三角形吗？你有什么发现？”等问题情境，明确告知学生需要做什么，该怎么做。这样一来，学生能在更加自由广阔的空间中合作、探究和发现。除此之外，笔者还提供了4根小棒让学生展开围三角形的实验。一方面，让学生明确三角形是一个由三条边围成的封闭图形，重溫了三角形的特征知识;另一方面，学生通过实验、激疑、观察、合作交流、验证等环节，发现并不是任意的三根小棒都可以围成三角形（如表1所示），三角形的三边具有特定关系。由此可见，问题的设计起到了知识点间承前启后的作用，使得推理有根可寻。

（2）分析特例，提供推理依据

在学生动手实验后，笔者问学生：“第二组确定不能围成三角形吗？”

学生1说：“我把两条边往下压，两条边越来越接近，最后在很低的时候接上了。”

笔者接着问：“那是围成了三角形，还是没有围成三角形呢？”

学生2说：“我反对。一直把两条边往下压，两条边越来越接近，直到最后是三条边重合在了一起，而不是围成三角形。”

学生3说：“这样不能围成三角形，因为4+6=10，最终只能重合。”

笔者最后问：“通过实验，你们得出了什么结论？”

学生齐声回答：“两边之和等于第三边不能围成三角形。”

针对第二组的结论，学生分歧很大，部分学生认为可以围成三角形，部分学生认为不能围成三角形。于是，笔者让学生进行实验并交流，一步步引导他们发现和解决问题。当两根小棒之和等于第三边时，实验呈现的结果不是很明确，所以笔者继续追问学生，使得学生不断在围成与围不成三角形中进行操作与推理，最终得出正确的结论。

笔者继续问学生：“第四组真的不可以围成三角形吗？”

学生1回答：“我把4和5的两条边不断往下压，发现两条边越来越靠近，但是直到平行还是会有一个缺口，所以围不成三角形。”

学生2回答：“4+5=9，两条短边加起来比10小，所以永远不可能围成三角形。”

笔者说：“通过这组实验，你们发现了什么？”

学生3回答：“当两短边之和小于第三边，不能围成三角形。”

这一组的实验结果很一致，学生通过操作后发现：当短的两根小棒之和都不及一根长的小棒时，那么这三根小棒是不可能围成三角形的。在这一环节的交流过程中，学生通过实验、观察和验证，自然而然地得到了结论。

（3）猜测结论，指明推理方向

学生通过分析四组实验的情况，尤其是分析两个反例后，借助前面已有的结论与经验进行有目的地猜测（合情推理），得到一个结论。推理是建立在大胆的猜想之上的，所以笔者鼓励学生通过观察、实验、类比、归纳等方法大胆提出猜想，有助于学生掌握数学知识，学会了探求知识的方法。

（4）验证数据，证明推理结果

最后，笔者问学生：“请你们观察一下，任意两条边之和大于第三条边就能围成三角形吗？”

学生1回答：“这个说法不对，第二组中4+10>6，可是这三根小棒不能围成三角形。”

学生2回答：“是的，第四组中4+10>5，也围不成三角形。”

笔者问：“那么到底什么情况下才可以围成三角形呢？”

学生3回答：“我发现了，只要加上任意两字就可以了。你看第一组中4+5>6，5+6>4，4+6>5。”

笔者问：“你们能得出结论吗？”

学生齐声回答：“任意两边之和大于第三条边才能围成三角形。”

学生4说：“我有补充，只要两条短边的和大于第三边就行了。”

学生从已有的事实出发，发现在围不成三角形的实验中，仍然存在两边之和大于第三边的情况，所以结论其实是不正确。随即，笔者提出质疑：“到底三角形的三边有何关系？”伴随着猜测，学生通过事实数据得到了证实，进一步完善了第一猜测的结论。这样一来，学生用已有实验的结果事实推翻了前一次的猜测结论，然后又大胆进行第二次猜测，再一次得到证实，合情推理与演绎推理完美结合，两者相辅相成。

3.分层练习，助力推理能力的提升

练习不仅能巩固所学知识，还能升华知识。因此，笔者设计了巩固型、拓展型、应用型三个层次的练习。

（1）巩固型

笔者设计了这样一道目：下面四组线段能围成三角形吗？（单位：厘米）

①4，9，5;②8，7，6;③3，10，5;④6，7，10。

通过出示四组数据的线段，笔者让学生判断它们能否摆成三角形，并给出合理的解释，从而简单巩固与应用三角形三边关系的特征，提高学生的推理能力。

（2）拓展型

笔者设计了这样一道题目：已知两条线段的长度分别为4厘米与9厘米。①另有长度分别为5厘米、6厘米、7厘米、13厘米的线段，能与前两条线段组成三角形的线段有哪几條？②第三条线段还可以是哪些长度（取整理米数），它最长是多少厘米？最短是多少厘米？

在解答这道题目时，学生需要逆向思维，所以笔者把问题分为两个小问题，让学生利用已有的知识（三角形任意两边之和大于第三边）进行演绎推理，选取合适的第三条边。在解答第二个小问题时，学生在深刻体会两短边之和大于第三边的规律后，发现要保证围成三角形，除了两边之和要有关系，两边之差也同样存在关系，从而得出三角形中两边之差必定小于第三边的结论。

（3）应用型

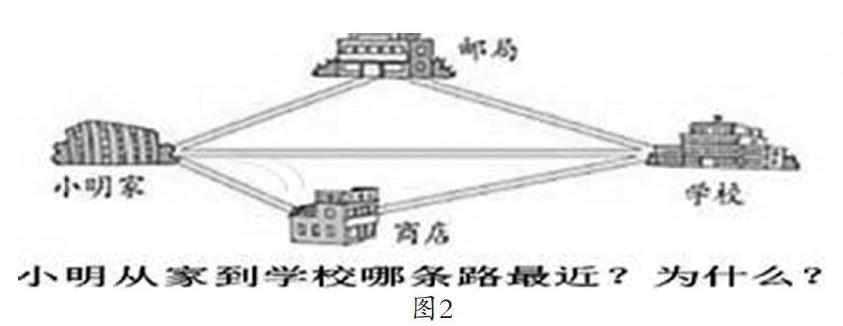
如图2所示，这道练习题的设定，一方面，能让学生认识到数学结论不仅可以解决数学问题，还能解决生活问题，激发学生的学习兴趣，为培养学生推理能力打下良好的基础;另一方面，学生通过已有的知识又推理出了一个新的结论，即两点间直线段最短。

三、启迪：形成策略，提升学力

《小学数学新课程标准》指出：“推理能力的发展应贯穿于整个数学学习过程。”那么，如何培养学生的推理能力呢？

1.还原数学的思考，提供推理平台

“三角形任意两边之和大于第三边”是个事实性结论，学生接受起来十分容易。但他们常常难以洞悉结论背后隐藏的思考，如为什么三角形中任意两边的和会大于第三边。因此在教学中，笔者花费了大量时间让学生经历实验，观察、猜想、证明这些过程，得出“任意两边之和大于第三边就能围成三角形”这个逆命题，从而理解原有的事实性结论。笔者认为，在教学过程中，教师应努力还原数学的思考过程，无论是计算方法的获得、规律公式的应用，还是问题的解决，教师应多提出诸如“为什么”“你是怎么想的”等问题，鼓励学生从数学知识的本质、意义上出发进行推理，以获取方法的总结或结论的成立。

2.外化推理的过程，培养推理能力

简单而言，推理的目的是为了证实结论。但是，在培养学生推理能力的过程中往往存在一些问题。第一，在引领学生推理时，教师重视结论、轻视推理的过程;第二，学生的推理过程比较内隐，教师会忽视学生推理过程是否正确，导致学生的推理能力无法得到真正意义上的提高。因此，教师必须让学生的推理过程外显化。

在教学《三角形三边关系》的过程中，笔者让学生把围三角形的操作结果记录在表中，呈现出操作结果。然后，学生通过观察，以及同学间的相互交流、师生的对话，分析实验数据，并最终获得结论。这样，学生能学会用语言描述数学知识的形成过程，有利于学生的思维外化，也有利于教师有针对性地引导学生的推理过程、方法等，有效培养学生的推理能力。

3.积累活动的经验，提升推理能力

经验是个性化的产物，它看不见，也摸不着，但经验的积累离不开个体的亲身经历。在教学过程中，笔者让学生通过实验经历学习过程，使学生体会了探究新知识的乐趣，积累了数学活动的经验，提升了数学推理能力，这也是实验 的教学价值。因此，小学数学教师要让学生多经历“猜想—证明”的问题探究过程。值得注意的是，在教学过程中，教师要处理好自身的进退关系，关注学生的亲身经历，鼓励学生用合情推理进行大胆推测，最后发现结论，再用演绎推理证实结论，完成整个推理过程，进而提高学生的推理能力。

参考文献：

[1]教育部.数学新课程标准[M].北京：北京师范大学出版社，2011.

[2]刘加霞.探究性教学要选择“好素材”[J].教育大观，2011，（23）.

（作者单位：杭州市卖鱼桥小学）