自由节曲线非圆齿轮驱动差速泵设计与性能试验

徐高欢 谢荣盛 孙培峰 赵华成

(浙江水利水电学院机械与汽车工程学院， 杭州 310018)

0 引言

差速泵是利用差速机构驱动的新型容积泵，可以取代农业常用的容积泵，如大型植保机械的柱塞泵、隔膜泵等[1-4]，满足农业低脉动率和大排量的要求，提高植保机械施药效果[5-8]。差速泵主要通过不等速机构驱动相邻叶轮周期性差速转动，实现容积腔密闭空间的周期性变化和液体的周向转移，实现输送液体的功能[9]。根据叶片的驱动方式不同，目前差速泵主要有转动导杆齿轮式差速泵[10]、万向节齿轮机构驱动差速泵[11]、非圆齿轮驱动差速泵[12-13]3种类型。其中，非圆齿轮驱动机构是差速泵的主要驱动形式，而傅里叶非圆齿轮驱动机构为优选驱动机构[14-15]。由于傅里叶节曲线的调整参数为8个，局部优化能力有限，因此傅里叶非圆齿轮驱动差速泵的脉动率、不根切最大模数等性能还存在优化空间。在变性高阶比傅里叶非圆齿轮驱动的六叶片差速泵研究中，本课题组通过增加变性系数提升傅里叶节曲线局部优化能力，改善了差速泵性能[13]，但是较大变性系数会导致排量和不根切最大模数变小，变性系数可调范围较小，具有局限性。经研究发现，非圆齿轮节曲线利用k次B样条曲线设计可进一步改善局部调控能力。本文以结构较为简单的四叶片差速泵驱动的最优傅里叶节曲线为基础，建立数学计算模型，编写性能计算软件，通过计算和试验分析，设计k次B样条曲线控制顶点，再微调控制顶点生成自由节曲线，以期改善非圆齿轮驱动差速泵的性能。

1 自由节曲线非圆齿轮驱动的差速泵结构和原理

1.1 基本结构和工作原理

驱动差速泵的非圆齿轮利用k次B样条曲线设计节曲线，该节曲线定义为自由节曲线，通过控制点确定控制多边形，最后确定节曲线型值点，调整控制点可以任意控制节曲线形状。控制点可以对节曲线进行任意位置形状的调整，使节曲线具有任意的局部变形能力[16-21]，如图1所示。自由节曲线非圆齿轮驱动的差速泵主要由自由节曲线非圆齿轮副和滑动的差速叶轮组成，如图2所示。

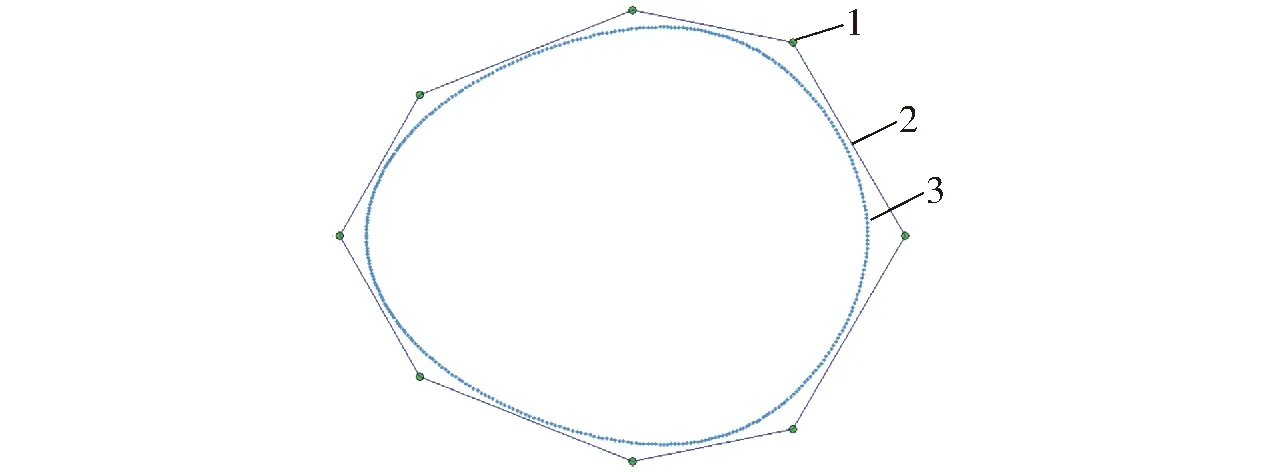
图1 控制点与自由节曲线Fig.1 Control point and free pitch curve1.控制点 2.控制多边形 3.自由节曲线

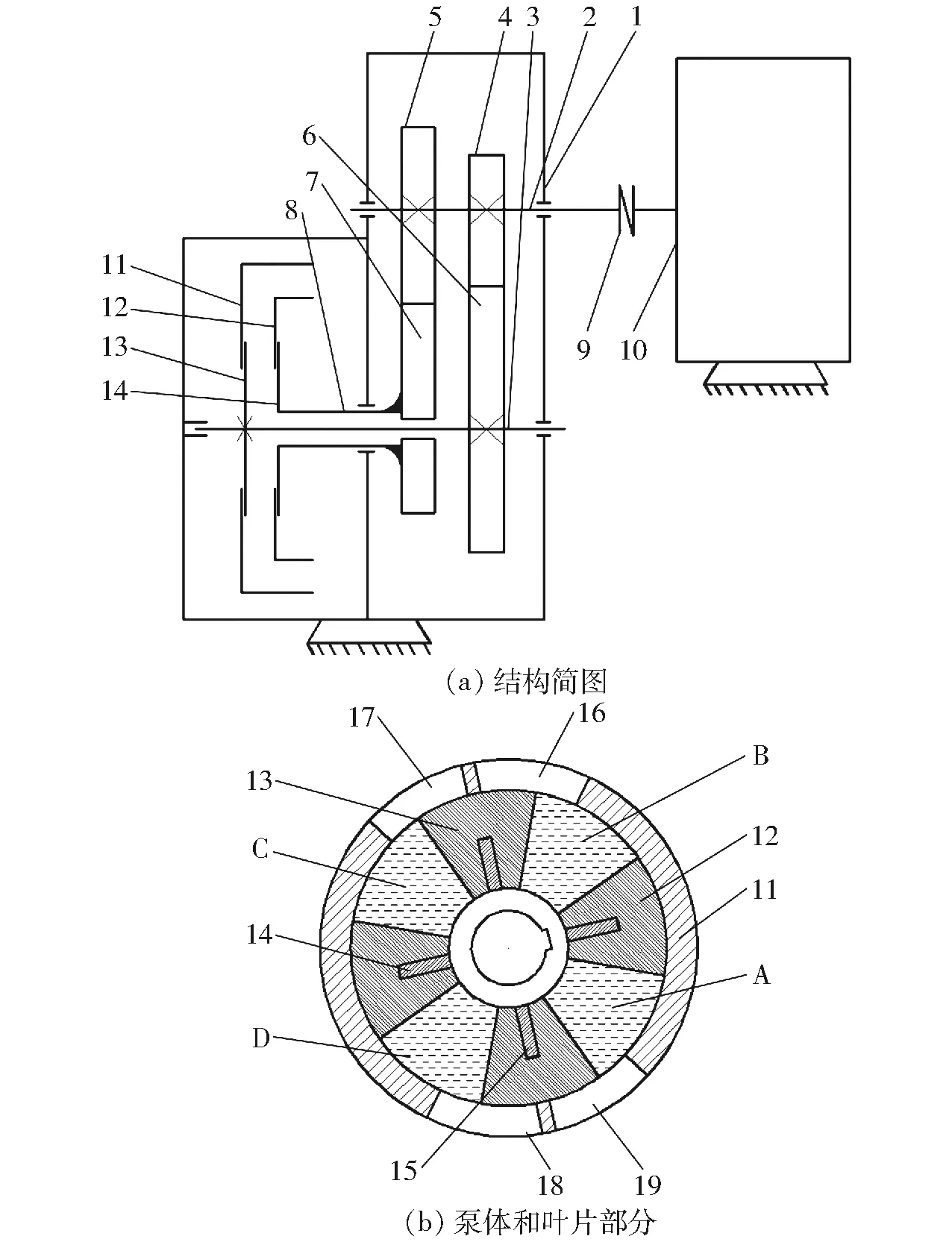
图2 自由节曲线非圆齿轮驱动的差速泵Fig.2 Differential pump driven by non-circular gear with free pitch curve1.驱动齿轮箱 2.输入轴 3.输出轴 4.第一自由节曲线非圆齿轮 5.第二自由节曲线非圆齿轮 6.第一共轭自由节曲线非圆齿轮 7.第二共轭自由节曲线非圆齿轮 8.轴套 9.联轴器 10.电机 11.泵壳 12.第一排液口 13.第一吸液口 14.第二排液口 15.第二吸液口 16.第一滑动叶轮 17.第二滑动叶轮 18.第一滑轨 19.第二滑轨

以自由节曲线非圆齿轮驱动的四叶片差速泵为例，第一、第二自由节曲线非圆齿轮同轴相位差180°安装，自由节曲线参数相同，随电机作匀速转动，分别驱动第一、第二共轭非圆齿轮，带动相连接的第一叶轮和第二叶轮作周期性差动周转，A、C腔处于第一、二吸液口时，第一叶轮转速快于第二叶轮，A、C腔容积增大吸入液体；此时B、D腔容积减小，分别从第一、二排液口排出液体；共轭非圆齿轮带动叶轮周转，驱动B、D腔内液体逆时针转移，分别转到第一、二排液口，根据设计的运动规律，实现容积的增加和缩小，上述运动不断重复，实现容积泵功能[22-23]。另外该差速泵叶轮为滑动叶片设计，第一滑动叶轮和第一滑轨移动副连接，第二滑动叶轮和第二滑轨移动副连接，第一滑轨、第二滑轨分别固定在输出轴和轴套上，第一滑动叶轮和第二滑动叶轮均对称设置有两片滑动叶片，沿圆周方向，第一滑动叶轮的叶片与第二滑动叶轮的叶片相间设置，所有叶片可沿着滑轨滑动。可以防止由于泵外壳变形卡死，同时可以补偿叶片弧面磨损造成叶片和泵壳缝隙过大，滑动叶片在容积腔短暂困液时，叶片通过向轴心滑动实现短时泄压[23]。

1.2 基本数学模型

利用k次B样条曲线设计自由节曲线，第一自由节曲线表达式为[22-23]

(1)

式中Pi——第i个控制点

ti——第i个参数节点向量

Ni,k(t)——k阶k-1次B样条函数

3阶B样条基函数表达式为

(2)

根据第一自由节曲线表达式，可得第一自由节曲线向径表达式为

(3)

式中Cx(φ)——自由节曲线x方向分量

Cy(φ)——自由节曲线y方向分量

φ——自由节曲线转角

根据非圆齿轮啮合原理，第一自由节曲线非圆齿轮旋转φ时，第一共轭自由节曲线非圆齿轮的角位移为

(4)

式中a——自由节曲线中心距

第一自由节曲线非圆齿轮为一阶非圆齿轮，第一共轭自由节曲线非圆齿轮为二阶非圆齿轮，因此，第一自由节曲线非圆齿轮旋转2π时，第一共轭自由节曲线非圆齿轮旋转π，可得计算中心距a的迭代式为

(5)

取中心距初值a0，采用进退法搜索计算出中心距a。

第一自由节曲线非圆齿轮与第一共轭自由节曲线非圆齿轮的传动比为

(6)

压力角α是衡量非圆齿轮传动优良性的重要指标，其影响传动效率，计算公式为[24]

(7)

其中

式中μ1——节曲线在该点的切线正方向与水平线夹角

α0——工具齿条的齿形角

建立节曲线凹凸性判断条件， 主动轮节曲线曲率半径ρ1计算式为

(8)

从动轮节曲线曲率半径计算公式为

(9)

节曲线无内凹部分的条件是曲率半径ρ1、ρ2分别大于零。所以无内凹的条件为

(10)

采用数值法编写程序计算式(10)的解。

1.3 差速泵计算模型

相邻两叶片最小张角为Δψmin，此时该封闭腔为最小容积，即

(11)

式中R——叶片半径，mm

r——叶轮轴半径，mm

h——叶片厚度，mm

相邻两叶片最大张角为Δψmax时，该封闭腔为最大容积，即

(12)

四叶片差速泵的排量计算式为

Q=8(Vmax-Vmin)=
4×10-3h(Δψmax-Δψmin)(R2-r2)

(13)

四叶片差速泵单泵瞬时流量计算式为

10-3hω(R2-r2)|i21-i43|

(14)

其中

式中V——排液腔容积，mL

i21——第一自由节曲线非圆齿轮副传动比

i43——第二自由节曲线非圆齿轮副传动比

φ1、φ2——第一、第二滑动叶轮转角

ω——主动非圆齿轮角速度，rad/s

不产生根切时允许齿轮的最大模数mmax的条件为[24-25]

(15)

式中ρmin——节曲线的最小曲率半径，mm

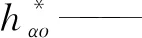
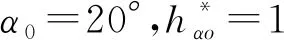
mmax=0.117ρmin

(16)

1.4 差速泵性能计算软件

根据建立的自由节曲线非圆齿轮驱动差速泵计算模型，采用Matlab编写性能分析软件，如图3所示。通过编写软件GUI人机交互界面，可以调整自由节曲线傅里叶控制点参数a0、a1、a2、b1、b2、n1、n2、m、控制点个数、选取间隔数及差速泵结构参数，通过该软件可计算差速泵的流量脉动率、排量和不根切最大模数等性能。

2 控制点对自由节曲线及差速泵性能的影响

2.1 自由节曲线控制点设置

混合高阶傅里叶非圆齿轮驱动四叶片差速泵具有较优性能，双泵脉动率22.04%已经为该节曲线驱动的最优性能[12]，本文利用自由节曲线设计非圆齿轮进一步降低脉动率，选取经过遗传算法多目标优化的1阶对2阶傅里叶节曲线为控制点选取源，通过离散后每30个序列间距提取1个控制点，共提取24个控制点，如表1所示。根据B样条曲线生成原理，为保证节曲线封闭，其中K1和K23、K2和K24设置为重叠，如图4所示。

图3 自由节曲线非圆齿轮驱动差速泵性能分析软件界面Fig.3 Performance analysis software of differential pump driven by non-circular gear with free pitch curve

2.2 控制点影响分析

自由节曲线控制点直接影响传动比以及差速泵进出口分布、排量、瞬时流量、非圆齿轮不根切最大模数等，本文以四叶片差速泵为研究对象，叶轮外半径为90 mm，叶轮轴半径为20 mm，叶片厚度为50 mm，进出口和叶片角角度差2°，输入轴转速300 r/min，叶轮平均转速为150 r/min，双泵并联相位相差90°,通过逐级改变K11、K12、K13控制点，研究分析控制点变化对单泵和双泵的脉动率、排量、不根切最大模数的影响，对应的节曲线如图5所示，差速泵性能如表2所示。

表1 初始24个自由节曲线控制点Tab.1 Initial 24 free pitch curve control points

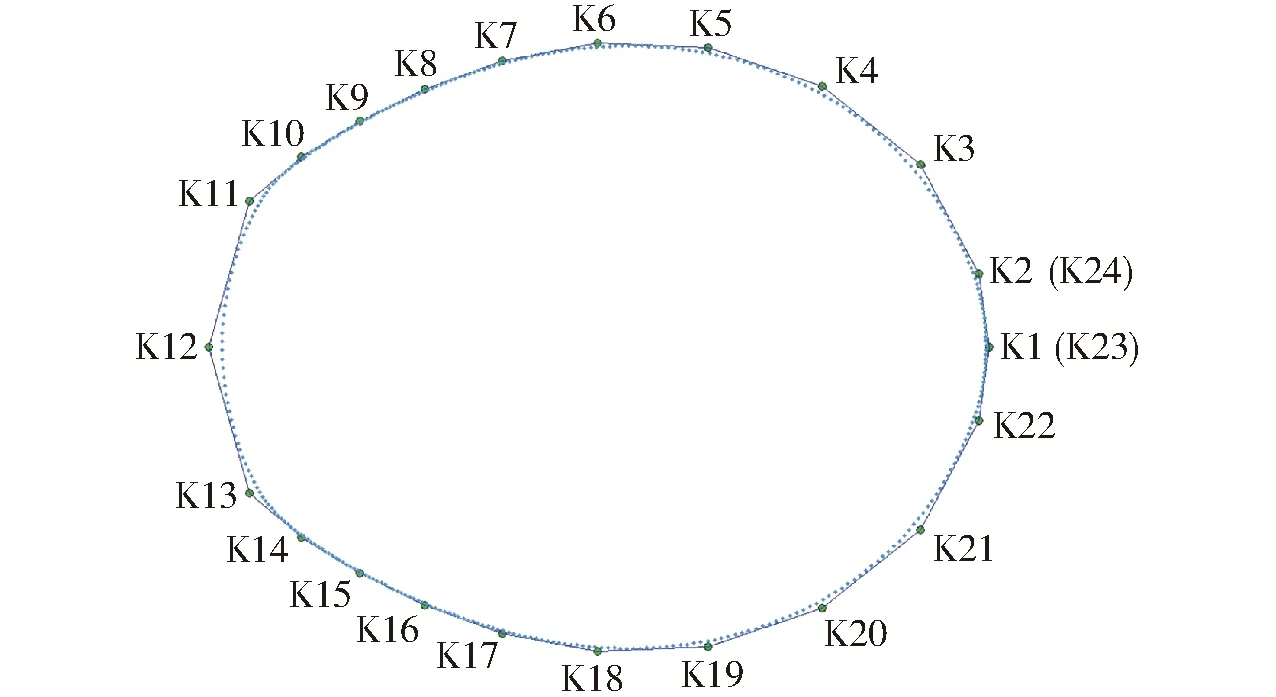
图4 24个控制点和自由节曲线Fig.4 24 control points and free pitch curve

由图5和表2可知，当节曲线为傅里叶节曲线且参数最优时，此时不根切最大模数为1.55 mm，单泵脉动率为159.8%，双泵并联脉动率为22.04%，双泵并联转排量为3 870.4 mL。自由节曲线以表1控制点为基础，设置K11(-23.64,9.99)mm、K12(-24.90,0)mm、K13(-23.64,-9.99)mm，经自由节曲线非圆齿轮驱动差速泵性能分析软件计算，不根切最大模数提升为1.83 mm，单泵脉动率为157.0%，双泵并联脉动率为21.45%，脉动率相比傅里叶非圆齿轮驱动分别降低1.8%和2.7%，双泵并联转排量为3 977.9 mL。设置K11(-23.24,9.99)mm、K12(-23.90,0)mm、K13(-23.24,-9.99)mm，不根切最大模数增加为1.84 mm，单泵脉动率152.0%，双泵并联脉动率为19.50%，脉动率相比傅里叶非圆齿轮驱动分别降低4.9%和11.5%，但其转排量为4 031.7 mL，排量增加明显。设置K11(-22.84,8.99)mm、K12(-23.90,0)mm、K13(-22.84,-8.99)mm，单泵脉动率为151.6%，双泵并联脉动率为19.20%，脉动率相比傅里叶非圆齿轮驱动分别降低5.1%和12.9%，其中不根切最大模数和转排量保持不变。

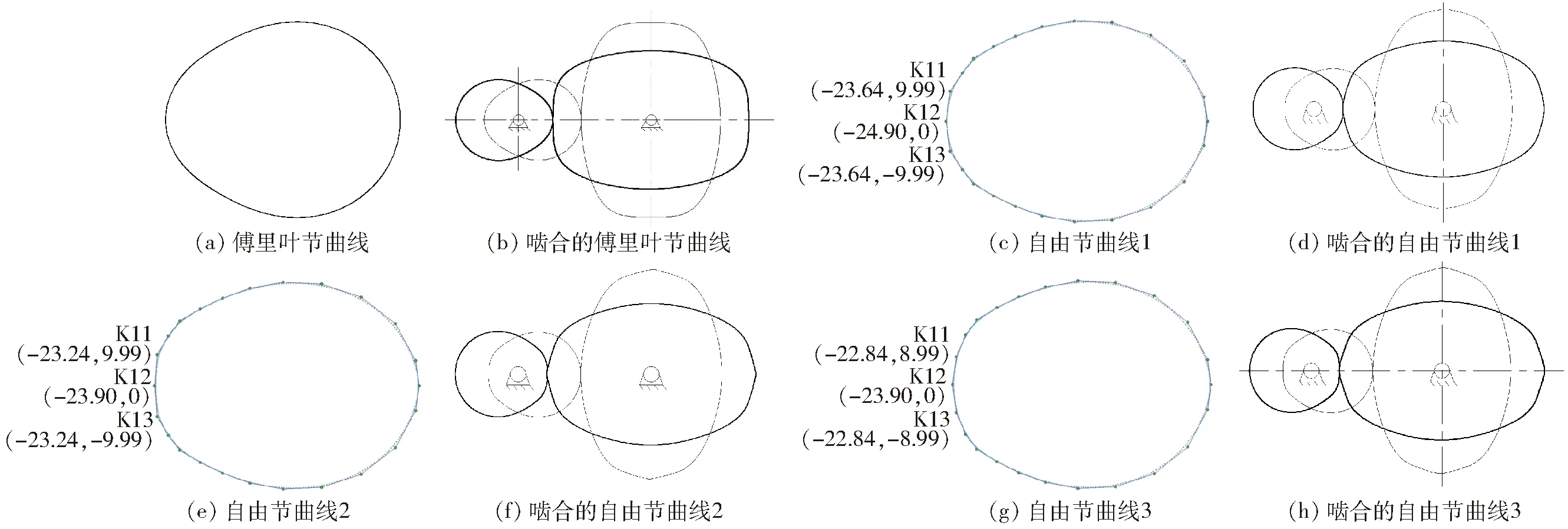
图5 不同节曲线演变过程Fig.5 Evolution process of different pitch curves

表2 控制点变化对单泵和双泵并联的脉动率、排量和不根切最大模数的影响
Tab.2 Effects of change of control point on pulsation rate, displacement and maximum modulus without undercutting of single and double pumps

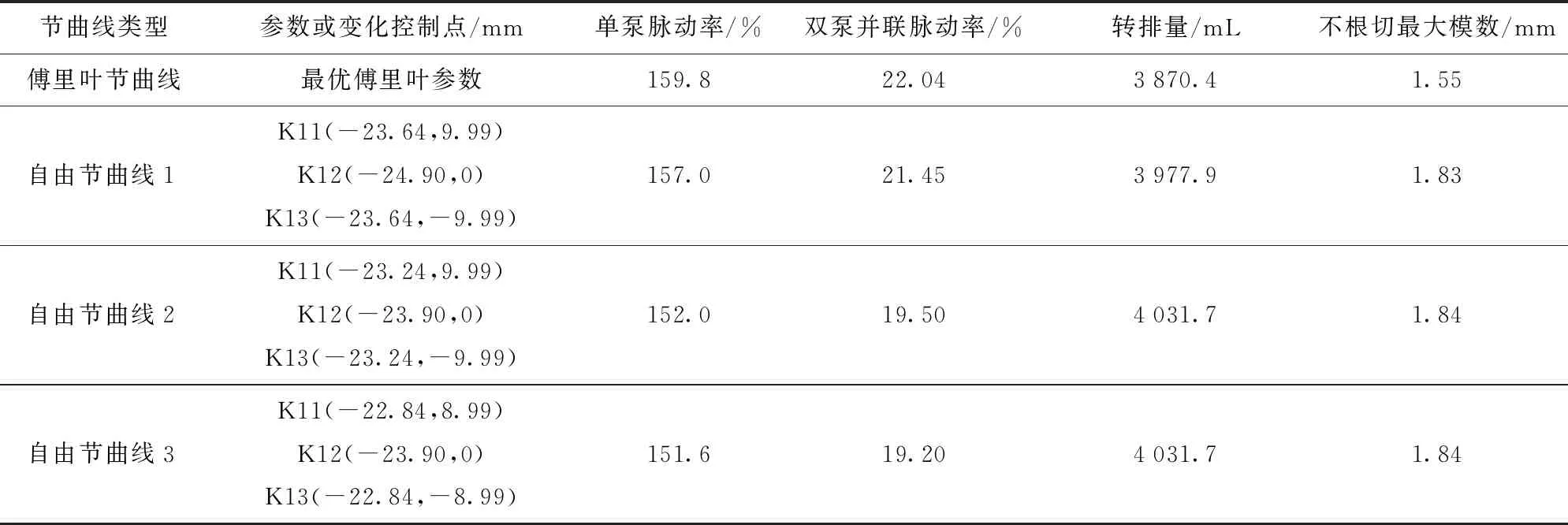
节曲线类型参数或变化控制点/mm单泵脉动率/%双泵并联脉动率/%转排量/mL不根切最大模数/mm傅里叶节曲线最优傅里叶参数159.822.043870.41.55自由节曲线1K11(-23.64,9.99)K12(-24.90,0)K13(-23.64,-9.99)157.021.453977.91.83自由节曲线2K11(-23.24,9.99)K12(-23.90,0)K13(-23.24,-9.99)152.019.504031.71.84自由节曲线3K11(-22.84,8.99)K12(-23.90,0)K13(-22.84,-8.99)151.619.204031.71.84

研究表明，自由节曲线技术可以通过有限的控制顶点构建控制多边形精确控制节曲线局部形状，以四叶片差速泵驱动的最优傅里叶节曲线为基础，通过局部修改节曲线最小曲率半径处的控制点，增加曲率半径，可增加不根切最大模数。再通过微调节曲线局部变化规律，改变叶轮传动比局部差值，根据式(14)，可调整瞬时流量局部变化规律，合适的控制点即可降低脉动率和增加排量。因此自由节曲线可实现在最优傅里叶节曲线基础上进行节曲线局部编辑，精准优化节曲线特性，进一步提升差速泵性能。由表2可知，自由节曲线非圆齿轮驱动差速泵能有效提升转排量和增加不根切最大模数，有利于提升非圆齿轮的承载能力，同时明显降低脉动率，以降低差速泵流体噪声，因此自由节曲线设计更有利于非圆齿轮驱动差速泵性能提高。

3 试验与性能比较

搭建试验台分别对自由节曲线非圆齿轮与傅里叶非圆齿轮驱动的四叶片差速泵性能进行试验比较。为了具有可比性，四叶片差速泵泵壳容积、叶轮结构及测试管路相同。差速泵试验台动力为5 kW的电机，通过变频器进行调速控制，为避免高速造成额外的冲击，变频器设定输入轴低转速，为300 r/min。由于泵源流量脉动具有高频的特点，现有流量计不能直接测试，只能采用间接方法测量，目前主要基于瞬态压力来换算脉动率，在相同负载及管路环境下，差速泵输出口的高频压力脉动可以表征不同非圆齿轮驱动差速泵泵源脉动强度。试验使用爱尔AE-H型高频压力传感器，量程为0～1 MPa，输出电压为0～10 V，数据采集装置使用阿尔泰的高频信号采集卡和采集软件，由此组成差速泵出口高频瞬态压力测试系统，通过软件将电压变化值实时转换为压力，测量差速泵瞬态压力和脉动率。试验台的非圆齿轮和差速泵如图6～8所示，性能比较如图9和表3所示。

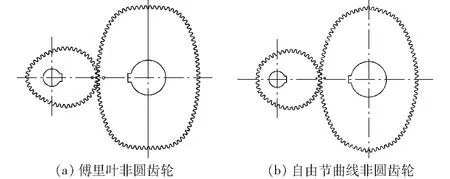
图6 试验用非圆齿轮Fig.6 Non-circular gear for test

图7 差速泵内部Fig.7 Inside of differential pump

图8 非圆齿轮驱动的差速泵试验台Fig.8 Test bed of differential pump driven by non-circular gear

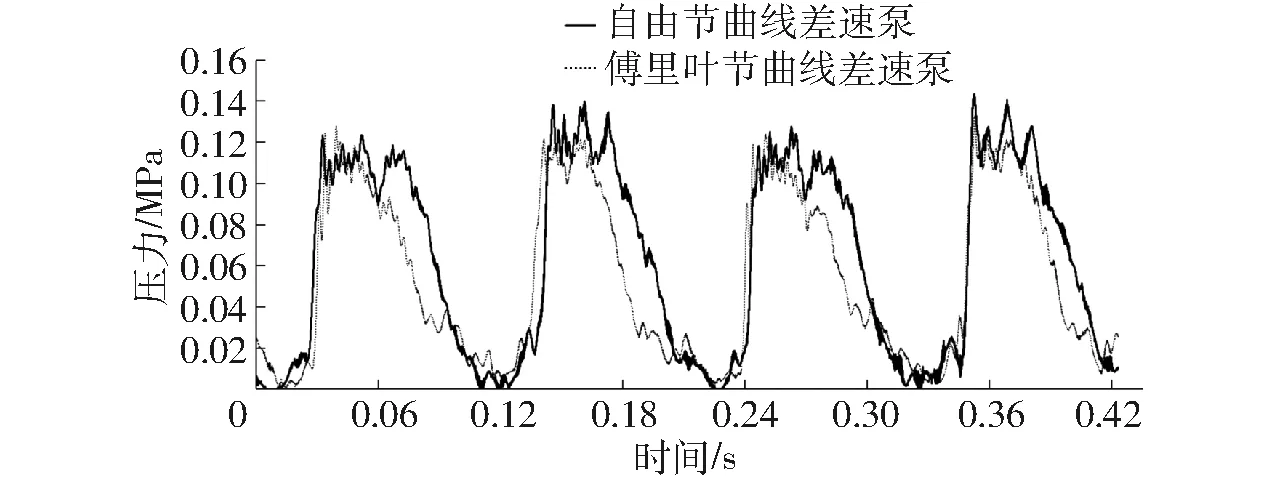
图9 不同节曲线非圆齿轮驱动的差速泵单泵出口压力曲线Fig.9 Pressure curves at outlet of single differential pump driven by non-circular gears with different pitch curves

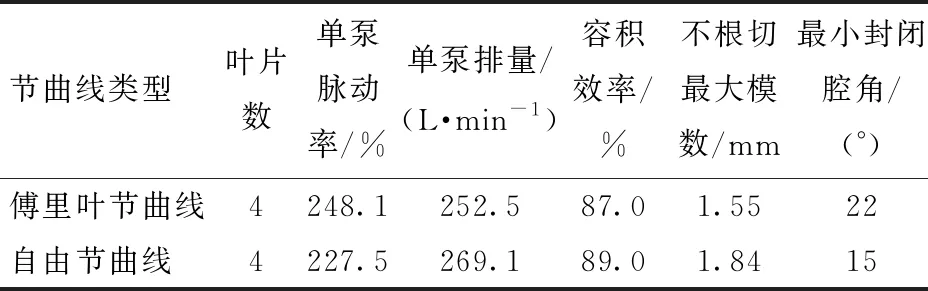
表3 同等管路条件下傅里叶和自由节曲线非圆齿轮驱动四叶片差速泵性能试验结果比较Tab.3 Performance comparison between Fourier and free pitch curve non-circular gear drive four blade differential pump under the same pipeline condition

由于自由节曲线控制点来源于傅里叶节曲线，为此自由节曲线非圆齿轮和傅里叶非圆齿轮基本轮廓非常接近，如图6所示。自由节曲线较优的局部优化能力，便于找到合适控制点优化提升差速泵性能。如图9所示，自由节曲线非圆齿轮和傅里叶非圆齿轮驱动差速泵产生的压力变化周期相同，但自由节曲线非圆齿轮驱动的差速泵出口压力峰值更宽，表明自由节曲线更有利于差速泵出口压力恒定和排量增加，压力波峰对称性更好，更有利于降低脉动率。

由表3可知，自由节曲线非圆齿轮驱动相比傅里叶非圆齿轮驱动的四叶片差速泵的排量增加6.6%，不根切最大模数增加18.7%，非圆齿轮承载能力增加，差速泵单泵脉动率降低8.3%，腔内的冲击减弱，泵内部泄漏减少，容积效率有所提升。

4 结论

(1)根据自由节曲线生成原理，建立自由节曲线非圆齿轮传动数学模型，建立自由节曲线非圆齿轮驱动差速泵的排量、流量、脉动率和不根切最大模数计算模型，编写差速泵性能计算软件。

(2)分析了控制点局部变化对差速泵不根切最大模数、排量和脉动率等性能的影响，结果表明，自由节曲线非圆齿轮有利于提高差速泵性能，可实现傅里叶非圆齿轮最优状态下通过自由节曲线的局部修正，再次提升不根切最大模数和转排量，并有效降低脉动率。

(3)对自由节曲线非圆齿轮驱动的差速泵和傅里叶非圆齿轮驱动的差速泵进行了试验，在泵壳容积和管路环境相同情况下，排量增加6.6%，不根切最大模数增加18.7%，有效提升了非圆齿轮的承载能力；差速泵单泵脉动率降低8.3%，腔内的冲击减弱，泵内部泄漏减少，容积效率有所改善。理论计算和试验结果均表明，自由节曲线非圆齿轮更有利于提升差速泵性能。