基于动态规划的电动拖拉机动力电源能量控制策略研究

2020-04-27李银平靳添絮陈亚珏

农业机械学报 2020年4期

李银平刘立靳添絮苑昆,3 陈亚珏

(1.北京科技大学机械工程学院，北京 100083； 2.北京市建筑工程研究院有限责任公司，北京 100039；3.北京安期生技术有限公司，北京 100083)

0 引言

近年来，纯电动拖拉机因具有无污染、价格低、易操作等优点而得到快速发展，纯电动拖拉机是解决传统燃油拖拉机高能耗、高污染等问题的有效措施，也是农业机械向绿色、智能化发展的主要研究方向。传统拖拉机采用柴油发动机为动力源，由于复杂的工作环境很难使发动机稳定工作在万有特性曲线的高效率区间，因此作业时存在高油耗、高排放等问题。相关研究表明，纯电动拖拉机能量利用率远高于传统燃油型拖拉机，且作业成本仅为传统燃油拖拉机的30%左右[1-2]。在农业生产过程中，纯电动拖拉机对动力电源系统的能量需求通过电机向能量控制系统发送功率需求来调节动力电池和超级电容之间的充放电工作状态，使动力电源系统工作在最佳效率状态[3]。通过确定动力电源系统各部分参数和制定合理的能量控制策略，提高纯电动拖拉机的能量利用率、动力充足性和作业效率，这对我国新能源农业机械的发展具有重要意义。

纯电动拖拉机解决了传统燃油拖拉机效率低、排污重及噪声大的问题，同时也改善了相关农业生产作业环境[4]。纯电动拖拉机分为电池拖拉机和动力电源拖拉机，在现有技术条件下，同时具有高比功率和高比能量的电池并未研发制造出来[5]，难以满足纯电动拖拉机的实际作业要求。因此，在纯电动拖拉机的动力电源系统中增加了超级电容，用于提供犁耕等大功率作业需求的功率输出，以减少蓄电池的电能消耗，进而延长了纯电动拖拉机的作业时间。动力电源系统常用的能量控制策略有模糊控制、模型预测算法以及随机动态规划等[6]。常用的优化方法有模拟退火、动态规划、遗传算法以及粒子群算法等[7-8]。动力电源系统在新能源农业机械上的应用较少，技术不够成熟。本文以纯电动拖拉机的动力电源系统为研究对象，根据纯电动拖拉机实际作业工况及其动力电源系统结构特点，在满足实际作业需求的条件下，以动力电源能量消耗最小为目标，对动力电源系统的能量控制策略通过动态规划(Dynamic programming，DP)方法进行优化，并对优化结果展开分析，提出基于规则的能量控制策略，利用仿真实验验证能量控制策略的有效性。

1 拖拉机作业工况与动力电源结构

1.1 拖拉机作业工况

拖拉机的主要作业工况是通过不同的农机工具进行犁耙耕地、播种施肥、洒药除草、农作物收获等多种作业，拖拉机悬挂农机具进行农业生产或者牵引挂车进行运输作业，其作业工况大体分3种[9]：工况Ⅰ：低速慢行作业，农田旋耕、挖掘沟槽及栽培耕种等；工况Ⅱ:农田间生产作业，深耕施肥、除草施药等；工况Ⅲ:农作物收获及运输作业。随着农产品需求量的增大，目前70%以上的农作物生产运输必须依靠拖拉机完成，拖拉机是农业生产活动的主要运输工具。由于拖拉机作业工况的多样性，其牵引阻力也随着发生变化。当负载需求功率为全功率的80%以上时称为重载模式; 负载需求功率为全功率的20%～80% 时称中载模式；负载需求功率为全功率的20%以下时称轻载模式。拖拉机在犁地作业时，牵引阻力比较大，属于重载模式；在除草施肥、移栽等作业时，属于中载模式；在空车行驶、播种洒药等作业时，属于轻载模式[10]。对不同的工况模式，拖拉机动力源系统的调控工作模式不同，因此只有保障动力电源系统各组成部分协同有效运行，输出能量高效率利用，才会提高生产作业效率。图1为3种工况模式下的某拖拉机农田作业时采集的系统负载功率变化曲线，0～50 s是工况Ⅰ，50～100 s为工况Ⅱ，100～150 s是工况Ⅲ，依次循环3种工况。在犁耙耕地重载工况下，为了实现犁耙农具插入田地并开始耕地时需要较大功率, 而在施肥洒药等中、轻载工况模式下，整车负载需求功率较小。因此需要建立高效的动力电源系统能量控制优化策略，合理分配动力电源系统的功率，在满足拖拉机实际运行需求的同时降低能量消耗。

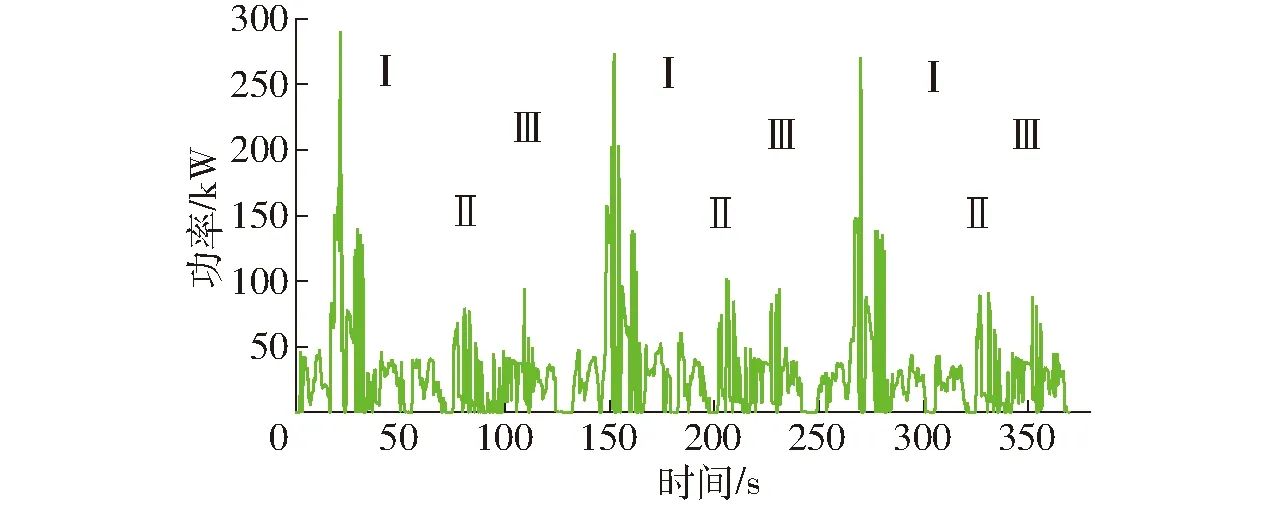
图1 某拖拉机系统负载功率变化曲线Fig.1 Load power change curve of tractor system

针对拖拉机作业工况的复杂性，设计了以超级电容(Super capacitor, SC)和蓄电池为复合的双动力电源(Dual-source energy supply system，DESS)的纯电动拖拉机，如图2所示。使用超级电容+蓄电池作为动力电源的纯电动拖拉机，可满足纯电动拖拉机在中轻负载作业工况下长时间运行的能量需求，而当拖拉机作业负荷功率需求突然增大时，超级电容与蓄电池协同工作，从而防止蓄电池频繁大电流放电，保障了蓄电池的安全，提高了电池使用寿命。为充分利用动力电源系统能量，通过能量控制策略合理有效地分配蓄电池和超级电容两者的输出功率，实现能量按最佳路线流动，从而提高能量利用率[11-12]。本文对动力电源系统的结构进行选型分析，对动力电源系统数学模型进行计算，对能量控制策略进行数学抽象，同时结合复合电源各自的放电特性，制定了以动态规划为核心的能量优化控制策略，与基于规则的能量控制策略相比，通过仿真实验验证了基于动态规划的能量优化控制策略在节能降耗方面的有效性及适用性。

图2 纯电动拖拉机复合动力电源结构示意图Fig.2 Structural sketch of compound power supply for pure electric tractor

1.2 动力电源系统结构

目前动力电源的拓扑结构主要有4种：蓄电池与超级电容器直接并联，超级电容只将电能进行存储和释放，但是缺少DC/DC变换器的变流作用，蓄电池和超级电容器不受控制，称之为被动结构；由蓄电池先与DC/DC变换器串联再与超级电容并联，称之为蓄电池与DC/DC串联式半主动结构；由超级电容先与DC/DC变换器串联再与蓄电池并联，称之为超级电容与DC/DC串联式半主动结构；由蓄电池和超级电容器各自串联一个DC/DC变换器后再并联，称之为主动结构[13-14]。不同动力电源拓扑结构的特性对比如表1所示。

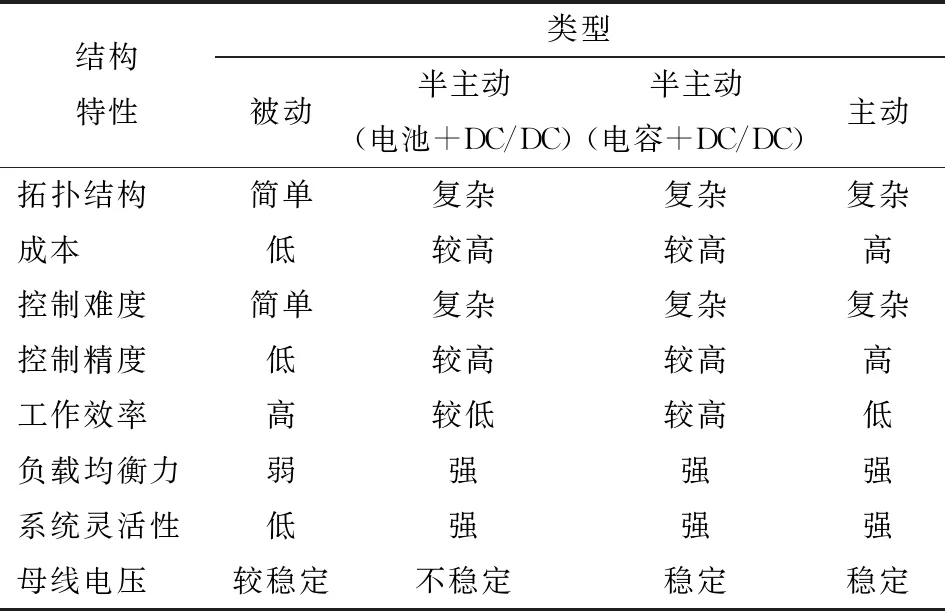
表1 动力电源不同拓扑结构特性对比Tab.1 Comparison of different topological characteristics of power supply

由于纯电动拖拉机的作业特点比一般常用车辆复杂，对动力电源系统的控制有较高的要求，综合考虑纯电动拖拉机的实际结构以及成本等因素，被动结构无法满足实际控制需求，而主动结构成本过高且控制复杂[15]，因此选择超级电容与DC/DC串联式的半主动结构作为纯电动拖拉机的动力电源系统拓扑结构，如图3所示，超级电容与双向DC/DC串联后再与蓄电池并联到功率总线，其不仅能够满足控制需求，而且控制难度比主动结构低，且精度高、成本较低、工作效率高，这些均符合对纯电拖拉机动力电源系统的一些基本要求。

图3 超级电容与DC/DC串联式半主动拓扑结构Fig.3 Semi-active topology of super capacitor and DC/DC series

2 动力电源系统模型

目前动力电源系统的组成主要有蓄电池、超级电容器和双向DC/DC变换器。根据纯电动拖拉机运行时对动力电源系统的特性要求，对电池、超级电容器及双向DC/DC变换器建立合适的模型，从而保证计算仿真结果的可靠性和有效性。

2.1 蓄电池组模型

鉴于蓄电池充放电过程是一种很复杂的非线性过程，建立精确模拟蓄电池充放电工作过程的模型很难。为了方便建立动态规划问题，采用Rint模型[16-18]，其相关模块计算式如下：

电流模块计算式为

(1)

式中IB——电池电流，A

UB——电池开路电压，V

RB——电池内阻，Ω

PBout——电池输出功率，W

SOC模块计算式为

(2)

式中BSOCt——电池在t时刻的荷电状态

CB——电池容量，A·h

根据电池当前SOC值和需求功率，计算出电池组的端电压和内阻。首先判断蓄电池处于充电还是放电状态，再根据当前的SOC值和蓄电池的温度，采用插值查表法通过查图4可得单个电池在该状态下的内阻，根据串并联关系求得电池组的内阻，最后计算端电压，即

Uload=UB-IBRB

(3)

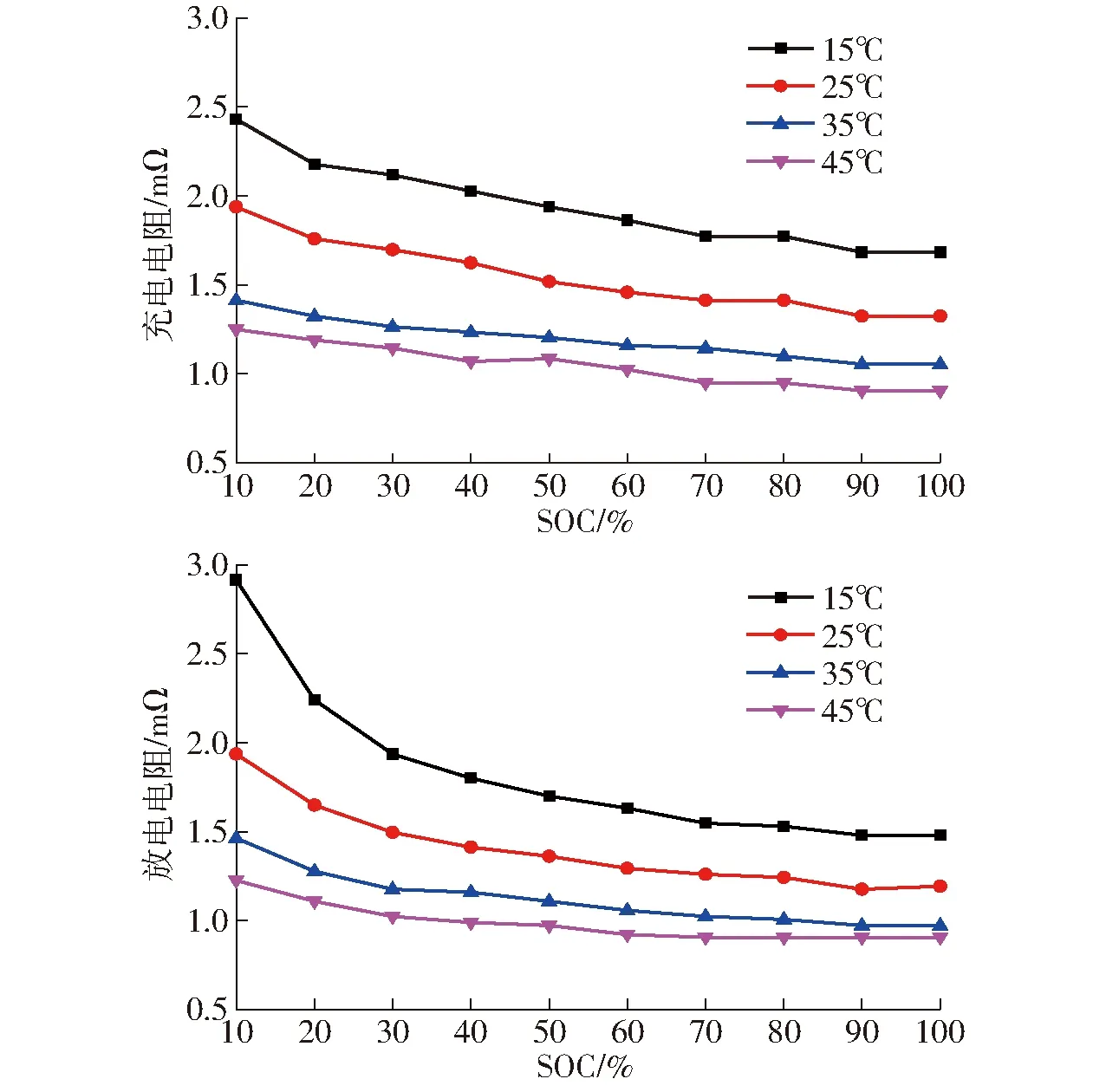
图4 电池单体充/放电电阻与SOC值的关系Fig.4 Relationship between battery cell charging/discharge internal resistance and SOC value

蓄电池消耗功率模块计算式为

PB=IBUB

(4)

式中PB——电池消耗总功率，W

2.2 超级电容器组模型

超级电容的等效模型采用经典的RC模型，而在RC模型中的等效并联电阻很大，通常经过长期的放置才会体现，因此忽略不计。将模型简化成与电池内阻模型相类似的等效模型[19-21],超级电容器组相关模块的计算如下：

电流模块计算式为

(5)

式中IUC——超级电容电流，A

UUC——超级电容电压，V

RUC——超级电容内阻，Ω

PUCout——超级电容输出功率，W

PUC=IUCUUC

(6)

式中PUC——超级电容消耗总功率，W

SOC模块计算式为

(7)

式中UCSOC——超级电容荷电状态

UUCmax——超级电容最大电压

根据超级电容需求功率的正负判断超级电容是放电状态还是充电状态，根据电流利用插值查表法通过查图5可得在该状态下超级电容单体的内阻，乘以串联个数再除以并联个数便可得到超级电容组的内阻，而超级电容开路电压计算式为

(8)

式中UUCt——超级电容在t时刻的开路电压，V

CUC——超级电容的容量，F

UUC0——超级电容初始开路电压，V

2.3 双向DC/DC变换器模型

DC/DC变换器的建模方法主要包括数值法和解析法。双向DC/DC变换器是将原直流电通过调整其PWM(占空比)来控制输出的有效电压以改变供给电机或超级电容的电压。本文不需考虑其内部机理的变化，只考虑其效率。因此利用查表法建立双向DC/DC的效率模型，其效率变化曲线如图6所示[22]。

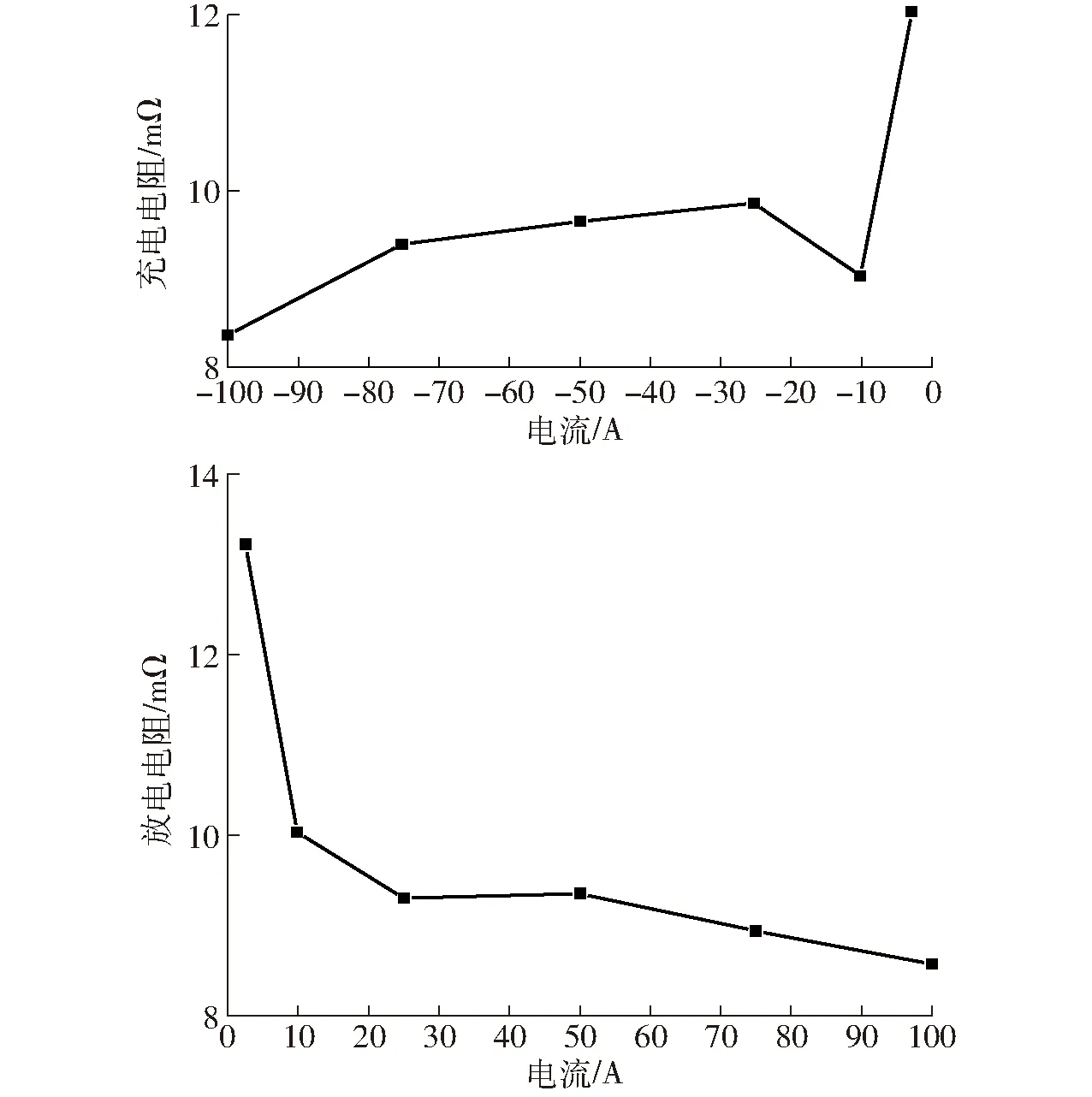
图5 超级电容单体充/放电电阻Fig.5 Internal resistance value of super capacitor unit charging/discharge

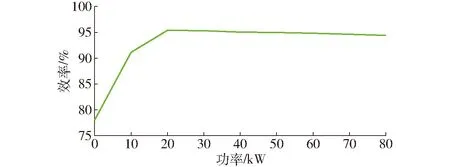
图6 双向DC/DC变换器效率随功率的变化曲线Fig.6 Efficiency change curve of bidirectional DC/DC with power

3 基于动态规划的控制策略

由蓄电池组和超级电容器构成的动力电源系统的功率分配可以看成是以时间为阶段的多阶段决策问题，而动态规划是求解多阶段决策过程最优化的数学方法。多阶段决策过程也称多步决策过程，即把多阶段过程转换为一系列子阶段问题，利用各阶段之间的关系逐个求解，因此可以将动态规划用于动力电源系统的能量控制策略中。动态规划应满足最优化原理和无后效性。动态规划的基本思想是将待求解问题分解成若干个子问题，采用Bellman递推方程求出各个子问题的解，最后从这些子问题的解中得到原问题的最优解，因此对于多阶段决策问题，采用动态规划能够很好地解决[23-25]。

3.1 动态规划问题

由于纯电动拖拉机的工况比较复杂，几乎没有相关作业工况适合能量回收，并且拖拉机的应用环境较严峻，电制动无法保障其安全性，因此暂不考虑制动能量回收的情况。

以纯电动拖拉机在作业工况中动力电源系统能量消耗最少为优化目标。建立目标函数为

J=∑(EBt+EUCt)

(9)

式中EBt——电池在t时段的消耗总能量，J

EUCt——超级电容在t时段的消耗总能量，J

将时间t划分各个阶段，时间划分越细则DP的结果准确性越高，以采样时间0.1 s作为阶段间的时间间隔。在每一阶段，纯电动拖拉机的总负载功率Pdem作为输入变量。且功率关系式为

Pdem=PBout+PUCout

(10)

由于蓄电池和超级电容内阻及DC/DC的存在，因此在计算电池和电容的输出功率时需考虑这部分的能量损失。由式(10)得总负载功率，因此只需控制超级电容的输出功率就可求得蓄电池的输出功率，而超级电容的输出功率又与SOC值有直接的关系，且SOC值与电容的开路电压呈比例关系，故选择超级电容的开路电压UUCt为状态变量，其动态规划算法求解示意图如图7所示，设定状态变量取值间隔为0.2 V，则状态转移方程为

UUC(t+1)=UUCt-ΔUUC

(11)

式中 ΔUUC——超级电容开路电压变化量，V

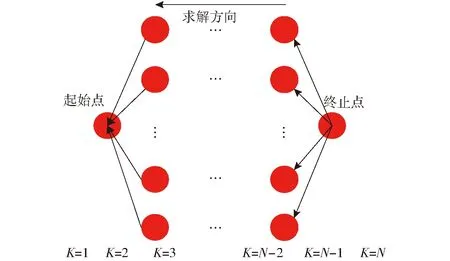
图7 动态规划求解示意图Fig.7 Dynamic programming solution diagram

为了方便计算在每个阶段下超级电容的输出功率，选择ΔUUC为决策变量。则在每个阶段下，超级电容消耗总能量EUC和消耗总功率PUC计算式为

(12)

PUC=EUC/Δt

(13)

式中 Δt——时间间隔，s

根据式(5)～(7)可以求出超级电容的输出功率PUCout和荷电状态SOC等参数。根据式(10)求出电池输出功率PBout。根据式(1)～(4)求出电池消耗功率PB和荷电状态SOC等参数后，求出电池的消耗总能量EB为

EB=PBΔt

(14)

在优化过程中不等式约束条件为

(15)

等式约束条件为

UCSOC0=UCSOCend

(16)

式中UCSOCend——工况结束后超级电容的开路荷电状态

由于本文采用纯电动拖拉机在轻载、中载、重载连续3个作业工况下的数据，因此为了保证之后规则提取的有效性，在每个工况结束后，都需要保证超级电容的SOC值与初始值相同。

3.2 优化结果

此优化过程中，超级电容和电池单体参数均参照文献[26]。由于电池的内阻和开路电压均与荷电状态SOC值有关，但电池在作业工况时间下SOC值变化很小，故将电池的内阻和开路电压看作定值，而超级电容的内阻与电流有关，在DP计算时电流变化比较频繁，为了保证结果的准确性，需将超级电容内阻看作电流函数，利用查表法代入计算。通过参数匹配计算，电池组和超级电容组参数如表2所示。

表2 电池组和超级电容组参数Tab.2 Battery pack and super capacitor group parameters

为了确定超级电容初始电压，针对每个工况设置不同的超级电容电压初始值，分别运用动态规划进行优化，通过Simulink建模仿真，以超级电容初始电压为自变量得到不同初始电压与其对应工况能量消耗关系曲线，如图8所示。

图8 不同初始电压对应的作业工况能量消耗曲线Fig.8 Curves of energy consumption for different initial voltages under operating conditions

由图8可以看出，当初始电压为525 V左右时，工况消耗的能量最少，且初始电压在470～550 V范围时，工况能量消耗基本相同，因此为了方便之后基于规则控制策略的提出，故将初始电压设为550 V，对3个工况利用动态规划进行优化，优化结果如图9、10所示。

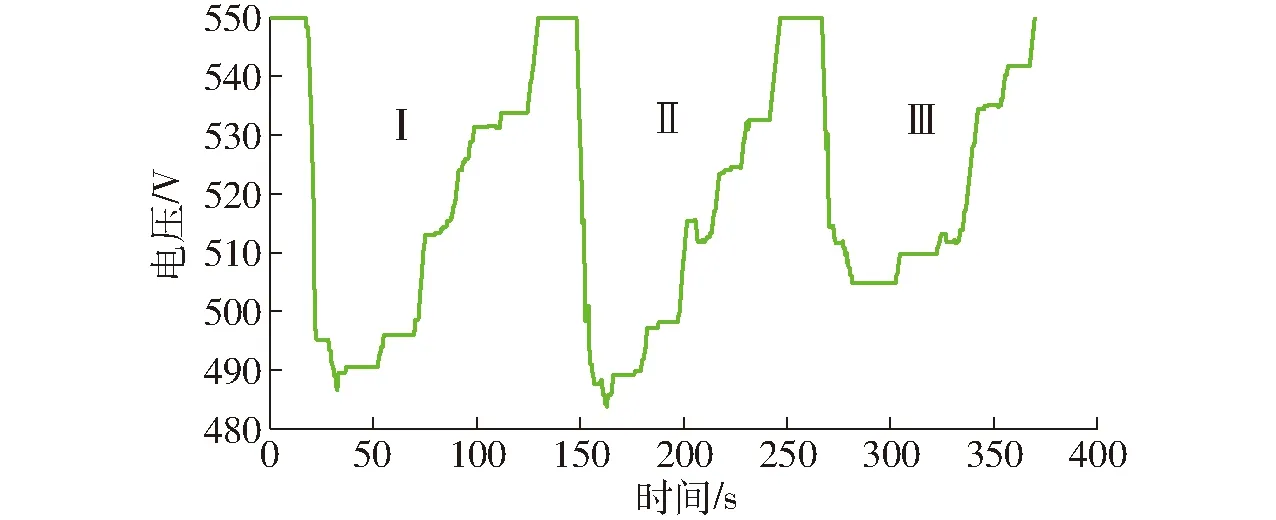
图9 动态规划优化后超级电容的电压Fig.9 Voltage of super capacitor optimized by dynamic pogramming

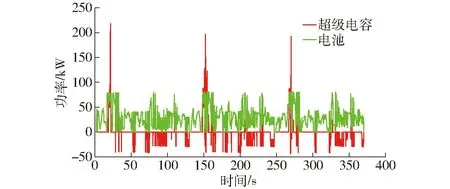
图10 动态规划优化后超级电容和电池的输出功率Fig.10 Output power of super capacitor and battery optimized by dynamic programming

对图10输出功率曲线进行积分计算即可得到动力电源系统的消耗总能量为10 738.15 kJ。

3.3 基于规则的能量控制策略制定

在系统负载功率需求曲线中并没有负的功率，即没有制动能量部分的数据，因此规则制定中并不考虑制动能量回收策略。从图9可以看出，超级电容在每个工况开始都处于最大工作电压状态，之后在犁耕等重载工况开始阶段瞬时放出大功率，然后为了满足超级电容在工况结束后的荷电状态SOC值与初始值相同，以小功率进行持续充电；从图10可以看出，在作业工况过程中，以电池放电为主，而超级电容几乎只在重载作业工况大功率需求阶段提供能量，而其余时间电池在提供负载功率的同时以小功率给超级电容充电，若超级电容已充满电，则由电池单独供电。

通过对以上纯电动拖拉机作业工况功率输出的分析，可得以下规则：

(1)超级电容随时输出大功率，因此保证超级电容在作业开始前超级电容的荷电状态值UCSOC达到设定最大值UCSOCmax。

(2)功率大于PBmax时，电池从最大功率PBmax开始放电，超级电容补足剩余功率需求。

(3)功率需求小于PBmax且超级电容的UCSOC值为UCSOCmax时，由电池单独供电。

(4)功率小于电池最大功率PBmax且超级电容的UCSOC低于UCSOCmax时，由电池提供负载功率的同时以恒定小功率PBlow持续为超级电容充电，并保证电池的输出功率不超过PBmax。

(5)当功率小于0时，由超级电容承担全部的制动能量。

基于以上规则，得到能量控制策略流程如图11所示。

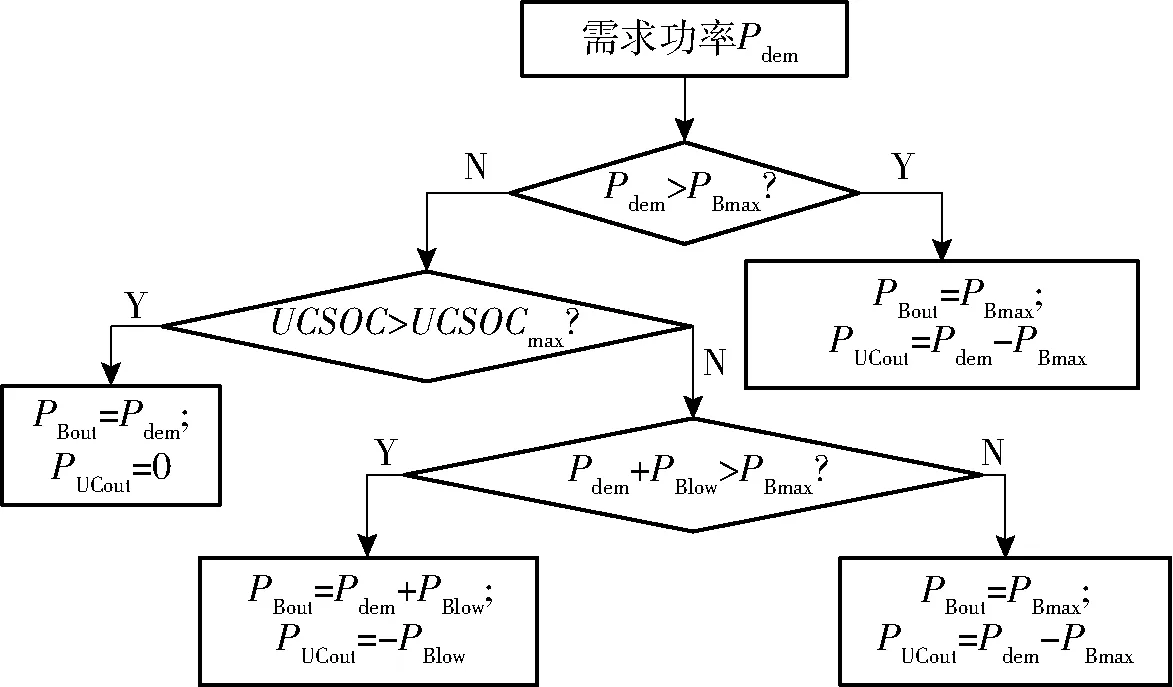
图11 能量控制策略流程图Fig.11 Flow chart of energy control strategy

4 仿真结果分析

根据图11所示的能量控制策略流程图，利用Simulink模块进行仿真，结果如图12、13所示。

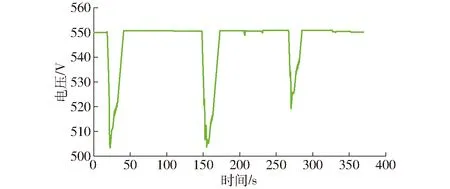
图12 基于规则优化后超级电容的电压变化曲线Fig.12 Voltage of super capacitor based on rule optimization

图13 基于规则优化后超级电容和电池的输出功率Fig.13 Output power of super capacitor and battery based on rule optimization

对图13输出功率曲线进行积分计算可得到动力电源系统的消耗总能量为12 671.02 kJ，可得基于动态规划的能量控制策略相比基于规则的能量控制策略能量消耗减少了1 932.87 kJ，即能量消耗减少率为18%，基本上已经达到DP优化的结果，证明了基于动态规划的能量控制优化策略在节能降耗方面的有效性。