灌水量和地下水调控对干旱地区土壤水盐分布的影响

2020-04-27史海滨郭珈玮王国帅付小军李正中

农业机械学报 2020年4期

史海滨郭珈玮周慧王国帅付小军李正中

(1.内蒙古农业大学水利与土木建筑工程学院，呼和浩特 010018；2.内蒙古河套灌区解放闸灌域管理局沙壕渠试验站，巴彦淖尔 015400)

0 引言

土壤盐分是制约干旱和半干旱地区作物生长及产量的重要因子之一[1-3]，全球大约有33%的农业用地被盐化[4]。不合理的灌排制度是导致土壤发生次生盐渍化的主要原因[5]。目前，灌溉农田占中国耕地面积的39.6%[6]，内蒙古河套灌区位于我国典型的干旱地区，是亚洲最大的一首制平原引水灌区，总干渠长180.85 km[7-8]。近年来，节水改造的实施致使灌区传统的排水控盐技术受到限制，淋洗水量不足使盐分在土壤表层积累[9]。同时，灌区浅地下水埋深也增加了因潜水蒸发带来盐分的几率，进一步加大土壤盐碱化的风险[10]。灌区内部灌溉水、土壤水和地下水三者之间联系紧密，采用灵活的水分配置政策[11]、将地下水位调控至合理埋深对于实现水资源有效利用、减轻土壤盐渍化将起到重要作用。

近年来，国内外学者关于不同作物灌溉制度的研究方法大致分为两类。第1类是通过研究作物需水量和水量平衡来估算各种作物的灌溉需求；第2类研究侧重于通过模型模拟来制定科学的灌溉制度和优化农业管理[12-16]。但上述研究均未考虑地下水对作物灌溉制度的影响。灌区作物的灌溉间歇期长，间歇期作物需水主要靠地下水补给。地下水位过低，不能满足作物需水量，甚至会导致作物减产；地下水位过高，又会增大表层土壤积盐的概率。因此，对灌区地下水位的合理调控极为重要。研究表明，地下水位不同，土壤水与地下水的相互作用程度不相同，导致作物所需灌溉水量也不同[17-18]。理清GSPAC系统中的水盐运移规律，制定合理的灌溉制度及地下水埋深，发挥两者对土壤水的调节作用，对控制灌区土壤次生盐渍化的产生以及对作物正常生长发育具有重要意义。

本研究以灌区主要作物向日葵农田作为研究对象，基于田间试验数据，构建田间尺度饱和-非饱和土壤水盐运移数值模型，利用HYDRUS-2D模型模拟不同灌水量条件下的土壤水盐运移规律，通过调节灌水量确定最优的灌溉方案，并结合对地下水埋深的调控寻求一种适合当地农业生产的节水灌溉、防治土壤盐渍化的农田水盐调控方案，为当地农业灌溉水合理利用和水盐调控提供理论依据。

1 材料与方法

1.1 试验区概况

试验区位于河套灌区杭锦后旗南小召永胜五队(40°48′N，107°5′E, 海拔1 038 m)，多年平均气温6.9℃，年日照时数3 189 h，相对湿度51%，年均风速为2.8～2.9 m/s。年总辐射量为6 151.2～6 383.1 MJ/m2，大于10℃年积温为3 180℃，全年日照充足，昼夜温差大，降水量集中，蒸发强烈，研究区参考作物腾发量(ET0)和降雨量如图1所示。试验期为每年6月初—9月末，向日葵播种时间分别为2017年6月1日和2018年6月3日，收获时间分别为2017年9月25日和2018年9月26日。研究区土壤物理性质如表1所示，土壤质地以粉壤土为主，田间持水率为37%，凋萎系数为0.12。试验区土壤盐碱化严重，土壤表层电导率为1.5 dS/m，土壤容重1.56 g/cm3。以2018年典型区地下水位监测数据为例，地下水埋深变化范围在47.89～165 cm，平均地下水电导率为4.18 dS/m。研究区主要依靠灌水进行洗盐来维持作物生长，每年进行3次灌水，其中生育期只进行1次，其余2次为春播前灌水与秋浇，2017、2018年生育期分别在7月6日、7月7日灌水95、92 mm。

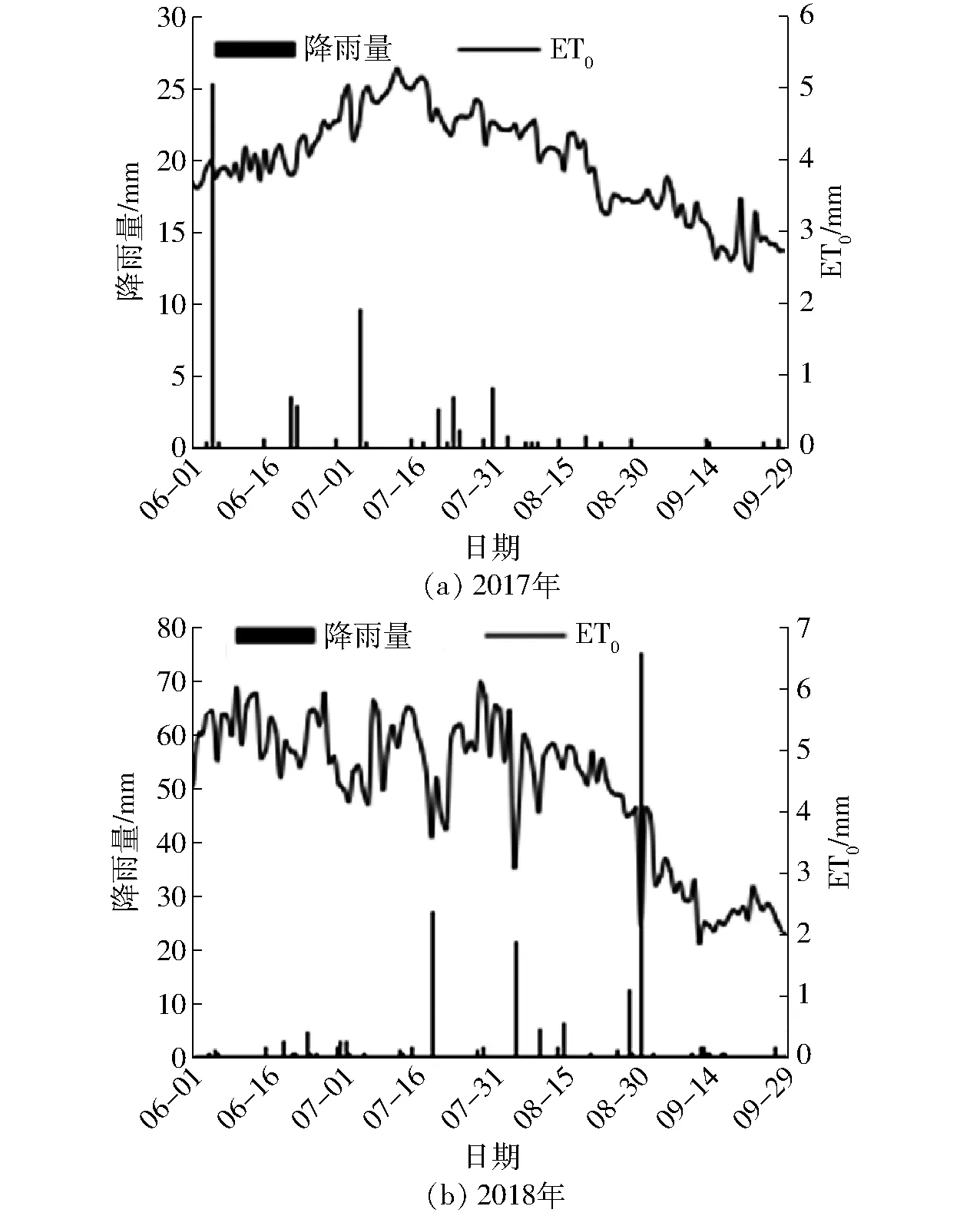
图1 2017年与2018年全生育期ET0和降雨量Fig.1 ET0 and rainfall during whole growth periods in 2017 and 2018

表1 土壤物理性质
Tab.1 Soil physical properties

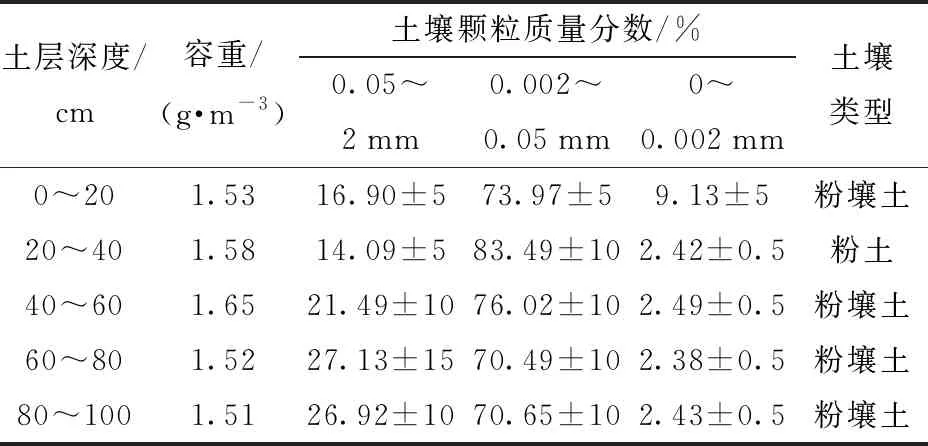
土层深度/cm容重/(g·m-3)土壤颗粒质量分数/%0.05～2mm0.002～0.05mm0～0.002mm土壤类型0～201.5316.90±573.97±59.13±5粉壤土20～401.5814.09±583.49±102.42±0.5粉土40～601.6521.49±1076.02±102.49±0.5粉壤土60～801.5227.13±1570.49±102.38±0.5粉壤土80～1001.5126.92±1070.65±102.43±0.5粉壤土

1.2 试验方法与数据来源

研究区位于东涨渠内部，地势整体为西北高东南低，北部为道路，西部为机缘支渠，东部为永胜到先锋干渠，南部为几夜渠，四周以道路和支渠为边界，可以看作相对独立的灌溉系统。试验区选定在2.8 hm2向日葵农田内开展，东西长140 m，南北长200 m，灌溉方式为畦灌。如图2所示，研究区内布设地下水位监测孔，孔深4 m。2017年每隔10 d采用土钻取土法取样，取样深度为120 cm，灌水前3 d和灌水后连续10 d取样，观测时间为一水、二水、秋浇，本文只对生育期灌水进行研究。土壤含水率采用干燥法测定，含盐量采用5∶1水土质量比浸提电导法测定。2018年在25、45、65、85 cm土壤深处加设ECH20型土壤水分温度及电阻率检测系统及CTD-10型地下水自动记录仪，每隔1 d自动监测土壤含水率、电导率，地下水位与地下水电导率。且每隔10 d采用土钻取土法取样，对仪器进行验证。在试验地放置微型蒸发器测量土壤蒸发量。用盒尺测量向日葵各生育期内的株高、叶面积，每隔10 d监测1次。

土壤指标观测包括：土壤含水率、电导率；地下水指标：地下水位、电导率；灌水指标：灌水量、时间、灌溉水电导率；作物指标：向日葵各生育期内的株高、叶面积。

图2 试验区土壤水盐监测点布置图 Fig.2 Layouts of experimental site for soil water and salt monitoring

1.3 数值计算与分析方法

1.3.1样品处理与分析

将采集的土样带回实验室自然风干后碾碎过1 mm筛备用。所有土样均制备5∶1水土浸提液，测定其电导率(EC1∶5)。

选取全部96个土壤样品，通过相关分析得到自动监测仪所测电导率，换算成土壤EC1∶5的换算关系为

S1=0.959 5S2+0.150 5
(r=0.975，p<0.05)

(1)

式中S1——自动监测仪电导率，dS/m

S2——土壤样品EC1∶5，dS/m

土壤全盐量计算公式为[19]

C=6.9EC1∶5-0.2

(2)

式中C——土壤全盐量，g/kg

EC1∶5——水土比5∶1土壤浸提液电导率，dS/m

使用由实验室测试开发的经验公式，将地下水电导率转换为地下水含盐量[20]。公式为

TDS=0.69EC

(3)

式中TDS——地下水含盐量，g/L

EC——地下水电导率，dS/m

1.3.2土壤洗盐率

洗盐率指0～120 cm平均土壤剖面在灌溉后某一时期与灌溉前相比土壤含盐量的减少率，其计算公式为

(4)

式中St——土壤洗盐率，%

et——灌溉后某一时期土壤含盐量，g/kg

e0——灌溉前土壤含盐量，g/kg

1.3.3边际土壤洗盐率

边际土壤洗盐率指每增加一个单位的灌水量所增加的土壤洗盐率。表示其他条件固定不变时，由灌水量所带来的最大土壤洗盐率的变化，其计算公式为

(5)

式中S(Zt)——边际土壤洗盐率，%

Q1、Q2——不同时刻的灌水量，m3/hm2

St1、St2——某一时刻灌水量为Q1、Q2的土壤洗盐率，%

2 模型建立

2.1 基本方程

土壤水分运移数学方程为

(6)

式中θ——土壤体积含水率，cm3/cm3

z——垂向坐标，cm，零点取在地面，地面以上为负

t——时间，d

h——土壤水势，cm

K(θ)——非饱和土壤导水率，cm/d

S(z,t)——单位时间单位体积土壤中根系吸水率，d-1

土壤水力函数为[21]

(7)

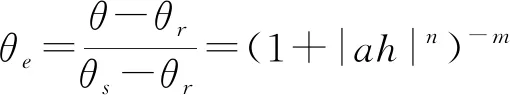
(8)

m=1-1/n(n>1)

(9)

式中θe——土壤相对饱和度

θr、θs——残余土壤含水率、饱和土壤含水率，%

Ks——土壤饱和导水率，cm/d

n、m、a——经验参数

l——孔隙关联度参数，一般取平均值0.5

以土壤可溶盐为研究对象，以土壤溶液的盐分浓度为主要指标，建立土壤二维饱和-非饱和溶质运移数学模型。土壤盐分运移数学方程为

(10)

式中cz——土壤溶液的盐分质量浓度，g/cm3

Dzz——水动力弥散系数，cm2/d

qz——土壤水入渗率，cm/d

c——液相的盐分质量浓度，g/cm3

2.2 定解条件确定

二维土壤水流的初始条件和边界条件如下：

初始条件

θ(z，t)|t=0=θ0(z) (Z≤z≤0)

(11)

上边界

(12)

下边界

h(z，0)|z=Z=hb(t>0)

(13)

式中Z——土壤水盐模型模拟深度，cm

ε——垂向水流交换强度，cm/d

hb——下边界处负压，cm

θ0——土壤初始含水率，cm3/cm3

模型上边界为随时间变化的第2类边界条件，根据实测数据(如降雨量、灌水量)计算出的潜在蒸发蒸腾量逐日输入模型进行模拟。根据2017—2018年实测地下水埋深最大值为165 cm，考虑地下水补给,故将模拟区深度设为200 cm, 并将下边界设为变水头边界，逐日赋值地下水头，左右两测边界设为零通量边界。

二维土壤盐分的初始条件和边界条件如下：

初始条件

c(z，t)|t=0=c0(z) (0≤z≤Z)

(14)

上边界

(15)

下边界

c(z,0)=ci(z=Z,t>0)

(16)

式中c0——初始盐分质量浓度，g/cm3

ε1——蒸发强度，cm/d

ci——z层土壤盐分质量浓度，g/cm3

2.3 模型构建

2.3.1时间离散

模拟整个生育期(2018年6月1日—9月30日)共122 d的数据。根据收敛的迭代次数调整时间步长，采用变时间步长剖分方式。初始时间步长为0.1 d，最小时间步长为0.001 d，最大时间步长为5 d。

2.3.2空间离散

模拟深度取至地面200 cm，采用矩形网格剖分，垂直方向剖面上的土壤为2种土壤质地，分别是0～20 cm、40～200 cm粉壤土和20～40 cm粉土。并按照等间距剖分为40个单元层，每层厚5 cm，水平方向取剖面长度为100 cm，等间隔剖分为10层，每层厚10 m。

2.3.3根系吸水项

根系吸水的影响函数采用Feddes函数[22]，定义为

S(h)=∂(h)SP

(17)

其中

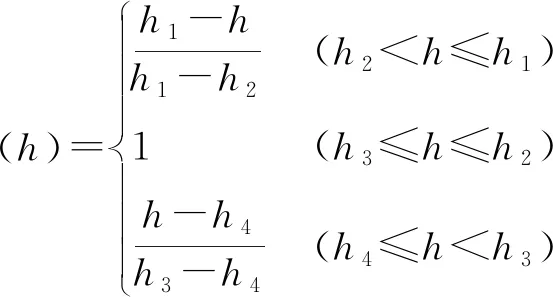
(18)

(19)

式中S(h)——单位时间内植物根系从单位体积土壤中吸取的水体积

∂(h)——土壤水压力响应函数，为给定土壤压力水头的无因次系数(0≤a≤1)

SP——潜在最大吸水速率，d-1

h1、h2、h3、h4——影响根系吸水的土壤水势阈值

Tp——潜在蒸腾速率，cm/d

Lz——根系深度，cm

Lx——土壤剖面上根系的宽度，cm

Lt——发生蒸腾作用的土壤表面宽度，cm

不同作物的根系吸水参数，通过前人研究成果确定[23]。

2.3.4潜在蒸腾速率的计算

HYDRUS模型通过输入潜在蒸散量来完成作物-土壤水分交换运移过程。并在运算过程中通过一定的比例因子将潜在蒸散量转换成实际的蒸散量。

ET0由FAO推荐的Penman-monteith方法计算[24]，作物潜在蒸腾速率Tp计算式为[25]

Tp=ET0(1-e-KLAI)

(20)

式中LAI——叶面积指数

K——植物灌层辐射衰减系数，向日葵取0.83

2.4 模型参数的率定与检验

2.4.1模型参数的率定

通过土样颗分试验确定试验区的土壤大多为粉壤土，结合 HYDRUS 模型中的 Rosseta 模块得到模型初始土壤水力参数。2018年数据用于模型土壤特征参数的率定，2017年数据用于模型验证，从而确定参数最优解，如表2、3所示。

采用试验区2018年6 月1 日—9 月30日农田观测的分层(25、45、65、85、120 cm)土壤含水率和电导率(EC)实测数据和模拟数据进行对比分析，如图3、4所示，为了评价模型模拟效果，使用平均绝对误差(MAE)、均方根误差(RMSE)2个指标，检验所建立模型的合理性[26]。含水率MAE、RMSE分别为

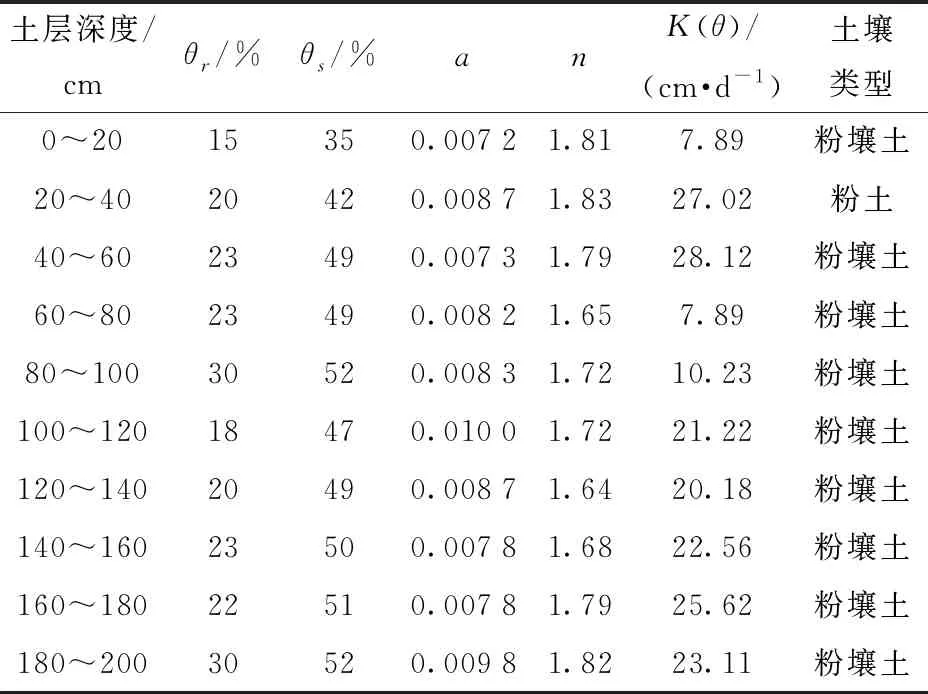
表2 校正后土壤水力参数Tab.2 Calibrated soil hydraulic parameters

表3 校正后的溶质运移参数Tab.3 Calibrated soil solute migration parameters

1.8%～5.3%、2.1%～4.2%，电导率MAE、RMSE分别为0.078～0.22 dS/m、0.065～0.31 dS/m。土壤盐分模拟精度略微差一些，尤其表层土壤盐分的模拟。这主要由于盐分的迁移复杂具有很大的不确定性且表层土壤易受气候条件、人类活动等因素影响。文中所建模型求解可靠。

图3 不同深度土壤含水率模拟值与实测值对比曲线Fig.3 Comparison of measured and fitted soil water content at different soil profiles

图4 不同深度土壤电导率模拟值与实测值对比曲线Fig.4 Comparison of measured and fitted soil salinity at different soil profiles

2.4.2模型参数的检验

采用试验区2017年6月1日—9 月30日的土壤含水率和电导率(EC)实测数据和模拟数据进行验证。

如图5所示，土壤含水率、电导率模拟值与实测值基本分布在1∶1线附近，含水率模拟计算中MAE、RMSE分别为2.3%、4.5%。土壤盐分模拟计算MAE、RMSE分别为0.12、0.33 dS/m。说明实测值与模拟值一致，所构建的模型可行。

3 结果与讨论

3.1 田间最优灌水量设计

灌水定额小，盐分淋洗不充分，根层盐分累积量会增加，作物生长易受盐分胁迫影响[9]。而灌水定额大，虽能促进土壤盐分向根层以下淋洗，但一方面易造成灌后返盐，不易于盐碱地的改良且造成水资源的浪费[27]，另一方面当水分过剩时，向日葵会出现“四低”现象，即叶片的低膨胀、低光合速率、低产量、低根生物量，而且会加速植株的衰老[28-29]。因此，研究不同灌水量对土壤水盐运移的影响，提出有效洗盐、合理用水的灌溉定额，是实现研究区水资源的合理利用及次生盐碱地防治的有效途径。本文通过模型分别对生育期7种灌水量(表4，其中M表示试验区实际灌水定额)下土壤水盐运移进行模拟，确定研究区合理田间灌溉模式，为当地农业生产制定合理灌水制度提供理论依据。

3.1.1不同灌水量对土壤含水率的影响

2018年生育期土壤剖面各层水分变化过程如图6所示，在灌溉期内，不同灌水量下的土壤含水率变化趋势基本一致，灌水量与土壤含水率成正比。从不同土壤深度来看，25、45、65、85、120 cm土壤平均含水率分别为 30%、34%、38%、42%、47%，呈现出土壤含水率随着土壤深度的增大而增加的趋势。表层土壤受灌水影响较大，随着土层深度增加灌溉对土壤含水率的影响逐渐减小，120 cm土壤含水率基本维持稳定。灌后10 d，灌水对土壤水盐运移影响微弱，进入非灌溉期，期间受降雨和蒸发的影响，

表层土壤含水率变动较为频繁且幅度较大，而深层土壤含水率主要受地下水位变化的影响，变化幅度较小。整体来看，由于灌溉和浅埋地下水位，研究时段内耕地土壤含水率均维持在较高水平。

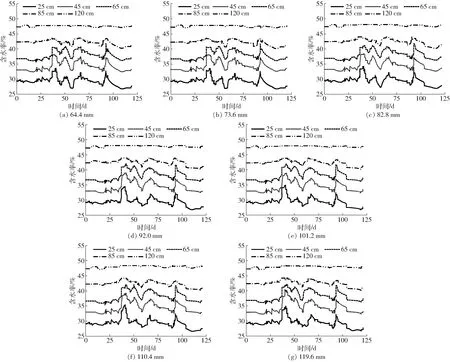
图6 不同灌水量下土壤各土层含水率变化曲线Fig.6 Variation curves of water content in different soil layers under different irrigation amounts

3.1.2土壤含水率变化特征

研究区实测田间持水率为37%，凋萎系数为12%。向日葵主根区通常分布在0～60 cm范围内，以2018年为例，播种期—收获期内主根区(0～60 cm)平均土壤含水率如图7(图中△为灌水影响，○为降雨影响，□为附近灌水影响)所示。由图可知，由于当地地下水位较浅，且受灌水及降雨的影响，各处理土壤含水率在生育期内均高于凋萎系数，生育期土壤大多时间处于水分充足的环境。单就土壤水分来说，不同灌水量均满足向日葵生育期生长所需水量。由此说明，土壤水分并不是限制研究区作物生长发育的主要因素。

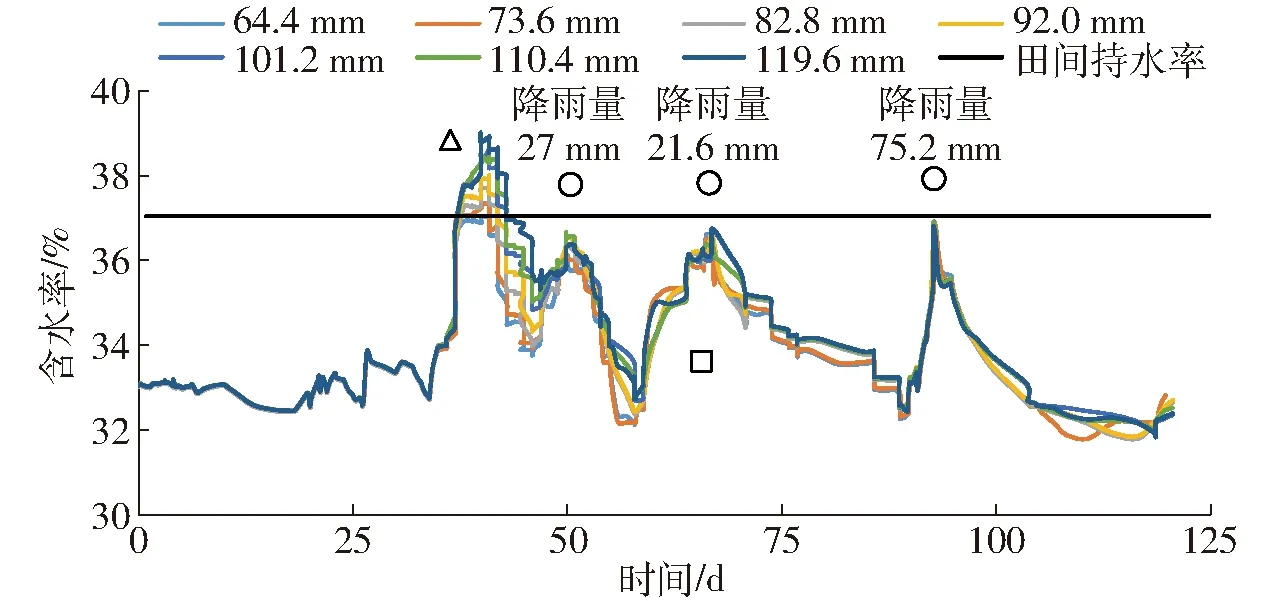
图7 不同灌水量下土壤含水率变化曲线Fig.7 Variation curves of soil water content under different irrigation amounts

3.1.3不同灌水量对土壤含盐量的影响

图8为2018年各灌水处理下向日葵生育期内各土层土壤电导率变化情况。在灌溉期内，土壤盐分变化趋势与水分波动相反，受灌水影响，各处理0～65 cm土层深度盐分明显减小，随着灌水量增大土壤含盐量降低程度越大，但随着灌水量增加至82.8 mm时，这一趋势开始明显减缓。由于灌区排水不畅，淋洗下去的盐分不能及时排出，导致土壤盐分积聚于深层土壤，随着灌水定额的增大，深层土壤盐分累积呈先增加后减少的趋势，各灌水处理导致85 cm土层电导率增至0.99～1.1 dS/m之间。由此可以看出，本设计范围内灌水量对降低主根区(0～60 cm)盐分效果明显。在作物非灌溉期内，除降雨会产生和灌溉对土壤盐分淋洗一样的效果外，由于研究区地下水埋深较浅，土壤水及潜水强烈蒸发，导致盐分又会随着土壤水分向上迁移，再次积累在土壤中。

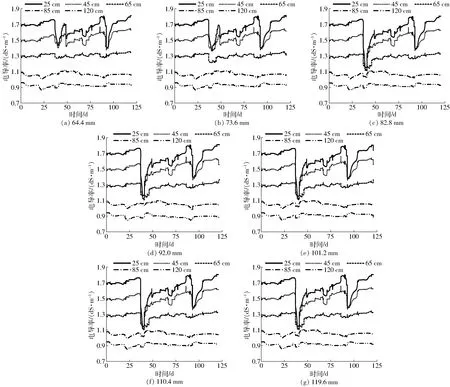
图8 不同灌水量下土壤各土层电导率变化曲线Fig.8 Variation curves of electrical conductivity of different soil layers under different irrigation amounts

3.1.4土壤洗盐率与灌水量的关系

2017、2018年受不同灌水量的影响St随时间变化趋势基本一致(图9)。在灌水后不同时间，St均随着灌水量增大呈增加态势。各灌水量下St均在灌水后3 d达到最大值，而随着时间推移，0～120 cm剖面内St逐渐减小，进入积盐期，这是因为研究区潜水蒸发强烈，土壤水分由下渗转为上移，从而带动盐分向上层集聚。在灌水后10 d，灌水量低于82.8 mm时St均为负值，说明此时只有当灌水量达到82.8 mm以上时才可以达到洗盐效果。

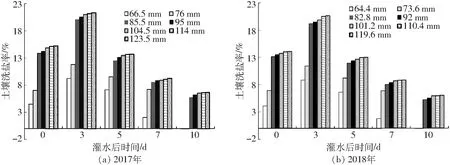
图9 土壤洗盐率与灌溉量的关系Fig.9 Relationship between irrigation amount and wash salt rate

3.1.5边际土壤洗盐率的变化

以试验区0～120 cm土层剖面含盐量随着灌水后时间推移与其灌水前相比的盐分变化量为计算基准，得到S(Zt)的变化如图10所示。可以看出，当灌水量相同时，随着时间推移，S(Zt)呈先增加后减少趋势，在灌水后3 d，2年内灌水量分别为85.5、82.8 mm时，S(Zt)最高，分别较其余灌水处理高8.84%～69.81%和9.34%～68.72%。随着时间推移，各处理S(Zt)均开始降低，但依然表现出灌水量为85.5、82.8 mm高于其他处理。由此表明，灌溉量过小达不到洗盐效果，而灌水量较大洗盐效率降低，造成水资源浪费。

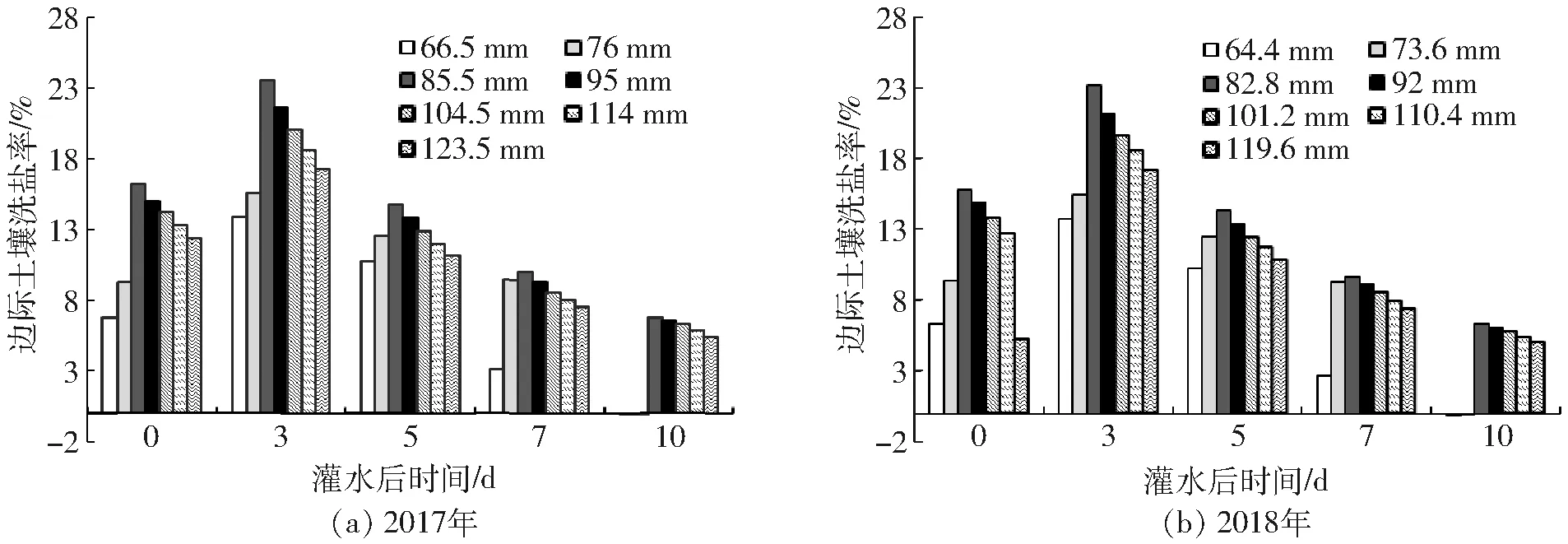
图10 边际土壤洗盐率与灌溉量的关系Fig.10 Relationship between irrigation amount and marginal wash salt rate

3.2 基于土壤水-地下水的水盐调控模式

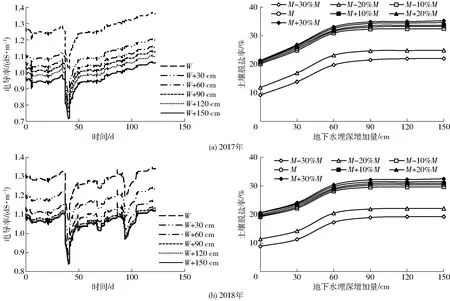
图11 2017年和2018年土壤盐分随不同灌水量及地下水埋深的变化Fig.11 Changes of soil salinity with different irrigation amount and groundwater depths

灌水量和地下水位的调控是对水资源有效利用及土壤盐渍化管理的关键。基于研究区制定的合理灌溉制度和地下水埋深可以有效降低土壤积盐量，防止植物被盐害，同时增加土壤水分利用效率，这对作物的生长与增产具有重要的作用。因此，研究试验区土壤盐分受灌溉和地下水位变化的影响十分必要。本文利用验证后的数值模型，通过改变灌水量和地下水位来进行模拟分析，探寻研究区最优灌水制度及合理的地下水埋深。前人研究表明，土壤积盐程度主要与地下水埋深和矿化度密切相关[30-31]，地下水浅埋区,土壤盐渍化的盐分主要来自于地下水[32],其积盐量与潜水蒸发量密切相关[33]。地下水浅埋区的蒸发量较大,水分强烈向上运移,不仅使地下水中盐分易浓缩,而且加剧了表层土壤积盐[34]，作物易受盐渍化迫害[35-36]。而地下水埋深过大，毛管上升水流很难到达植物根系层，不利于植被的生长与发育[37]。研究发现，当地下水埋深超过2.50 m之后，毛管上升和地下水对作物生长的作用很小[38-39]。也有学者认为，当地下水埋深超过3 m将会对作物生长发育和生态环境产生不利影响[40]。因此设置合理的地下水埋深对于改善土壤水盐状况和植被生长环境起着关键作用。前期研究表明，向日葵由于在生育期内只进行一次灌水，因此，本研究基于不同灌水量情景进一步对地下水埋深情景进行预测分析。研究区地下水埋深较浅(平均为100.72 cm)，故基于试验区地下水埋深的基础上分别增加30、60、90、120、150 cm进行数值模拟。2017、2018年不同灌水处理下土壤盐分对地下水埋深变动的响应规律趋于一致(图11，图中W为试验区实际地下水埋深)，结果表明，不同灌水量下，较浅的地下水埋深对土壤盐分调控能力有限，随着地下水埋深增大土壤洗盐率逐渐增加，但当地下水埋深到达160.72 cm时，对土壤盐分调控趋于平缓，并且考虑到地下水浅埋深为作物提供水分的作用，地下水埋深不能过深。在同一地下水埋深条件下，随着灌水量增加土壤洗盐率增大，当灌水量增至M-10%M时，再继续增大灌水量对土壤盐分淋洗效果不明显。以2018年的M-10%M灌水量为例，分析不同地下水埋深对土壤盐分变化的影响发现，当地下水埋深从100.72 cm增加到130.72、160.72、190.72、220.72、250.72 cm时，土壤洗盐率(灌水后3 d盐分减少量与灌水前含盐量之比)分别增加了23.44%、53.45%、60.31%、60.85%、61.05%。因此，综合对水资源利用、生态环境方面的考虑，研究区适宜的灌水量及地下水埋深分别为82.8～85.5 mm及160.72 cm。