GLOBAL SIMPLE WAVE SOLUTIONS TO A KIND OF TWO DIMENSIONAL HYPERBOLIC SYSTEM OF CONSERVATION LAWS∗

Jianli LIU(刘见礼)Jie XUE(薛杰)

Department of Mathematics,Shanghai University,Shanghai 200444,China

E-mail:jlliu@shu.edu.cn;jiexue@163.com

Abstract This paper is concerned with the simple waves of a kind of two dimensional hyperbolic system of conservation laws,which can be obtained from the two dimensional relativistic membrane equation in Minkowski space.Using wave decomposition method,we get that a flow adjacent to a nonconstant state can be a global simple wave.Furthermore,the flow is covered by three families of characteristics,in which the first family of characteristics is straight and the others are curved,which is different to the almost related results.

Key words global simple wave solutions;conservation laws;relativistic membrane equation

1 Introduction

In this paper,we will try to find the simple wave solutions of a kind of two dimensional hyperbolic system of conservation laws as following

where∆=1+u2+v2−w2>0,which can be obtained from the two dimensional relativistic membrane equation in Minkowski space

where ∇ =(∂x,∂y).Relativistic membrane equation is very important on Lorentz geometry and particle physics.For one dimensional case,Kong,Zhang and Zhou studied dynamics of a relativistic string in Minkowski space R1+n[1].He and Kong studied and obtained spherical symmetric solutions for the motion of relativistic membranes in curved spacetime[2].For two dimensional system,Hoppe gave the classical solutions of the equation of motion of a relativistic membrane[3].Wang and Wei got the global,smooth solution with a class of large initial data for the relativistic membrane equation[4].The other related results can also be found in[5–7].

As is well known,a flow in a region is called simple wave if it depends on a single parameter.It plays an important role in the theories of gas dynamics and fl uid mechanics.Moreover,it can be used to describe and build up solutions of flow problems[8–14].Courant and Friedrichs showed that a flow in a region adjacent to a constant state is always a simple wave[8].For the system of two dimensional steady isentropic irrotational Euler system,a signifi cant property is that a nonconstant state of flow adjacent to a constant state is always a simple wave by Riemann invariants[8].Using the characteristic decomposition method,Li,Zhang and Zheng proved that any wave adjacent to a constant state is a simple wave for the compressible Euler system[10].And the characteristic decomposition as a powerful tool for building patches of global smooth solutions was also used in[12,13,15–18].Recently,Hu and Sheng extended Courant and Friedrich’s well-known result for reducible equations to 2 × 2 non-reducible equations[19,20].Chen and Sheng established that the wave adjacent to a constant state must be a simple wave to the two dimensional compressible magnetohydrodynamics system for a polytropic Van der Waals gas and a polytropic perfect gas[21].Lai and Sheng constructed the expansion or compression simple wave flow for two-dimensional compressible pseudo-steady Euler system[22].For the case that a flow adjacent to a nonconstant state,Chen and Zhou proved the local existence of simple wave solutions for compressible full Euler system[14].

In this paper,we want to consider a flow adjacent to a nonconstant state for the two dimensional hyperbolic system of conservation laws(1.1)in self-similar coordinates(ξ,η)=()as following

Therefore,we can obtain the eigenvalues as

and

Proposition 1.1System(1.2)is hyperbolic if ξ2+ η2− 1>0.

In fact,we can rewrite the system(1.4)as

where

Rewriting the above equation,we have

Noting ∆ >0,we know τ>0 if ξ2+η2−1>0,i.e.,λ1,2exits if ξ2+η2−1>0.Thus,we can obtain the conclusion of Proposition 1.1.

Furthermore,we can get the generalized left eigenvectors and the generalized right eigenvectors corresponding to the eigenvalues λ0,λ1and λ2are

and

Then we can get the following result.

Theorem 1.2For system(1.2)in the hyperbolic region,the flow adjacent to a nonconstant state can be a global simple wave in which the variables(u,v,w)are constant along a family of characteristics.Furthermore,the characteristic contains the curved case.

Remark 1.3Using our method,we can also get the flow adjacent to a constant state is the global simple wave,which is consistent with the famous result.

Remark 1.4Unlike the general result that the flow is covered by a family of straight characteristics,we get the flow covered by a family of straight characteristics and two families of curved characteristics.

2 Proof of Main Result

In this section,we first give the wave decomposition which plays important role in our main result.System(1.2)can be written as the first order quasilinear system

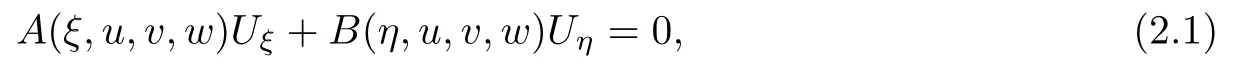
where U=(u,v,w)Tand

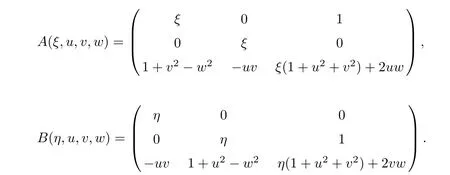
Obviously,system(2.1)is a non-reducible quasilinear system.Using the simple computation,the characteristic equation of system(2.1)is

We can also get the characteristic form of the self-similar system(2.1)

Therefore,we denote the left eigenvectors of system(2.2)are

Then

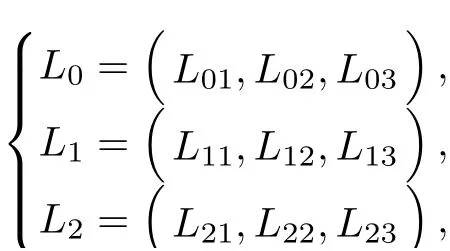
where

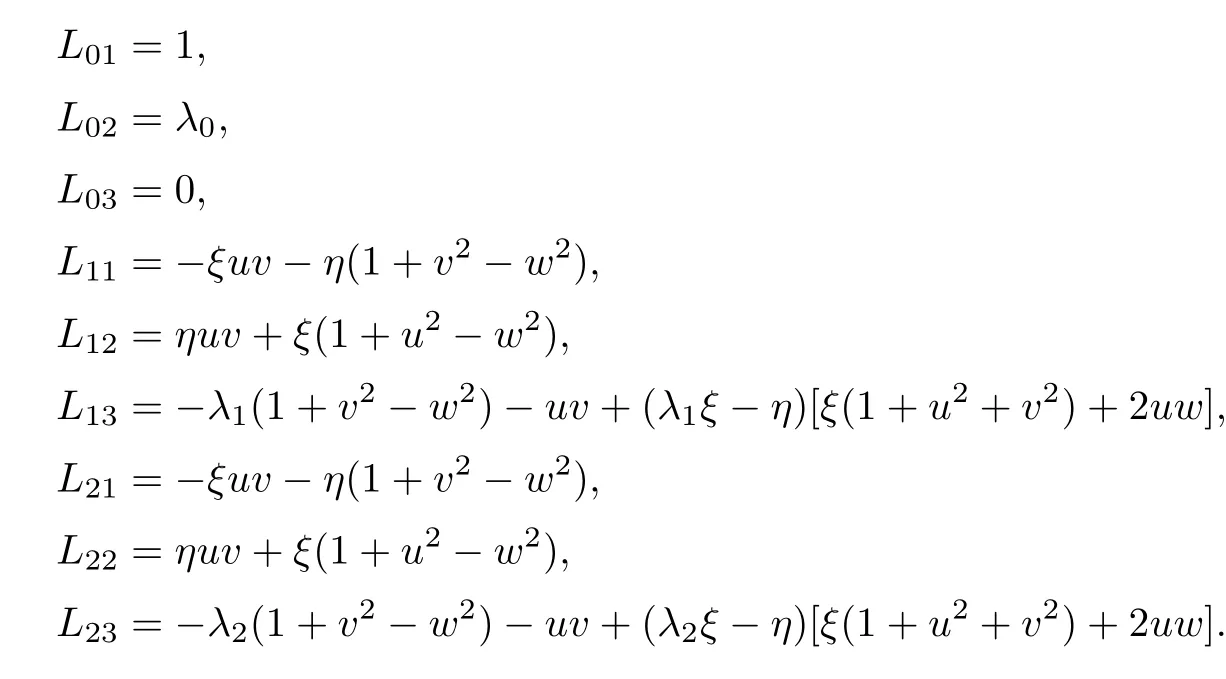
Furthermore,we assume that

where δijstands for the Kronecker’s symbol.Thus we can get the corresponding right eigenvectors

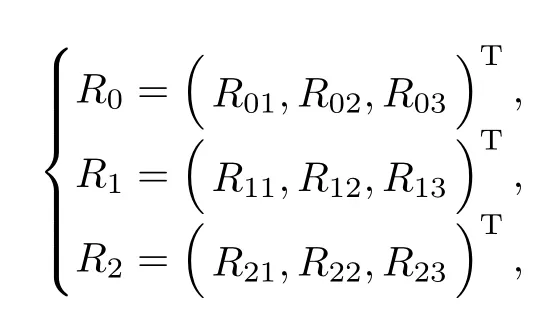
where

and

Denoting

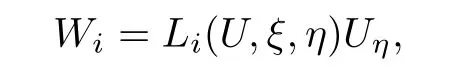
we have

It is easy to recast system(2.1)as

Differentiating system(2.5)with respect to η,we can get

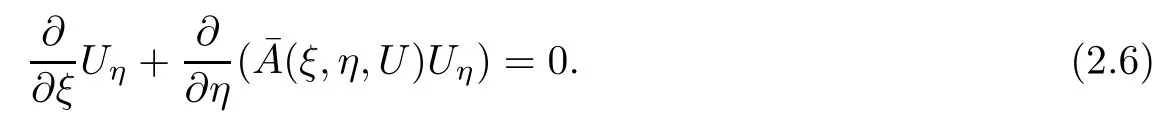
By(2.4)and(2.6),we can obtain

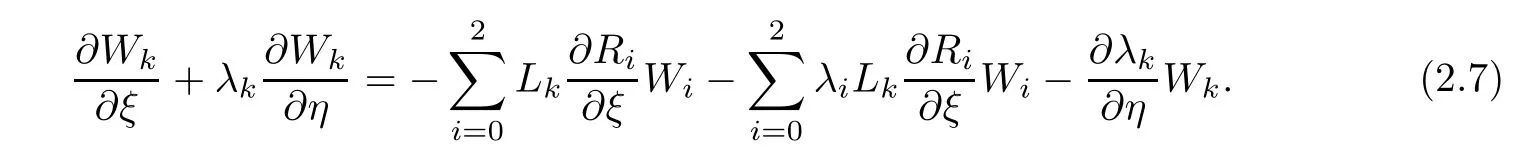
In the following,we will estimate the right side hand of(2.7)term by term

where Ri,ξdenotes R(U,ξ,η)differentiates with respect to variable ξ.Then

Noting

Thus,we can get

Next,we will give the proof of main result with three different cases.

Case 1We chooseBy(2.8),we have

Because of(2.3),along the k-th direction of characteristic,we have

Through a series of computation,we have

where

Then we can obtain

Substituting(2.10)–(2.12)into(2.9)respectively,we can get

Thus we can get that(W0,W1,W2)satis fies system(2.5)rewritten from system(2.1)and keeps the initial state along corresponding characteristic line,hence it determines a family of global simple wave solution.

Furthermore,noting the property of simple waves,we can get

Noting(2.5)and differentiating U(ξ,η)along the λ0characteristic,we obtain

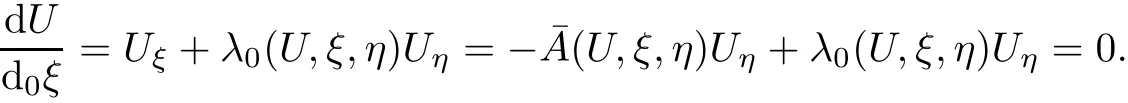
Therefore U=(u(ξ,η),v(ξ,η),w(ξ,η)keep constants on fixed λ0-th characteristic.Moreover,by(1.3)we can get

Hence we can prove

Therefore,using the wave decomposition,we prove that there are global simple wave solutions of the two dimensional hyperbolic system of conservation laws which is determined by(W0,W1,W2).Moreover,the global simple wave flow region is covered by a family of straight characteristics λ0and along each of these lines U=(u,v,w)remain constants.

Case 2By(2.8)and choosing,we have

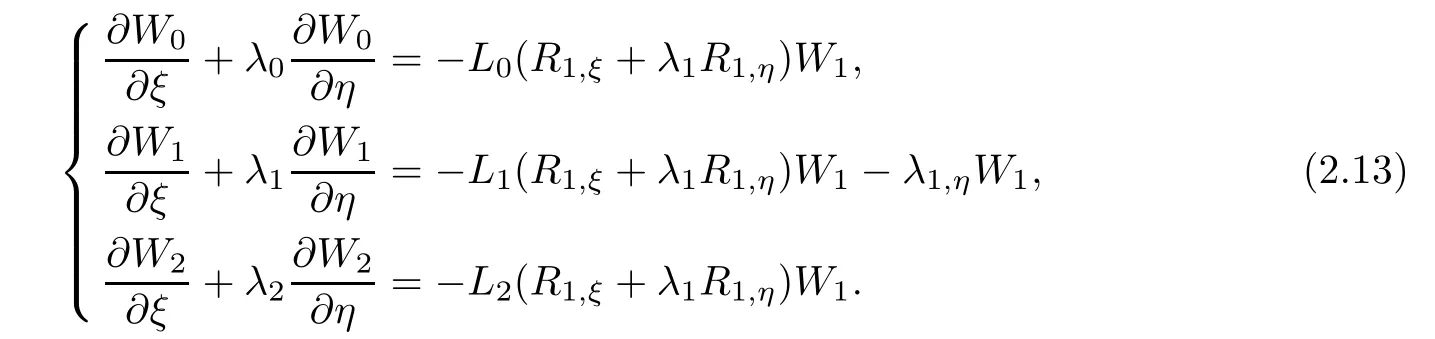
Differentiating the left eigenvectors,we can get

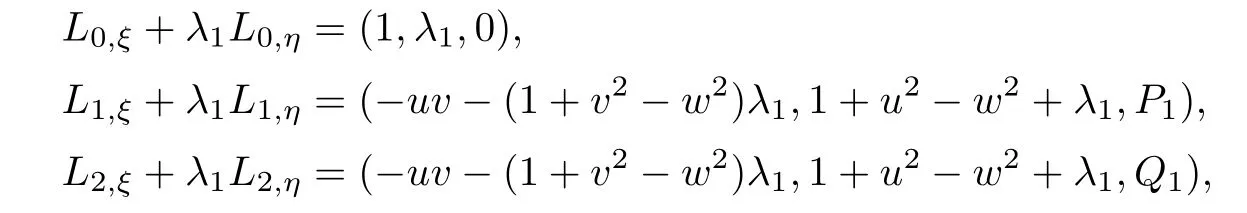
where

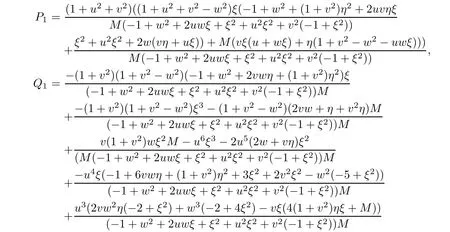
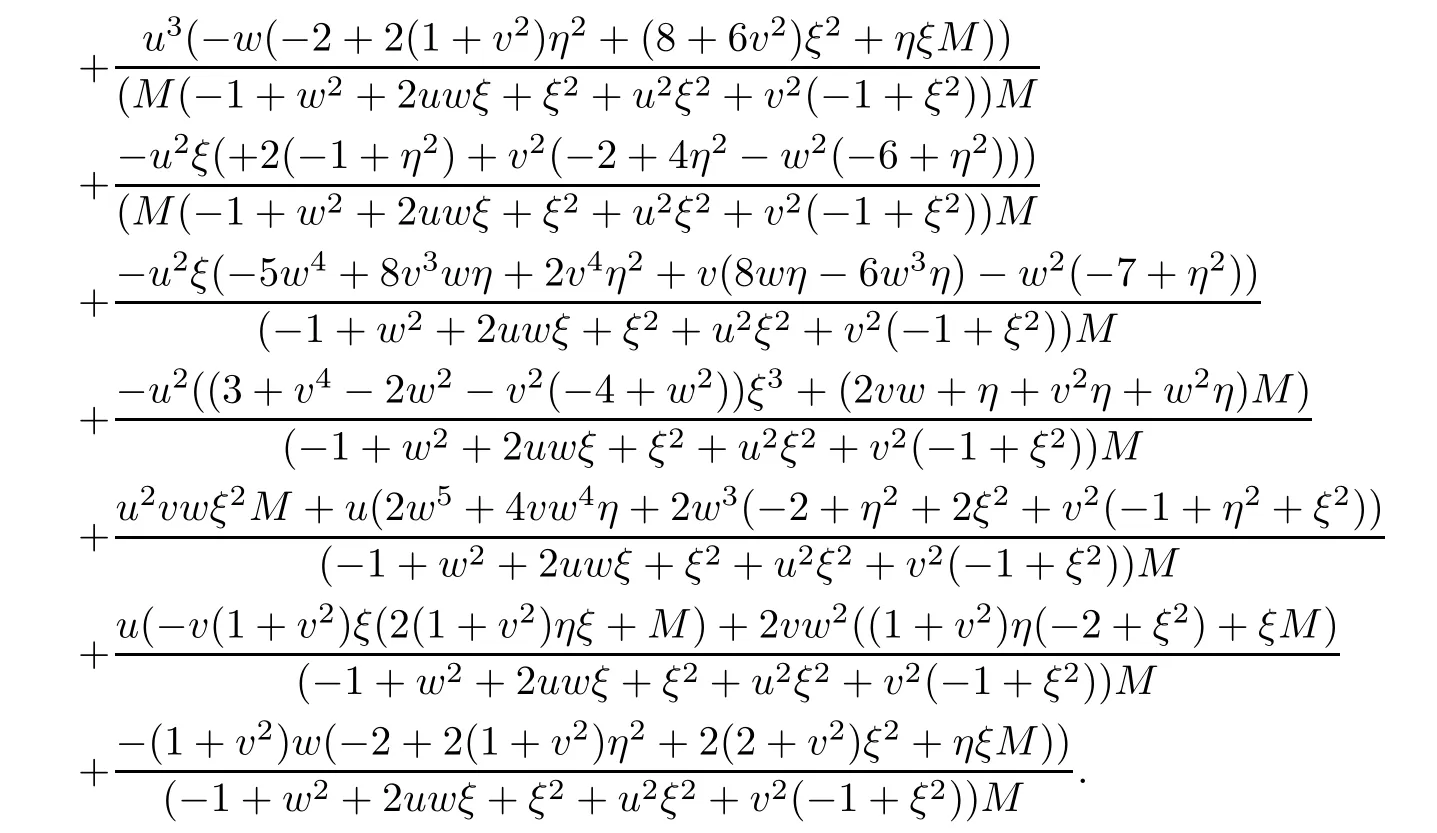
Then,we can obtain

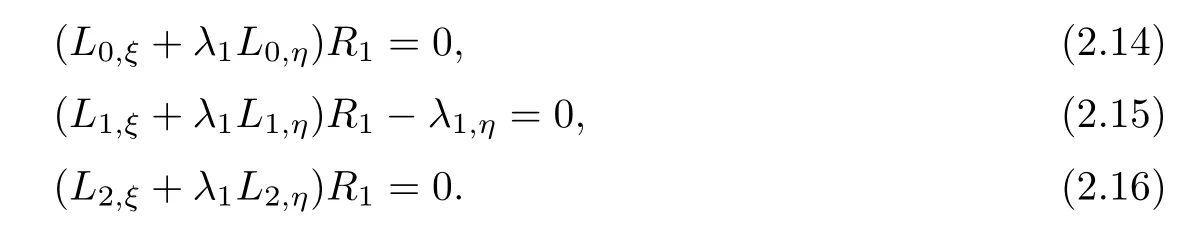
Substituting(2.14)–(2.16)into(2.13),we can get

Hence we have obtained that(W0,W1,W2)keeps the initial state along corresponding characteristic line and determines the λ1-th global simple wave solutions of the kind of two dimensional hyperbolic system of conservation laws with

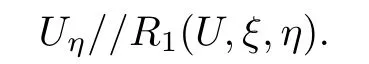
Furthermore,we have

It implies that the solutions U=(u,v,w)along the λ1-th characteristic line keep constants.

Finally,we get the result that characteristics λ1are curved which is different to the previous results[8,10,14,19–21].To prove that,we recall the characteristic equation of λ1as

where

Differentiating system(2.18)with respect to ξ,η respectively,we can easily find

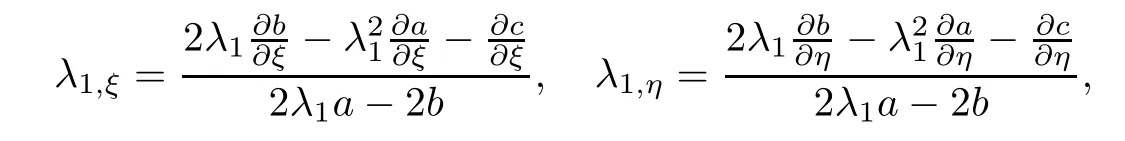
where

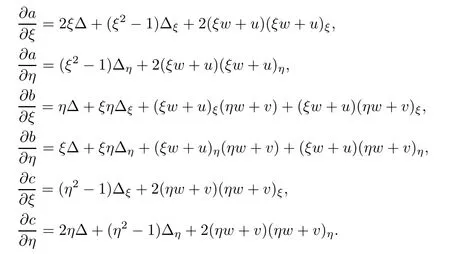
Noting(2.17),we have

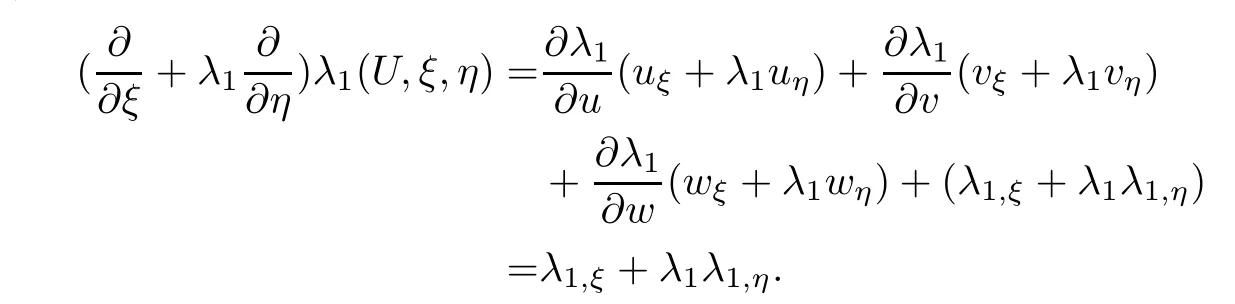
Through the complex computation,we find

Then,we can rewrite the above equation as

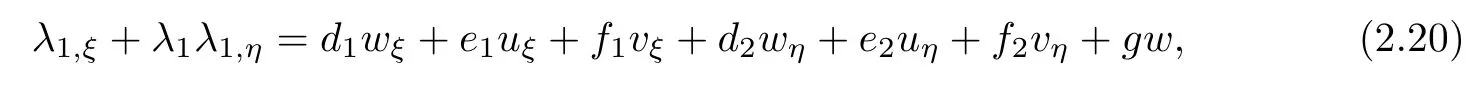
where

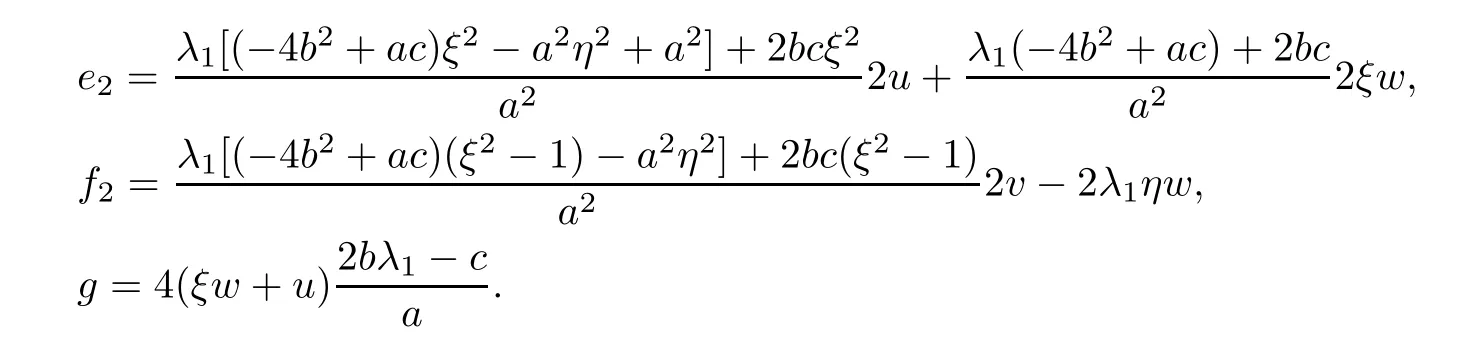
And we know the terms of system(1.2)are all derivative terms,including wξ,uξ,vξ,wη,uη,vη.In fact,we can obtain the coefficient of w as following

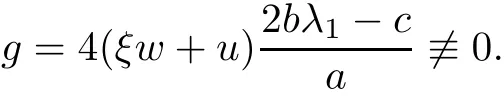
Therefore,we get

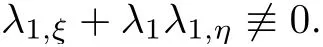
Thus we can obtain the characteristics x=x1(t):=λ1are curved.

Case 3By the same method as Case 2,we can get the conclusion of this case.When the initial data satis fies,==0,we can also obtain global simple wave solutions of the two dimensional hyperbolic system of conservation laws.Moreover,we find the global simple wave flow region is covered by the curved characteristics

Remark 2.1Noting(2.8),we can also get that when the initial data satis fies===0,there are global simple wave solutions of the two dimensional hyperbolic system of conservation laws.

In conclusion,we get global simple wave solutions of the two dimensional hyperbolic system of conservation laws under three different cases of initial data.The global simple wave flow region corresponding to each case is covered by characteristics λ0,λ1and λ2,respectively.Furthermore,λ0characteristics are straight and λ1,2characteristics are curved.

AcknowledgementsThe authors would like to thank Prof.Wancheng Sheng for helpful discussion and encouragement.