HERMITIAN-EINSTEIN METRICS FOR HIGGS BUNDLES OVER COMPLETE HERMITIAN MANIFOLDS∗
2020-04-27DebinLIU刘德斌
Debin LIU(刘德斌)
School of Mathematical Sciences,University of Science and Technology of China,Hefei 230026,China
E-mail:liudebin@mail.ustc.edu.cn
Pan ZHANG(张攀)†
School of Mathematics,Sun Yat-sen University,Guangzhou 510275,China
E-mail:zhangpan5@mail.sysu.edu.cn
Abstract In this paper,we solve the Dirichlet problem for the Hermitian-Einstein equations on Higgs bundles over compact Hermitian manifolds.Then we prove the existence of the Hermitian-Einstein metrics on Higgs bundles over a class of complete Hermitian manifolds.
Key words Higgs bundles;complete Hermitian manifolds;Hermitian-Einstein metric
1 Introduction
Let(M,g)be a Hermitian manifold and the corresponding Kähler form is denoted by ω .A Higgs bundle(E,,θ)over M is a holomorphic vector bundle(E,)coupled with a 1-form θ∈Ω1,0(M,End(E))satisfying=0 and θ∧θ=0,which is called the Higgs field.Higgs bundle was introduced by Hitchin[10]in his study of self-dual equations on a Riemann surface.It has rich structures and plays an important role in many areas including gauge theory,Kähler and hyper-Kähler geometry,group representations and nonabelian Hodge theory.
For any given Hermitian metric H on a Higgs bundle E,we de fine its Hitchin-Simpson connection[26]to be
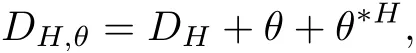
where DHis the Chern connection with respect to H and,and θ∗His the adjoint with respect to H.The curvature of this connection is given by
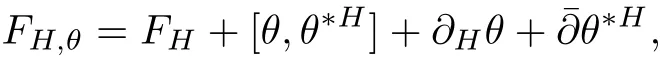
where FHis the curvature of the Chern connection DHand∂His the(1,0)part of DH.We say H is a Hermitian-Einstein metric,if its curvature FH,θsatis fies the Einstein condition:
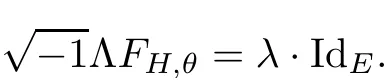
The celebrated Donaldson-Uhlernbeck-Yau theorem states that holomorphic vector bundles over compact Kähler manifolds admit Hermitian-Einstein metrics if they are stable.It was proved by Narasimhan and Seshadri[22]for compact Riemann surface,by Donaldson[7]for algebraic manifolds and by Uhlenbeck-Yau[29]for general compact Kähler manifolds.The inverse problem is that a holomorphic bundle admitting such a metric must be polystable(that is a direct sum of stable bundles with the same slope).And this was proved by Kobayashi[12]and L¨ubke[19]independently.This is the so-called Hitchin-Kobayashi correspondence for holomorphic vector bundles over compact Kähler manifolds.There were many interesting generalized Hitchin-Kobayashi correspondences(see the References[1–6,10,11,13–16,20,21,25,30,32],etc.).In the meanwhile,the Dirichlet problem was solved by Donaldson[8]for Hermitian-Einstein metrics over compact Kähler manifolds with non-empty boundary,and many interesting applications were addressed.Li and Zhang[18]generalized Donaldson’s result to the general Hermitian manifolds and considered a class of vortex equations,which generalize the well-known Hermitian-Einstein equations.As for the non-compact case,Ni and Ren[24]proved that a holomorphic vector bundle over a complete non-compact Kähler manifold with a spectral gap admits a Hermitian-Einstein metric if it admits a metric whose failure to be Hermitian-Einstein is in Lpfor p>1.Ni[23]also showed that the same conclusion holds,for example,if the Kähler manifold satis fies a L2-Sobolev inequality,or if it is non-parabolic(i.e.,admits a positive Green’s function).Later,Zhang[33]studied the existence of Hermitian-Einstein metrics for holomorphic vector bundles over complete Hermitian manifolds.At the same time,he[34]also proved the existence of Hermitian Yang-Mills-Higgs metrics for holomorphic vector bundles on a class of complete Kähler manifolds.
When it comes to the Higgs bundles,Hitchin[10]and Simpson[26]obtained a Higgs bundle version of Donaldson-Unlenbeck-Yau theorem,i.e.,they proved that a Higgs bundle admits a Hermitian-Einstein metric if and only if it is Higgs polystable.Simpson[26]also considered some non-compact Kähler cases.He introduced the concept of analytic stability for Higgs bundles and proved that the analytic stability implies the existence of Hermitian-Einstein metrics.Recently,Zhang et al.[31]showed the existence of Hermitian-Einstein metrics of analytic stable Higgs bundles over complete non-compact Gauduchon manifolds.
In this paper,we skip the stability conditions,and assume that the spectrum of a holomorphic Laplace operator has a positive lower bound(see[24]and[33])or the holomorphic Laplace operator satis fies the L2-Sobolev inequality(see[23]),we study the existence of Hermitian-Einstein metrics of Higgs bundles over complete Hermitian manifolds.More precisely,we will prove the following theorem.
Theorem 1.1Let(M,g)be a complete Hermitian manifold of complex dimension m,and(E,,θ)be a Higgs bundle over M,with an initial Hermitian metric H0.
1)Assume that the holomorphic operatorhas positive first eigenvalue(M)and thatfor some p ≥ 2 and real number λ.Then there exists a Hermitian-Einstein metric H on E.
This paper is organized as follows.In Section 2,we give some estimates and preliminaries which will be used in the proof of the theorem.In Section 3,using the Hermitian-Einstein flow,we solve the Dirichlet problem for the Hermitian-Einstein equations over a compact Hermitian manifold.In Section 4,we prove the long-time existence of the Hermitian-Einstein flow over a complete Hermitian manifold.At last,we complete the proof of the main theorem in Section 5.
2 Preliminary Results
Let(M,g)be a compact Hermitian manifold,and(E,¯∂,θ)be a rank r Higgs bundle over M with an initial Hermitian metric H0.Denote by ω the Kähler form,and de fine the operator Λ as the contraction with ω,i.e.,for α ∈ Ω1,1(M,E),one has Λα =hα,ωi.For any local complex coordinatein M,we can de fine the holomorphic Laplace operator for functions as
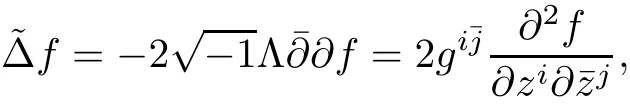
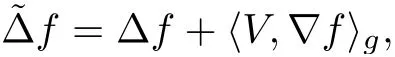
where V is a well-de fined vector fields on M.The holomorphic Laplace operatorcoincides with the usual Beltrami-Laplace operator if and only if the base manifold(M,g)is Kähler.
Given any Hermitian metric H on E,since the bundle E is holomorphic with the holomorphic structure,there is a unique corresponding connection AHwhich is called the Chern connection.Under a holomorphic local frame{eα},we can express the metric H as a positive de fined matrix()1≤α,β≤r,where=H(eα,eβ).For simplicity we will still denote it by H.Then locally the Chern connection AHand its curvature form FHcan be written as

Now consider two Hermitian metrics H and K on E.Set h=K−1H ∈Ω0(M,End(E)).It is easy to check that h is positive de fined and self-adjoint with respect to both H and K.Then by a direct calculation we have
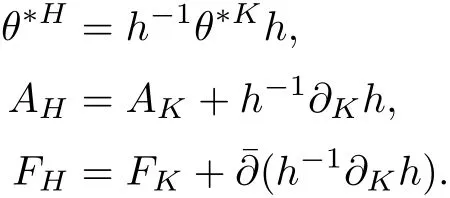
Next,we turn to a family of Hermitian metrics H(t)on E with an initial metric H(0)=H0.We will follow the classical heat flow method to deduce the existence of Hermitian-Einstein metric.Actually,we consider the following Hermitian-Einstein flow
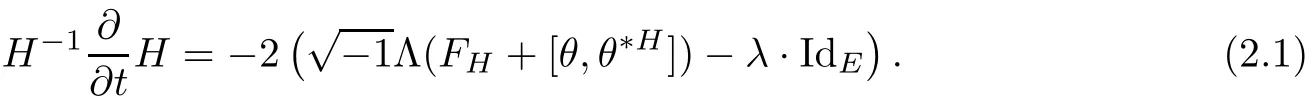
Taking a local holomorphic frame{eα}of E and local complex coordinates{zi}of M,the above flow can be written as

We will see later the following proposition plays an important role in our discussion.
Proposition 2.1Let H(t)be a solution of the flow(2.1),then

ProofFor simplicity,setThen by a direct calculation,we have

and
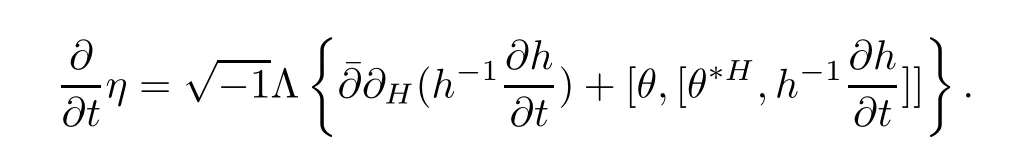
Hence
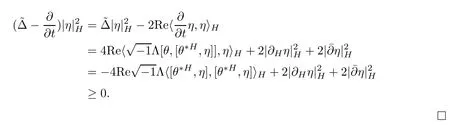
Now we recall the Donaldson’s distance on the space of Hermitian metrics as follows.
De finition 2.2For any two Hermitian metrics H and K on the bundle E,we de fine
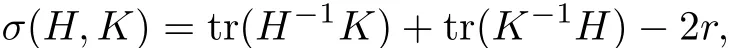
where r=rank(E).
If we choose a local frame to diagonalize H−1K to be diag(λ1,···,λr),then
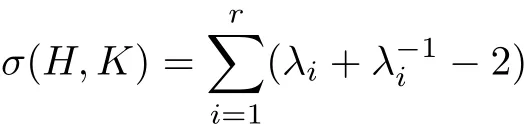
from which we can see that σ≥0 with equality if and only if H=K.Let d be the Riemannian distance function on the metric space,then
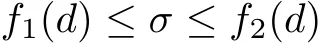
holds for some monotone functions f1and f2.So we can conclude from this inequality that a sequence of metrics Hiconverges to some H in C0-topology if and only if
For later use,we need the following lemma.
Lemma 2.3
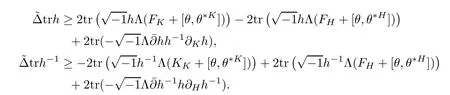
ProofIt is easy to check that
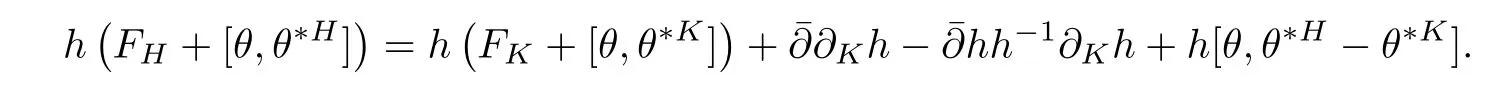

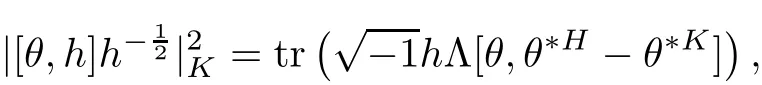
On the other hand,it is easy to check that tris nonnegative,by doing calculation locally[27].Hence we have the following proposition.
Proposition 2.4Let H,K be two Hermitian-Einstein metrics,then

Next,instead of considering H,K as Hermitian-Einstein metrics,we assume H=H(t),K=K(t)to be two solutions of the Hermitian-Einstein flow(2.1)with the same initial value H0.Similar to Proposition 2.4,we prove the following proposition.
Proposition 2.5

ProofSet h(t)=K(t)−1H(t).Notice that
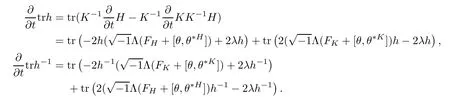
These two identities together with Lemma 2.3 show that
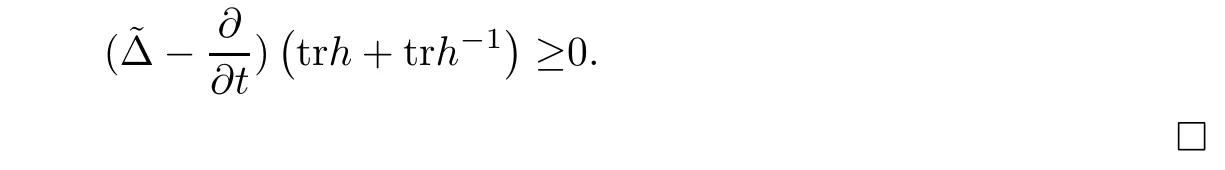
For further discussion,we prove the following.
Proposition 2.6Let H(x,t)be a solution of the Hermitian-Einstein flow with the initial metric H0and set h=H,then
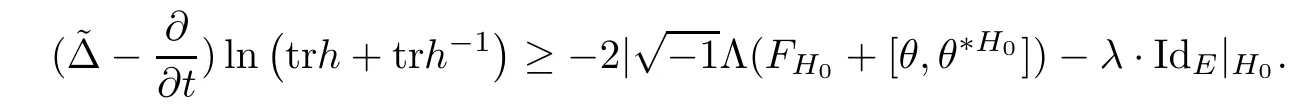
ProofThe proof is quite straightforward.First notice that
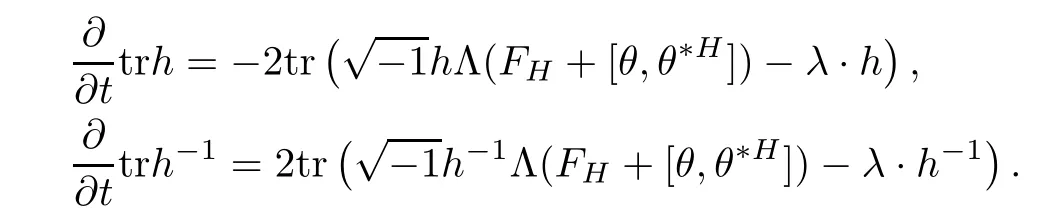
And following the same argument as in[27],one can show that
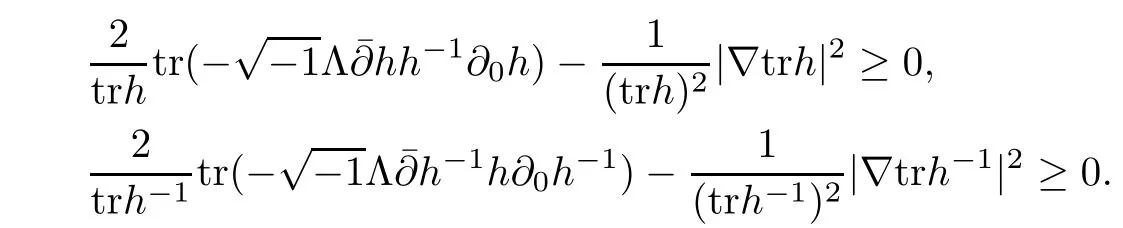
Set d=trh+trh−1,then from the above two inequalities,we can get
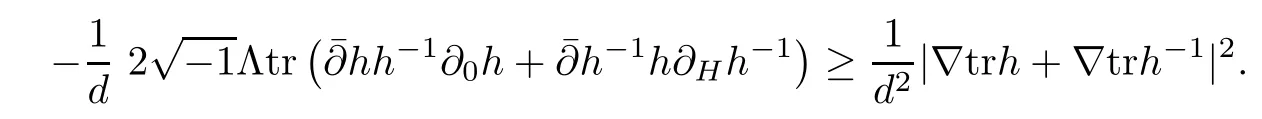
Using the above discussion and Lemma 2.3,we can deduce that
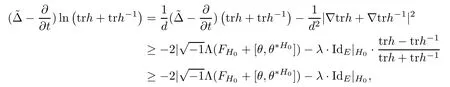
where the last inequality follows from the fact that
Proceeding by a similar argument,we have
Corollary 2.7Let H be a Hermitian-Einstein metric and H0be the initial Hermitian metric.Let h=H,then
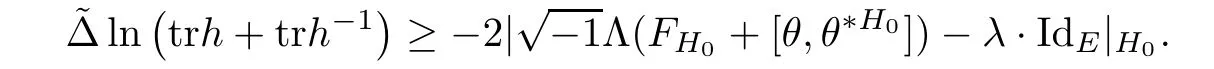
3 Over Compact Manifolds
In this section our primary purpose is to solve the Dirichlet problem for the Hermitian-Einstein flow over a compact manifold.Speci fi cally,when the base manifold M is closed,we consider the following problem

And when M is a compact manifold with a non-empty smooth boundary∂M,for any given initial metric ϕ over ∂M we instead consider the following boundary value problem

One can easily check that the equation in(3.1)is non-linear,strictly parabolic.So we get the short-time existence from the standard parabolic PDE theory[9].
Theorem 3.1For sufficiently small ε>0,problems(3.1)and(3.2)have a smooth solution de fined for 0≤ t< ε.
Next,following a standard argument,we can show the long-time existence of(3.1)and(3.2).
Lemma 3.2Suppose that a smooth solution Htto(3.1)or(3.2)is de fined for 0≤t Then Htconverges in C0topology to some continuous non-degenerate metric HTas t→T. ProofIn order to prove the convergence,it suffices to show that,given any ε>0,we can find δ>0 such that And this can be easily seen from the continuity at t=0 combining with Proposition 2.5 and the maximum principle. So,it remains to show HTis non-degenerate.By Proposition 2.1,we know that where C=C(H0)is a uniform constant.By a direct calculation we have And similarly Then we can conclude that σ(H,H0)is uniformly bounded on M × [0,T),which implies that HTis non-degenerate. For further consideration,we need the following lemma. Lemma 3.3Suppose M is a closed Hermitian manifold without boundary(compact with non-empty boundary).Let H(t)for 0≤t 1)H(t)converges in C0topology to some continuous metric HTas t→T, 2)supM|ΛFH|H0is uniformly bounded for t Then H(t)is bounded in C1,and also bounded in(for any 1 Since the proof is exactly the same as that in[7]and[26],we omit it here. Theorem 3.4Problems(3.1)and(3.2)have a unique solution H(t)which exists for 0≤t<∞. ProofTheorem 3.1 guarantees that a solution exists for a short time.Then we suppose that there is a solution H(t)existing for 0≤t Finally,since we have proved the long-time existence of the Dirichlet problem(3.2),it remains for us to show that the solution H(t)converges to a metric H∞as the time t approaches to the in fi nity,and that the limit H∞is Hermitian-Einstein. Suppose H(t)is a solution to(3.2)for 0≤t<∞.As in the previous section we still setFrom Proposition 2.1 and the fact thatholds for any section α of End(E),we have Next,according to Proposition 1.8 of Chapter 5 in[28],the following Dirichlet problem is solvable Therefore the maximum principle implies that for any y∈M and 0≤t<∞. Let 0≤t1≤t<∞,=H−1(x,t1)H(x,t).Obviously¯h satis fies Then we have Integrating it over[t1,t]gives From(3.6)and(3.7),we have that H(t)converges in the C0topology to some continuous metric H∞as t−→ +∞.Hence using Lemma 3.3 again we know that H(t)has uniform C1andbounds.This together with the fact thatis uniformly bounded and the standard elliptic regularity arguments shows that,by passing to a subsequence if necessary,H(t)→H∞in C∞topology.And from(3.6)we have i.e.,H∞is the desired Hermitian-Einstein metric satisfying the Dirichlet boundary condition.Since for any given initial Hermitian metric ϕ over boundary ∂M one can construct a Hermitian metric H0over M with H0|∂M= ϕ by choosing a proper partition of unity,we have eventually proved the following theorem. Theorem 3.5Suppose(M,g)is a compact Hermitian manifold with non-empty boundary∂M and(E,,θ)is a Higgs bundle over M.Then for any Hermitian metric ϕ on restriction of E to∂M there is a unique Hermitian metric H on E such that Let M be a complete non-compact Hermitian manifold without boundary,in which case we will still call it complete for short,and E be a rank r Higgs bundle over M with an initial Hermitian metric H0.Suppose the curvature of AH0satis fiesIdE|H0≤C0for some positive constant C0.What we want to prove is the existence of the long time solution to the Hermitian-Einstein flow over M starting at H0. It is well known that for any topological manifold M we can always find a compact exhaustion sequence,i.e.,a countable collection of compact subsetsof M which satis fiesΩi⊂ Ωi+1andΩi=M.Moreover,if the manifold is smooth we can further assume that∂Ωiis smooth for each i.Now for such an exhaustion,by our discussion in Section 3 we can find Hermitian metrics H(x,t)on E|Ωifor each i,which solve the following problems Notice here we use H0as both the initial metric with respect to t and the boundary metric.So Proposition 2.1 together with the maximum principle shows that As before we set hi=Hi.Then through a simple calculation(as is shown in the proof of Lemma 3.2),we can see that Integrating along time direction from 0 to T,we have This immediately implies and In particular,for any compact subset K we can choose i large enough so that K⊂Ωi,then we get the following C0-estimate Without loss of generality,we can assume that K=Bo(R),here K=Bo(R)denotes the geodesic ball of radius R center at a fixed point o∈M.We want to show that,by passing to a subsequence if necessary,{Hi}converges uniformly to a Hermitian metric H∞(x,t)over Bo(R)×[0,T/2].By Lemma 2.3,we have Hence using(4.3)and(4.4),we can get the following estimate where C3is a uniform constant depending only on C0,T,R and V.Since(4.7)gives the uniform C0-estimate for hiand notice thatis also uniformly bounded,(4.8)implies that hiis uniformly bounded in(Bo(2R)×[0,T]).From Sobolev embedding theorem we know that(Bo(2R)×[0,T])can be compactly embedded into L2(Bo(2R)×[0,T]).So by passing to a subsequence if necessary,we conclude that hi,and hence Hi,converges in L2(Bo(2R)×[0,T]). This implies that given any ε>0,we have for j,k sufficiently large.In order to show the uniform convergence,we need the following mean-value type inequality. Lemma 4.1(see[33,Lemma 5.2])Let M be an m-dimensional complete non-compact Hermitian manifold without boundary,and Bo(2R)be a geodesic ball,centered at o∈M of radius 2R.Suppose that f(x,t)is a non-negative function satisfying over Bo(2R)×[0,T].Let−K ≤0 be the lower bound of the Ricci curvature of Bo(2R).Then for any p>0,there exist positive constant C′and C′′depending only on C,m,R,K,p,T and V such that Now let f(x,t)=σ2(Hj(x,t),Hk(x,t)).Obviously fsatis fies(4.10)with C=0.Then by Lemma 4.1,(4.9)and the fact that Hj=Hkat t=0 gives here C4is a positive constant depending only on C0,R,T and the bound of the sectional curvature on Bo(2R).And this implies that,by passing to a subsequence if necessary,Hiconverges uniformly to a continuous Hermitian metric H∞over Bo(R)×[0,T/2]. Finally,we want to use the above C0-estimate to deduce a C1-estimate over any compact subset K.We will follow Donaldson[8]and Zhang[33].For any point x∈Bo(2R)we can choose a coordinate ball Bx(R′)centered at p small enough such that E can be locally trivialized over it.Let{yj}be a real coordinate on Bx(R′)and denoteΩ0(M,End(E)).Then we have the following. Proposition 4.2ρlis de fined as above,then ProofFrom(4.1),we know Hisatis fies For now for the sake of calculation convenience,we omit the subscript i and l and denote Hi,ρlto be H,ρ respectively.Then by considering a one-parameter family of solutions obtained by translating in the direction ofone can check that where As is shown in the proof of Proposition 2.1,one can check that By direct calculation,we have and one can easily check that Then combining those calculations together shows that Then this proposition together with Lemma 4.1 and(4.8)gives where C5is a positive constant independently on i.Moreover,for the Hermitian metric g there exist constants C6and C7such that holds over Bx(R′).Hence we have From this and(4.12)we can fi nally conclude that there exists a positive constant C8which is independently of i such that Since x is arbitrary,we can see that Hihas a uniform C1-bound over Bo(R)×[0,T/4].Since we have derive the C0and C1estimates,the standard parabolic theory is enough to show the global convergence of Hi,which is Theorem 4.3Let(M,g)be a complete non-compact Hermitian manifold without boundary,and(E,,θ)be a Higgs bundle over M with an initial Hermitian metric H0.If the initial data satisfiesfor some positive constant C0,then the following Hermitian-Einstein flow has a solution which is de fined on M ×[0,∞). In this section we will prove the existence of Hermitian-Einstein metric on complete noncompact Hermitian manifold.We will proceed by the direct elliptic method.The argument is similar to that in[33]for holomorphic vector bundle case.The following are the main assumptions we will need. De finition 5.1(Positive spectrum) Let M be a complete Hermitian manifold.We say the holomorphic Laplace operatorhas positive first eigenvalue,if there exists a positive number c such that for any compactly supported smooth function φ one has De finition 5.2(L2-Sobolev inequality) Let M be a complete Hermitian manifold of complex dimension m.We say the holomorphic Laplace operatorsatis fies L2-Sobolev inequality,if there exists a positive constant SMsuch that for any compact supported smooth function φ one has In order to use the direct elliptic method,we now introduce a new distance function instead of σ.For two metrics H and K,we de fine The relationship between σ and τ is given by Now choose a compact exhaustion sequenceas in Section 4.By our previous discussion in Section 3,we know that over each Ωithere exists a Hermitian metric Hisuch that where H0is the given initial metric on E.Denote hi=Hiand τi= τ(H0,Hi).Then by Corollary 2.7 we can see that Next we impose the following condition on the holomorphic Laplace operator. Condition 5.3There exists a positive number p>0 such that for every non-negative function f∈Lp(M),there exists a non-negative solution u∈C0(M)of Theorem 5.4Let(M,g)be a complete Hermitian manifold,and(E,,θ)be a Higgs bundle over M with an initial Hermitian metric H0.Assume for the holomorphic Laplace operator∆,Condition 5.3 is satis fied with some positive number p.Assume further thatThen there exists a Hermitian-Einstein metric H on E. ProofLet u be a solution to.If M satis fies Condition 5.3,this together with(5.1)and the maximun principle shows that holds for any x∈Ωi.Using this C0-estimate,and proceeding as how we did in Section 4 shows that Hiconverges uniformly over any compact subset of M to a smooth Hermitian metric H satisfying over any compact subset.Hence H is a Hermitian-Einstein metric over the whole manifold M. Therefore we complete the proof of Theorem 1.1 by the following lemma. Lemma 5.5(see[33,Lemma 6.4,Lemma 6.5])Let M be a complete Hermitian manifold of complex dimension m. 1)Assume the holomorphic Laplace operator˜∆has positive first eigenvalue(M).Then for a non-negative function f∈Lp(M),where p≥2,the following equation has a non-negative solution 2)Assume˜∆satis fies the L2-Sobolev inequality.Then for a non-negative function f∈Lp(M),where 2≤p
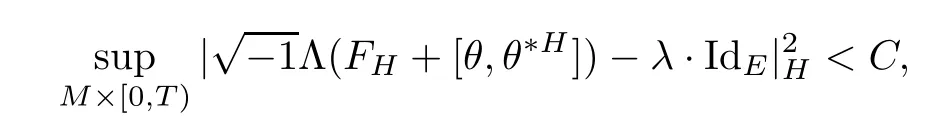
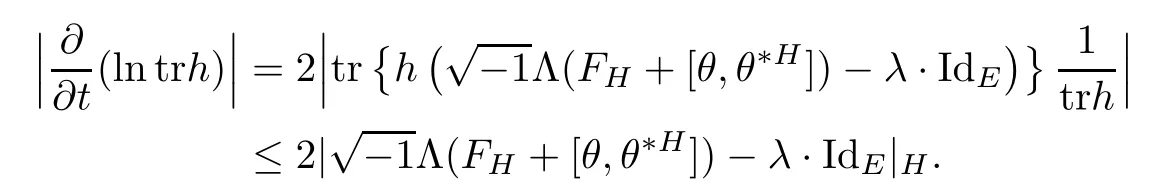
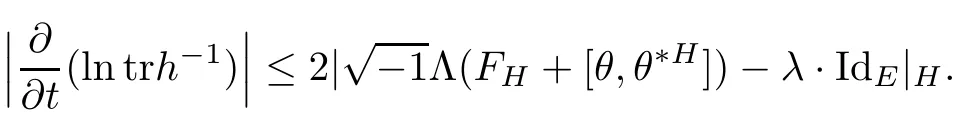

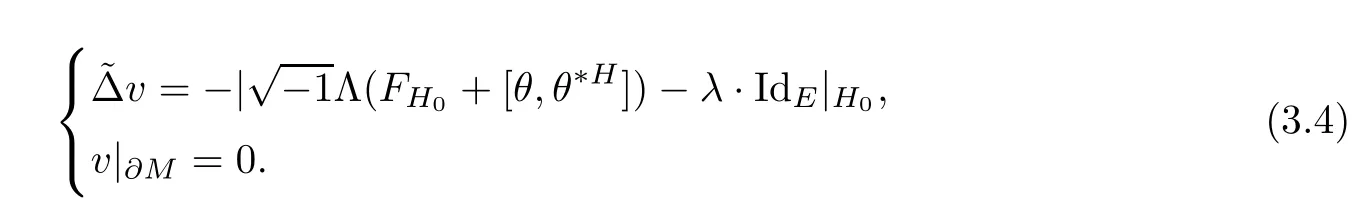
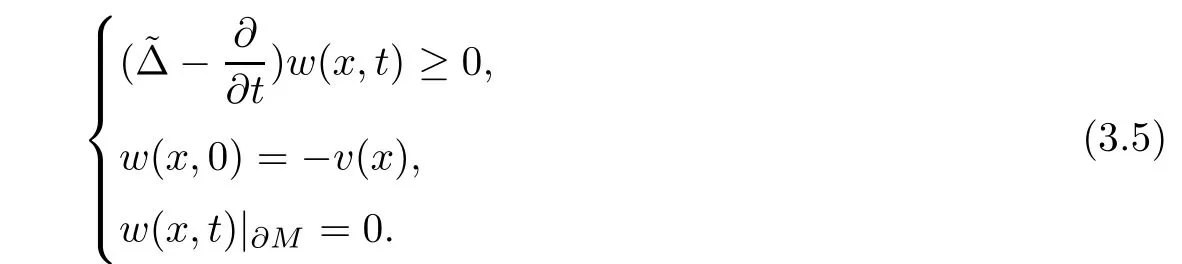

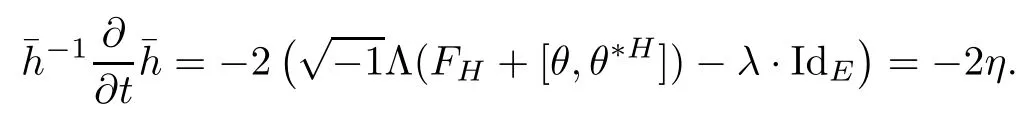
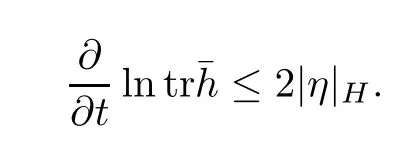

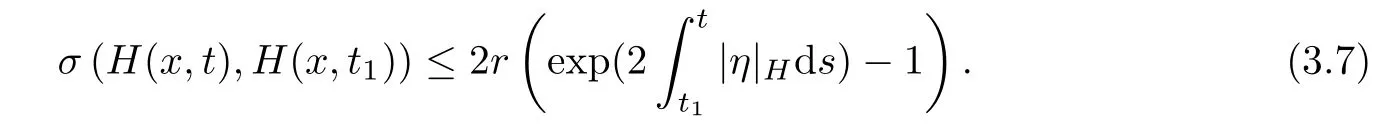
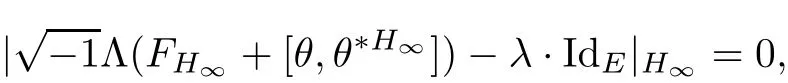

4 Hermitian-Einstein Flow Over Complete Hermitian Manifolds

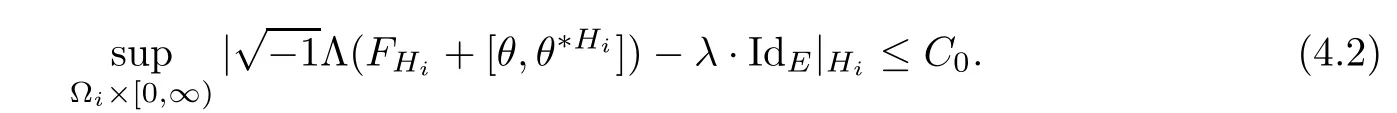
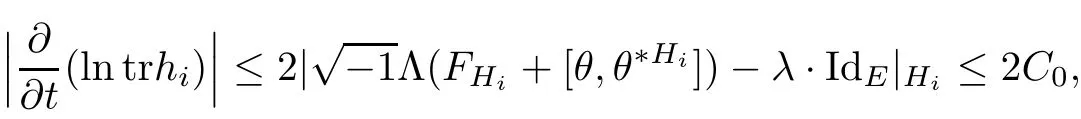
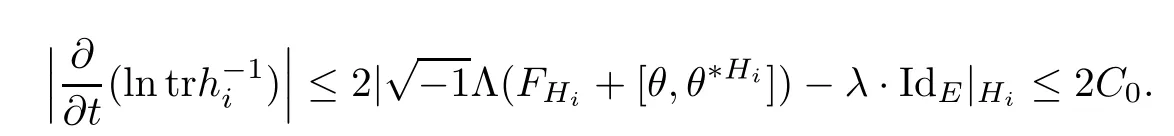
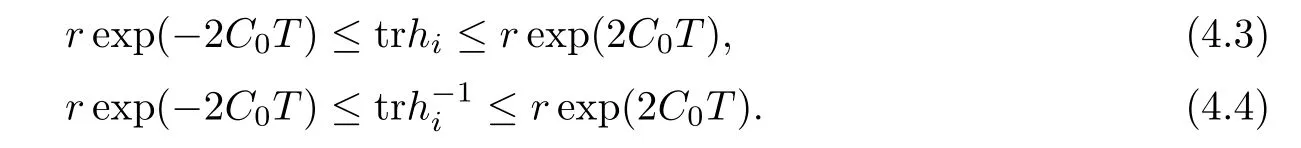

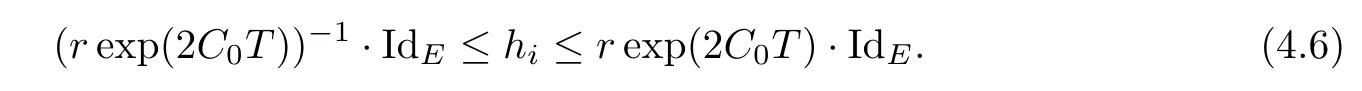
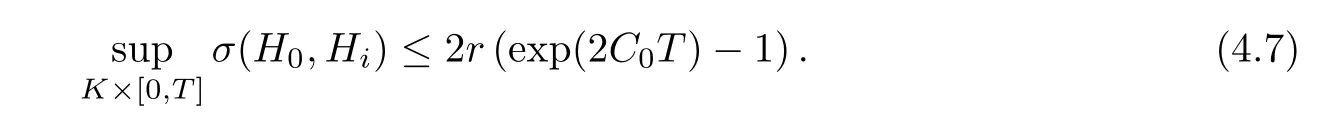
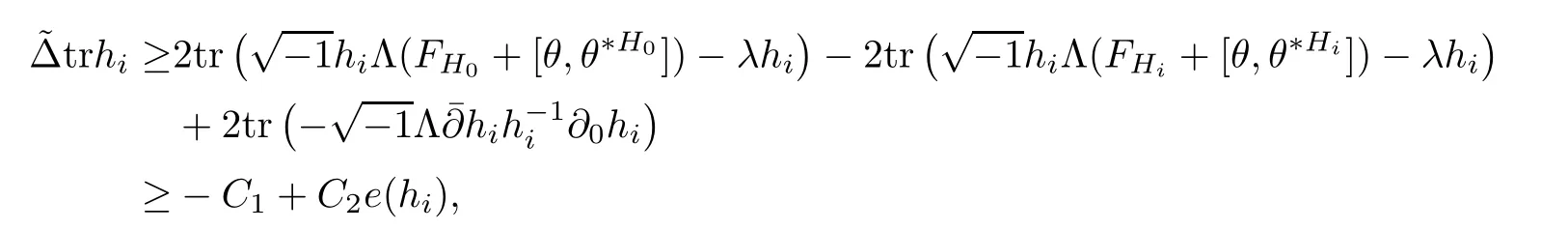
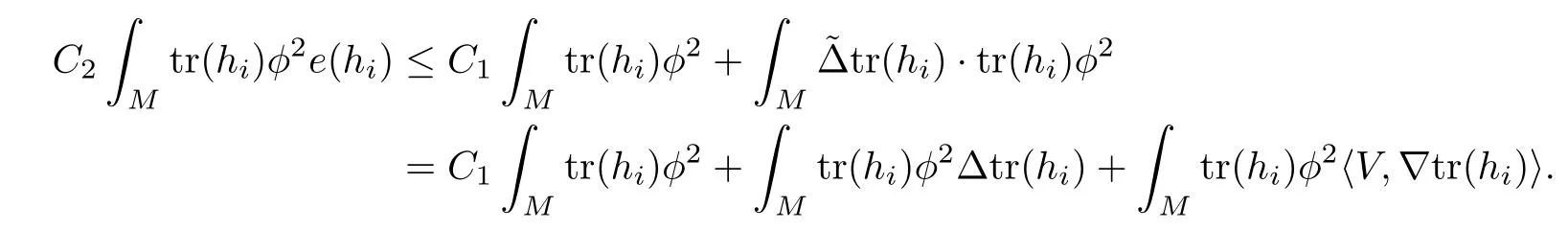

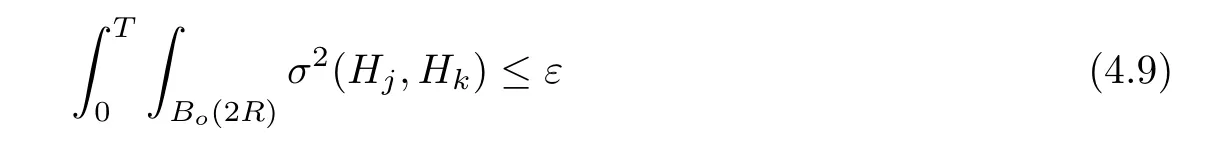

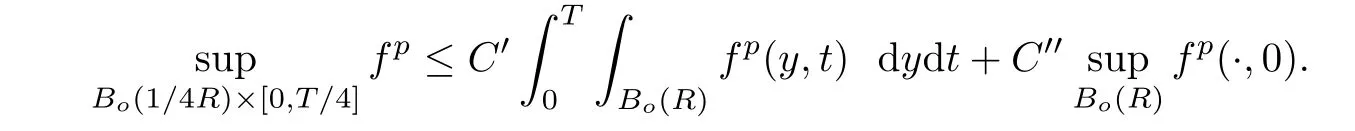
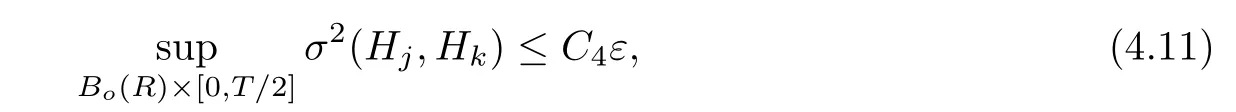

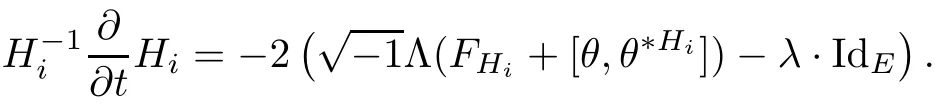
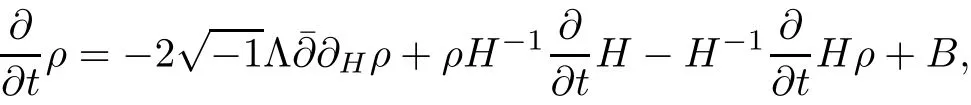
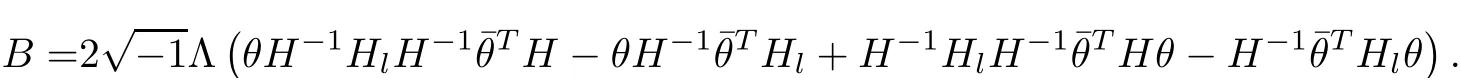
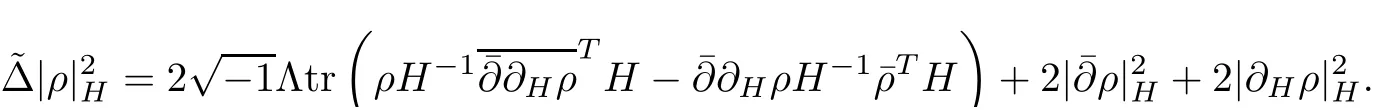
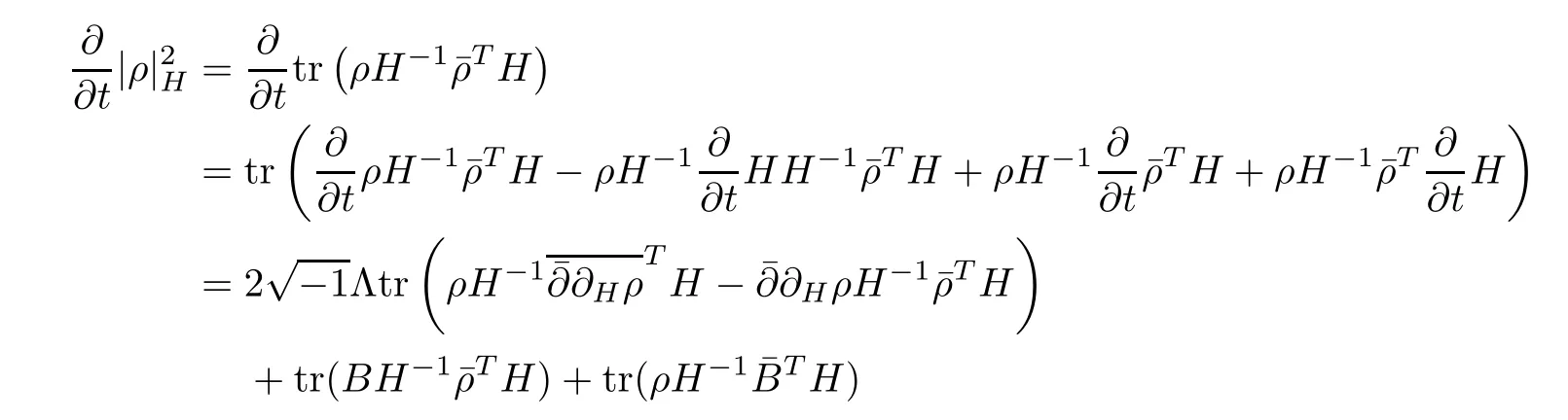

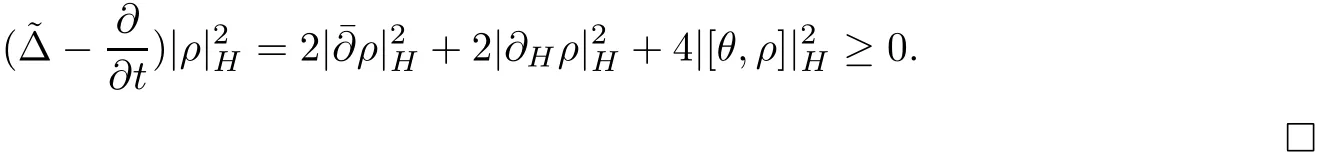
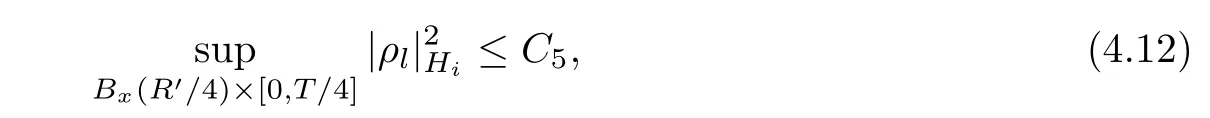

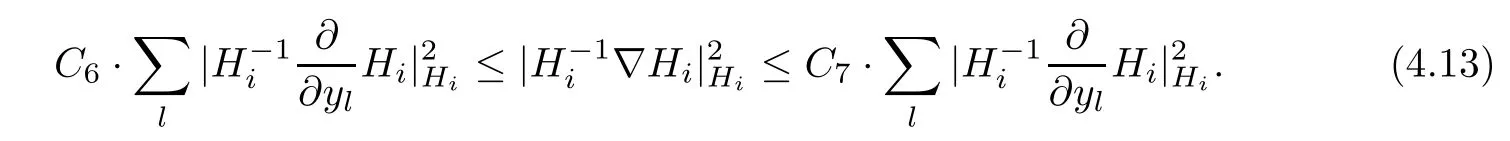
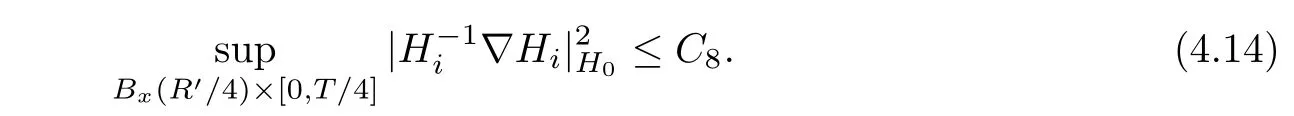
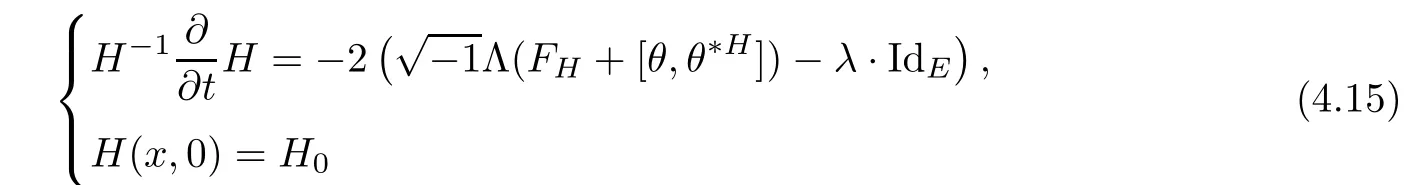
5 Hermitian-Einstein Metrics on Complete Hermitian Manifolds
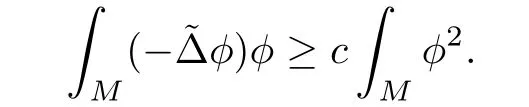
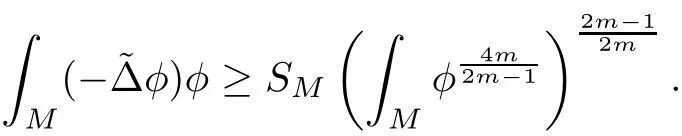
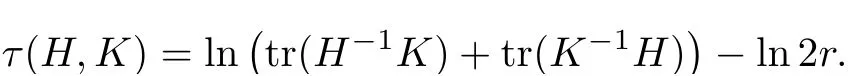

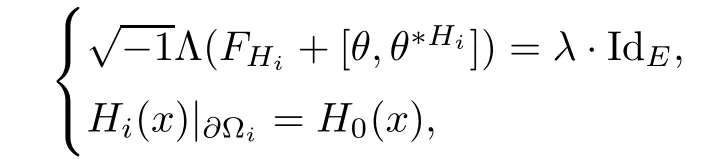
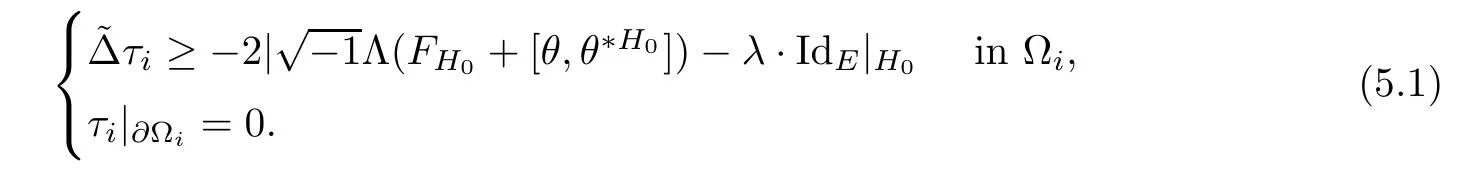
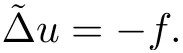
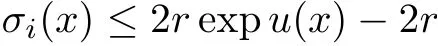
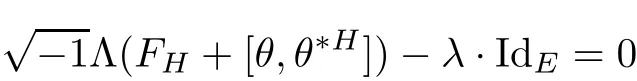

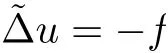
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- BOUNDEDNESS OF MULTILINEAR LITTLEWOOD-PALEY OPERATORS ON AMALGAM-CAMPANATO SPACES∗
- GLOBAL SIMPLE WAVE SOLUTIONS TO A KIND OF TWO DIMENSIONAL HYPERBOLIC SYSTEM OF CONSERVATION LAWS∗
- COMPLEX INTERPOLATION OF NONCOMMUTATIVE HARDY SPACES ASSOCIATED WITH SEMIFINITE VON NEUMANN ALGEBRAS∗
- THE ENERGY CONSERVATIONS AND LOWER BOUNDS FOR POSSIBLE SINGULAR SOLUTIONS TO THE 3D INCOMPRESSIBLE MHD EQUATIONS∗
- EXISTENCE OF SOLUTIONS OF nTH-ORDER NONLINEAR DIFFERENCE EQUATIONS WITH GENERAL BOUNDARY CONDITIONS∗
- LOCAL CONVERGENCE OF INEXACT NEWTON-LIKE METHOD UNDER WEAK LIPSCHITZ CONDITIONS∗
