EXISTENCE OF SOLUTIONS OF nTH-ORDER NONLINEAR DIFFERENCE EQUATIONS WITH GENERAL BOUNDARY CONDITIONS∗
2020-04-27AlbertoCABADA
Alberto CABADA
Departamento de Estat´ıstica,An´alise Matem´atica e Optimizaci´on,Instituto de Matem´aticas,Facultade de Matem´aticas,Universidade de Santiago de Compostela,Santiago de Compostela,Galicia,Spain
E-mail:alberto.cabada@usc.es
Nikolay DIMITROV
Depatment of Mathematics,University of Ruse,Ruse 7000,Bulgaria
E-mail:ndimitrov@uni-ruse.bg
Abstract The aim of this paper is to prove the existence of one or multiple solutions of nonlinear difference equations coupled to a general set of boundary conditions.Before to do this,we construct a discrete operator whose fixed points coincide with the solutions of the problem we are looking for.Moreover,we introduce a strong positiveness condition on the related Green’s function that allows us to construct suitable cones where to apply adequate fixed point theorems.Once we have the general existence result,we deduce,as a particular case,the existence of solutions of a second order difference equation with nonlocal perturbed Dirichlet conditions.
Key words difference equation;multiplicity of solutions;Green’s function;positive solutions;parameter dependence
1 Introduction
It is very well known that the theory of difference equations appears in many different fields as,among others,computer science,economical models or population dinamics.We refer to the reader the classical books by Agarwal[1]and Kelly and Peterson[15]for a general overview on the basic theory of this type of equations,coupled with some interesting examples and mathematical models of the related topics.
More recently,several authors focused their investigation in proving the existence and multiplicity of solutions of difference problems by using various methods from nonlinear analysis.
In particular,the method of upper and lower solutions coupled to Leray-Schauder degree theory and some different kinds of fixed point theorems in cones are very useful tools to obtain the existence of solutions of nonlinear boundary value problems.We make special mention of the paper[16],where Legget and Williams established a fixed point result,which was extended during the next decades.Such results were improved by the same authors in[17],where,as an application,it was proved the existence of multiple solutions of the following third order boundary value problem

with 0< ξ1< ξ2< ···< ξm−2<1,ki∈ R+for i=1,···,m − 2 and
A result in the line of Legget-Williams fixed point theorem,that ensures the existence of at least a positive fixed point on different sets de fined by means of suitable functionals,was obtained in[2].
In[8]the authors generalized the triple fixed point theorem of Legget-Williams,which allow them to prove the existence of three positive symmetric solutions of the discrete second order nonlinear conjugate boundary value problem
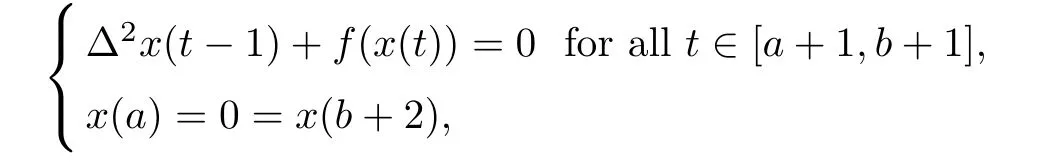
where f:R→R is continuous and nonnegative for x≥0.
Recently,in[5],the authors proved a new fixed point theorem that gives us a different existence result for problem studied in[2].
In[14]it was proved the existence of one or multiple solutions of a wide range of nonlinear ordinary differential equations,coupled to boundary value conditions,by imposing the following hypothesis on the kernel G:
(Pg1)there exist Φ,k1and k2continuous functions on[a,b]such that Φ(s)>0 for all s∈ (a,b),0 This kind of conditions were introduced in[9]and ensured the validity of monotone iterative techniques in a general framework.Moreover,under this condition,a characterization of the set of real parameters where the Green’s function has constant sign is given.The extremes of the corresponding intervals are the first eigenvalues of the operator de fined on related functional spaces,see[11–13]for details. In this paper,we assume the discrete version of the above hypothesis and,moreover (F)f:I×[0,∞)→ [0,∞)is a continuous function. Here we denote I ≡ {a,···,b}with b−a ≥ 2. We obtain multiplicity results for a family of n-th order boundary value problems given by here Li:Rb−a+1→ R, i=1,···,n are linear operators,for which the following condition for the related Green’s function is ful fi lled. (G) There exist non-negative functions on I, Φ,l1and l2,such that Φ(s)>0 for all s∈ J ≡ {a+1,···,b−1},0 As an application of these results,in Section 4 we continue the ones given in[10]for a second order problem.Moreover,we prove the existence of at least two or three solutions of the considered problem. It is well known that,provided problem(1.1)–(1.2)has u ≡ 0 as its unique solution when f ≡ 0,the solutions of problem(1.1)–(1.2)are given as the fixed points of the difference operator where G(k,s)is its associated Green’s function. Thus,in order to find the fixed points of operator T,we previously study in Section 3,the existence of at least two or three fixed points of the difference operator. In this section,in order to study the existence of some fixed points of the difference operator,de fined in(1.4)in an appropriate cone,we give some basic de finitions and we recall some previous results. First of all,we recall some de finitions. De finition 2.1Let B be a real Banach space.A nonempty closed convex set P⊂B is called a cone if it satis fies the following two conditions. 1) λx∈P for all x∈P and λ≥0. 2)If x∈P and−x∈P,then x=0. Then,consider a subinterval I1={a1,···,b1} ⊂ I such that l1(k)>0 for all k ∈ I1and denote Finally,let us consider the cone Now,we give de finitions of concave and convex functional on a cone. De finition 2.2A map α is said to be a nonnegative continuous concave functional on a cone P of a real Banach space B if α:P →[0,+∞)is continuous and Similarly,a map β is said to be a nonnegative continuous convex functional on a cone P of a real Banach space B if β:P →[0,+∞)is continuous and Let β,γ and θ,be nonnegative continuous convex functionals on the cone P,and α and ψ,nonnegative concave functionals on P.Thus,for nonnegative real numbers d,p and q,we de fine the following subspaces of the cone P: Recall a result,proved in[6],which ensures the existence of two fixed points on the cone P. Theorem 2.3Let P be a cone in a real Banach space B.Let α and γ be increasing and nonnegative continuous functionals on P.Let θ be a nonnegative continuous functional on P with θ(0)=0 such that for some positive constants r and M, Assume that there exist two positive numbers p and q with p i) α(Lu)>r for all u ∈ ∂P(α,r), ii) θ(Lu) iii)P(γ,p)6= ∅ and γ(Lu)>p for all u ∈ ∂P(γ,p). Then,L has at least two fixed points u1and u2such that and Finally,we introduce a result,see[4],that ensures the existence of three fixed points of L on the cone P. Theorem 2.4Let P be a cone in a real Banach space B,and let r and M be positive numbers.Assume that α and ψ are nonnegative,continuous and concave functionals on P,and γ,β and θ are nonnegative,continuous and convex functional on P with a){u ∈ P(γ,θ,α,p,q,r)|α(u)>p}6∅ and α(Lu)>p for u ∈ P(γ,θ,α,p,q,r), b){u ∈ P(γ,β,ψ,h,d,r)|β(u) c) α(Lu)>p for all u ∈ P(γ,α,p,r)with θ(Lu)>q, d) β(Lu) Then,L has at least three fixed points u1,u2and u3such that This section is devoted to prove the existence of multiple solutions of problem(1.1)–(1.2).To this end,we previously obtain some useful properties of operator T de fined in(1.4). Let u∈P be arbitrarily chosen.Clearly,from condition(G),we have that Tu≥0 on I and,moreover,we deduce that the following inequalities are ful fi lled for all k∈I, In other words,T:P→P. Moreover,due to the continuity of function f,it is clear that T is a completely continuous operator. Now,from Theorems 2.3 and 2.4,we deduce the existence of two or three fixed points,respectively,of operator T de fined in(1.4).We follow the steps given in[3,14]. Theorem 3.1Suppose that there exist positive integers p,q and r such that p Then if G(k,s)satis fies condition(G),then operator Thas at least two fixed points,u1and u2,such that ProofLet us denote and For all u ∈ P we have that α(u)≤ θ(u)≤ γ(u).The fact that u ∈ P gives us that Hence,for all λ ≥ 0 and u ∈P,we verify that Using(i)and(G),we deduce the following inequalities The fact that α(u)=r gives us that there exists k1∈ I1with u(k1)=r.According to(i)we have.Since Φ >0 on I1,the inequality for α is strict too,and it follows that Following the previous arguments,θ(u)=q gives us that there exists k2∈ I1with u(k2)=q.Using(ii)and the fact that Φ>0 on J we arrive at Finally,using(iii)and(G),one can check that Thus γ(Tu)>p for all u ∈ ∂P(γ,p)and all the assumptions of Theorem 2.3 are veri fied. Hence,Thas at least two fixed points on P,u1and u2,such thatandMoreover,and Remark 3.2We point out that due to the properties that the fixed points u1and u2satisfy,both of them are not trivial. As an application of Theorem 2.4,we formulate the next result that gives us the existence of at least three fixed points of operator T. Theorem 3.3Let p,q and r be positive integers such that Suppose that the function fsatis fies the assumptions below Then,operator Thas at least three fixed points u1,u2,u3such thatand ProofLet α,θ,γ are de fined as in(3.1)–(3.3),Ψ(u)= α(u)and β(u)= θ(u).It is easy to check α and Ψ are concave and nonnegative functionals in P,while β,θ and γ are convex and nonnegative functionals in P. We already proved that T(P)⊂P.Now,let us show thatIndeed,if,then using(a)it follows that One can check that uq(k)=q belongs to the set Thus If there exists s1∈ I1such that u(s1)>q,then from the last inequality,we have α(Tu)>q.Otherwise,if u(s)=q for all s∈I1,then by using(c),we obtain Similarly as above,function up(k)=p belongs to the set so Suppose that u ∈ P(γ,α,q,r)and θ(Tu)>q.One can verify that Thus,all the assumptions of Theorem 2.4 are veri fied,which ensures us the existence of at least three critical points such thatandwith Remark 3.4We point out that the fixed points u1and u2obtained in previous result are not trivial.However,without additional assumptions on the data of operator T,we cannot ensure such property for u3. In this section,in order to maintain a similar notation to the one used in[10],we rede fine I={0,···,N}and I1=J={1,···,N − 1},i.e.,a=0,b=N,a1=1 and b1=N − 1. Our goal in this section is to extend the results given in[10]concerning the following second order problem with perturbed Dirichlet conditions In that case,existence of one or two nontrivial solutions are deduced by means of the Krasnoselski˘ı’s fixed point theorem.In this section,as a direct application of the previous fixed point theorems,we deduce the existence of two or three solutions of problem(4.1)–(4.2).To this end,we assume the following property So,by denoting J1={1,···,N},we have the following result Theorem 4.1(see[10,Theorem 2.1]) Ifµsatis fies hypothesis(H1)then there is G the Green’s function related to the linear part of problem(4.1)–(4.2).Moreover G(k,s)>0 for all k∈J1and s∈J,and there are two positive constants 0 for all k∈J1and s∈J. Since G(0,s)=0 for all s∈J,it is clear that condition(G)is ful fi lled in this situation. Remark 4.2On[10]some explicit estimations of the constants m1and M1are obtained.Such expressions are very complicated and depends on the relative positions of s and a and b. In particular,we have that Φ(s)=G(N,s),l1(0)=l2(0)=0,and As consequence,the constants de fined in(2.1)satisfy,in this case Using these properties,we deduce,as in Theorems 3.1 and 3.3,the existence of two or three solutions(with at least two of them non trivial on J)respectively,of problem(4.1)–(4.2). Theorem 4.3Suppose that there exist positive integers p,q and r such that p Then problem(4.1)–(4.2)has at least two nontrivial solutions,u1and u2,such that Theorem 4.4Let p,q and r be positive numbers such that Assume,moreover,that the function fsatis fies the following conditions Then problem(4.1)–(4.2)has at least three solutionssuch thatu1(k) In the sequel,we consider a particular case of problem(4.1)–(4.2).We fi x the values of c=1,d=N−1 andµ=.It is easy to check that condition(H1)holds.In this case the Green’s function is given by the expression Moreover,from(4.3)we have that Using similar arguments we deduce that M1=2. By direct calculations we obtain that Finally,as a direct consequence of Theorems 4.3 and 4.4,we obtain the following results. Theorem 4.5Suppose that there exist positive integers p,q and r such that p Then problem(4.1)–(4.2)with c=1,d=N − 1 andhas at least two nontrivial solutions,u1and u2such that Theorem 4.6Let p,q and r be positive numbers such that Assume,moreover,that the function fsatis fies the following conditions(c)f(k,u)≥for all k∈J and u∈[q,Nq],being the inequality strict for u=q. Then problem(4.1)–(4.2)with c=1,d=N − 1 and µ =has at least three solutionssuch thatandwith
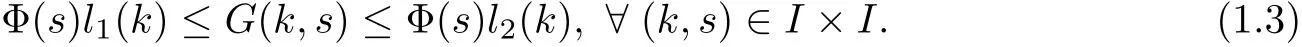

2 Description of the Problem and Some Previous Fixed Point Existence Results
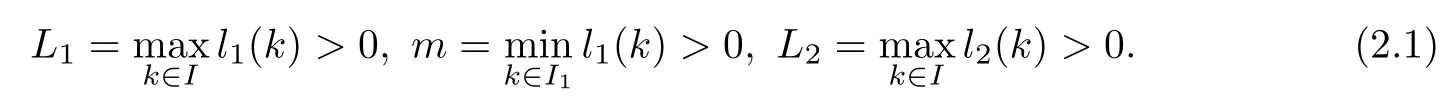


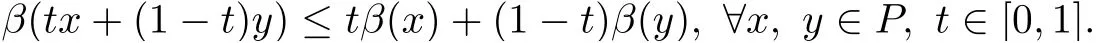
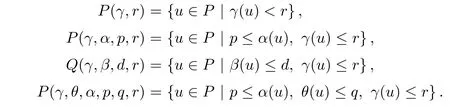
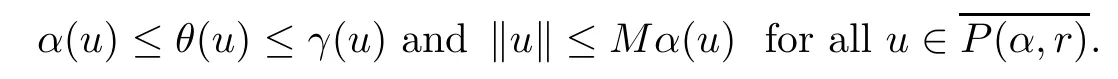
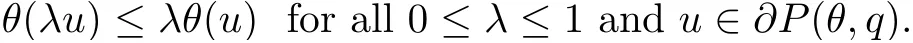
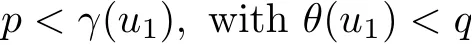
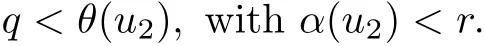
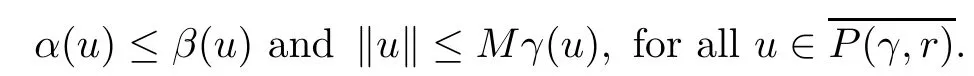

3 Existence of Multiple Fixed Points
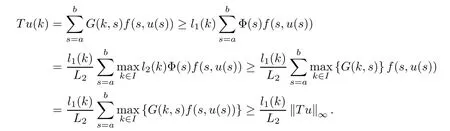
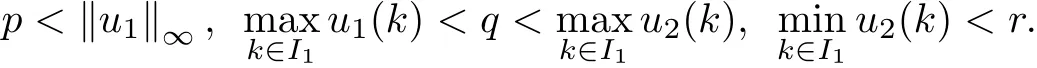


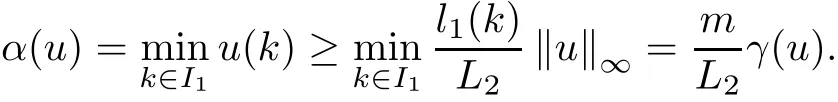

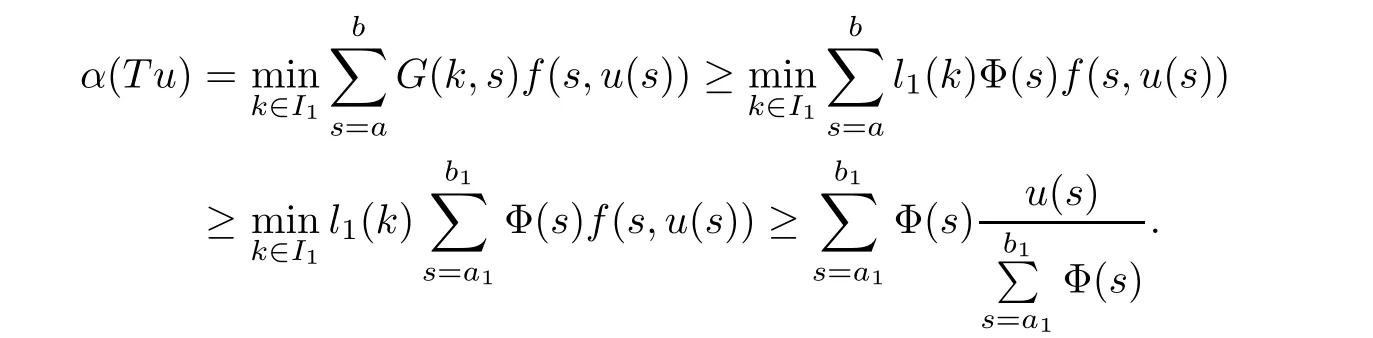
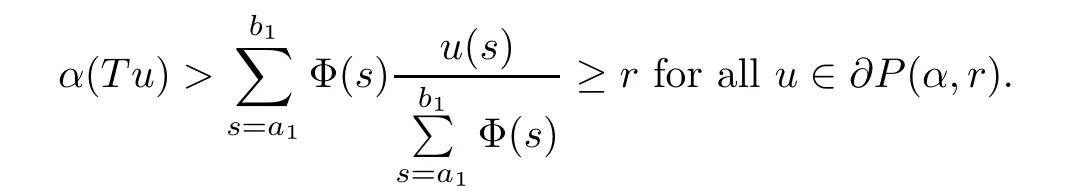
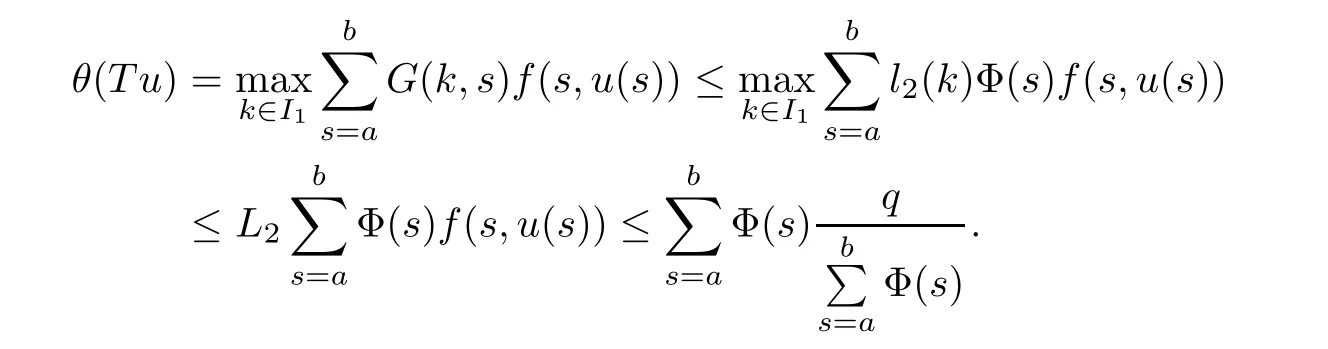
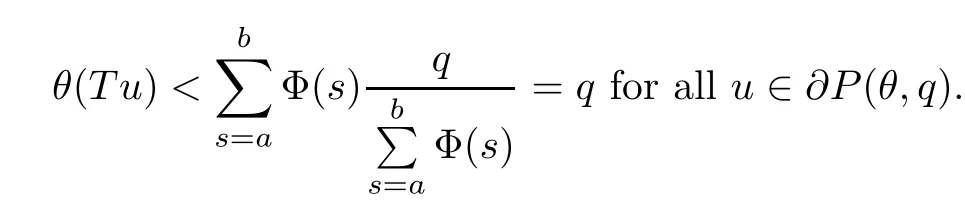
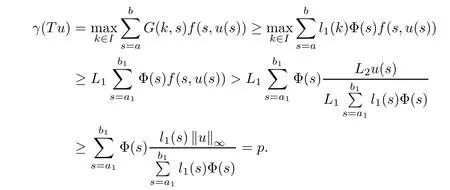
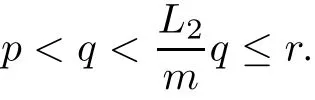
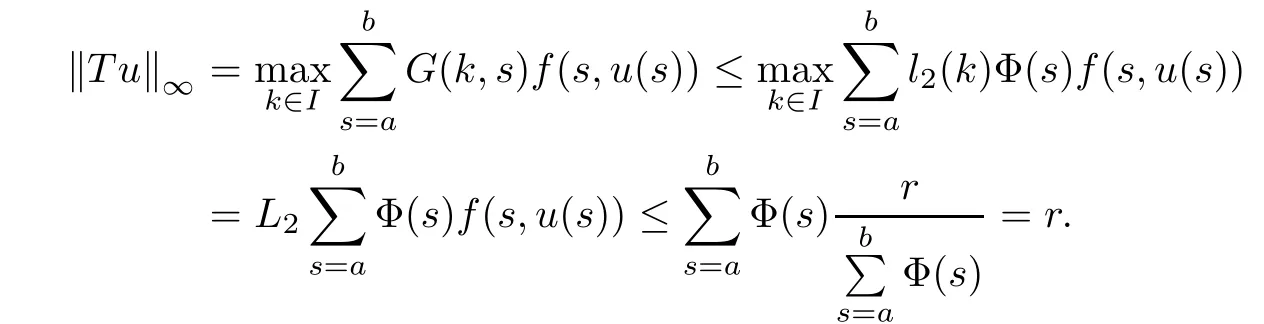

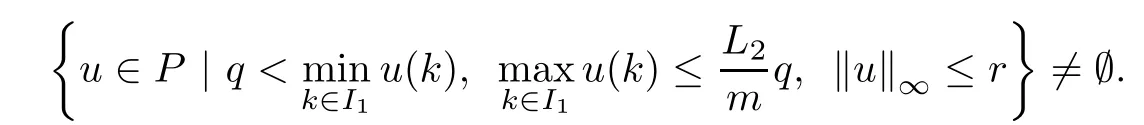
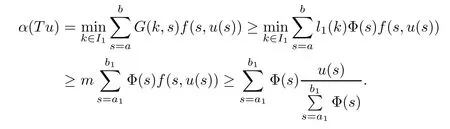
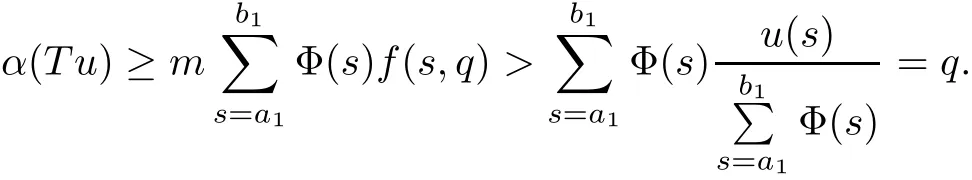

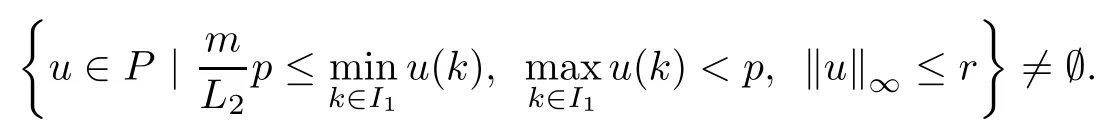
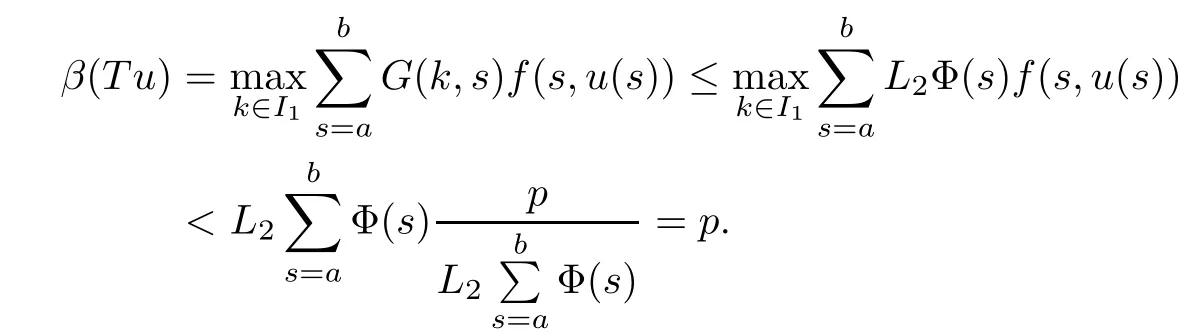
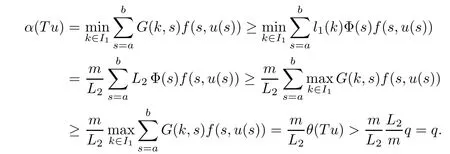
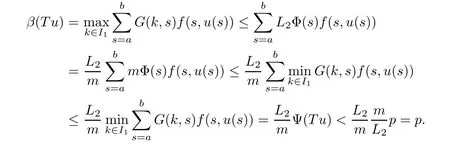
4 An Application to a Second Order Problem
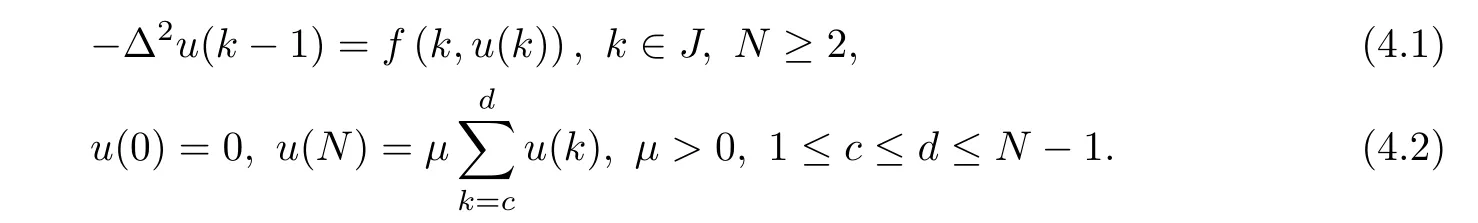

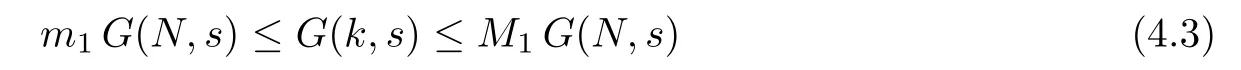
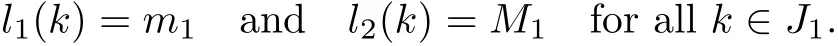
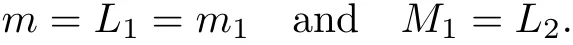
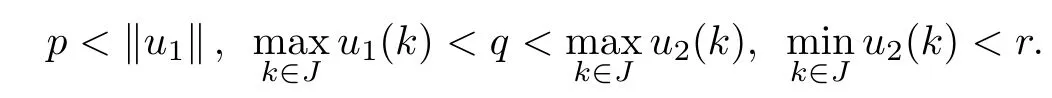

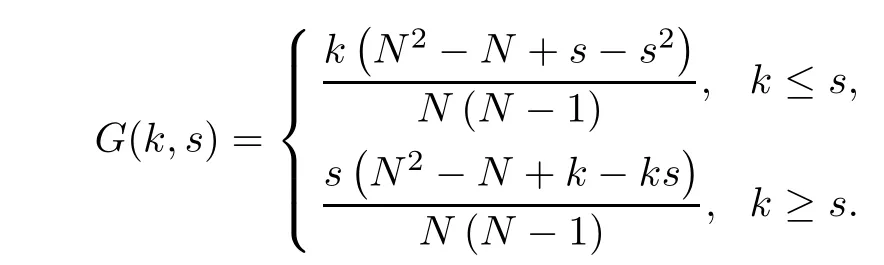
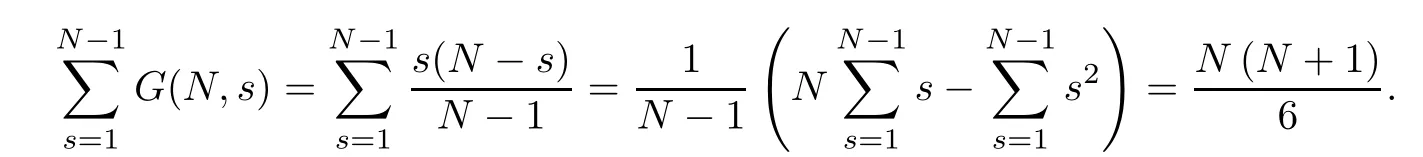

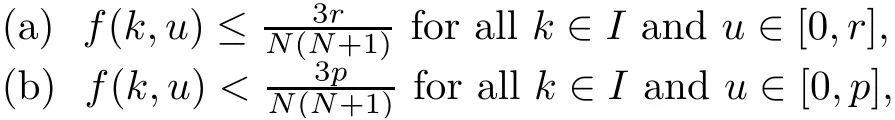
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- BOUNDEDNESS OF MULTILINEAR LITTLEWOOD-PALEY OPERATORS ON AMALGAM-CAMPANATO SPACES∗
- GLOBAL SIMPLE WAVE SOLUTIONS TO A KIND OF TWO DIMENSIONAL HYPERBOLIC SYSTEM OF CONSERVATION LAWS∗
- COMPLEX INTERPOLATION OF NONCOMMUTATIVE HARDY SPACES ASSOCIATED WITH SEMIFINITE VON NEUMANN ALGEBRAS∗
- THE ENERGY CONSERVATIONS AND LOWER BOUNDS FOR POSSIBLE SINGULAR SOLUTIONS TO THE 3D INCOMPRESSIBLE MHD EQUATIONS∗
- HERMITIAN-EINSTEIN METRICS FOR HIGGS BUNDLES OVER COMPLETE HERMITIAN MANIFOLDS∗
- LOCAL CONVERGENCE OF INEXACT NEWTON-LIKE METHOD UNDER WEAK LIPSCHITZ CONDITIONS∗
