COMPLEX INTERPOLATION OF NONCOMMUTATIVE HARDY SPACES ASSOCIATED WITH SEMIFINITE VON NEUMANN ALGEBRAS∗
2020-04-27TurdebekBEKJAN吐尔德别克
Turdebek N.BEKJAN(吐尔德·别克)
College of Mathematics and Systems Science,Xinjiang University,Urumqi 830046,China
E-mail:bekjant@yahoo.com
Kordan N.OSPANOV
Faculty of Mechanics and Mathematics,L.N.Gumilyov Eurasian National University,Astana 010008,Kazakhstan
E-mail:ospanov−kn@enu.kz
Abstract We proved a complex interpolation theorem of noncommutative Hardy spaces associated with semi- finite von Neumann algebras and extend the Riesz type factorization to the semi- finite case.
Key words subdiagonal algebra;complex interpolation;noncommutative Hardy space;semi- finite von Neumann algebra
1 Introduction
This paper deals with the complex interpolation and Riesz type factorization of noncommutative Hardy spaces associated with semi finite von Neumann algebras.Let M be a semi finite(respectively, finite)von Neumann algebra equipped with a normal faithful semi finite(respectively, finite)trace τ.Given 0
Let D be a von Neumann subalgebra of M such that the restriction of τ to D is still semi finite.Let E be the(unique)normal positive faithful conditional expectation of M with respect to D such that τ◦ E= τ.A subdiagonal algebra of M with respect to E(or D)is a w∗-closed subalgebra A of M satisfying the following conditions
(i)A+J(A)is w∗-dense in M,
(ii)E(xy)=E(x)E(y),∀x,y∈A,
(iii)A∩J(A)=D.
The algebra D is called the diagonal of A.
It was proved by Ji[19](respectively,Exel[16])that a subdiagonal algebra A of a semi finite(respectively, finite)von Neumann algebra M is automatically maximal,i.e.,A is not properly contained in any other subalgebra of M which is a subdiagonal algebra with respect to E.This maximality yields the following useful characterization of A:

where A0=A∩kerE(see[1]).
For p<∞we de fine Hp(A)to be the closure of A∩Lp(M)in Lp(M),and for p=∞we simply set H∞(A)=A for convenience.These are the so-called Hardy spaces associated with A.They are noncommutative extensions of the classical Hardy spaces on the torus T.For the finite case,most results on the classical Hardy spaces on the torus were established in this noncommutative setting.We refer to[1,8–11,25,28,32].Here we mention only the interpolation theorem and the Riesz factorization theorem directly related with the objective of this paper.
In[27],Pisier gave a new proof of the interpolation theorem of Peter Jones(see[20]or[7],p.414).He obtained the complex case of Peter Jones’theorem as a consequence of the real case.The Pisier’s method does extend to the noncommutative case and the case of Banach space valued Hp-spaces(see§2 in[27]).Pisier and Xu[28]obtained the following noncommutative version of Peter Jones’theorem.
Theorem 1.1(Pisier/Xu) Let M be a finite von Neumann algebra,and let A be a subdiagonal algebra of M.If 0 and where C depends only on p0,p1and θ. The first-named author[2],using Pisier’s method,proved that the real case of Peter Jones’theorem for noncommutative Hardy spaces associated with semi finite von Neumann algebras holds(also see[33]).The main purpose of the present paper is to prove the complex case of Peter Jones’theorem for noncommutative Hardy spaces associated with semi finite von Neumann algebras,i.e.,to extend the above Pisier/Xu’s theorem to the semi finite case. The Riesz factorization asserts that Hp(A)=Hq(A)·Hr(A)for any 0 This result was proved in[31]for p=q=2,in[25]for r=1,and independently in[23]and in[28]for 1≤p,q,r≤∞,and in[3]for the general case as above.We prove a similar result in the semi finite case. The organization of the paper is as follows.In Section 2,we prove the complex interpolation theorem.Section 3 is devoted to the Riesz type factorization theorem.In Section 4,we give some applications of the complex interpolation theorem. We will keep all previous notations throughout the paper.Unless explicitly stated otherwise,M always denotes a semi finite von Neumann algebra equipped with a semi finite faithful trace τ,and A a subdiagonal algebra of M. Then F0(X0,X1)becomes a quasi-Banach space.Let 0<θ<1.The complex interpolation norm on X0∩ X1is de fined for θ by We denote by(X0,X1)θthe completion of It is well-known that if(X0,X1)is a compatible couple of complex Banach spaces,then the de finition of the interpolation spaces here coincides with that of[12]. Let e be a projection in D.We set and let Eebe the restriction of E to Me.Using Lemma 3.1 in[2]we obtain that Aeis a subdiagonal algebra of Mewith respect to Ee(or De). Since D is semi finite,we can choose an increasing family of{ei}i∈Iof τ- finite(τ(ei)< ∞)projections in D such that ei→1 strongly,where 1 is identity of M(see Theorem 2.5.6 in[30]).Throughout,{ei}i∈Iwill be used to indicate this net. Lemma 2.1Let 0 ProofIt is clear that Hp(A)⊆(Hp0(A)+Hp1(A))∩Lp(M)(see Theorem 6.3 in[2]).Conversely,if x∈(Hp0(A)+Hp1(A))∩Lp(M),then By Lemma 3.1 in[2],we have that Hence Since Aeiis a subdiagonal algebra of the finite von Neumann algbra Mei,by Proposition 3.3[3],we get Note that since ei→1 strongly,we getand(see Lemma 2.3 in[21]).Therefore Thus x∈Hp(A).This gives the desired result. Theorem 2.2Let 0 and where C depends only on p0,p1and θ. ProofBy Theorem 4.1 in[36],we have(Lp0(M),Lp1(M))θ=Lp(M)with equal norms.Hence On the other hand, Using(2.1)we obtain that(Hp0(A),Hp1(A))θ⊂ Hp(A)and Recall that Aeiis a subdiagonal algebra of the finite von Neumann algbra Mei(i∈I).By Theorem 1.1,we have that Hence and Let a∈Hp(A).Similar to(2.2),we deduce that Using(2.4)we obtain that since{ei}i∈Iis increasing and I is a directed set.Thus{eiaei}i∈Iis a Cauchy net in(Hp0(A),Hp1(A))θ.Therefore,there exists y in(Hp0(A),Hp1(A))θsuch that where the in fi mum runs over all possible factorizations of x as above. It is clear that Hp(A)⊙Hq(A)⊂Hr(A)and Proposition 3.1Let 0 ProofSuppose that r≥ 1.If x,y∈ Hp(A)⊙Hq(A),then for ε>0,there exist sequences(an)n≥1,(cn)n≥1in Hp(A)and sequences(bn)n≥1,(dn)n≥1in Hq(A)such that and On the other hand,(3.1)insures that>0 for any non-zero x ∈ Hp(A)⊙Hq(A).Thusis a norm on Hp(A)⊙Hq(A). Let us prove the completeness of the norm.Let(xk)k≥1be a sequence in Hp(A)⊙Hq(A)such thatBy(3.1),It follows thatSetLet ε>0 be given and select a sequencein Hp(A)and a sequencein Hq(A)such thatand for every k.Since The case 0 Theorem 3.2Let 0 ProofWe prove only the case r≥1.The proof of the case r<1 is similar.By Lemma 3.1 in[2],we know that eiHr(A)ei=Hr(Aei)(i∈I).Since Aeiis a subdiagonal algebra of the finite von Neumann algebra Mei,by Theorem 3.4 in[3],for xi∈ Hr(Aei)and ε>0 there exist yε∈ Hp(Aei)and zε∈ Hq(Aei)such that Hence xi∈Hp(A)⊙Hq(A)and so eiHr(A)ei⊂Hp(A)⊙Hq(A)(i∈I).Using(3.1)we obtain that Let x∈Hr(A).Similar to(2.2),we have that Notice that{ei}i∈Iis increasing,so eixei−ejxej∈ eiHr(A)eifor any i≥ j.Applying(3.3)we obtain that Similar to the proof of Theorem 2.2,we obtain that Hp(A)⊙Hq(A)=Hr(A). By Theorems 2.2 and 3.2,we obtain the following result. Corollary 3.3Let 0 In Section 4 of[24],Marsalli has shown that if x∈Re(A)then there exists a uniquely determined∈Re(A)such that x+∈A and E()=0.The map∼Re(A)→Re(A)is a real linear map and it is called the conjugation map.If 1 For x,y∈M,we de fine Let BMO(M)be the completion of the setwith norm Then under the pairing This identi fication satis fies For more details,see[2]. We use the duality theorem,the reiteration theorem(Theorem 4.5.1,Theorem 4.6.1 in[5])and Wol ff’s theorem(Theorem 2 in[34])to obtain Proposition 4.1Let 0 with equivalent norms. Lemma 4.2Let T:BMO(M)→BMO(M)be de fined by Then T is a bounded linear map with norm at most 2. ProofLet(u,v)∈x+.Thenfor all i∈I.Since eiyei,eivei∈L1(Mei),by Lemma 5.1 and Proposition 5.3 in[25], Since T is a continuous liner extension ofT will be denoted still by Let P:L2(M)→H2(M)be the canonical projection.Then Lemma 4.3Let P′:M → BMO(M)be the map taking x to.Then P′is a continuous linear extension of P,still denoted by P. Proof Thus the proof is completed. We proved the interpolation theorem(Proposition 4.1)with the aid of the boundedness of P on Lp(M)for all 1 For 0 Theorem 4.4Let 0 (ii)If 0 where C is a positive constant. ProofIt is clear that for all 0 (see Lemma 1 and 3 of[26],and Lemma 4.1 in[2]).Since H1(A)is closure of(see Lemma 3.2 in[2]),by(4.2), i.e., Hence Therefore,by(4.3), and so Applying(4.3)and(4.4),we obtain the desired result. (ii)The right inequality is trivial.We choose 0< θ<1 such that 1=.It is clear that,we can view u−i(1−E)(v)as a bounded operator from Hq(A)to Lq(M)for all 0 On the other hand,it is clear that Using Theorem 2.2 and the left inequality in the case 1≤p≤∞,we obtain that From this follows the left inequality.Thus the proof is completed. Appendix:Proof of Theorem 1.1 For easy reference,using the Pisier’s method in[27],we provide a proof of Theorem 1.1(it is stated in[28]without proof,bar a comment that the Pisier’s method may be extended to the noncommutative case.See the remark following Lemma 8.5 there).We denote by L0(M)the linear space of all τ-measurable operators. Let x∈L0(M).We de fine distribution function of x by where e(t,∞)(|x|)is the spectral projection of|x|corresponding to the interval(t,∞).De fine For 0 gives an equivalent norm on Lp,q(M).It is clear that Lp,p(M)=Lp(M)(for details see[14,35]). The space Lp,∞(M)is usually called a weak Lp-space,0 (see Proposition 3.1 in[4]). For 0 In the rest of this appendix(M,τ)always denotes a finite von Neumann algebra equipped with a finite faithful trace τ,and A a subdiagonal algebra of M. Let N be the algebra of in finite diagonal matrices with entries from M and B be the algebra of in finite diagonal matrices with entries from A,i.e., and For x ∈ N with entries xi,de fine Φ(x)to be the diagonal matrix with entries E(xi)and Then(N,ν)is a semi finite von Neumann algebra and B is a semi finite subdiagonal algebra of(N,ν)respect to Φ. Let 0 with equivalent quasi-norms,where 1/p=(1−θ)/p0+θ/p1(for details see[15,28,37]). Using the same method as in the proof of Lemma 4.1 of[27],we obtain that Lemma A.1Let 1 with equivalent norms. ProofLet 1 and On the other hand,(i)and(iii)of Lemma 6.5 in[2],we have that(H1(B),Hr(B))is K-closed with respect to(L1(N),Lr(N))and(Hq(B),B)is K-closed with respect to(Lq(N),N).Hence by Theorem 1.2 in[22],we obtain(H1(B),B)is K-closed with respect to(L1(N),N).Since one can extend Φ to a contractive projection from Lp(N)onto Lp(B∩B∗)for every 1≤ p≤ ∞,we deduce that((B),B0)is K-closed with respect to(L1(N),N).By Holmstedt’s formula(see[5],p.52–53),we get((B),B0)is K-closed with respect to(L1,∞(N),N).Therefore, By Theorem 4.2 in[18],we have that with equivalence of quasi-norms.By(A.1)and Theorem 6.3 in[2],for 1 Applying Theorem 4.2 in[2]and interpolation,we deduce that can be identi fied with Hp,∞(B).Hence,the desired result holds.This completes the proof.? For 1≤p≤ ∞,we de fine Kp:Lp(M)→Lp,∞(N)by Then Indeed,it is clear that for any x∈M, If 1≤p< ∞ and x∈Lp(M),then by Chebychev’s inequality, Using left-Riemann sums,we further get Thus Kpis an isometry.Note that Kpmaps(A)into(B).Let be the mapping canonically associated to Kp.We have following result(see Lemma 4.2 in[27]). Lemma A.2Let 1 into Hp,∞(B),and the norm ofdepends only on p. ProofLet We equip X with the norm Then X becomes a Banach space.It is clear that X ⊂ L1,∞(N)and this inclusion has norm one.Let Then we have that with norm one. For any z∈S,let into From(A.2),it follows that if Re(z)=0,zis a contraction from into X/X0and if Re(z)=1,it is a contraction from M/J(A0)into N/J(B0).Hence,by Stein’s interpolation theorem for analytic families of operators(see Theorem 1 in[13]),we obtain thatis a contraction from into into into Using Lemma A.1,we obtain the desired result.This completes the proof. Lemma A.3Let 1 and the norm of the inclusion depends only on q. ProofLet x∈A.By(A.2)and Lemma A.2,we have that Hence we get(A.4).This completes the proof. Let(X0,X1)be a compatible couple of complex Banach spaces.If X0∩X1is dense in X0and X1,then the dual of X0∩X1can be identi fied with+and the dual of X0+X1can identi fied with,which provides a scheme whereandare compatible.We shall need the second Calder´on interpolation method:let us denote by G(X0,X1)the family of all functions g:→X0+X1satisfying the following conditions •g is continuous on S and analytic in S; • g(k+it1)−g(k+it2)∈Xkfor t1,t2∈R,k=0,1,and The space G(X0,X1)reduced modulo the constant functions and equipped with the norm above,is a Banach space and the second complex interpolation spaces are de fined by which are Banach spaces under the norm Calder´on[12]showed the inclusion(X0,X1)θ⊆ (X0,X1)θand Bergh[6]proved that Proof of Theorem 1.1We first consider the case p0=1,p1=∞.The inclusions(H1(A),A)θ⊂ (L1(M),M)θ=Lp(M)and(H1(A),A)θ⊂ H1(A)imply(H1(A),A)θ⊂Hp(A)(see Proposition 3.3 in[3]),where=1−θ.Conversely,let=1,i.e.,θ=.By Lemma A.3,(L1(M)/J((A)),M/J(A0))1−θ⊂ Hq(A).Using the duality theorem(Theorem 4.5.1 in[5])we obtain that Hence Since A⊂ H1(A),from the de finition,we get that the norm in(H1(A),A)θis the restriction of the norm in((H1(A))∗∗,A)θ.By(A.5),we obtain that Note that A ⊂ Hp(A)and A ⊂ (H1(A),A)θ.Hence,by(A.6)and(A.7),we get Since A is dense Hp(A),using the above inequality and the method in the proof of Theorem 2.2 we obtain that Thus gives the desired result for the case p0=1 and p1=∞. By what is already proved and and the reiteration theorem(see[5],Theorem 4.6.1)we obtain that for any 1≤p0,p1≤∞and 0<θ<1, From this special case,we get the general case. Indeed,since(Hp0(A),Hp1(A))θ⊂(Lp0(M),Lp1(M))θ=Lp(M)and(Hp0(A),Hp1(A))θ⊂ Hmin{p0,p1}(A),by Proposition 3.3 in[3],we get(Hp0(A),Hp1(A))θ⊂ Hp(A).Conversely,we choose an integer n such that min{np0,np0}≥ 1. Let x ∈Hp(A). By Theorem 3.4 in[3],for ε>0,there exist xj∈ Hnp(A)(j=1,2,···,n)such that Set f=f1f2···fn.Then f ∈ F0(Hp0(A),Hp1(A))and f(θ)=x.Hence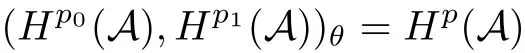


2 Complex Interpolation
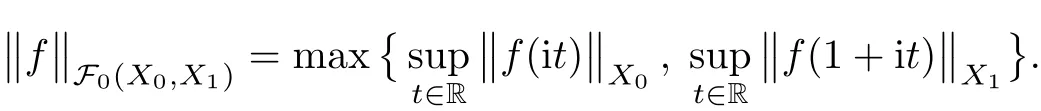
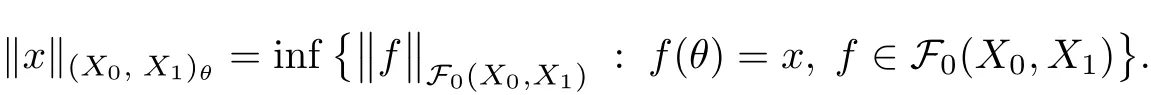

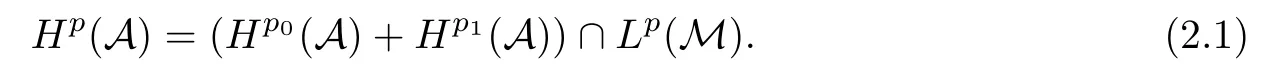


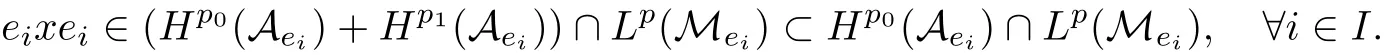




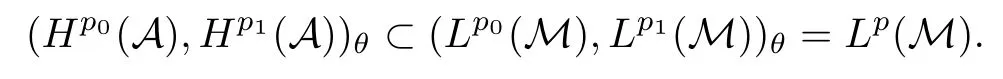


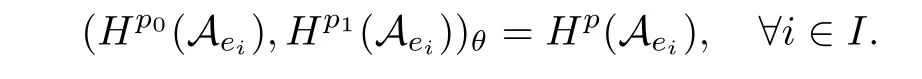
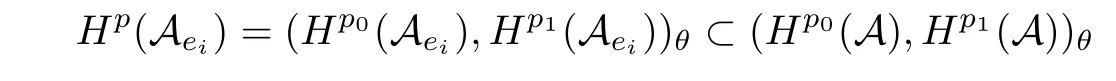
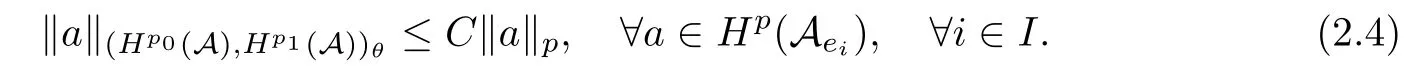


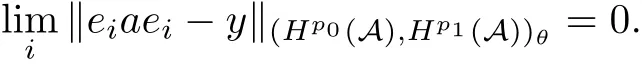

3 Riesz Type Factorization

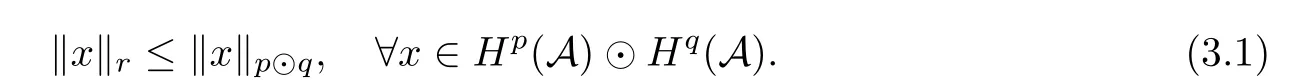

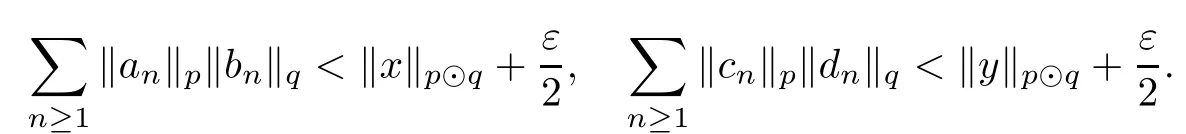



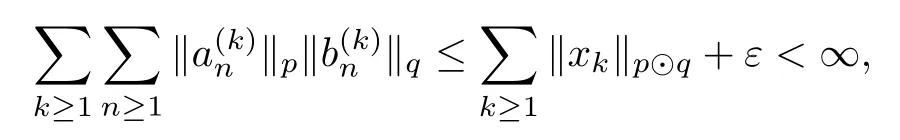
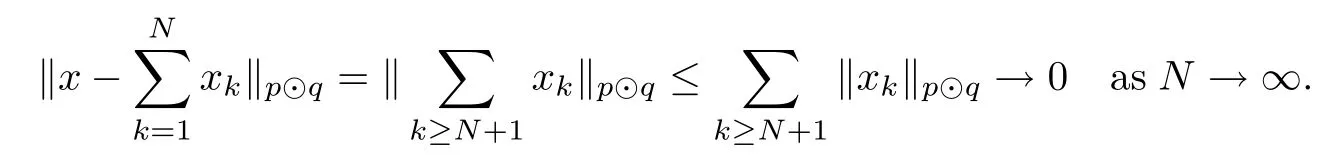


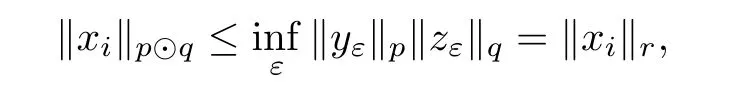



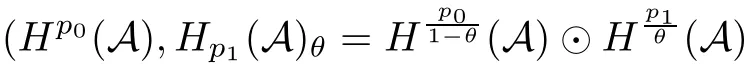
4 Application









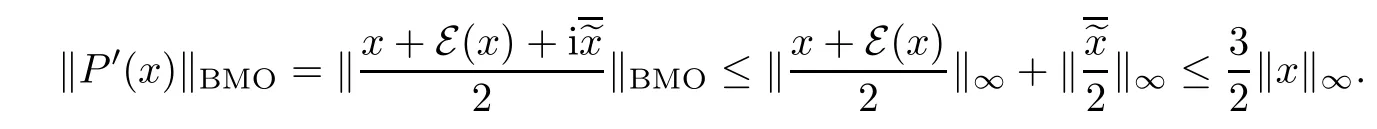




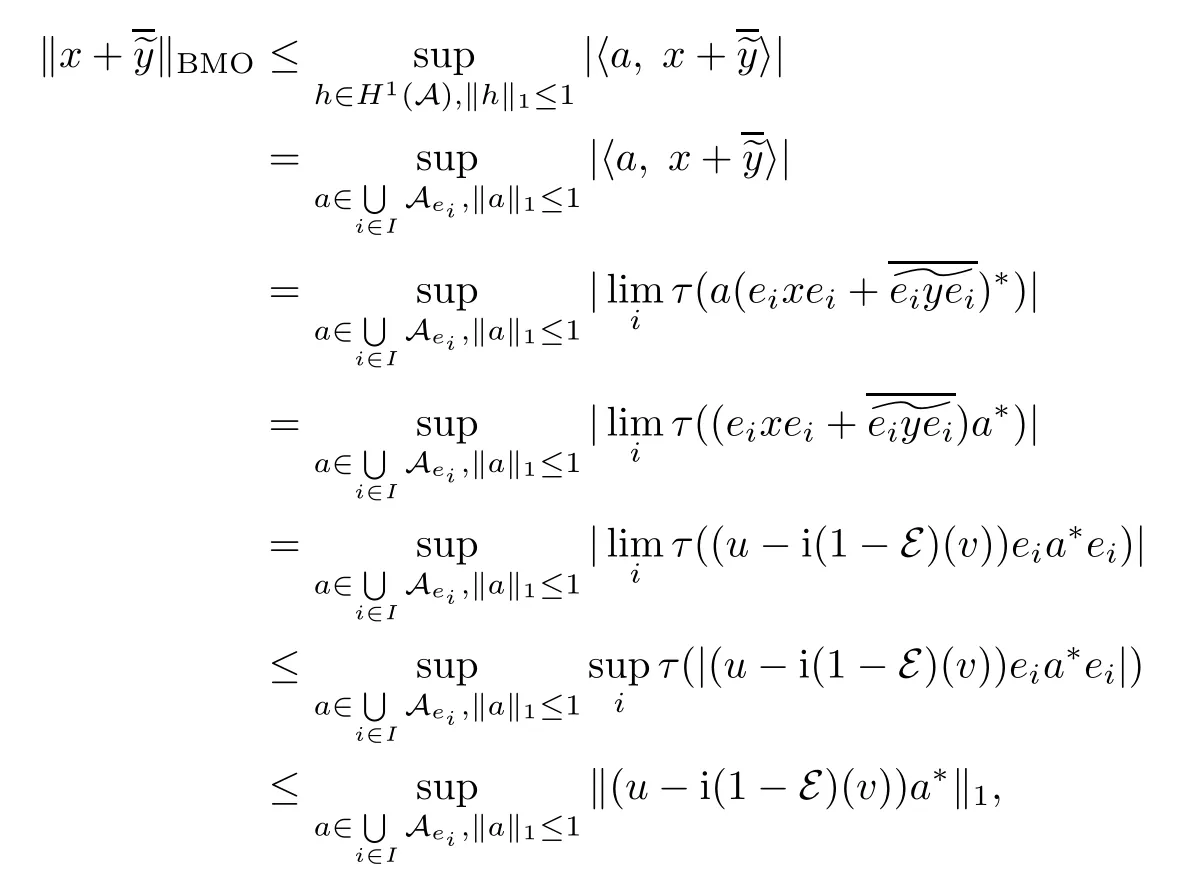




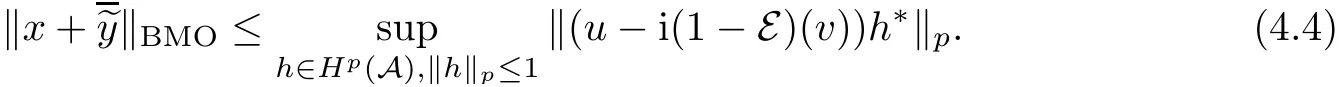






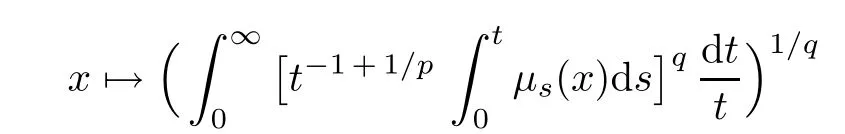

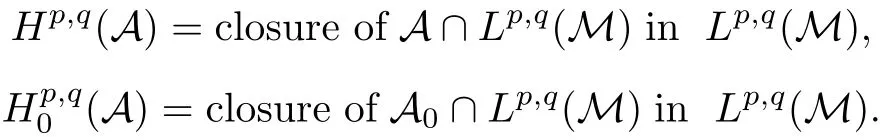




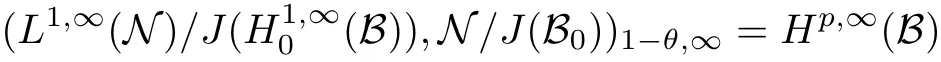




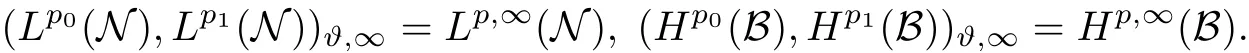



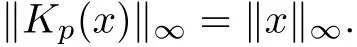



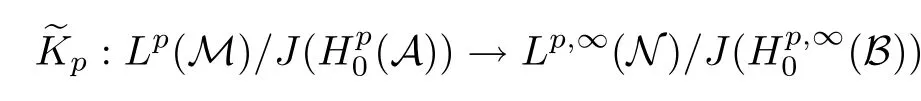

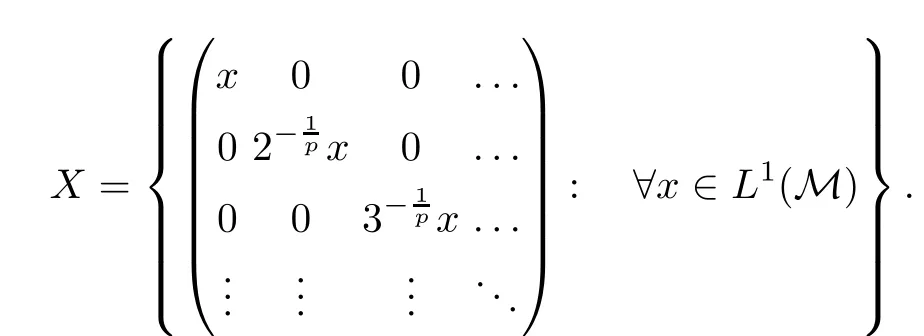

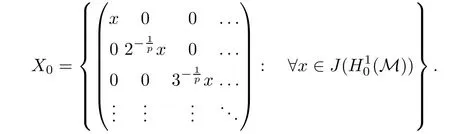






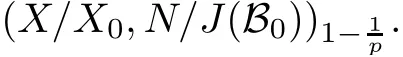
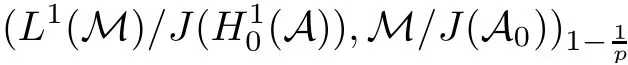


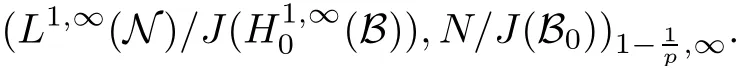
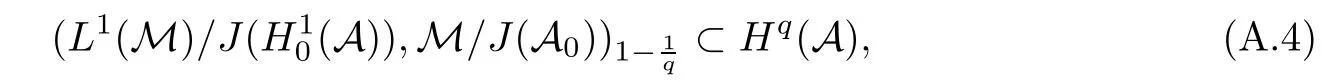
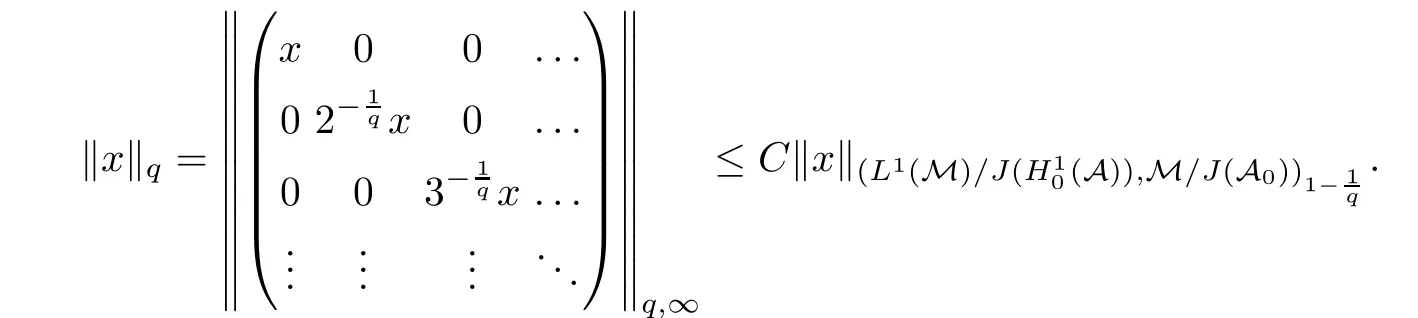


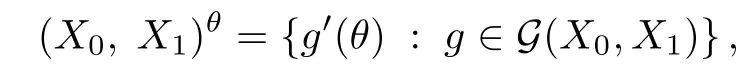
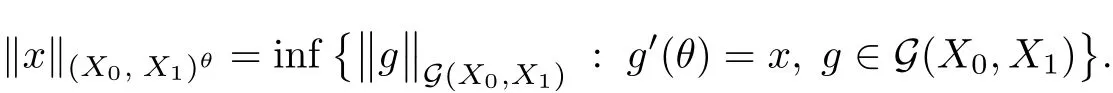



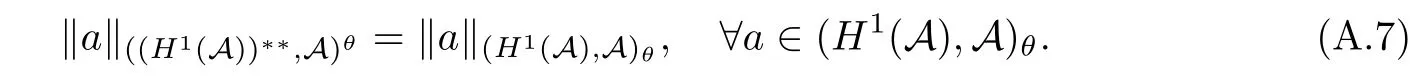



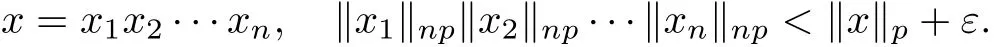
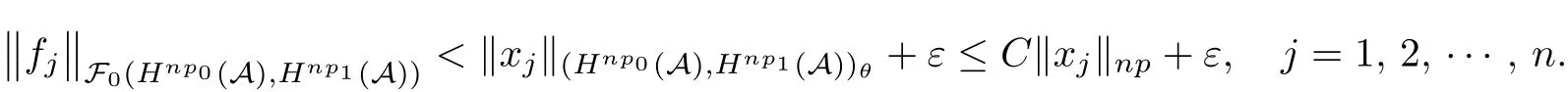

猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- BOUNDEDNESS OF MULTILINEAR LITTLEWOOD-PALEY OPERATORS ON AMALGAM-CAMPANATO SPACES∗
- GLOBAL SIMPLE WAVE SOLUTIONS TO A KIND OF TWO DIMENSIONAL HYPERBOLIC SYSTEM OF CONSERVATION LAWS∗
- THE ENERGY CONSERVATIONS AND LOWER BOUNDS FOR POSSIBLE SINGULAR SOLUTIONS TO THE 3D INCOMPRESSIBLE MHD EQUATIONS∗
- EXISTENCE OF SOLUTIONS OF nTH-ORDER NONLINEAR DIFFERENCE EQUATIONS WITH GENERAL BOUNDARY CONDITIONS∗
- HERMITIAN-EINSTEIN METRICS FOR HIGGS BUNDLES OVER COMPLETE HERMITIAN MANIFOLDS∗
- LOCAL CONVERGENCE OF INEXACT NEWTON-LIKE METHOD UNDER WEAK LIPSCHITZ CONDITIONS∗
