EXISTENCE AND STABILITY RESULTS FOR GENERALIZED FRACTIONAL DIFFERENTIAL EQUATIONS∗
2020-04-27BENMAKHLOUF
A.BEN MAKHLOUF
Department of Mathematics,College of Sciences,Jouf University,Aljouf,Saudi Arabia
Department of Mathematics,Faculty of Sciences of Sfax,Route Soukra,BP 1171,3000 Sfax,Tunisia
E-mail:benmakhloufabdellatif@gmail.com
D.BOUCENNA
Higher School for Professors of Technological Education,Skikda,Algeria
E-mail:mathsdjalal21@yahoo.fr
M.A.HAMMAMI
Department of Mathematics,Faculty of Sciences of Sfax,Route Soukra,BP 1171,3000 Sfax,Tunisia
E-mail:MohamedAli.Hammami@fss.rnu.tn
Abstract In this paper,a sufficient conditions to guarantee the existence and stability of solutions for generalized nonlinear fractional differential equations of order α(1<α<2)are given.The main results are obtained by using Krasnoselskii’s fixed point theorem in a weighted Banach space.Two examples are given to demonstrate the validity of the proposed results.
Key words nonlinear fractional differential equations;stability analysis;generalized fractional derivative;Krasnoselskii’s fixed point theorem
1 Introduction
The development history of the theory of fractional calculus has more than three hundred years[14,24].As an extension of the integer-ordercalculus,the fractional calculus has its unique advantages,such as merits of memory and hereditary properties[5].Since practical problems are described more accurately by fractional-order derivatives than integer-order derivatives,so that they are valuable in various fields,such as dynamics of fl uid mechanics[9,17,27],dielectric polarization[26],bioengineering[19],viscoelasticity[25],etc.Particularly,stability analysis is one of the most fundamental issues for systems.In this few years,there are many results about the stability of fractional order systems[2–4,6,10,11,18,20–23].
A generalized fractional derivative was recently proposed in[13],which generalizes the concept of Caputo and Caputo-Hadamard fractional derivatives.A numerical method was given in[1]for 0<α<1 and Chaos analysis and asymptotic stability of generalized fractional differential equations were given in[2].
In[11],Ge and Kou investigated the stability of the solutions of the following nonlinear Caputo fractional differential equation

whereCDαx is the standard Caputo’s fractional derivative of order 1< α <2.By employing the Krasnoselskii’s fixed point theorem in a weighted Banach space,the authors obtained stability results.
In this paper,we are interested in the problems of qualitative theory analysis of the stability of the solutions for the generalized fractional differential equations.Motivated by the works mentioned above,we concentrate on the existence and stability of the solutions for the generalized nonlinear fractional differential equations

where 1<α<2,ρ>0,ρ 6=1,x0,x1∈R and f:[t0,+∞)× R→ R is a continuous function and f(t,0)=0,∀t≥ t0.
To prove the existence and stability of the solutions,equations(1.1)–(1.2)is transformed into an integral equation and then the Krasnoselskii’s fixed point theorem is used.The obtained integral equation is the sum of two mappings,one is a contraction and the other is compact.
The rest of the paper is organized as follows.In Section 2,preliminaries and useful de finitions are introduced.In Section 3,we give and prove our main results.To show the efficiency of the proposed approach,two examples are presented in the last section.
2 Preliminaries
In this section,let us revisit some basics of the fractional calculus.We adopt the notations of the generalized fractional integral and derivative from[1,13].
De finition 2.1(Generalized fractional integral) Let u∈L1[a,b].The generalized fractional integralu(t)is de fined by

De finition 2.2(Generalized fractional derivative) The generalized fractional derivative of a function u∈ACn[a,b]is de fined by
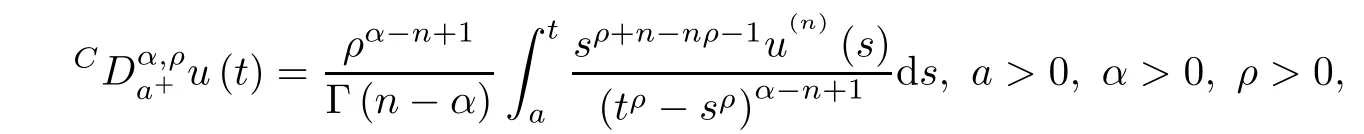
where n be the smallest integer greater than α.
Lemma 2.3Let 1<α<2.The following relationship holds

ProofWe have

Lemma 2.4Let r∈ C([t0,+∞),R),1< α <2 and ρ>0,ρ 6=1.If x is a solution of the fractional initial value problem

then x is a solution of the fractional integral equation

ProofAssume that x is a solution of initial value problem(2.1)–(2.2).From Lemma 2.3,we have

We use integration by parts,we get
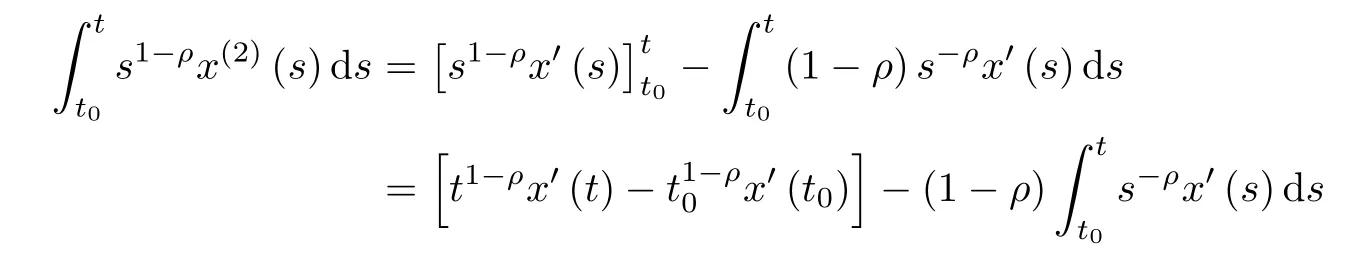
and

Using the Leibniz integral law,we obtain

Then

Hence

By the variation of constants formula,we get

De finition 2.5The function x is called a mild solution of(1.1)–(1.2)if it satis fies

De finition 2.6The generalized nonlinear FDEs(1.1)–(1.2)is said to be stable in Banach space E,if for every ǫ>0 there exists δ:= δ(ε)>0 such that|x0|+|x1|< δ implies that there exists a mild solution x(t)de fined on[t0,+∞)and satis fies kxk≤ ε.
Now,in order to give a result on the stability of the problem(1.1)–(1.2),we will introduce a Banach space.
Let ρ >0,ρ 6=1,1< α <2 and g:[t0,+∞)→ R+such that for all t,s≥ t0,g(t)≥ tαρ2+3and??g(s)≤g(t).Let

Note that E is a Banach space equipped with the norm.For more properties of this Banach space,see[8].
Lemma 2.7Let ρ >0,,1< α <2.Then there exist M1=M1(t0,α,ρ)>0,1>M2=M2(ρ)>0,M3=M3(α,ρ)>0 such that for all t≥ t0,we have

where

ProofLet ρ >0,and 1< α <2,we have two cases.
Case 1For ρ∈(0,1),we have

and

Case 2For ρ>1,we have

and

Lemma 2.8(see[16]) Let Ω be a non-empty closed convex subset of a Banach space(S,).Suppose that A and B map Ω into S such that
(i)A(x)+B(y)∈Ω for all x,y∈Ω,
(ii)A is continuous and AΩ is contained in a compact set of S,
(iii)B is a contraction with constant l<1.
Then there is a x∈Ω with Ax+Bx=x.
In order to prove(ii),the following modi fied compactness criterion is needed.
Lemma 2.9(see[15]) Let F be a subset of the Banach space E.Then F is relatively compact in E if the following conditions are satis fied
3 Main Results
In this section,we shall present and prove our main results.
Theorem 3.1Let 1< α <2,ρ >0,.Suppose that there exist constants η >0,β1>0,and a continuous function ψ :R+× (0,η]→ R+such that

for all t≥ t0,0<|y|≤ η,

holds for every 0 (i)the generalized nonlinear FDEs(1.1)–(1.2)is stable in Banach space E; (ii)the generalized nonlinear FDEs(1.1)–(1.2)has at least one mild solution such that Proof(i)Let 0< ε< η,takewe will prove that if|x0|+|x1|<δ then there exists a mild solution x(t)de fined on[t0,+∞)and satis fies< ε. Consider the non-empty closed convex subset We de fine two mappings A,B on F(ε)as follows Obviously,for x ∈ F(ε),both Ax and Bx are continuous functions on[t0,+∞). For x ∈ F(ε)by(3.1)–(3.2),for any t≥ t0,we have Then On the other hand,there exists M4=M4(t0,α,ρ)such that From(2.6),(2.7),(3.6),we get Then AF(ε)⊂ E and BF(ε)⊂ E.Next,we shall use Lemma 2.8 to prove there exists at least one fixed point of the operator A+B in F(ε).Here,we divide the proof into three steps. Step 1We will prove that Ax+By ∈ F(ε)for all x,y ∈ F(ε). Let x,y ∈ F(ε),from(3.5),(3.7),we obtain which implies that Ax+By ∈ F(ε)for all x,y ∈ F(ε). Step 2We will prove that A is continuous and AF(ε)is a relatively compact in E. First,we will show that A is continuous.Let(xn)n∈Nbe a sequenc such that xn→ x in F(ε).Using(3.1),we get It follows from(2.8)that for any t≥t0, Then We have for any τ≥ t0, so then since f is continuous in[t0,+∞)×R.Thus,it follows from the dominated convergence theorem,that→0 as n→+∞.Therefore A is continuous. Second,we will prove that AF(ε)is a relatively compact in E.From(2.8)it follows that there exists a constant M3=M3(α,ρ)such that for all t≥ t0, And for any T ≥ t0,the fonctionis uniformly continuous on For any x ∈ F(ε)and for any t1,t2∈ [t0,T],t1 as t2→t1which means that,is equicontinuous on any compact interval of[t0,+∞).By Lemma 2.9,in order to show that AF(ε)is a relatively compact set of E,we only need to prove thatis equiconvergent at in fi nity.From(2.8),we have Step 3We claim that B:F(ε)→ E is a contraction mapping. In fact,for any x1,x2∈ F(ε)from(2.7),it follows that By Lemma 2.7,we know that there exists at least one fixed point of the operator A+B in F(ε),which is a mild solution of(1.1)–(1.2).Then the generalized nonlinear FDEs(1.1)–(1.2)is stable in Banach space E. (ii)For any 0< ε< η,de fining We will prove that Ax+By∈ F∗(ε)for any x,y∈ F∗(ε),i.e.,→0 as t→+∞. By the fact that,g(t)≥ tαρ2+3,we obtain and Moreover,we have Let consider the following cases. Case 1If ρ∈(0,1),we have Morever,there exists T2>T1such that for t≥T2, Then,for t≥T2,we obtain Case 2If ρ>1,we have Moreover,there exists T2>T1such that for t≥T2, Then for t≥T2,we obtain Basing in the previous cases,we obtain Using(3.8),we get By(3.9)–(3.12)we get, Thus,there exists at least one mild solution of(1.1)–(1.2)such that Example 4.1Let us consider the following nonlinear fractional differential equation Let g(t)=t9and We have Take We obtain and Then there exists η>0,such that Example 4.2Let us consider the following nonlinear fractional differential equation Let g(t)=t10and We have Take We obtain and Then there exists η>0 such that In this paper,the existence and stability of the solutions for the generalized nonlinear fractional differential equations is investigated.Indeed,the main results are obtained by using Krasnoselskii’s fixed point theorem in a weighted Banach space.Two illustrative examples are presented to show the validity of the suggested results.



























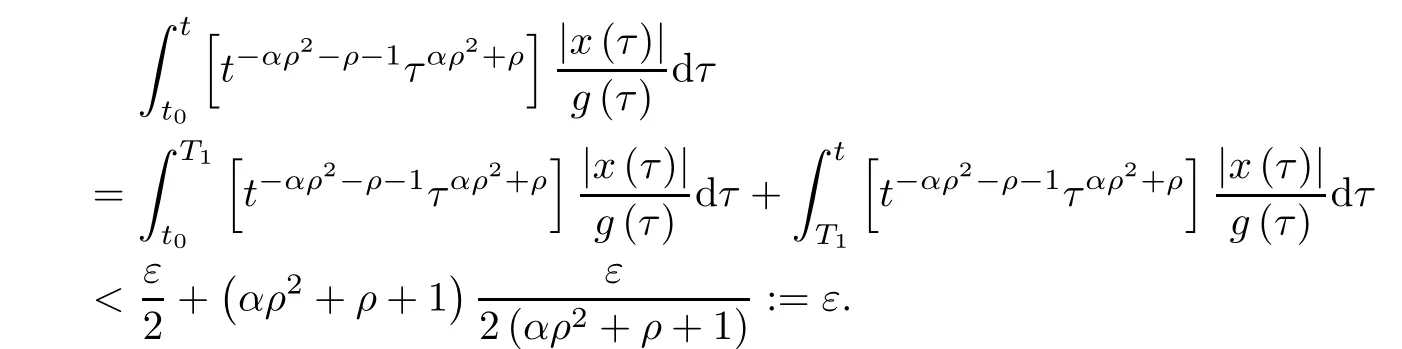








4 Examples







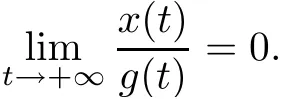

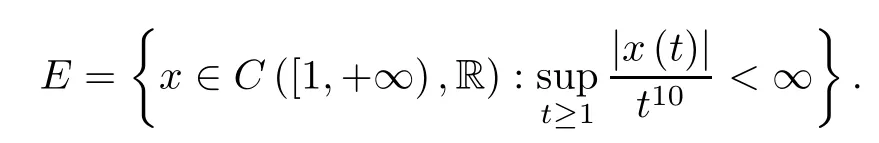





5 Conclusion
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- HILBERT PROBLEM 15 AND NONSTANDARD ANALYSIS(I)∗
- INFINITELY MANY SOLITARY WAVES DUE TO THE SECOND-HARMONIC GENERATION IN QUADRATIC MEDIA∗
- COMPLEX SYMMETRIC TOEPLITZ OPERATORS ON THE UNIT POLYDISK AND THE UNIT BALL∗
- THE BOUNDEDNESS FOR COMMUTATORS OF ANISOTROPIC CALDER´ON-ZYGMUND OPERATORS∗
- GROUND STATES FOR FRACTIONAL SCHR¨ODINGER EQUATIONS WITH ELECTROMAGNETIC FIELDS AND CRITICAL GROWTH∗
- MULTIPLE JEEPS PROBLEM WITH CONTAINER RESTRICTION∗
