THE BOUNDEDNESS FOR COMMUTATORS OF ANISOTROPIC CALDER´ON-ZYGMUND OPERATORS∗

Jinxia LI(李金霞) Baode LI(李宝德) Jianxun HE(何建勋)†

1.School of Mathematics and Information Sciences,Guangzhou University,Guangzhou 510006,China

2.College of Mathematics and System Science,Xinjiang University,Urumqi 830046,China

E-mail:1083853781@qq.com;baodeli@xju.edu.cn;hejianxun@gzhu.edu.cn

Abstract Let T be an anisotropic Calder´on-Zygmund operator and ϕ :Rn × [0, ∞) →[0,∞)be an anisotropic Musielak-Orlicz function with ϕ(x,·)being an Orlicz function and ϕ(·,t)being a Muckenhoupt A∞(A)weight.In this paper,our goal is to study two boundedness theorems for commutators of anisotropic Calder´on-Zygmund operators.Precisely,when b∈BMOw(Rn,A)(a proper subspace of anisotropic bounded mean oscillation space BMO(Rn,A)),the commutator[b,T]is bounded from anisotropic weighted Hardy space(Rn,A)to weighted Lebesgue space (Rn)and when b∈BMO(Rn)(bounded mean oscillation space),the commutator[b,T]is bounded on Musielak-Orlicz space Lϕ(Rn),which are extensions of the isotropic setting.

Key words expansive dilation;Muckenhoupt weight;weighted Hardy space;Calder´on-Zygmund operator;commutator

1 Introduction

The commutator of Calder´on-Zygmund operator T and a function b ∈(Rn),which acts on functions f with satisfying smooth and compactly support properties,is de fined by

which has been studied by many authors,whereis the set of all locally Lebesguemeasurable functions f on Rnthat satisfy,for any compact subset E of Rn.

As we all know,it has important applications in the estimates of the solutions for the elliptic equations and some nonlinear PDEs;see[9,10,17].

For the unweighted situations,a classical result was that Coifman et al.[13]presented the commutator[b,T]is bounded from Lp(Rn)to itself with p∈(1,∞),where b∈BMO(Rn)and T is the classical Calder´on-Zygmund operator.Then,Harboure et al.[21,Theorem(3.1)]proved that[b,T]is bounded from H1(Rn)to L1(Rn)if and only if b equals to a constant almost everywhere.Lately,Ky[23]discovered the largest subspace of H1(Rn)with satisfying that all the commutators[b,T]are bounded from this subspace to L1(Rn).For the weighted situations,´Alvarez et al.[1]showed that the commutator[b,T]is bounded on weighted Lebesgue space(Rn)with b∈BMO(Rn),p∈(1,∞)and w∈Ap(Rn).Moreover,Liang et al.[25]acquired that the commutator[b,T]is bounded from(Rn)to(Rn)if and only if b∈BMOw(Rn),where T is any δ-Calder´on-Zygmund operator with δ∈ (0,1].

For the anisotropy property,we can express it by a general discrete group of dilations{Aj:j ∈ Z}with A being an n × n matrix and all its eigenvalues λ satisfying|λ|>1 in mathematics.For the function spaces,Birnbaum-Orlicz[6]and Orlicz[30]obtained the Orlicz space which is a generalization of Lp(Rn)de fined by an Orlicz function.Moreover,the theory of weighted Hardy spaces on Rnwas studied by Garc´ıa-Cuerva[18]and Strömberg-Torchinsky[31].Calder´on and Torchinsky introduced the study of Hardy spaces on Rnrelated to anisotropic dilations[8,14,15].Bownik[3]lately developed the Hardy spaces theory,which relates to expansive dilations.Moreover,many authors also studied the(weighted)anisotropic product Hardy spaces;see[5,16,26].

Therefore,for the important[b,T],we give that[b,T]still have the corresponding boundedness theorems on the signifi cant function spaces(Rn,A)and Lϕ(Rn).Precisely,when b ∈ BMOw(Rn,A)and T is an anisotropic Calder´on-Zygmund operator,[b,T]is bounded from(Rn,A)to(Rn)(see Theorem 2.8 below),which is an extension of Liang et al.[25,Theorem 1.3].Different from Liang et al.[25,Theorem 1.3],the sufficiency of Theorem 2.8 below is still an open problem,because the Riesz characterisation of the classical Hardy spaces is used in the sufficient proof of Liang et al.[25,Theorem 1.3]while this is still open in the anisotropic setting.Moreover,when b ∈ BMO(Rn)and T is an anisotropic Calder´on-Zygmund operator,combining Theorem 2.8 below and an interpolation theorem given in Li et al.[27,Theorem 2.5],we obtain that[b,T]is bounded on Lϕ(Rn)(see Theorem 2.10 below).

Even noteworthy is that the classical dyadic cubes do not match with the anisotropic dilation,thus a kind of general dyadic cubes of Christ[7]and a class of general dyadic maximal function(see Lemma 3.4 below)are brought in,which are crucial in the proof of Theorem 2.8.Moreover,it is even worth mentioning that,as a key lemma for Theorem 2.8,i.e.,Lemma 3.6,whose proof is different from that of[25,Lemma 2.3],because the John-Nirenberg inequality[22,Lemma 1]is used there while this is still unknown in the anisotropic setting and,luckily,resorting to a signifi cant weighted estimate for dyadic maximal function and anisotropic sharp maximal function from[5,Lemma A.7]and some other subtle estimates,we can only obtain Lemma 3.6.

For the paper,in Section 2,some de finitions such as expansive dilations,anisotropic Muckenhoupt weights and anisotropic Musielak-Orlicz functions and so on are firstly recalled,then two boundedness theorems of the commutator[b,T]are stated.Finally,the proofs of our main results are given in Section 3.

Throughout the whole paper,assume that C is a positive constant which is irrelevant to the main parameters,but it may mean different constants in different lines.DF denotes D≤CF.D∼F means DF and FD.If we give no special illustrations,X is the simply symbol of any space X(Rn)and X(A)is the simply symbol of any space X(Rn;A).

2 Preliminaries and Main Results

In the section,recall the concept of expansive dilations on Rnfirstly,that is,an n×n matrix A is known as an expansive dilation,for convenience a dilation,if|λ|>1,where σ(A)is the collection of all eigenvalues of A(see[3,p.5]).Suppose that λ−and λ+are two positive numbers and satisfy the following condition

In particular,if A is diagonalizable over C,we can select λ−:=min{|λ|: λ ∈ σ(A)}and λ+:=max{|λ|: λ ∈ σ(A)}.Or else,we should take them sufficiently close to these equalities in the light of what we need in the paper.

Lemma 2.2 of[3,p.5]showed that,for a fixed dilation A,we have a number r∈(1,∞)and a set∆:={x∈Rn:|Px|<1},where P stands for some non-degenerate n×n matrix,so that∆ ⊂ r∆ ⊂ A∆,and by a scaling,one can additionally suppose|∆|=1,where|∆|means the n-dimensional Lebesgue measure of∆.Set Bk:=Ak∆ for k∈Z.It is obvious that Bk⊂rBk⊂Bk+1and|Bk|=bkwith b:=|detA|.Suppose that σ is the minimum positive integer satisfying 2B0⊂Bσand,for∀i,j∈Z with i≤j,we have

where E∁:=RnE and E+F is the algebraic sum{x+y:x∈E,y∈F}of any subsets E,F of Rn.

The concept of the homogeneous quasi-norm with respect to A below is fundamental,which shows anisotropic property and was introduced in[3,p.6,De finition 2.3].

De finition 2.1A homogeneous quasi-norm,which relates to an expansive matrix A,is a Borel measurable mapping ρA:Rn→ [0,∞),for convenience,write it as ρ,satisfying the conditions below

(i) ρ(x)∈ (0,∞)for∀ x ∈ Rn{0n}with 0n:=(0,···,0);

(ii) ρ(Ax)=bρ(x)for∀ x ∈ Rn;

(iii) ρ(x+y)≤ H[ρ(x)+ρ(y)]for∀ x,y ∈ Rn,where constant H ∈ [1,∞)is irrelevant to x,y.

When A:=2In×nand ρ(x):=|x|nfor∀ x ∈ Rn,it is easy to see that this is an example of homogeneous quasi-norms associated to A.Since we have known that all homogeneous quasinorms associated to A are equal to each other(see[3,p.6,Lemma 2.4]).Therefore,here and hereafter,we always write the step homogeneous quasi-norm ρ associated to A as the following form,for∀x∈Rn,

From(2.1),it follows that,for∀x,y∈Rn,

In addition,(Rn,ρ,dx)is a homogeneous type space(see[11,12]).

De finition 2.2We say that a function w:Rn→ [0,∞)satis fies the anisotropic Muckenhoupt condition Aq(A)with q∈[1,∞),simply write it as w∈Aq(A),if there is a constant C>0 so that

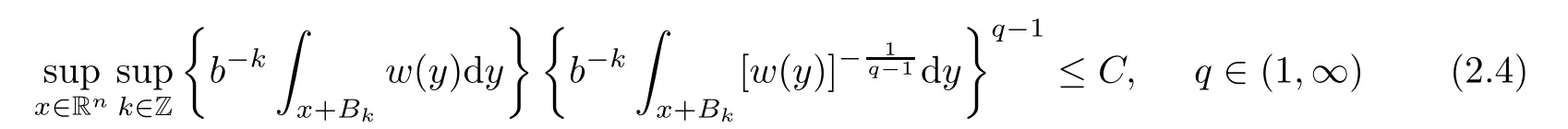
and

It is apparent that q(w)∈[1,∞).From this,we conclude that w/∈Aq(w)(A)and there is a w ∈ (∩r>1Ar(A))A1(A)satisfying q(w)=1(see[28]).

Suppose that ϕ is a nonnegative function on Rn× [0,∞).We call ϕ a Musielak-Orlicz function if,∀ x ∈ Rn,ϕ(x,·)is an Orlicz function on[0,∞)and,∀ t∈ [0,∞), ϕ(·,t)satis fies the measurable property on Rn.Here we call that a function Φ :[0,∞)→ [0,∞)is an Orlicz function,if it satis fies the nondecreasing property,Φ(0)=0,Φ(t)>0 for t ∈ (0,∞)andΦ(t)= ∞ (see[29]).We point out that,unlike the ordinary situation,such Φ may not be convex.

For an Orlicz function Φ,the property of its growth may be the upper and the lower types of Φ,which is the most useful tool for us to study.More precisely,for p ∈ (−∞,∞),we call that a function Φ is upper(resp.lower)type p,if there is a positive constant C satisfying,∀s∈[1,∞)(resp.s∈(0,1))and t∈[0,∞),

Assume that ϕ is a Musielak-Orlicz function.The Musielak-Orlicz space Lϕfirstly introduced by Musielak[29]is the set of all measurable functions f withRRnϕ(x,|f(x)|)dx<∞ and the Luxembourg-Nakano norm

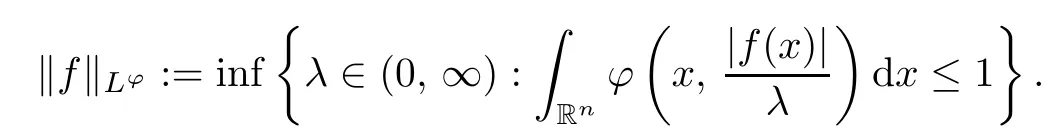
In addition,in this paper,the Musielak-Orlicz functions always satisfy our growth assumptions,which are described as follows.

Assumption(ϕ) Suppose ϕ :Rn×[0,∞)→ [0,∞)is a Musielak-Orlicz function,which satis fies the two conditions below

(1) ∀ t∈ (0,∞),ϕ(·,t)∈ A∞(A);

For a Musielak-Orlicz function ϕ,which satis fies Assumption(ϕ),we have the useful critical index below.Set

Now recall the concept of the(weak)weighted Lebesgue space.Set w∈A∞(A)on Rnand p∈ (0,∞].The weighted Lebesgue spaceis the collection of all measurable functions fsatisfying,when p∈(0,∞),

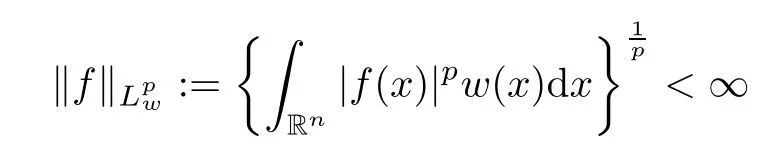
and when p=∞,

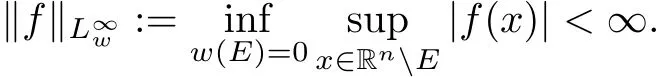
The weak weighted Lebesgue spaceis the collection of all measurable functions fsatisfying

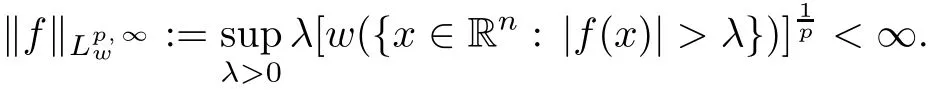
From now on,for any ξ:=(ξ1,...,ξn)∈ Nnwith N:={0,1,2,···},let|ξ|:= ξ1+ ···+ ξn,

For m∈N,let

for φ ∈ S,k ∈ Z and x ∈ Rn,write φk(x):=bkφ(Akx).

For f∈S′and∀x∈Rn,we de fine the non-tangential grand maximal function Mmof f by

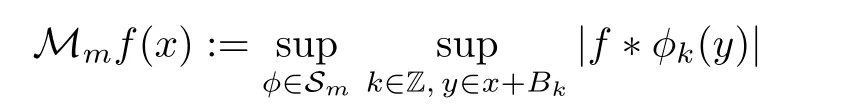
and the radial grand maximal functionof f by

Moreover,by[3,Proposition 3.10],we have the non-tangential and radial grand maximal functions are pointwise equivalent,namely,

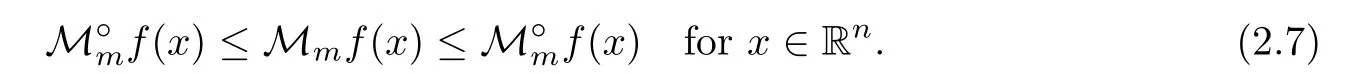
Let

where p∈(0,1],w ∈A∞(A),q(w)is given in(2.5)and⌊a⌋means the maximal integer no more than a,∀a∈R.

The de finition below is from[4,De finition 3.1].

De finition 2.3Assume that∀p∈(0,1],w∈A∞(A),mp,wis given in(2.8)and m∈N satisfying m≥mp,w.We de fine that the weighted anisotropic Hardy space(A)is the collection of all f∈S′with Mmf∈and the(quasi-)norm

∀m1,m2≥mp,w,since(A)=(A)and they have the identical norms(see[4,Theorem 5.5]),hence(A)can be simply written as(A)with m≥mp,w.

Assume that B:={x+Bk:x∈Rn,k∈Z}is the collection of all dilated balls.Forand F⊂Rn,letThe sharp maximal function of f related to dilation A is de fined by,for∀x∈Rn,

In addition,we de fine the anisotropic bounded mean oscillation space BMO(A)by

and

Motivated by Bloom[2,Theorem 1.4(b)]and Liang et al.[25,De finition 1.1],we introduce the de finition below.

De finition 2.4Let w ∈A∞(A)andRRnw(x)/[1+ρ(x)]< ∞.We say that a locally integrable function b is in BMOw(A)if

where xBstands for the center of dilated ball B.

Remark 2.5(i)When A:=2In×n,the space BMOw(A)is reduced to the space BMOwappeared in Liang et al.[25,De finition 1.1].

(ii)BMOw(A)⊂BMO(A)and the inclusion is continuous(see Lemma 3.3 below).

(iii)BMOw(A)is not a trivial function space(see[25,Remark 1.2(ii)]).

We should point out that Bloom[2] firstly thought about the space BMOwwhile researching the pointwise multipliers of weighted BMO space(see[33]).

Now,the concept of anisotropic Calder´on-Zygmund operator related to dilation A(see[24,De finition 4.1])is useful in our study,we state it as follows.

De finition 2.6We call that a locally integrable function K on Ω :={(x,y)∈ Rn×Rn:x 6=y}is an anisotropic Calder´on-Zygmund kernel(associated with a dilation A and a quasinorm ρ)if there are positive constants C and δ such that

(ii)if(x,y)∈ Ω,x′∈ Rnand ρ(x′− x)≤ b−2σρ(x − y),then

We call that T is an anisotropic Calder´on-Zygmund operator if T is a continuous linear mapping S into S′and extends to a bounded linear operator on L2and,∀f ∈and x 6∈supp(f),Tf has the following form

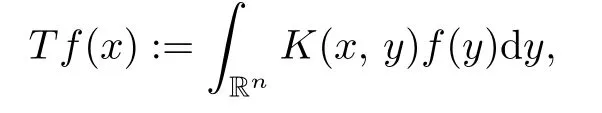
where K is an anisotropic Calder´on-Zygmund kernel.

Remark 2.7(i)When A:=2In×nand ρ(x):=|x|n,∀ x ∈ Rn,the anisotropic Calder´on-Zygmund operators go back to the classical Calder´on-Zygmund operators.

(ii)When A is a diagonal matrix,which has the diagonal terms eα1,eα2, ···,eαnwith α1, α2, ···,αn>0 and α = α1+ α2+ ···+ αn,and ρ is written as ρ(x1,x2,···,xn)=related to A.Then the anisotropic Calder´on-Zygmund operators are also one kind of homogeneous singular integral operators in the sense of Stein[32,Chapter 13.5].

Now,we introduce our two theorems below.

Theorem 2.8Let δ∈ (0,logbλ−],w ∈ A1+δ(A),RRnw(x)/[1+ρ(x)]dx< ∞,b∈BMOw(A)and T be an anisotropic Calder´on-Zygmund operator which is given in De finition 2.6.Then the commutator[b,T]is bounded from H1w(A)to L1w.

Remark 2.9When A:=2In×nand ρ(x):=|x|n,∀ x ∈ Rn,Theorem 2.8 goes back to[25,Theorem 1.3].

Theorem 2.10Let b∈BMO(A),ϕ be a Musielak-Orlicz function which satis fies Assumption(ϕ),RRnϕ(x,t)/[1+ ρ(x)]dx< ∞ and ϕ(·,t)∈ A1+δwith δ∈ (0,logbλ−]uniformly,∀ t∈ (0,∞),and q(ϕ)be given in(2.6)with[q(ϕ)]2<≤< ∞ and let T be an anisotropic Calder´on-Zygmund operator as in De finition 2.6.Then the commutator[b,T]is bounded on Lϕand,in addition,there is a positive constant C such that,for any f∈Lϕ,

3 Proofs of Main Results

To show Theorem 2.8,the de finition below is necessary,which comes from[4,De finition 3.2].

De finition 3.1Let w∈A∞(A),q(w)and mp,wbe given in(2.5)and(2.8),respectively.We call that a triplet(p,q,s)wis admissible,if p∈(0,1],q∈(q(w),∞]and s∈N with s≥mp,w.Meanwhile,a function a on Rnis called a(p,q,s)w-atom if it satis fies the three conditions below

(i)suppa⊂x0+Bjfor certain j∈Z and x0∈Rn;

(iii)R

The lemma below comes from[31,pp.7–8].

Lemma 3.2Let q∈[1,∞)and w∈Aq(A).Then∀x∈Rn,k∈Z and E⊂x+Bk∈B,there are two positive constants C1and C2such that

Inspired by Liang et al.[25,Proposition 2.1],we have the lemma below.

Lemma 3.3Let w ∈A∞(A).Then,there is a positive constant C such that,∀f∈BMOw(A)and B∈B,

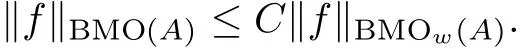
ProofTo show the lemma it suffices to prove that,∀f∈BMO(A)and xj+Bj∈B with∀xj∈Rnand j∈Z,

Obviously,it suffices to prove

From Lemma 3.2 with w ∈ Aq(A)and q>q(ϕ),it follows that

This shows kfkBMO(A).kfkBMOw(A)and hence we complete the proof of Lemma 3.3.

Now we recall the dyadic cubes.It is also known to us that(Rn,ρ,dx)is a space of homogeneous(see[11,12]).On the homogeneous space,an analogue of the grid of Euclidean dyadic cubes is provided by the lemma below,which is from[5,Lemma 2.3](see[7]).

Lemma 3.4Let A be a dilation.We have a collection Q:={⊂Rn:k∈Z,α∈Ik}of open subsets,where Ikis some index set,satisfying

(i)|Rn ∪α|=0 for every given k and=if α 6= β;

(ii)for ∀ α,β,k,ℓ with ℓ≥ k,we have=or;

(iii)for every(ℓ,β)and every k< ℓ,we have a unique α satisfying;

(iv)there are some negative integer v and positive integer u satisfying,for∀with k ∈Z and α∈Ik,we have∈such that,∀ x ∈,α+Bvk−u⊂⊂ x+Bvk+u.

In the following,for simplicity,in Lemma 3.4 are called the dyadic cubes and k is called the level of the dyadic cubewith k ∈ Z and α ∈ Ik.Moreover,we write the level as ℓ().

Now we think back to the concept of the dyadic maximal function.∀f∈and x∈Rnwith f being measurable functions,the dyadic maximal function is de fined by

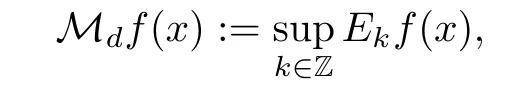
where

and Qk:={:α ∈ Ik}stands for the set of dyadic cubes which are given in Lemma 3.4.

The lemma below is from[5,Lemma A.7].

Lemma 3.5Let p0,p∈[1,∞)with p0≤p,w∈Ap(A)and f∈with Md(f)∈.Then there is a positive constant C,independent of f,such that

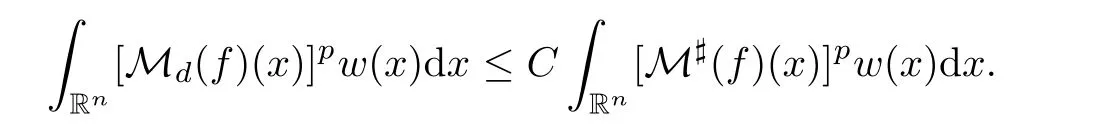
Motivated by Liang et al.[25,Lemmas 2.3 and 2.4],we also have the two lemmas below.

Lemma 3.6Let w∈Aq(A)and q∈[1,∞).Then,there is a positive constant C such that,for∀f∈BMO(A)and∀B∈B,

ProofNotice that,∀f∈ BMO(A)and∀w ∈ Aq(A)with q∈ (1,∞),by the Hölder inequality and(2.4),we have

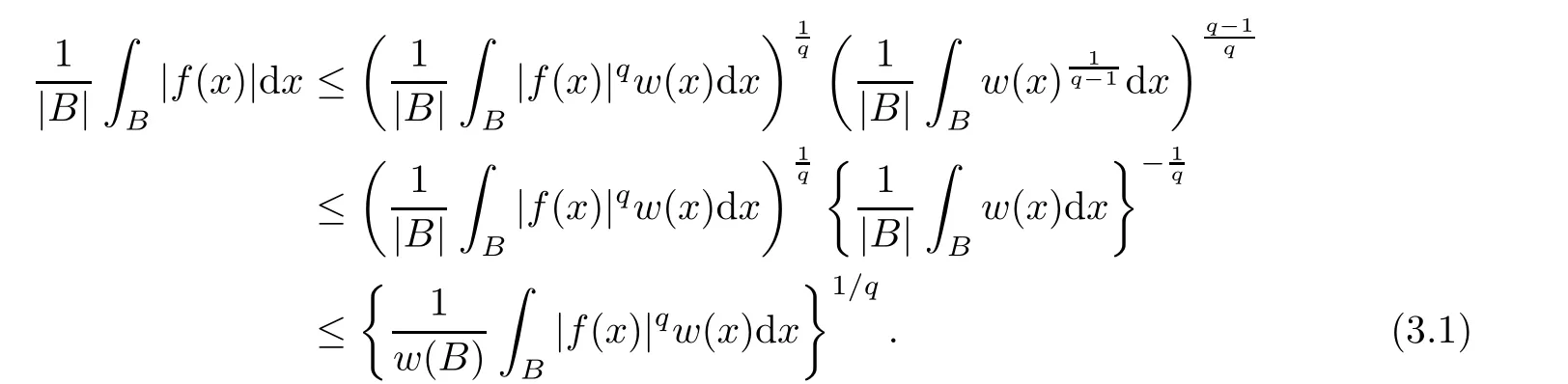
Setting

First,we will prove

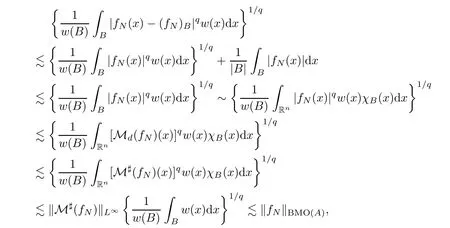
By(3.1),|fN(x)|≤ Md(fN)(x)a.e.(see[5,Proposition A.4(ii)]),wχB∈ Aq(A)with χBbeing the characteristic function of B,and Lemma 3.5 with p0=p=q,we get provided Md(fN)∈by Lemma 3.5.To show this,by the fact that Mdis bounded onwith wχB∈ Aq(A)(see[19,p.423]),it suffices to show that fN∈.Since|fN|≤ N is a locally integrable function,it is easy to get fN∈.

Now,we will show

Since fN→f(N→∞)a.e.x∈B,we have|fN|→|f|(N→∞)a.e.x∈B.From this and the Lebesgue dominated convergence theorem,we conclude that(fN)B→fBand|fN−(fN)B|→|f−fB|(N →∞)a.e.x∈B and hence,|fN−(fN)B|q→|f−fB|q(N →∞)a.e.x∈B.By this and using the Lebesgue dominated convergence theorem again,we obtain that,for a.e.x∈B,

which implies(3.2)holds true.

When q=1,by the Hölder inequality and(3.2)with q=2,we have

which,combining(3.2)with q∈ (1,∞),we finish the proof of Lemma 3.6.

Lemma 3.7Let δ∈ (0,logbλ−],q ∈ (1,1+ δ),w ∈ Aq(A)and T be an anisotropic Calder´on-Zygmund operator given in De finition 2.6.Then, ∀ b ∈ BMOw(A)and(1,q,0)watom a associated with the dilated ball B∈B,there is a positive constant C such that

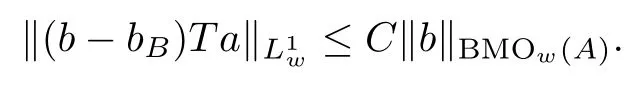
ProofSet B:=x0+Bjand B∗:=x0+Bj+4σ,∀ x0∈ Rnand j∈ Z.We only need to prove that

and

By repeating the proof of[25,Lemma 2.4],we obtain that I1.kbkBMOw(A).Next,we turn to show the estimate of I2.

∀ y∈ x0+Bjand x ∈ x0+Bj+4σ+kBj+4σ+k−1with k∈ Z+,x0∈ Rnand j∈ Z,by(2.1)and(2.2),we get y − x ∈ Bj+Bj+4σ+kBj+4σ+k−1⊂ Bj+5σ+kBj+3σ+k−1,which implies that ρ(y − x) ≥ bj+3σ+k−1.Assume δ+1 − q>0.By Fubini’s theorem,De finition 2.6(ii),ρ(y − x)&bj+5σ+k−1,ρ(x0− y)≤ bj,Hölder’s inequality,De finition 3.1(ii),(2.4),Lemma 3.6,|bx0+Bj+5σ+k− bB|.kkbkBMOw(A),∀ k ≥ 1 and Lemmas 3.6,3.2 and 3.3,we have

which,together with the estimate of I1and Lemma 3.3,completes the proof of Lemma 3.7.

The lemma below is on account of Bownik et al.[4,Theorem 7.2].

Lemma 3.8Let A be an expansive dilation,w∈A∞(A),0

Then we have a unique bounded linear operatorfrom(Rn;A)to X which extends T.

Motivated by the techniques of[20,Theorem 2.8]and[24,Theorem 4.7],we obtain the lemma below,the proof of which is omitted here.

Lemma 3.9Let p1∈ (0,1],w ∈ A1+δ(A)with δ∈ (0,logbλ−]and T be an anisotropic Calder´on-Zygmund operator given in De finition 2.6.Then T can be extended to a bounded linear operator from(A)to.

Now,let us prove Theorem 2.8.

Proof of Theorem 2.8Since w ∈ A1+δ(A)with δ∈ (0,logbλ−],we have q ∈ (1,1+δ)satisfying w∈Aq(A).From Lemma 3.8,for any continuous(1,∞,0)w-atom a associated with the dilated ball B:=x0+Bj∈B,we only need to show that,

From this,(2.7),Lemma 3.7 and the boundedness property of T from(A)to(see Lemma 3.9 with p1=1),it follows that we only need to prove

For B,let B∗:=x0+Bj+4σ.For∀ x∈ (B∗)∁and y∈ B,by(2.1)and(2.2),we can obtain x−x0∈and y−x0∈Bj,hence we have y−x∈+Bj⊂,which implies ρ(y −x)≥ bj+3σ.From this and ρ(x0− y)≤ bj,we conclude that ρ(y −x)≥ ρ(x0−y).Thus,by(2.3),we get

From this,it follows that

Hence,by φk(x):=bkφ(Akx)and De finition 2.1(ii),we further obtain

From this,De finition 3.1(ii)with p=1 and q= ∞ and the Hölder inequality,it follows that

In addition,by using the Hölder inequality,the boundedness property ofonsatisfying q∈ (1,1+δ)(see[4,De finition 2.10 and Proposition 2.11(ii)]),De finition 3.1(ii)and Lemmas 3.6 and 3.3,we have

Consequently,the proof of Theorem 2.8 is completed.

In order to show Theorem 2.10,the lemmas below are necessary.

Inspired by´Alvarez et al.[1],we get the lemma below,whose proof is omitted.

Lemma 3.10Let b∈ BMO(A),p∈ (1,∞),ϕ be a Musielak-Orlicz function which satis fies Assumption(ϕ),RRnϕ(x,t)/[1+ρ(x)]dx< ∞ and ϕ(·,t)∈ A1+δ(A)with δ∈ (0,logbλ−]uniformly for ∀ t ∈ (0,∞)and T be an anisotropic Calder´on-Zygmund operator given in Definition 2.6.Then the commutator[b,T]is bounded onand,in addition,there exists a positive constant C such that,for∀f∈and t∈ (0,∞),

The lemma below comes from[27,Theorem 2.5].

Lemma 3.11Let p1∈ (0,1],ϕ be a Musielak-Orlicz function which satis fies Assumption(ϕ),R

Rnϕ(x,t)/[1+ ρ(x)]dx< ∞ and ϕ(·,t)∈ A1+δwith δ∈ (0,logbλ−]uniformly for ∀ t∈(0,∞)and let q(ϕ)be given in(2.6)with[q(ϕ)]2<< ∞ and p2∈ (,∞].Assume that T is a sublinear operator which is de fined on(A)+and satis fies that there are two positive constants C1and C2,∀α∈(0,∞)and t∈(0,∞),

and

with the common alteration when p2=∞.Then T is bounded on Lϕand,in addition,∀f∈ Lϕ,we have a positive constant C satisfying

Now,let us show the proof of Theorem 2.10.

Proof of Theorem 2.10By Lemma 3.10,we obtain,∀ t∈ (0,∞)and p∈ (1,∞),the commutator[b,T]is bounded on.From this,[b,T]is bounded from(A)to(see Theorem 2.8 with w(x)being replaced by ϕ(·,t),∀ t∈ (0,∞))and Lemma 3.11,we conclude that the commutator[b,T]is bounded on Lϕ.Then we finish the proof of Theorem 2.10.