HILBERT PROBLEM 15 AND NONSTANDARD ANALYSIS(I)∗
2020-04-27BangheLI李邦河
Banghe LI(李邦河)
KLMM,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China
E-mail:libh@amss.ac.cn
Abstract Hilbert problem 15 required understanding Schubert’s book.In this book,reducing to degenerate cases was one of the main methods for enumeration.We found that nonstandard analysis is a suitable tool for making rigorous of Schubert’s proofs of some results,which used degeneration method,but are obviously not rigorous.In this paper,we give a rigorous proof for Example 4 in Schubert’s book,Chapter 1. §4 according to his idea.This shows that Schubert’s intuitive idea is correct,but to make it rigorous a lot of work should be done.
Key words Hilbert problem 15;nonstandard analysis;enumeration geometry
1 Introduction
In Schubert’s book[1],Chapter 1. §4,he stated the principle of conservation of number.This principle can be rigorously stated by the language of modern algebraic geometry(see[2])as follows.
Let Γ be a subvariety of dimension r in a nonsingular variety of dimension n,and Γ′be a subvariety of dimension n−r.If the intersection number(counting multiplicities)of Γ′and Γ′is N,and Γ′is a subvariety which is algebraically equivalent to Γ′,then the intersection number of Γ′and Γ′is either in finite,or equal to that of Γ and Γ′.
As applications of this principle,he gave 6 examples.
Example 4Suppose in a fixed plane,there is a 1-dimensional system Σ of planar curves,and a curve C of degree m and rank n,we use this principle to determine the number x of curves in Σ tangent to C.The method is,using a special curve satisfying the de finition of C,to replace general curve C.It is well-known that such a curve can be degenerated to m lines,each of which coincides with a single line g,and its tangent lines form n sets of lines,each consists of all lines passing through a point(called the center of the relevant set),and the set S of the n centers is contained in g.Thus,by the principle of conservation of number,the number x can be determined by studying how many curves in Σ tangent to the above special curve C.For this,we only need to clarify the meaning of“two curves are tangent”,then it will become very easy.“Two curves are tangent” means they have a common point and a common tangent line passing through the point.According to this,there are two cases leading to tangency with special curve C:
1)when a curve in Σ passes through one of the n points in S,this curve is tangent to C once;
2)when a curve in Σ tangents to g,it must tangent to C m times.We say that it is m times,because g is a tangent line of C with multiplicity m.Hence every time of tangent leads to form a figure composed by a tangent line and a tangent point,and there are exactly m identical such figures on C.
Thus,if we useµto denote the number of curves in the system passing through a given point,ν the number of curves which tangent to a given line,there will be the following known formula for x:

So far we have stated Schubert’s proof for Example 4.We see that for this,actually he used the variety consisting of planar curves with degree m and rank n regarded as its points,and taking a point in it which is very near to a point representing a line with multiplicity m in the variety whose points represent planar curves of degree m.So,to make Schubert’s proof rigorous,we need to make the word “near” precisely.That can be done by using nonstandard analysis.
2 Rigorous Proof of Example 4
2.1 Rigorous Description of the System Σ and Relevant Conditions
About the 1-dimensional system Σ,we regard it as a curve in a projective space CPNformed by all curves in the given plane with degree r,equal to the degree of all curves in Σ.
To avoid the de finitions of ν being meaningless,we assume that r ≥ 2 and there are at most finite points on Σ which correspond to reducible curves.This is equivalent to that Σ is not contained in the Zariski closed set in CPNcorresponding to all reducible curves of degree r,or that the intersection of Σ with the Zariski open set corresponding to all irreducible curves of degree r is nonempty.
To describe the dual system Σ′of Σ precisely,we feel that we need to use the concepts of generic point and specialization of van der Waerden[3],developed by Weil[4].In contrast to van der Waerden’s de finition of generic point in some extension field which is not fixed,Weil introduced a fixed field once forever,called universal domain,generic points are de fined on it.Obviously,Weil’s treatment made things easier and more comfortable.
A universal domain K of characteristic zero is an algebraically closed field with in finite degree of transcendency over the sub field of rational numbers.
By a field,it is understood(a)it is a sub field of K;(b)K has in finite degree of transcendency over it.Since Schubert worked on the field C of complex numbers,we assume C is such a field.It is interesting and I believe it is important that the nonstandard extension∗C of C in a polysaturated model(see[5,6])can be taken as a universal domain with C as such a field.First,∗C is algebraically closed.To prove that∗C has in finite degree of transcendency over C,we use the result of[7]which says that there are lots of generic points of any variety V over C in its nonstandard extension∗V,hence what we need follows.
The bene fi t to use∗C as the universal domain is that it has natural topology inheriting from the topology of C,while the general K does not.The nonstandard extension keeps the intuition of“near”,makes “in finitely near” very rigorous.

and denote by Iithe(i1,i2,i3)corresponding to i,XIi=be the relevant monomial.
Let[a0,a1,···,aN]∈ CPNrepresent the curve

and σ =[σ0,σ1,···,σN]∈∗CPNbe a generic point of Σ.Then σ ∈∗Σ,and
have dimension 1 over C(for the de finition of dimension,see[4]p.2).Notice that σ ∈∗Σ is a generic point of Σ over Ciffat least one of,···,andis in∗C−C,in the case of σi6=0.
Let

Then the solutions[x1,x2,x3]∈∗CP2of Fσ(x1,x2,x3)=0 form a curve Cσde fined over the field C(σ).Assume ξ=[ξ1,ξ2,ξ3]is a solution such that some ξi6=0,and one ofandis algebraically independent over C(σ)(its existence is obvious),then ξ is a generic point of Cσover C(σ).
Now,let

Then ξ′is a generic point of the dual curveof Cσover C(σ).Also,let N′=−1 and let CPN′be the space formed by all curves of degree γ′in CP2,where γ′is the degree of,thenis de fined in∗CP2by an equation

where Jj=(j1,j2,j3)and=are de fined similarly as Iiand XIi,such that∈C(σ),j=0,1,···,N′.For σ′=∈∗CPN′,de fine C(σ′)similarly as C(σ).The dimension of C(σ′)over C is less than or equal to 1,since C(σ′)⊂ C(σ).If it is less than 1,then C(σ′)=C.It is well-known that the dual curve ofis Cσ,which would imply C(σ)=C also,a contradiction.Hence the dimension of C(σ′)over C is 1,i.e.,C(σ′)=C(σ),and σ′is a generic point of a curve Σ′⊂ CPN′over C.About the relation of∗Σ′and Σ′,we have the following.
Lemma 2.1(Fundamental Lemma)Let V be an irreducible variety in CPk.Then V has a generic point v in∗CPk,and a point x ∈∗CPkis a specialization of v i ffx ∈∗V.
ProofThe existence of such v is guaranteed by Theorem 1 in[7]:for any p∈V,there is a generic point in the monad M(p)of p in∗V.
Let finite P1,P2,···,Plgenerate IV,the ideal of homogeneous polynomials in C[X0,X1,···,Xk]de fining V.Then x=[x0,x1,···,xk]∈∗CPkis a specialization of v over C i ff
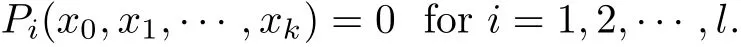
On the other side,we have the sentence:
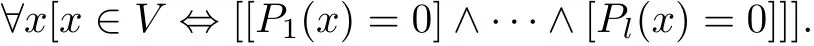
And by the transform principle,we have
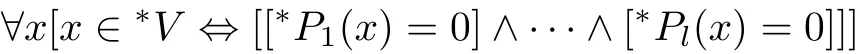
while∗Pi=Pifor i=1,2,···,l.So x ∈∗V is equivalent to x being a specialization of V over C.
(σ,ξ,ξ′) ∈∗CPN×∗CP2×∗CP2has dimension 2 over C,so its all specialization in CPN×CP2×CP2(in∗CPN×∗CP2×∗CP2)over C is a 2-dimensional variety U(∗U).Since ξ and ξ′have also dimension 2 over C,the image of U under the projection p1to the first CP2is the whole CP2,so is under p2to the second CP2.Thus,
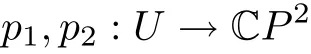
are morphisms of finite degrees.The degree of p1is just Schubert’s µ,and that of p2is ν.Let Ui,i=1,2,be the set of the singular points of U and the nonsingular points at which the map piare degenerate(i.e.,having Jacobian determinant zero).Then pi(Ui)is a Zariski closed set of dimension less than or equal to 1.Therefore,on CP2−p1(U1),every point hasµinverse images under p1,and on CP2−p2(U2),every point has ν inverse images under p2.piis locally biholomorphic on U−Ui,for i=1,2.Furthermore,let
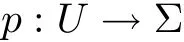
be the natural projection.
We have proved before that C(σ′)=C(σ),which implies that Σ and Σ′are birationally equivalent under the dual map.Now let˜Σ⊂Σ and⊂Σ′be the Zariski open subsets which correspond under the dual map one to one so that 1)the points inandare nonsingular and the corresponding curves are irreducible;2)for,all singularities of the curvesform open curves c1,c2,···,clin CP2,and for any ci,i=1,2,···,l the tangent lines at ci,form open curves,···,in the dual CP2;3)the singularities ofof allform open curves.Next,letbe the union of the curves corresponding to the finite set Σ′−and Notice that a point belonging to anyrepresents a tangent line of higher order or a multiple tangent line of some curve corresponding to a point in˜Σ.Thus Z′is a Zariski closed set in CP2of dimension less than or equal to 1,and a point being in CP2−(Z′∪p2(U2))implies that as a line it can be only a tangent line of a curve corresponding to a point in˜Σ with only one nonsingular point as tangent point,not of higher order.So there are exactly ν different curves in˜Σ with it as a common tangent line.
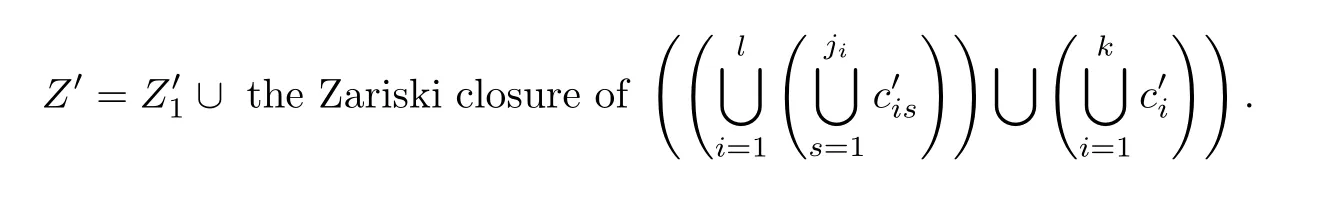
Let Z1be the union of the curves corresponding to the finite set Σ−,and

Then Z is a Zariski closed set of dimension less than or equal to 1,and a point belonging to CP2−(Z∪p1(U1))implies that there are exactlyµelements in Σ which are in˜Σ and each corresponds to a curve passing through it as a nonsingular point.
As Z having dimension less than or equal to 1 implies that the set of lines intersecting with Z at only finite points is a nonempty Zariski open set in the dual CP2,we denote this set by U2.
For the curve C given by Schubert of degree m and rank n,if it is reducible,any its irreducible component must have degree greater than 1 to guarantee n being meaningful.Now let L be a line whose representing point in the dual CP2is in CP2−(Z′∪p2(U2))∩U2.Then,there are exact ν different curves inwith L as a tangent line,and L∩Z has only finite points.
1)the tangent lines of C passing through the points in Z∩L or the tangent points of L as the tangent line of the ν curves in˜Σ;
2)the lines tangent to C at singular points;
3)the lines each of which is tangent to C with higher order or at more than one points;
4)the lines connecting a singular point of C and the tangent points on L of the ν curves as in 1).
Since there are only finite such lines,we can choose a point S∈CP2−?C∪L∪?,such that there are exactly n tangent lines of C passing through S,each of which is tangent at a nonsingular point of C,and the intersection with L is neither in Z nor a tangent point,and any line connecting S and one of the tangent point on L of the ν curves does not pass through any singular point of C.
2.2 Contributions of the Intersections of L and the Tangent Lines of C from S
Choose homogeneous coordinates[x,y,z]such that L is the line y=0,S is the point[0,1,0]and one of tangent lines of C passing through S is x=0 tangent to C at the[0,a,1],and the equation of C is f(x,y,z)=0.Then in a neighborhood of(0,a,1),C is given by
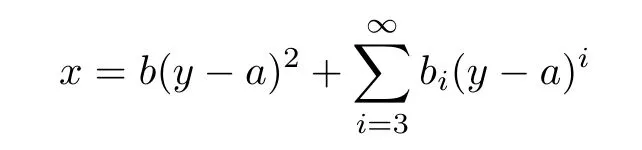
with the series converging.
Let t∈∗C be a nonzero in finitesimal,Ctbe nonstandard curve ⊂∗CP2given by the equation

Then Ctis contained in the in finitesimal neighborhood of the line y=0,i.e.,[1,y,z]or[x,y,1]∈Ctimplies y∈∗C being an in finitesimal,or equivalently,the standard part of any point in Ctis on the standard line y=0.
Assume[0,ai,1],i=1,2,···,s,are the points on C other than[0,a,1],then[0,tai,1],i=1,2,···,s,and[0,ta,1]are the all points of Cton the line x=0.
For any point on C other than the tangent points of the tangent lines from S,if it is nonsingular,its tangent line has the form
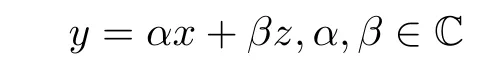
and if it is singular,there may have several tangent lines,each of them should have the above form,too.Thus,for a point on∗C in the monad of a point in C which is not a tangent point of some tangent line of C passing through S,the tangent line of∗C at it should have the form


Especially,at the points of Ctcorresponding to the points on∗C in the monad of[0,ai,1],i=1,2,···,s,the tangent lines have the form

Now,the point[0,0,1]has the property that there are exactlyµpoints in,each of whose corresponding curve passes through it with it as a nonsingular point.For any such point˜σ in,there is a point u in U such that p(u)=,p1(u)=[0,0,1].Let Uube a neighborhood of u in U such that p1:Uu→p1(Uu)is biholomophic and p(Uu)is biholomorphic to a neighborhood W of 0 in C,with 0 corresponding to˜σ.Then in a small neighborhood of[0,0,1]⊂p1(Uu),for small w∈W,the curve corresponding to w has the form

with α(w),β(w),αi(w),i≥ 2 holomorphic functions of w,the series converging,and α(0)= α,β(0)=0,αi(0)= αi,i≥ 2.We claim that the derivative of β(w)at w=0 is nonzero.For,otherwise,for y=0 and small x,

implies there are more than one small w whose corresponding curves pass through one point[x,0,1],contradicts to p:Uu→Σ being well-de fined.
Now,it is clearly from a usual argument in nonstandard analysis that all the curves corresponding to points in∗Σ with w-coordinates in finitesimals,have tangents in the monad of[0,0,1]in∗CP2,whose standard parts are all

And the tangents of the points of Ctin the monad of[0,0,1]corresponding to the points in the monad of[0,ai,1],i=1,2,···,s,all have standard parts

So the curves in∗Σ corresponding to in finitesimal w and the parts of Ctrelevant to[0,ai,1],i=1,2,···,s,cannot tangent in the monad of[0,0,1].Also,the curves corresponding to nonin finitesimal w do not pass the monad of[0,0,1],hence cannot tangent to Ctthere.
Next,we come to prove that there is just one curve corresponding to a point in∗W ⊂∗Σ which is tangent to Ctin the monad of[0,0,1].
The part of Ctcontaining[0,ta,1]is given by the equation


and any(x,y)∈Uεimplies there is a unique curve corresponding to w∈W with

as before.The above equality together with y=y gives a biholomorphic map ofto Uε,whereis a neighborhood of(0,0)in W×{y∈C||y|<ε}.Thus,can serve as a coordinate neighborhood of[0,0,1]in CP2,and in,a curve coming from Σ is represented by

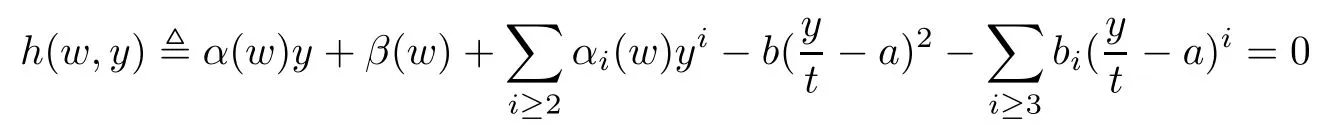
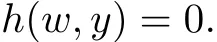
This equation gives w=w(y)for|−a|< ε as another representation of the relevant part of Ctin,and the curve w=w0∈∗W is a tangent line of it if and only if for some y0with|−a|< ε,w0=w(y0),and(y0)=0.
Now

and
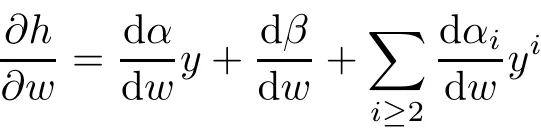
is a standard holomorphic function with

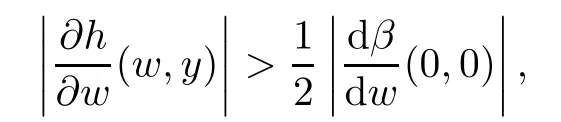
when(w,y)∈∗C2and|w|≤,|y|≤.Thus,for such(w,y),
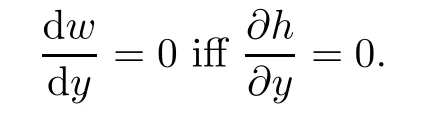
Since


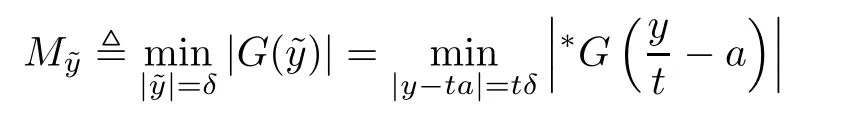
is a standard positive number.Also for sufficiently small δ>0,we have|w(y)|≤,for|y − ta| is in finitesimal.Thus,by Rouch´e theorem,G(− a)+tH(w(y),y)=0 has a unique solution y0of multiplicity one with|y0− ta| implies that(x0,y0)∈Ctmeans and w0=w(y0)is also an in finitesimal. To prove that w=w0is not a tangent line of higher order,we need to see(y0).From we get And we proved that there is a unique curve w=w0inwhich is tangent to Ctin the monad of[0,0,1]once.Thus,the n monads of the intersection points of the tangent lines of C from S with L contribute just nµ curves in the system∗Σ to tangent Ct. In this subsection,we need more strict choice for the line L.Since is a Zariski closed set in U of dimension less than or equal to 1,we can choose L further to let L=p2(u)for some u∈U−.Choose a coordinate system of CP2such that L is the x-axis,and[0,0,1]=p1(u)is the tangent point of L as the tangent line of the curve corresponding to p(u)∈˜Σ.Then for Uε,Uuand W as in Section 2.2,we have for the curves in Uεwith α(0)= β(0)=0,α2(0)6=0,and(0)6=0.Now in∗Uεfor ε small enough,Cthas m pieces,each has the form with the right side standard.As in Section 2.2 again with positions of x and y changed,a part of Ctis given inby the equation with w(x)solved by Now∗α(w(x))is an internal holomorphic function of x with|x|≤,and|∗α(w(x))|≤ some standard positive number,say M.For any such internal holomorphic function γ,by Chauchy formula whose correctness is guaranteed by the transfer principle,we have Hence Now w(0)satis fies i.e.,∗β(w(0))−=0,β(0)=0 and(0)6=0 imply β is an invertible function in a neighborhood of 0.Hence∗β(w(0))=t˜β implies w(0)being in finitesimal. Since we have Now must be in finitesimal,since α(0)=0 and w(0)being in finitesimal imply∗α(w(0))being infinitesimal.Thus,we have proved Let Then and Furthermore, for all sufficiently small δ>0.By using Rouch´e theorem again,we see that has a unique solution x0with|x0|< δ for all small standard δ,hence x0must be in finitesimal. To see w0=w(x0)being in finitesimal, first we have from that A previous estimate has already shown that And together with α2(0)6=0 and w(x0)being in finitesimal implies that the standard part of(x0)is a nonzero complex number. So far,we proved that for any given one of the m pieces of Ctin the monad of[0,0,1],and any given one of the ν points inwhose corresponding curves have L as a tangent line,there is a unique curve corresponding to a point in the monad inof the given point in˜Σ,which is tangent to the given piece of Ctin the monad of[0,0,1]once. To see the total contribution of the monads of the tangent points on L as a tangent line of the curves corresponding to the ν points inis mν,we must check all the curves in the system Σ which pass through[0,0,1].Recall that we have u∈U−,L=p2(u),[0,0,1]=p1(u).A curve in Σ passes through[0,0,1]i ffit is p(u˜)for some([0,0,1]).If([0,0,1])∩(L),its contribution has already been counted.If([0,0,1])−(L),the curve corresponding topasses through[0,0,1]with tangent line being not L.Thus,the curves in the monad ofin∗Σ all have tangent lines in the monad of[0,0,1]with standard parts being not L.While all the tangent lines of the parts of Ctin the monad of[0,0,1]have standard part L.Hence those˜u contribute nothing.The proof for the contribution mν is completed. For all points[x,0,1]other than those in Sections 2.2 and 2.3,and the point[1,0,0],all tangent lines at the points of Ctin their monads have standard part L.Let q be any one of above points on L. p2((q))is a Zariski closed set of CP2−{L},and∗p2((the monad of q in∗CP2))⊂∗CP2− the monad of L.Hence,the standard part of any tangent line of any curve in∗Σ with tangent point in the monad of q is not L.Thus,in the monad of q,Ctand all curves coming from∗Σ cannot tangent. From Sections 2.2–2.4,we see that there are exactly mν +nµ points in∗U whose images under p1are the tangent points of curves in∗Σ with Ct.While to see each of them has multiplicity one,we encounter a difficulty.That is they are in the variety∗U ⊂∗CPN×∗CP2×∗CP2,and Ct⊂∗CP2. To make multiplicity one or transversality meaningful,we need appeal to the fl ag variety F consisting of associated points and lines on CP2,i.e., Then,we see that The map p1×p2:U→p1×p2(U)is in general not one to one.But we have Theorem 2.2p1×p2:U→p1×p2(U)is a birational equivalence. ProofLet u∈U−be as in the beginning of Section 2.3.Assume that there is a u′∈U−˜U such that u′6=u,and p1×p2(u′)=p1×p2(u).Then we may choose coordinate neighborhoods Uε,andof u,u′and p1(u)respectively,such that Uε∩U=∅,and p1:Uε→and p2:are both biholomorphic.Let W,W′⊂C be coordinate neighborhoods of p(u)and p(u′)in Σ.We may assume also that p1(u)=p1(u′)=[0,0,1],{(w,x)|w ∈ W,|x|< ε}and{(w′,x)|w′∈ W′,|x|< ε}are also coordinate systems around u and u′,respectively. Then,by the biholomorphisms between Uε,and,we have a biholomorphism given by for some g,such that p1×p2(g(w,x),x)=p1×p2(w,x).Now a curve from Σ inis given by the equation w′=for a constant,and solving yields a curve w=w0(x)in Uεsuch that For any x0with|x0|<ε,denote w0(x0)by w0.Then is the equation of a curve from Σ in Uε.Thus,we have p2(,x0)is the tangent line of the curve p1({w′=})at p1(,x0),and p2(w0,x0)is the tangent line of the curve p1({w=w0})at p1(w0,x0).Hence p2(,x0)=p2(w0,x0)implies,by the commutative diagram that the curves w=w0(x)and w=w0are tangent at(w0,x0)∈ Uε.This means that Hence w′=g(w),and curves corresponding to w∈W and w′=g(w)∈W′are identical in.This shows that we must have Uε=,since Σ is irreducible.The proof for the theorem is completed. ? Let Ccbe the curve f?x,,z?=0 for c∈C−{0}.Then there is naturally a 1-dimensional system consisting of curves with degree m and with CP1=C∪{∞}as parameter space,where C0is given by ym=0,and C∞is given by f(x,0,z)=0.Also we have a 2-dimensional variety UC(if C is irreducible,so is UC)such that and p(UC)=CP1,p1×p2(UC)⊂F with p1×p2:UC→p1×p2(UC)being a birational equivalence,as for the case of Σ. Now for c,c′∈ CP1,p−1(c)and p−1(c′)are rationally equivalent cycles.Since p1× p2:UC→ F is a proper morphism,p1×p2(p−1(c))and p1×p2(p−1(c′))are also rationally equivalent cycles(c.f.[2]p.11).So∗p1×∗p2(∗p−1(c))and∗p1×∗p2(∗p−1(c′))for any c,c′∈∗CP1rationally equivalent by the transfer principle. Thus,for any c ∈∗CP1,∗p1×∗p2(∗p−1(c)),the number of its intersections with∗p1×∗p2(∗U)in∗F will be either ∞ or a common finite number.To see this common number is mν+nµ,we need to prove that for c=t with t being any in finitesimal,any of the mν+nµintersections obtained in Sections 2.2 and 2.3 has multiplicity one. To see this,we give first the equation of F in CP2×CP2by For the point[x1,x2,x3]× [y1,y2,y3]=[0,0,1]× [0,1,0]in F,the above equation in its affine neighborhood C2×C2⊂CP2×CP2becomes Thus,this affine part of F is the graph of the function Now in the case of Section 2.3,the curve for w∈W is given by Its tangent line at(x′,H(w,x′))is Regard this as a point[x1,x2,1]×[y1,1,y3]in F,we have where This gives a piece of a 2-dimensional subvariety in F.For a part of Ctin a standard neighborhood of[0,0,1]in∗C2,its equation is and its tangent line at the point[x′′,t∗G(x′′),1]is which gives a point in∗F by where This gives a piece of a 1-dimensional internal subvariety of∗F.We already saw in Section 2.3 that there is a unique(w0,x0)with w0and x0both in finitesimal,such that the nonstandard extension of the standard 2-dimensional one and the 1-dimensional one intersect in∗F with parameters(w,x′)=(w0,x0)and x′′=x0,respectively. Let Then We already proved in Section 2.3 that Hence, This shows that the intersection is transversal.The same conclusion is obtained similarly for the case in Section 2.2 by changing(x,y)to(y,x). So far,we proved that for any in finitesimal t 6=0,Cthas just nµ+mν different points at each of which it is tangent to a curve of∗Σ so that the contact is not of higher order.And it is also showed that the contacts are all transversal in∗F,i.e.,the multiplicities are all one. By the transfer principle,we see that there is a standard nonzero c∈C such that the curve Cchas exactly nµ+mν different points sharing the same as Ct.Such kind of c∈ C form a nonempty Zariski open set,and hence its complement is a finite set.For c in this finite set,Ccmay have in finite points contacting with curves in Σ,while otherwise,the contacting points are nµ+mν,if multiplicities are counted.








2.3 Contribution of the Tangent Points on L

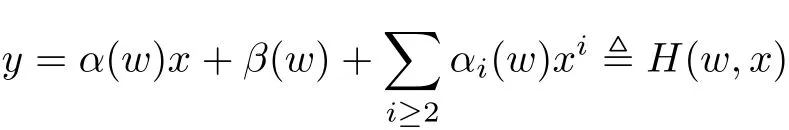


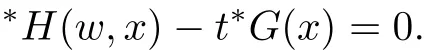



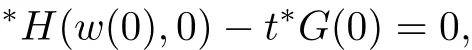
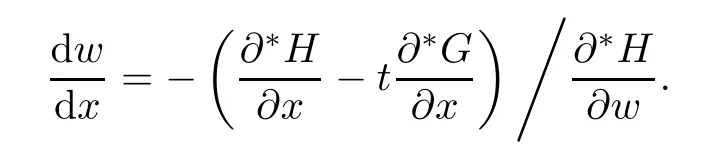

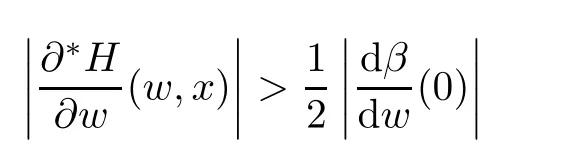
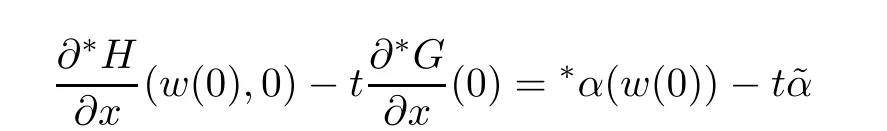

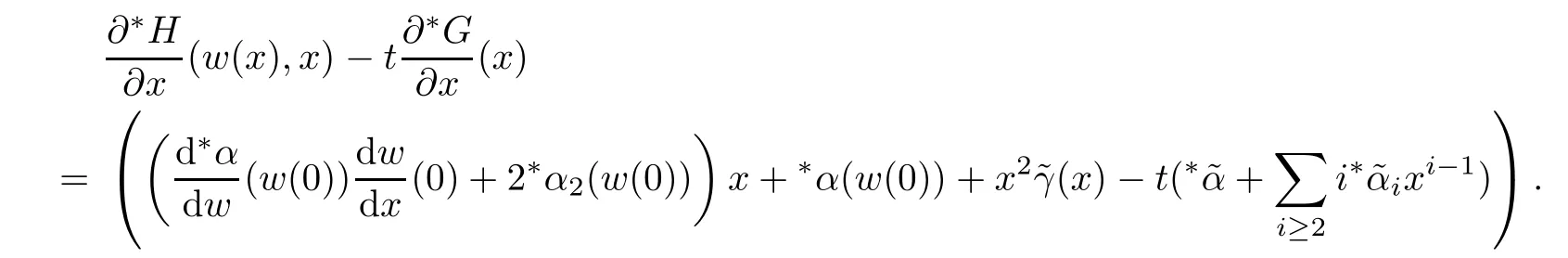
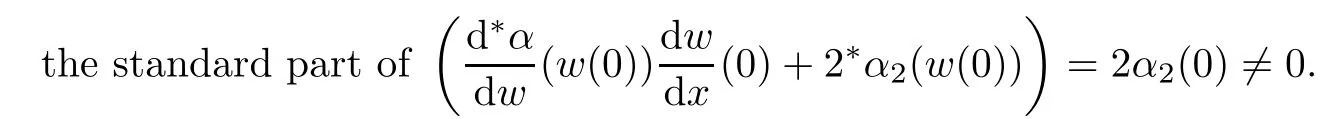
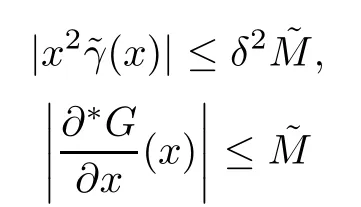
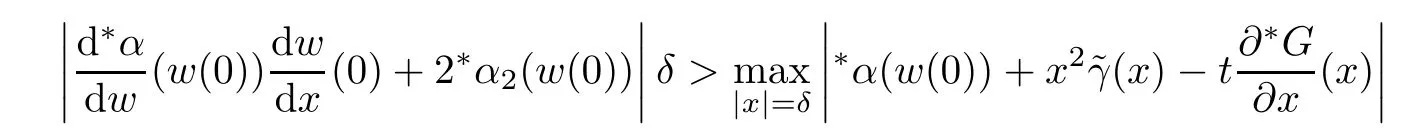


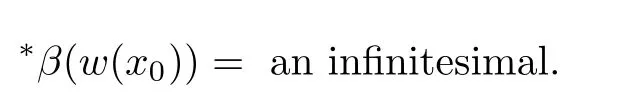
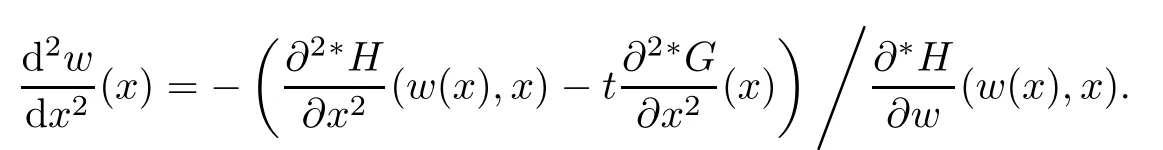

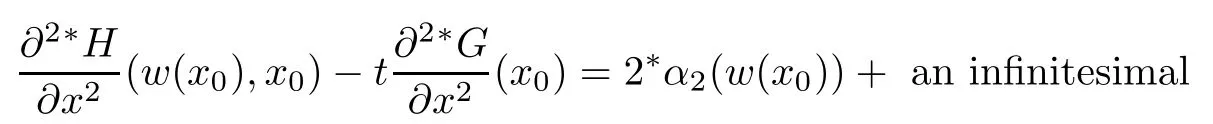
2.4 The Contribution of Other Points on L
2.5 Transversality



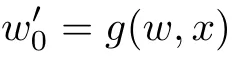





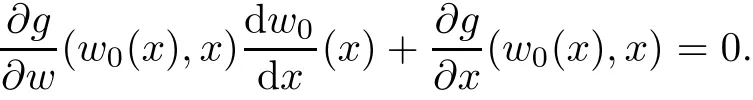
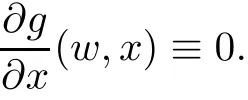

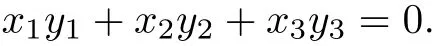

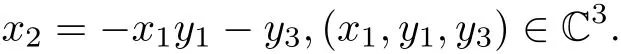


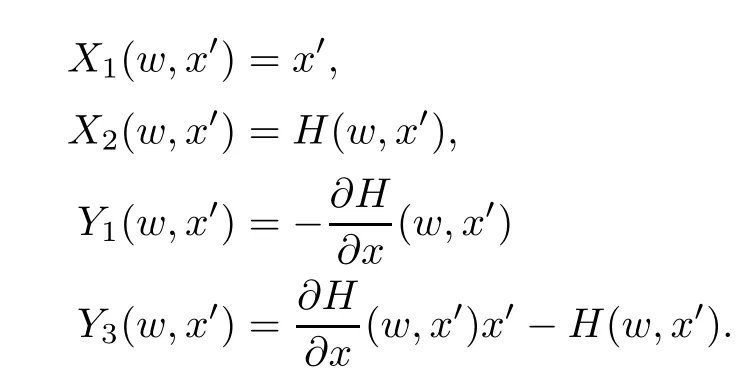



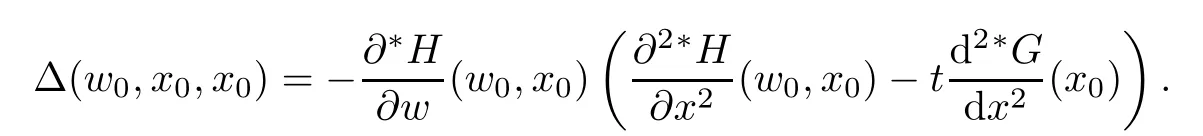

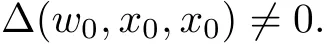
2.6 Conclusion
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- INFINITELY MANY SOLITARY WAVES DUE TO THE SECOND-HARMONIC GENERATION IN QUADRATIC MEDIA∗
- COMPLEX SYMMETRIC TOEPLITZ OPERATORS ON THE UNIT POLYDISK AND THE UNIT BALL∗
- THE BOUNDEDNESS FOR COMMUTATORS OF ANISOTROPIC CALDER´ON-ZYGMUND OPERATORS∗
- GROUND STATES FOR FRACTIONAL SCHR¨ODINGER EQUATIONS WITH ELECTROMAGNETIC FIELDS AND CRITICAL GROWTH∗
- MULTIPLE JEEPS PROBLEM WITH CONTAINER RESTRICTION∗
- THE EXISTENCE AND LOCAL UNIQUENESS OF MULTI-PEAK POSITIVE SOLUTIONS TO A CLASS OF KIRCHHOFF EQUATION∗
