凯威特单层球面网壳的几何缺陷相关性

刘 俊，罗永峰，张玉建

凯威特单层球面网壳的几何缺陷相关性

刘 俊，罗永峰，张玉建

(同济大学土木工程学院，上海 200092)

凯威特单层球面网壳结构的稳定性对初始几何缺陷非常敏感，特别是节点位置安装误差造成的结构曲面形状偏差．由于单层网壳结构各节点之间由刚性杆件连接，因而不同节点的位置偏差具有相关性．理论分析和实测数据均表明，单层球面网壳结构中节点距离越远，节点位置偏差的相关性越弱．根据对节点位置偏差相关系数的计算推导和分析，建立以节点空间距离为自变量的相关系数函数，提出初始几何缺陷相关性的分式函数计算模型，并给出具有相关性的初始几何缺陷生成方法．建立凯威特单层球面网壳结构数值模型，根据提出的分式函数模型生成具有相关性的初始几何缺陷，将缺陷引入模型并进行整体稳定性分析，结果表明缺陷相关性会对结构整体稳定承载力产生明显影响．进一步对缺陷相关性进行参数分析，将不同相关程度和不同规模大小的缺陷引入模型中并计算结构整体稳定性，结果表明：初始几何缺陷较小时，相关性总是有利于结构稳定性；而缺陷较大时，结构稳定承载力会随相关性增强先减小后增大，中等程度相关性会对结构稳定性产生不利影响．因此，忽略缺陷相关性可能会使凯威特单层球面网壳结构稳定承载力的计算结果偏于危险，取相关系数为0.5进行分析，能有效考虑不利的相关缺陷．

单层球面网壳；几何缺陷；相关性；整体稳定性

单层网壳结构具有薄壳结构的受力特征，其稳定性对初始几何缺陷非常敏感，特别是节点位置安装误差造成的结构曲面形状偏差[1-3]．节点位置误差在施工中具有随机性，因而分析结构整体稳定性时，初始几何缺陷可以采用多维随机变量表示，其样本空间的每个样本都对应着一种缺陷分布模式，即随机缺陷模态[4]．基于随机缺陷模态对单层网壳结构稳定性进行全概率分析，可以得到极限荷载的概率分布及其数值特征，并依此评估结构稳定承载力．考虑到计算成本，一致缺陷模态等实用型缺陷模态被提出并应用[5]，而随机缺陷模态由于较为真实地涵盖了结构实际缺陷分布模式，因此多用于评价各类实用性缺陷的准确性和可靠性[6-8]．

在单层网壳结构几何缺陷的研究过程中，节点位置偏差的相关性往往被忽略．网壳结构各节点由杆件相连接，位置会相互影响，因而位置偏差具有一定的相关性[9]．相关性是决定多维随机变量联合分布的一种重要因素，缺陷的相关性会改变缺陷分布模式，影响结构稳定承载力．然而，缺陷相关性目前尚未受到重视，对于相关性如何产生、是否会影响结构稳定性以及如何影响等问题，尚无深入研究．随机缺陷模态法作为各类实用型缺陷评价标准，其自身的准确性是各类研究的基础，忽略相关性可能会使分析结果不可靠；而对于实用方法，考虑相关性有助于得到更有效的实用型缺陷模态，因此，有必要对单层网壳结构几何缺陷的相关性进行深入研究．

本文对工程中广泛应用的凯威特单层球面网壳进行研究，分析节点位置偏差的相关性产生原理及其特征，推导出缺陷相关性的理论模型，并基于考虑相关性的随机缺陷模态法，对凯威特单层球面网壳结构稳定性进行数值算例分析，研究相关性对稳定承载力的影响规律．

1 网壳结构的缺陷相关性

1.1 相关性分析

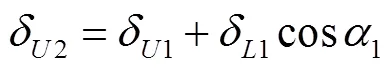
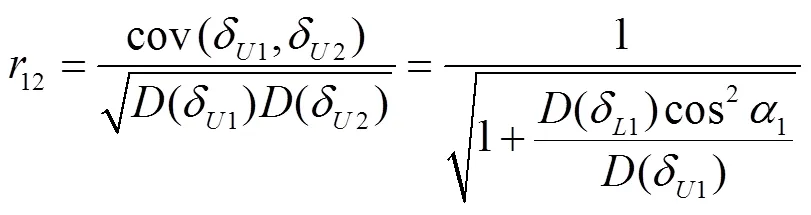
式中：D(δU1)和D(δU2)分别表示δU1和δU2的方差；cov(δU1，δU2)表示δU1和δU2的协方差；D(δL1)表示δL1的方差．

分析式(1)可知，(δ1)越小，12越大，即δ1和δ2相关性越强；(δ1)取0时，12为1，即δ1和δ2完全线性相关．由此可见，节点之间的连接杆件使得其位置偏差存在相关性，并且，杆件制造精度越高，偏差相关性越强．

同样，根据结构几何关系，忽略杆件角度偏差，可以计算得到δ1和δ3的相关系数13为

式中(δ2)表示δ2的方差．对比式(1)和(2)可以发现，δ2的存在使得13小于12．这表明节点连接路径上杆件数量越多，偏差的相关性越弱．

文献[9]和[10]在单层网壳结构节点位置偏差的实际测量数据分析中，均发现偏差存在相关性，且相关性随节点距离增大而减弱．由此可见，实测数据同样表明单层网壳结构节点位置偏差存在一定相关性，且节点距离越大，相关性越弱．

1.2 相关性模型

实际网壳结构节点位置偏差的相关性受到多种因素影响，包括杆件角度偏差、节点尺寸偏差和螺栓或焊缝尺寸偏差等，这些因素往往是未知的，导致实际结构中相关性难以直接进行理论推算．由于同一网壳结构中各杆件长度较为接近，不同位置处的杆件长度等尺寸精度一般处于同一水平，因而，空间距离相同的节点理论上具有较为接近的相关性．将节点位置偏差的相关系数假定为以节点距离为自变量的函数，可以有效计算偏差的相关性．

在空间相关性分析理论中[11]，常用的相关系数函数主要为指数函数型和幂函数型，现有研究也均基于此类函数对网壳结构的缺陷相关性进行分析，尚未有研究从理论上推导相关系数函数模型．本文根据推导得到的相关系数计算式(1)和(2)，提出缺陷相关性的分式函数模型，即

式中：为相关系数；为节点空间距离；为待定系数，由结构杆件制造精度等因素决定．

对于凯威特单层球面网壳，根据其几何特征，结构杆件长度较为均匀，因此，节点距离与节点最短连接路径上的杆件数量近似呈正比．为简化计算，自变量可采用连接杆件数量等效代替[9]，即

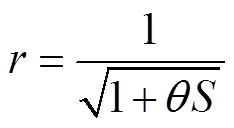
式中为节点最短连接路径上的杆件数量．

基于上述函数模型，可通过以下步骤计算具有相关性的节点位置偏差．

(1) 结构中任意第个和第个节点最短连接路径上的杆件数量记为S，将其代入式(4)可计算得到相关系数r．

(2) 将r置于矩阵的第行第列，记网壳的节点总数为，则全部节点的相关系数可组成一个×的对称正定矩阵，记为相关系数矩阵．

(3) 对进行Cholesky分解，即

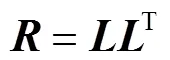
式中：为下三角矩阵；T为的转置矩阵．

(4) 对于服从某一概率分布的初始几何缺陷，采用蒙特卡洛法模拟生成一组节点位置偏差，记为向量．将与相乘可以得到新的向量，即

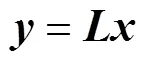
此时，向量即是服从此概率分布且具有相关性的一组节点位置偏差．采用蒙特卡洛法模拟生成多组节点位置偏差，由式(6)便可计算得到多组相关缺陷．

1.3 相关缺陷

根据概率论和数理统计理论，相关性不会对单个随机变量的概率分布产生影响，但是会改变变量的联合概率分布．以2个正态分布随机变量为例，其边缘分布均为相同的标准正态分布(单个变量的分布不变)，相关系数取0和0.5时，联合分布如图2所示．可以看出，考虑相关性使得随机变量的联合分布发生了明显变化．这表明，采用多维随机变量模拟单层网壳结构初始几何缺陷时，未合理考虑偏差间的相关性，可能会使随机缺陷模态无法真实模拟实际缺陷的分布模式．

若结构初始几何缺陷具有相关性，则距离近的节点易产生较为接近的偏差，此时，结构整体几何形状更加平滑．若采用不相关缺陷分析单层球面网壳结构整体稳定性，多数情况下会使结果偏于保守，因为单层球面网壳结构的整体失稳表现为平面外变形过大，不平滑的缺陷模态容易引起结构局部受力变形过大，造成失稳并传播，最终导致结构整体失稳．但是，某些情况下，平滑的缺陷模态更容易直接导致结构较大区域失稳，此时，不考虑缺陷相关性会偏于危险.为此，本文将采用数值算例研究相关性对结构稳定承载力的影响．

2 算例分析

2.1 结构模型

本节基于节点位置偏差的相关系数函数，分析具有相关缺陷的单层网壳结构的稳定性，算例模型采用K6型凯威特单层球面网壳，跨度为50m，矢跨比为1/5，环数为9．结构由702根杆件和271个节点组成，杆件截面尺寸如图3所示，材料为Q235钢材．采用Ansys软件建立有限元模型，杆件均采用Beam188单元，节点均为刚接节点，支座均为刚接固定支座．材料采用理想弹塑性模型，弹性模量为206GPa，泊松比为0.3，屈服强度为235MPa．荷载采用均布恒载D＝0.4kN/m2和均布活载L＝0.75kN/m2，荷载组合为1.0D＋1.0L．

2.2 整体稳定性分析

对完善结构进行整体稳定性分析，得到结构线性屈曲的最低荷载因子为11.988．考虑几何非线性，对结构进行弹性和弹塑性荷载-位移全过程分析，得到极限荷载因子(记为)分别为9.520和5.657．

分析缺陷结构整体稳定性时，初始几何缺陷采用随机缺陷，不考虑缺陷相关性，节点各方向上的位置偏差均采用均值为零、标准差为50mm的正态分布变量[4]．由蒙特卡洛法模拟生成1000组初始几何缺陷样本，典型缺陷如图4(a)所示．将缺陷样本分别引入结构模型中并进行弹性和弹塑性稳定分析，得到的极限荷载因子的分布如图5所示，其均值(记为a)分别为4.283和2.665，99.7%分位值(记为q，3倍标准差原则[8])分别为3.315和2.124．

以极限荷载因子分布的分位值q作为缺陷结构稳定承载力评价指标，将计算结果列于表1，对比完善结构，缺陷结构稳定性降低超过50%，由此可见凯威特单层球面网壳结构具有很高的缺陷敏感性．

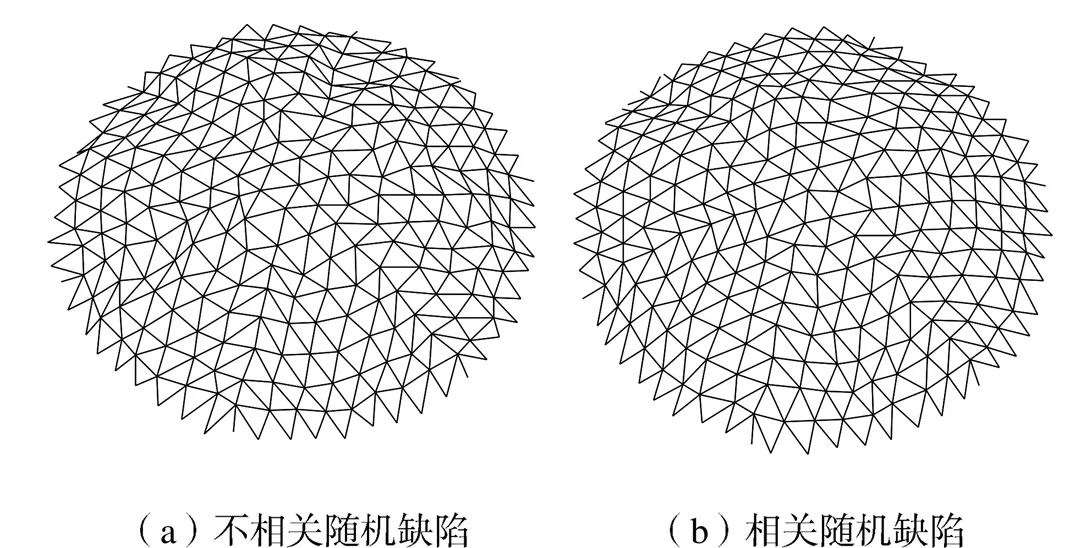
图4 初始几何缺陷

图5 极限荷载因子分布

表1 极限荷载因子

Tab.1 Ultimate load factors

考虑节点位置偏差的相关性，相关系数采用本文提出的式(4)计算，其中取为1.78，使得等于1时等于0.6，即直接相连节点间的相关系数为0.6．基于式(4)计算得到的相关系数，生成1000组相关缺陷样本，典型缺陷如图4(b)所示．相关缺陷结构分析结果同样绘于图5中，弹性和弹塑性极限荷载因子均值a分别为4.527和3.035，分位值q分别为3.314和2.427．对比可以发现，缺陷相关性对结构稳定性有明显影响，弹性和弹塑性稳定均值分别提高5.7%和13.9%；弹性稳定分位值相近，但是弹塑性稳定分位值相差达到14.2%．

极限荷载因子的均值a和分位值q随缺陷样本数量的变化关系如图6所示，缺陷样本数量达到200时，计算结果均已基本稳定．由此可见，相关缺陷和不相关缺陷对样本量的需求无明显差异，结构分析得到的稳定承载力存在明显差异，因此，缺陷相关性会对稳定承载力产生影响．

图6 极限荷载因子与样本数量散点图

3 相关性对结构稳定的影响规律

3.1 相关程度

相关程度是指相关性的强弱．根据前文分析，结构杆件尺寸精度越高，节点位置偏差相关性越强．相应地，分式函数模型式(3)或(4)中参数值也越小．对于不同结构，由于制造安装精度不同，其缺陷相关程度也随之变化．本文采用结构的最大相关系数表示缺陷相关程度，记为m，m即为距离最近的节点的相关系数．在式(4)的分式函数模型中，m即为＝1时的值．确定m值后，将其代入式(4)计算参数值，便可得到该相关程度对应的相关系数函数．

本节m分别取0.1，0.2，…，0.9，代表由弱至强9种程度的相关性[12]，将m代入式(4)，得到对应于9种相关程度的相关系数函数．基于各相关系数函数，对第2.1节模型采用随机缺陷模态法计算结构弹性和弹塑性稳定，得到极限荷载因子分布．将a和q随m的变化关系绘于图7中，图中m为0对应无相关性缺陷时的分析结果．

图7 相关程度分析结果

由图7可知，随m增大，弹性稳定分析得到的q先减小再增大，m为0.4时达到最小，相较于m为0时q降低约6.8%；弹塑性稳定分析得到的q先呈水平变化趋势，再逐渐增大．m为0.9时，弹性和弹塑性稳定的q分别增大52.5%和59.1%．由此可见，缺陷的相关程度不同，结构稳定承载力也随之发生明显变化．特别是在弹性稳定分析中，考虑缺陷相关性时出现了稳定承载力下降现象．这表明，仅考虑不相关缺陷并非总是保守的，也可能会使分析结果偏于危险.

3.2 缺陷大小

本节基于缺陷相关程度分析，对不同缺陷大小的情况进行研究．节点位置偏差的分布类型仍采用正态分布，以标准差表征缺陷大小，记为s．s与m的参数方案组合如图8所示，对于每种参数组合，均进行随机缺陷模态法分析，得到结构弹性和弹塑性稳定极限荷载因子的分布，并计算其99.7%分位值q．以m为0时的q值为基准，计算q的增量百分比q，q随m变化关系如图9所示．

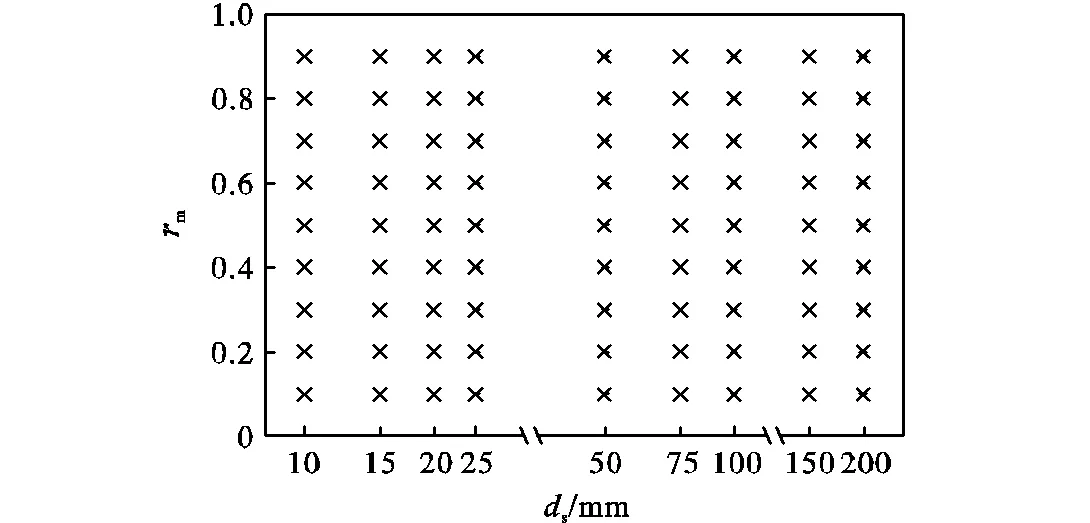
图8 参数方案

图9 参数分析结果

由图9可知，不同缺陷大小情况下，相关性均会对稳定承载力产生影响，但q随m的变化趋势不同．当s小于50mm时，q几乎随m增大单调增加；当s大于50mm时，q随m增大先减小后增加，存在明显的极小值点．由此可见，在缺陷规模较小时，相关性总是会对结构整体稳定有利，但是缺陷规模较大时，存在对稳定性不利的情况．

统计学理论中通常以相关系数为0.3和0.7为界，将相关性分为弱相关性、中等相关性和强相关性3类．可以看出，当缺陷相关性对结构整体稳定性不利时，其最不利的情况出现于中等相关性．而中等相关程度的缺陷在实际工程中最为常见，文献[9]和[10]中实际偏差测量数据的相关性均为中等相关性，因此，对网壳进行稳定性分析，应合理考虑中等程度的相关性．

将图9中的最不利分析结果列于表2，同时还将m为0.5的结果列于表中．对比可知，当相关性明显降低结构稳定性时，m为0.5时的分析结果与最不利结果相差均小于5%，因此，本文建议对m为0.5的相关缺陷进行分析，以充分考虑不利的相关性．

表2 参数分析结果统计

Tab.2 Statistics of the parametric analysis

4 结 论

单层球面网壳结构的节点位置偏差具有相关性，本文通过对相关系数进行计算推导和理论分析，提出了缺陷相关性的分式函数计算模型．基于此模型，本文通过算例分析得出以下结论：

(1) 相关性会对凯威特单层球面网壳结构整体稳定承载力产生明显影响；

(2) 缺陷较小时，相关性总是有利于结构稳定性；缺陷较大时，稳定承载力随相关性增强先减小 后增大，中等程度相关性会对结构稳定性产生不利 影响；

(3) 忽略缺陷相关性可能会使结构稳定承载力计算结果偏于危险，取相关系数为0.5进行分析，能充分考虑不利的相关缺陷．

［1］ Bulenda T，Knippers J. Stability of grid shells[J]. Computers & Structures，2001，79(12)：1161-1174.

［2］ 罗永峰，刘 俊. 既有空间结构位形推算的随机偏差方法[J]. 同济大学学报：自然科学版，2017，45(6)：791-798，813.

Luo Yongfeng，Liu Jun. Stochastic deviation method of reckoning geometric shapes of existing spatial structures[J]. Journal of Tongji University：Natural Science，2017，45(6)：791-798，813(in Chinese).

［3］ 刘 俊，罗永峰，杨旭. 基于曲面插值的既有网壳结构节点位置推算方法[J]. 上海交通大学学报，2018，52(11)：1475-1482.

Liu Jun，Luo Yongfeng，Yang Xu. A method of reckoning nodal positions of existing grid shell structures based on surface interpolation[J]. Journal of Shanghai Jiao Tong University，2018，52(11)：1475-1482(in Chinese).

［4］ 沈世钊，陈 昕. 网壳结构稳定性[M]. 北京：科学出版社，1999：52-56.

Shen Shizhao，Chen Xin. Stability of Single-Layer Reticulated Shells[M]. Beijing：Science Press，1999：52-56(in Chinese).

［5］ Liu H，Wei Z，Hao Y. Structural stability analysis of single-layer reticulated shells with stochastic imperfections[J]. Engineering Structures，2016，124：473-479.

［6］ Fan F，Cao Z，Shen S. Elasto-plastic stability of single-layer reticulated shells[J]. Thin-Walled Structures，2010，48(10/11)：827-836.

［7］ 蔡 健，贺 盛，姜正荣，等. 单层网壳结构稳定分析中初始几何缺陷最大值的研究[J]. 建筑结构学报，2015，36(6)：86-92.

Cai Jian，He Sheng，Jiang Zhengrong，et al. Investigation on maximum value of initial geometric imperfection in stability analysis of single layer reticulated shells[J]. Journal of Building Structures，2015，36(6)：86-92(in Chinese).

［8］ He S，Jiang Z，Cai J. Investigation on simulation methods of initial geometric imperfection distribution in elasto-plastic stability analysis of single-layer reticulated shells[J]. KSCE Journal of Civil Engineering，2018，22(4)：1-10.

［9］ Chen G，Zhang H，Rasmussen K J R，et al. Modeling geometric imperfections for reticulated shell structures using random field theory[J]. Engineering Structures，2016，126：481-489.

［10］ 刘 俊，罗永峰，杨 旭，等. 基于节点位置相关性分析的结构位形推算方法[J]. 湖南大学学报：自然科学版，2019，46(3)：74-81.

Liu Jun，Luo Yongfeng，Yang Xu，et al. A new approach to calculating structural geometric shape based on the correlation analysis of nodal positions[J]. Journal of Hunan University：Natural Sciences，2019，46(3)：74-81(in Chinese).

［11］ Onyejekwe S，Kang X，Ge L. Evaluation of the scale of fluctuation of geotechnical parameters by autocorrelation function and semivariogram function[J]. Engineering Geology，2016，214：43-49.

［12］ Taylor R. Interpretation of the correlation coefficient：A basic review[J]. Journal of Diagnostic Medical Sonography，1990，6(1)：35-39.

Correlation of the Geometric Imperfection of Kiewit Single-Layer Latticed Spherical Shell

Liu Jun，Luo Yongfeng，Zhang Yujian

(School of Civil Engineering，Tongji University，Shanghai 200092，China)

The global stability of Kiewit single-layer latticed spherical shells is sensitive to initial geometric imperfection，particularly the imperfection of surface shapes caused by the positional deviations of structural nodes．Given that the nodes in a latticed spherical shell are connected by rigid rods，their positional deviations are correlated．From the theoretical analysis and practical data，the correlation coefficient of the positional deviations of the nodes decreases with the increase in nodal distance in the structure．To compute the correlation coefficient，a fractional function model that uses nodal distance as the independent variable was proposed．The steps used to derive the correlated positional deviations of the nodes were also given．On the basis of the fractional function model，a case study of a Kiewit single-layer latticed spherical shell was performed，which indicated that the correlation significantly influences the structural stability．The influence was assessed by further parametric analysis of the degree of correlation and the magnitude of geometric imperfection．Results showed that，when the magnitude of geometric imperfection is small，any degree of correlation enhances the structural stability．By contrast，when the magnitude of geometric imperfection is large，the structural collapse load initially decreases and subsequently increases with the increase in the degree of correlation．In other words，a medium degree of correlation reduces the structural stability．In conclusion，overlooking the degree of correlation might lead to an incorrect assessment of structural stability．And，a medium degree of correlation with the correlation coefficient equal to 0.5 was proposed．

single-layer latticed spherical shell；geometric imperfection；correlation；global stability

Supported by the National Natural Science Foundation of China(No.51678431).

TU393

A

0493-2137(2020)05-0535-07

10.11784/tdxbz201906023

2019-06-12；

2019-09-09.

刘 俊（1993—  ），男，博士研究生，Jun_L@tongji.edu.cn.

罗永峰，yfluo93@tongji.edu.cn.

国家自然科学基金资助项目(51678431).

(责任编辑：刘文革，樊素英)