基于影响因素筛选-优化组合模型的隧道变形预测研究
2020-04-25薛晓辉
薛晓辉
(陕西铁路工程职业技术学院,陕西 渭南 714000)
受地质条件、施工条件等因素的综合影响,隧道监测数据往往具有非线性特性,且随机性较强[1-3]。基于上述特点,隧道变形受多种因素影响,若要开展隧道变形研究,需先分析隧道变形影响因素[4-5]。目前,在隧道变形影响因素研究方面,许多学者均已开展了相应的研究,如王智超等[6]基于室内试验参数构建了隧道三维数值模型,得到不同影响因素对隧道变形的时变特征;郭兵兵等[7]以正交试验为设计基础,利用三维模型分析了若干典型因素对隧道变形的影响程度,为隧道设计提供了参考依据;尹静等[8]构建了滑坡区隧道变形影响因素分析的本构模型,掌握了该类灾害区隧道变形的主要影响因素。在隧道变形预测方面,也有相关学者进行了研究,如强跃等[9]利用优化多步预测模型实现了隧道变形预测,并与传统预测结果对比,得出该模型具较高的预测精度及实用性;胡达等[10]、邱小梦等[11]构建了隧道变形的优化预测模型,并通过对比实测值与预测值间的相对关系,得出预测模型具较高的可靠性。上述研究虽取得了一定成果,但均未涉及变形影响因素分析与变形预测的综合研究,且在预测方法中,也未探讨RBF神经网络(径向基神经网络,Radical Basis Function Neural Network,简称RBF神经网络)的适用性。因此,研究以相关系数法及RBP神经网络为基础,构建了隧道影响因素筛选-优化组合模型,以期实现隧道变形的高精度预测,为隧道变形分析提供一种新的思路。
1 基本原理
研究过程为:以相关系数法为理论基础,通过相关系数来评价不同影响因素对隧道变形的影响程度,并确定出后期隧道变形预测模型的输入层参数;其次,以RBF神经网络为基础,构建隧道变形预测模型,并利用试算法及粒子群算法优化模型参数,以期实现隧道变形的高精度预测,以便为隧道安全施工提供参考依据。
1.1 相关系数法
相关系数法是基于统计学理论构建起来的一种分析方法,可以很好地评价相关指标间的紧密程度。若两评价对象表示为(xi,yi),i=1,2,…,n,则二者相关系数的计算公式为
(1)
其中:xi、yi为两评价对象中的第i个值;x′、y′为两评价对象的平均值。
相关系数值r可判断两评价对象间的相关性,判据为:当r>0时,说明两评价对象呈正相关,即两评价对象间的变化关系一致;反之,两评价对象呈负相关,即两评价对象间的变化关系相反;若r=0,说明两评价对象间无相关性。同时,r值的绝对值大小可判断两评价对象间的相关性程度,具体划分标准如表1所列。

表1 相关性程度划分标准
1.2 RBF神经网络
RBF神经网络是常用的神经网络方法之一,具有很强的自学能力,适用于非线性预测,进而将其作为隧道变形预测模型是可行的[12]。在RBF神经网络的应用过程中,其核函数类型一般为高斯函数,即
(2)
其中:R为核函数;σ为核函数宽度;xp为第p个输入样本;ci为核函数中心。
通过三维空间映射,即可实现RBF神经网络预测,其预测表达式为
(3)
其中:yi为第i个节点的输出值;h为隐层节点数;wij为隐层与输出层间的连接权值。
根据上述可知,隐层节点数、核函数中心c及核函数宽度σ对预测结果也具有较大影响,受使用者的经验影响较大,进而,为保证模型参数的准确性,该文对上述各参数进行优化处理,并将优化过程划分为两阶段:一阶段优化和二阶段优化,其中一阶段优化是利用试算法优化隐层节点数,二阶段优化是利用粒子群算法优化参数c和σ。
(1) 一阶段优化。隐层节点数的多少对RBF神经网络的预测效果具有较大影响,在传统神经网络的隐层节点数确定过程中,多是采用经验公式确定,即
(4)
其中:m为输入层节点数;n为输出层节点数;a为调节常数,取值范围为0~10。
将隐层节点数的优化过程分述如下:基于RBF的网络结构,先利用上述经验公式初步确定隐层节点数,再以该节点数为中心,上下扩展3个节点数范围,进而得到7个节点数;最后利用神经网络对上述确定的7个节点数进行逐一试算,得到预测效果最佳者即为最优隐层节点数。
(2) 二阶段优化。粒子群算法具较好的全局优化能力,进而将其用于RBF神经网络的参数优化过程是可行的。若粒子群的规模具有k个,则第i个粒子的位置为Xi、速度为Vi、个体极值为Pi,i=1,2,…,k。通过各粒子的迭代搜寻,得到所有粒子的全局极值为Pg,g=1,2,…,k,对比Pg中的所有值,效果最佳者即为最优粒子,其对应的属性参数即为最优参数。
粒子群算法的寻优过程中主要包括粒子迭代和优化程度评价,且粒子迭代主要是对粒子所处的位置及速度进行改变。
其中,速度迭代公式为
Vi+1=wVi+c1r1(Pi-Xi)+c2r2(Pgd-Xid),
(5)
速度迭代公式为
Xi+1=Xi+Vi+1,
(6)
其中:w为惯性向量;c1、c2为加速因子;r1、r2为加速因子;Pgd为对应粒子的全局极值;Xgd为对应粒子的位置极值。
同时,为评价迭代过程中各粒子的优化程度,利用适应度值进行评价,该值的计算公式为
(7)
其中:fk为第k个节点的适应度值;yk为第k个节点处的实测值;y′k为第k个节点处的预测值。
2 实例分析
2.1 数据来源说明
随着隧道所处深埋软岩环境的日益增加,其对应发生的工程问题也逐渐增多;同时,工程实践说明,该类隧道在开挖完成后,隧道变形常会持续增加,进而改变隧道所处的应力状态,造成隧道变形具蠕变特性。因此,深埋软岩隧道的变化状态具不确定性,使得开展深埋软岩隧道的变形研究具有较强的必要性。研究中的分析数据来源于文献[13],共计统计了隧道变形的13个影响因素及2个变形监测项目,其中变形监测量分别为拱顶沉降和水平收敛,相关统计数据如表2所列。
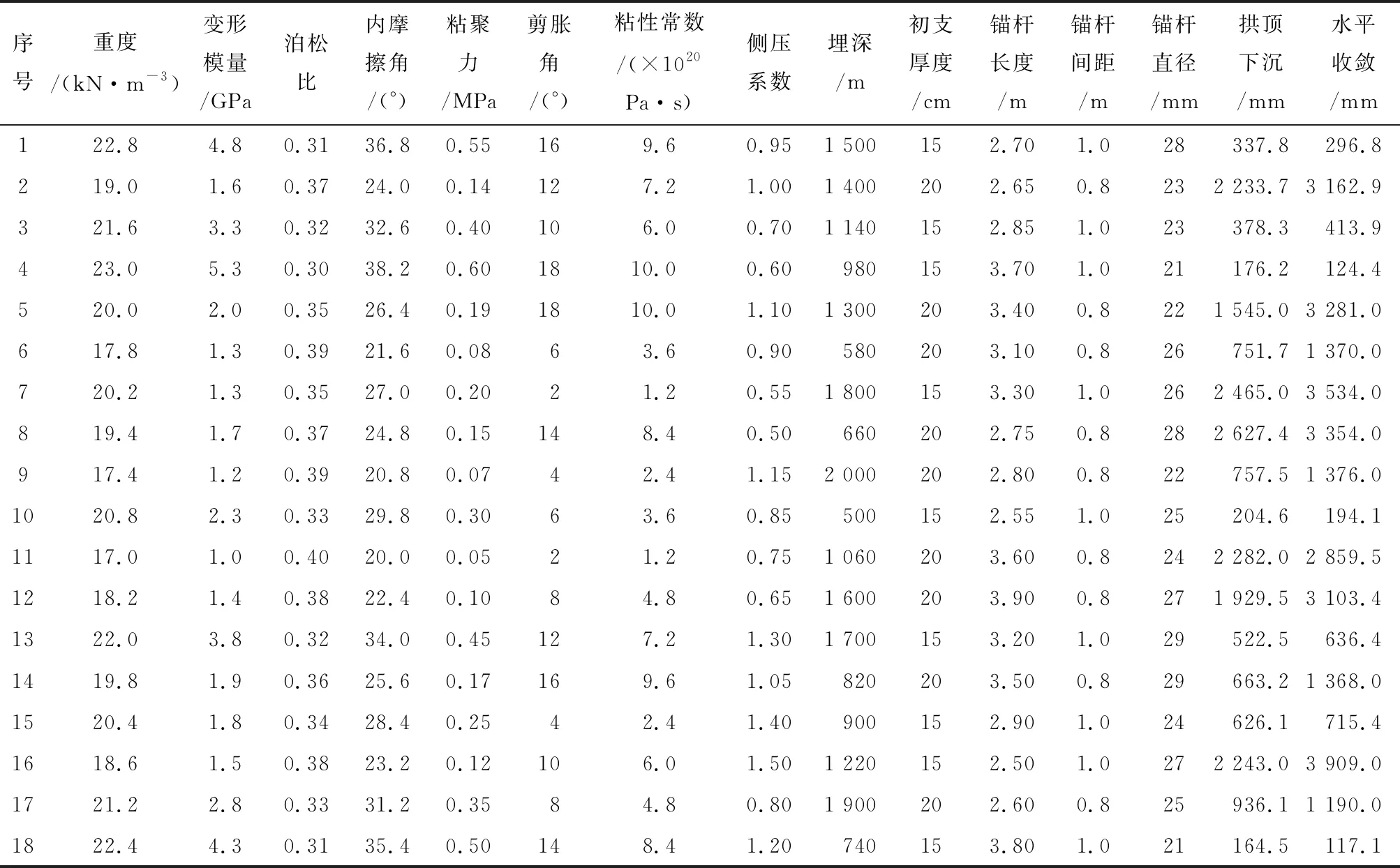
表2 深埋软岩隧道的变形影响因素统计
2.2 变形影响因素分析
由表2统计结果得出隧道变形影响因素较多,但不同因素对隧道变形的影响程度具一定差异,进而有必要探讨各因素的影响程度。在研究过程中,利用相关系数法来评价各影响因素与隧道变形间的相关性,且通过计算,得到各因素与拱顶沉降间的相关性参数,如表3所列。
据表3可知,各影响因素的相关性系数存在明显差异,验证了各因素对隧道变形影响程度的不同;同时,在相关性判断中,多数指标与拱顶沉降呈负相关,共计9个因素,占总因素的69.23%,反之,呈正相关的因素相对较少;另外,各影响因素的相关程度以中、低度为主,其中变形模量的影响程度相对最大,锚杆长度的影响程度相对最小。

表3 拱顶沉降与影响因素间的相关性统计
类比拱顶沉降的分析过程,对水平收敛与各影响因素间的相关性指标进行统计,如表4所列。由表4可知,各影响因素与水平收敛间的相关系数也存在较大不同,再次验证了分析各因素影响程度的必要性;各因素的相关性也多呈负相关,且负相关因素共计有9个,与拱顶沉降的负相关因素相同;最后,在各因素的相关程度评价过程中,有3个因素呈高度相关,相较于拱顶沉降因素,相关程度有了一定的提高,且变形模量的相关程度相对最高。

表4 水平收敛与影响因素间的相关性统计
综上所述,由于两类监测项目的主要影响因素存在明显差异,结合两者分析结果,确定以Ⅱ级以上相关因素作为对应监测项目的输入层指标,因此,在后期预测过程中,确定拱顶沉降的输入层为重度、变形模量、泊松比、内摩擦角、粘聚力、剪胀角、粘性常数、测压系数、初支厚度、锚杆长度及直径,共计11个指标,而水平收敛的输入层为重度、变形模量、泊松比、内摩擦角、粘聚力、埋深、初支厚度及锚杆间距,共计8个指标。
2.3 变形预测分析
鉴于有2个监测项目,为实现分析过程的合理性,以拱顶沉降的预测过程为初步验证,将水平收敛的预测过程作为预测模型可靠性验证。同时,在预测过程中,以1~13号样本作为训练样本,14~18号样本作为验证样本。
(1) 初步验证 结合RBF神经网络的优化思路,需先对隐层节点数进行筛选,基于前述相关系数分析结果,已确定拱顶沉降的输入层信息,且结合隐层节点数的经验公式,对RBF神经网络的初步隐层节点数进行求解。值得指出的是,为保证预测精度,将调节常数确定为10,进而确定拱顶沉降的初步节点数为14,隐层节点数的试算区间为11~17,且通过逐点试算,得到各隐层节点的预测结果,如表5所列。

表5 拱顶沉降预测过程的隐层节点试算结果
对比不同隐层节点数的试算结果可知,隐层节点数对RBF神经网络的预测效果具有较大影响,验证了优化隐层节点数的必要性,且隐层节点数并非越大越好,存在最优隐层节点数;同时,隐层节点数为15时预测效果相对最优,将其作为拱顶沉降预测过程中的隐层节点数。
利用粒子群算法优化参数c和σ,结果如表6所列。在相应验证样本处,对比粒子群算法优化前后的预测结果可知,通过粒子群算法的参数优化,相对误差值均出现了不同程度的减小,说明该方法合理实现了参数优化,达到了提高预测精度的目的;同时,优化后预测结果的相对误差均小于2%,平均相对误差仅为1.5%,说明该预测模型具较高的预测精度。
(2) 可靠性验证 类比拱顶沉降的预测过程,再对水平收敛进行预测,以验证该预测模型的可靠性,且通过计算,得到拱顶沉降的初步节点数为13,隐层节点数的试算区间为10~16,试算结果如表7所列。对比不同隐层节点数条件下的预测结果可知,隐层节点数的多少对预测效果具有较大影响,再次验证了隐层节点数优化的必要性,当隐层节点数为15时,预测效果相对最好,因此,在水平收敛预测过程中,确定其隐层节点数为15。
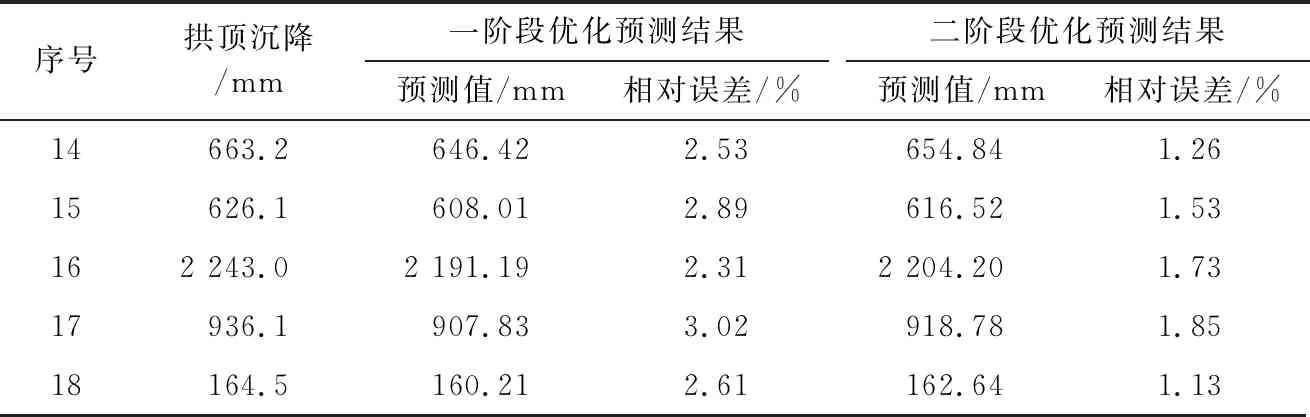
表6 拱顶沉降预测结果

表7 水平收敛预测过程的隐层节点试算结果
同理,利用粒子群算法优化参数c和σ,结果如表8所列。由表8可知,通过参数优化,水平收敛的预测精度也得到了相应的提高,且平均相对误差为1.47%,具有较高的预测精度,再次验证了该预测模型不仅具有较高的预测精度,还具有较高的可靠性。

表8 水平收敛预测结果
3 结论
通过相关系数法及优化RBF神经网络在隧道变形预测中的应用,得出如下结论:
(1) 相关系数法可以很好地评价各影响因素与隧道变形间的相关性程度,且不同监测项目的影响因素存在差异,其中,拱顶沉降与影响因素间的相关等级在Ⅱ级以上的指标共计有11个,而水平收敛与影响因素间的相关等级在Ⅱ级以上的指标仅有8个。
(2) RBF神经网络在隧道变形预测中具有较好的适用性,但传统模型在参数确定过程中的经验性要求较高,进而预测过程中的参数优化是很有必要的。同时,试算法和粒子群算法可以很好地优化隐层节点数及相关模型参数,能不同程度上提高预测精度。
(3) 该预测模型具有较高的预测精度,且可靠性高,验证了该方法在隧道变形预测中的适用性,但鉴于隧道所处地质条件、施工条件等因素的差异,建议在推广应用过程中,应对影响因素进行重新筛选,并重新优化相应参数,以保证预测效果。
