基于优化极限学习机的工业控制系统入侵检测

赵国新，陈志炼,2，魏战红+，刘 昱，宋非凡，郭家伟

(1.北京石油化工学院 信息工程学院，北京 102617；2.北京化工大学 信息科学与技术学院， 北京 100029；3.航天光华电子技术有限公司，北京 100070；4.福瑞博达(北京) 自动化设备有限公司，北京 100176)

0 引 言

近年来，工业控制系统(industry control system，ICS)[1]的信息安全问题越来越严峻，而入侵检测对网络入侵能进行主动防御，是一种有效的防护手段，因此，用于ICS的入侵检测成为了信息安全研究的一个方向[2]。在文献[3]中，把入侵检测看作为一个分类过程，就是将异常数据和正常数据进行分类[3]，常用的分类算法有决策树、神经网络、贝叶斯、支持向量机(support vector machine，SVM)等。极限学习机(extreme learning machine，ELM)[4]是黄广斌教授根据广义逆矩阵理论提出的新型的单隐层前馈神经网络算法，该算法只需一步就可计算出网络的输出权值，与传统的神经网络(如BP)和SVM相比，极限学习机的学习速度更快、精度更高。然而，极限学习机因为随机给定输入层权值和隐含层阈值，导致分类模型容易产生泛化能力和精度不理想等问题。文献[5-7]中分别采用差分进化和粒子群优化的混合智能算法、蝙蝠算法、生物地理学优化算法对输入层权值和隐含层阈值进行参数寻优，都取得了较好的效果。

本文对量子粒子群优化(quantum particle swarm optimization，QPSO)算法进行改进提出一种混合自适应量子粒子群优化算法(hybrid adaptive quantum particle swarm optimization，HAQPSO)用于对极限学习机进行优化，用优化后的极限学习机构建工业控制系统入侵检测模型。使用密西西比州立大学采集的天然气管道ICS网络层的工业控制系统标准数据集[8]进行实验研究，将本文算法与其它算法进行对比分析，验证了改进的有效性。

1 QPSO算法的改进

1.1 QPSO算法

QPSO算法具有量子的行为，由孙俊等[9]提出。算法将每个个体用量子空间的一个粒子来表示，在一个量子空间中，采用波函数ψ来描述粒子的状态，粒子的速度和位置同时确定不了，使用薛定谔方程确定粒子的位置概率分布。粒子的运动轨迹由蒙特卡洛随机模拟的方式可以得到，公式如下

(1)

式中：xid(t+1) 是粒子i在t+1次迭代时第d维的位置；当u>0.5时，±变为加号，小于或等于为减号；粒子随机位置用pi(t) 表示，计算公式如下

pi(t)=φd(t)pid(t)+[1-φd(t)]pgd(t)

(2)

式中：pgd表示种群的最优位置，pid是个体的最优位置，而φd是随机数，且在(0,1)之间均匀分布。

在QPSO算法中，势阱长度决定了粒子搜索的能力，用Lid(t) 表示，计算公式如下

Lid(t)=2α(t)|Cd(t)-xid(t)|

(3)

在Lid(t) 中引入平均最优位置，记为C(t)， 即

(4)

将式(3)代入式(1)就可以得到新的粒子进化方程

xid(t+1)=pi(t)±α(t)|Cd(t)-xid(t)|×ln[1/uid(t)]

(5)

在QPSO算法中，除去群体规模和迭代次数，式(3)和式(5)中的α是唯一的一个控制参数，被称为收缩—扩张系数。

1.2 QPSO算法的改进

1.2.1 改进参数α的控制方法

粒子的行为会随着收缩—扩张系数α的变化而变化。文献[10]中使用权重自适应改变的方法来改进PSO算法，取得较好的效果，受到启发，本文对于收缩—扩张系数α的控制，使用参数α自适应的方法，公式如下

(6)

根据文献[5]，式(6)中的αmax和αmin代表α的最大值和最小值，分别选取为1和0.5。f、favg和fmin分别为粒子当前的最佳个体适应度值、粒子的平均适应度值和最小适应度值。

当粒子的适应度值发生变化时，参数α会随着自适应变化。当各粒子的适应度值趋于一致时，参数α会自适应变大；反之，分散时参数α会自适应变小。

1.2.2 改进粒子随机位置的更新

差分策略是DE算法[11]的主要特性，本文结合DE/rand/1/bin差分策略对粒子随机位置的更新进行改进，改进公式如下

Pi(t+1)=P(r0)gd(t)+F(P(r1)gd(t)-P(r2)gd(t))

(7)

式中：F为缩放因子，根据文献[6]，F的较优取值范围为[0.4,0.9]。

本文同样采用参数自适应改变的方法来对F进行控制，公式如下

(8)

1.2.3 改进粒子位置的更新

Levy飞行策略是模拟鸟类搜寻食物过程的一种理想策略[12]，它是一种频繁的短距离蹦蹦跳跳和偶尔的长距离跳跃相结合的非高斯随机过程。短距离的蹦蹦跳跳保障了粒子在当前最好解周围内进行仔细的搜索以达到提高局部搜索的能力，长距离的跳跃则有利于保证粒子能跳出一个范围到另一个范围进行搜索，扩大了搜索空间，也就是增加了跳出局部最优的能力。许多学者利用Levy飞行策略的特性，在仿生学智能算法的进化方程中加入Levy飞行策略[13,14]，提高了算法的性能，优化效果也有一定的提高。本文对于粒子位置更新的改进是在方程中加入Levy飞行策略。

Levy飞行的步长与时间t服从Levy分布，幂指数形式的概率密度函数通过简化和傅里叶变换后就可以得到

Levy～μ=t-λ;1<λ<3

(9)

式中：λ为幂指数。因为用编程语言实现式(9)较为困难，所以经常使用的Levy飞行路径表达式如下

Levy(λ)=μ/|v|1/β

(10)

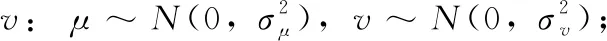
(11)

最终的Levy飞行路径Levy(λ) 将式(11)代入式(10)就能获得。加入Levy飞行策略后的QPSO算法粒子进化方程最终更新为

(12)

以下是HAQPSO算法的执行步骤：

步骤1 初始化粒子的位置，并将粒子个体最优位置初始化为当前位置；

步骤2 使用式(4)计算粒子群的平均最优位置；

步骤3 本文采取适应度最小原则计算出粒子当前的适应度值；

步骤4 同样采取适应度最小原则计算出种群当前的全局最优位置；

步骤5 使用式(7)计算出随机点的位置；

步骤6 使用式(12)计算出粒子新的位置；

步骤7 重复执行步骤2～步骤6，当满足设定的结束条件或达到最大迭代次数时停止。

1.3 HAQPSO算法的典型函数测试

为了验证改进算法的性能，本文使用两个典型函数作为算法的测试函数，使用MATLAB编写了相关程序，分析比较了HAQPSO算法与QPSO算法、PSO算法和遗传(genetic algorithms，GA)算法的仿真实验结果。设定上述几种算法的群体规模为20，最大迭代次数为2000，HAQPSO算法与QPSO算法的收缩—扩张系数α为[0.5，1]，缩放因子F的取值范围为[0.4，0.9]，根据各个测试函数的搜索边界确定粒子群体的初始位置，本文所用到的测试函数见表1，仿真实验结果如图1和图2所示(原图局部放大显示)。可以看出，HAQPSO算法的寻优性能要优于QPSO算法、PSO算法和GA算法。

表1 典型的测试函数

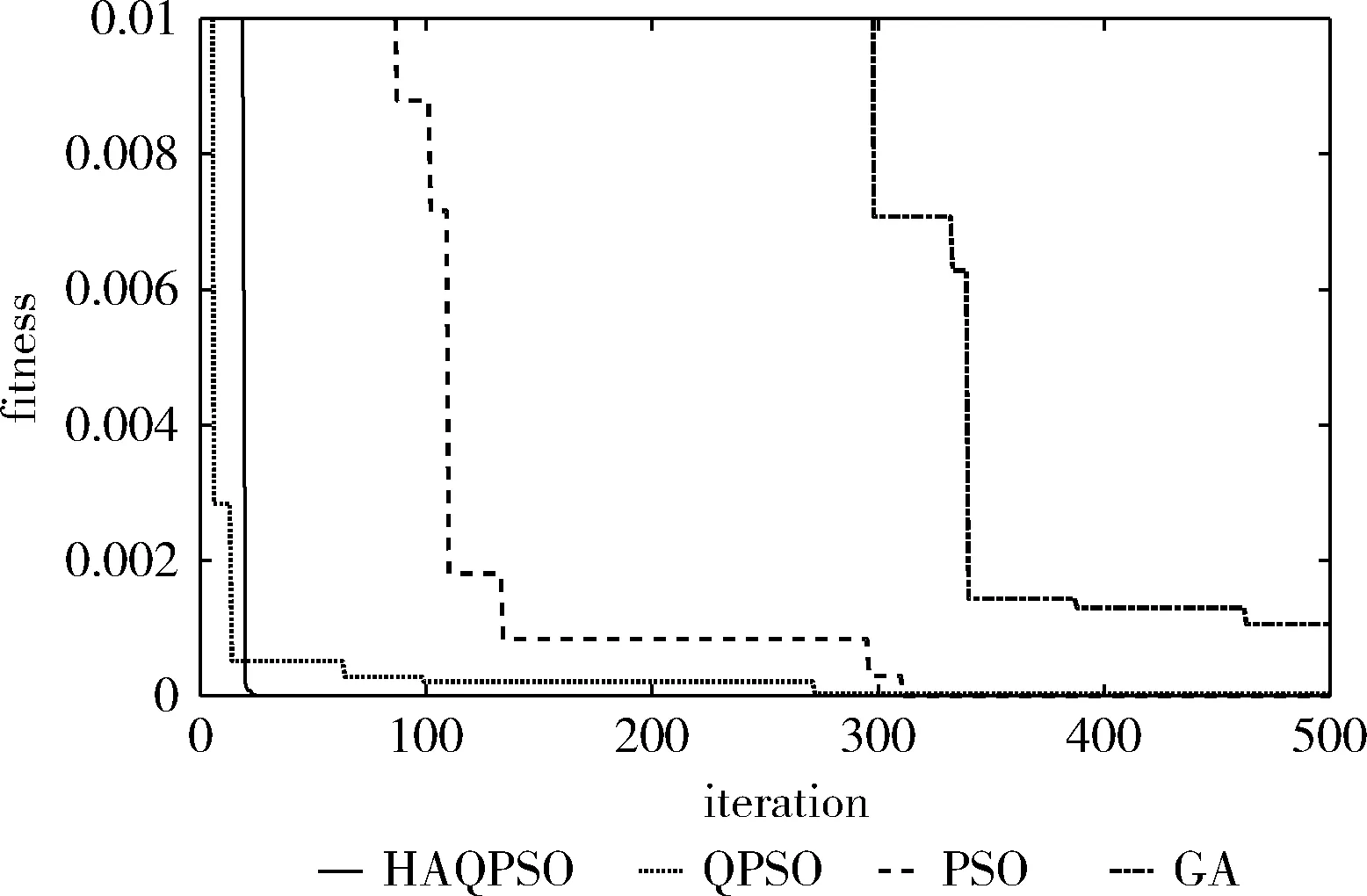
图1 Sphere函数迭代曲线

图2 Ackey函数迭代曲线

2 基于HAQPSO-ELM的工业控制系统入侵检测算法

2.1 极限学习机

极限学习机是新型的单隐层前馈神经网络。设定n、L和m分别为网络输入层、隐含层和输出层的结点数，有N个不同的训练样本 (xi,yi),1≤i≤N， 其中xi=[xi1,xi2,…,xin]T∈Rn，yi=[yi1,yi2,…,yim]T∈Rm， ELM的数学表达式可以表示为

(13)

式中：g(x) 为激活函数，ωi=[ωi1,ωi2,…,ωin]T为连接输入层到隐含层的输入权值向量，βi=[βi1,βi2,…,βim]T为连接隐含层到输出层的输出权值向量，bi为隐含层结点的阈值，Oj为网络输出值。

如果前馈神经网络能以零误差逼近这个N个样本，则有

(14)

此时存在βi、ωi和bi使得

(15)

用矩阵形式表示为

Hβ=Y

(16)

(17)

式中：H+为隐层输出矩阵的Moore-penrose的广义逆。

2.2 极限学习机的优化

由于ELM隐含层输出矩阵是由隐含层结点的阈值和随机给定的输入权值计算得出的，一些非最好的输入权值和隐含层结点的阈值的存在会导致极限学习机的分类容易产生泛化能力和精度不理想等问题。针对这个问题，本文采用混合自适应量子粒子群优化算法优化极限学习机的入侵检测模型，即通过混合自适应量子粒子群优化算法寻找到最好的输入权值和隐含层结点的阈值，进而计算出输出权值。HAQPSO-ELM入侵检测模型构建具体步骤如下：

步骤1 将数据集分为训练集和测试集，并进行归一化处理；

步骤2 初始化粒子群中的每个粒子的位置，并将粒子个体最优位置初始化为当前位置；

步骤3 使用式(4)计算粒子群的平均最优位置；

步骤4 将ELM的输入权值和隐含层结点的阈值作为优化的对象，适应度为分类准确率的相反数；

步骤5 根据适应度最小准则，使用HAQPSO算法进行迭代寻优，搜索出个体最好解和全局最好解；

步骤6 计算出随机点的位置；

步骤7 计算出粒子新的位置；

步骤8 重复执行步骤2～步骤7，当满足设定的结束条件或达到最大迭代次数时停止；

步骤9 选取搜寻到的最好的输入权值和隐含层结点的阈值构建ELM分类器模型，最终得到基于HAQPSO-ELM的工控入侵检测模型。

HAQPSO-ELM入侵检测模型构建流程如图3所示。

图3 HAQPSO-ELM的工控入侵检测流程

3 实验结果与分析

3.1 数据集

本文使用到的工控入侵检测标准数据集是密西西比州立大学关键基础设施保护中心于2014年提出的数据集，该数据集是对天然气管道仿真环境进行攻击而提取的网络层数据，且经过了数值化处理。该数据集中的每条数据都包含26个特征属性和一个攻击类别标签(包括正常数据标签)。

3.2 预处理

归一化处理：为了消除指标之间量纲的限制，将数据映射到[0，1]范围之间，转化为无量纲的纯数值之后就能进行比较。归一化公式如下

(18)

属性约简：使用Rosetta软件集成的粗糙集对数据集进行约简，约简后得到的属性共10项 {1,2,3,7,9,11,19,20,25,26}。

3.3 仿真参数的设定

为了验证HAQPSO-ELM在工控网络入侵检测中的性能，进行了仿真测试实验，所采用的实验平台：Inter Core i5 2.9 GHz，8 GB 内存，Windows 7，MATLAB R2016a。从原始数据集均匀且随机的抽取6000组数据，并将6000组数据分为训练集和测试集，数目分别为：4000和2000。HAQPSO算法需要设置的参数有：收缩—扩张系数α为[0.5，1]，缩放因子F的取值范围为[0.4，0.9]，Levy飞行的参数β为1.5。本文中HAQPSO算法和其它算法共同设置的参数有：最大迭代次数为50，群体规模为20，隐含层结点数为200，搜索范围为[-1，1]搜索维数d由隐含层结点数和输入层结点数决定，计算公式如下

d=NumberofHiddenNeurons* (NumberofInputNeurons+1)

(19)

3.4 仿真结果与分析

3.4.1 训练结果分析

为了验证算法的优化效果，本文将HAQPSO与QPSO、PSO、GA算法对ELM输入权值和隐含层结点的阈值进行寻优的结果进行比较。各个优化算法对ELM优化的运行时间和最终的优化精度见表2，在迭代寻优过程中，各代的训练分类准确率的迭代曲线如图4所示。

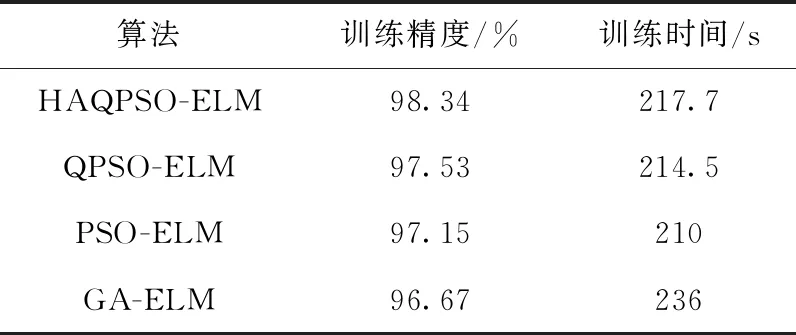
表2 训练时间和训练精度

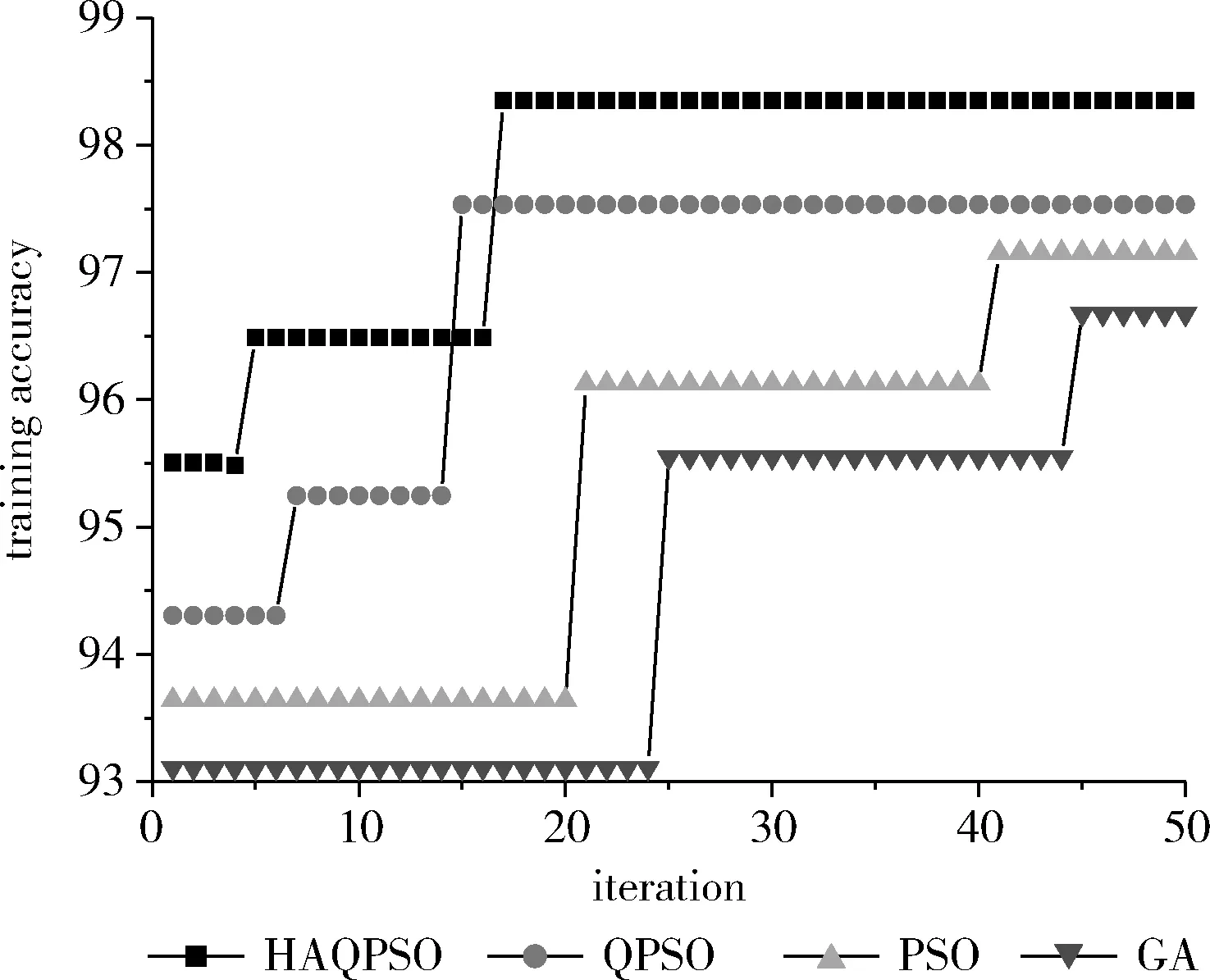
图4 不同算法优化ELM训练准确率曲线

从表2和图4可以得到，HAQPSO算法对ELM的寻优精度最高，达到了98.34%，而GA算法的精度最低，只有96.67%。QPSO在第15代左右就能够收敛到最好，收敛速度最快，HAQPSO在第18代左右能收敛到最好，仅次于QPSO。

从表2可以看出，HAQPSO训练时间比QPSO只增加了1.47%(3.2 s)，也就是说在QPSO算法的基础上加入Levy飞行策略、对粒子最优位置的更新采用差分策略和采用自适应改变的收缩—扩张系数控制方法对算法的整体运行时间增加的不多，只有3.2 s，也就是说对算法产生的影响并不大，并不会影响到算法的正常应用。

3.4.2 测试结果分析

(1)总体的检测效果分析。本文使用2000组测试集数据来测试训练所得到的ELM模型，因为实验数据集为不平衡数据集，对于不平衡数据的评价，使用准确率、精确率和召回率指标能更准确地评价算法的分类性能。实验的总体结果见表3。

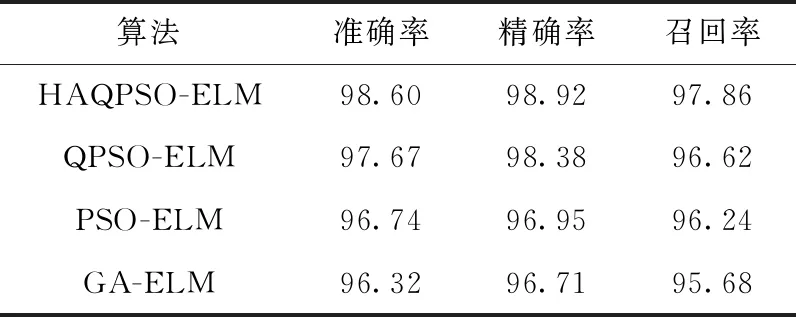
表3 总体检测结果

HAQPSO-ELM的准确率为98.60%，在所有的算法中准确率最高，而GA-ELM的准确率只有96.32%。同时，HAQPSO-ELM的精确率为98.92%，召回率为97.86%，在4种算法里都是最高的。综合各个指标可以发现，基于HAQPSO-ELM在构建的入侵检测系统具有良好的检测效果，具有较好的泛化能力，而GA-ELM的泛化能力最差。且外，本文也对标准ELM算法、SVM算法和BP神经网络算法在该数据集的分类结果进行了比较，结果见表4。

表4 其它算法检测结果

(2)各攻击类型数据检测效果分析。MSU工控入侵检测标准数据集包括4大攻击类，细分为8种攻击形式(包括正常数据)，各算法对8种攻击形式进行分类识别，分类准确率如图5所示。

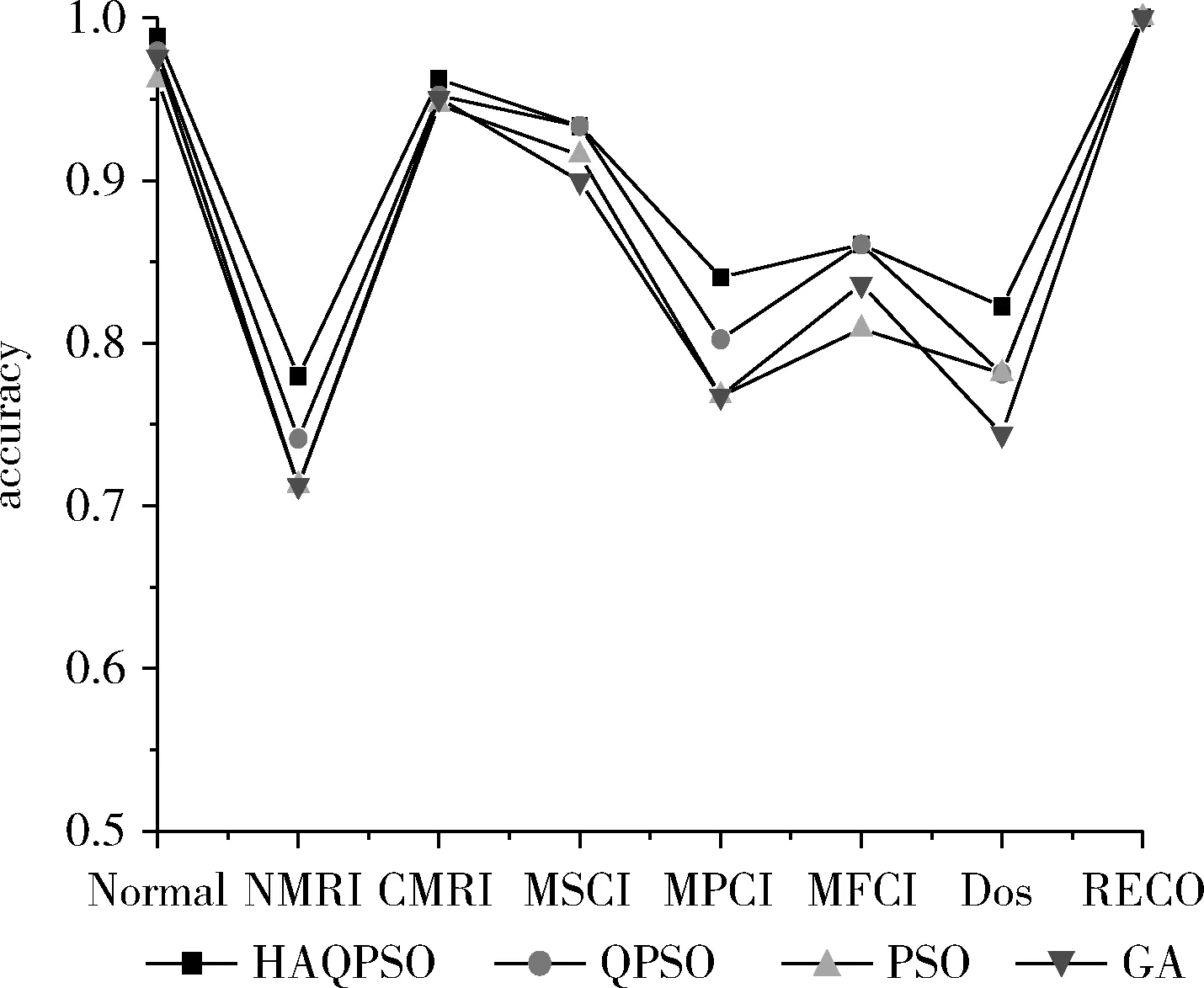
图5 各攻击形式分类准确率曲线

从图5可以看出，HAQPSO-ELM对每种攻击形式的都具有较高的分类准确率，尤其是在分类识别NMRI、MPCI、Dos上。HAQPSO与其它几种优化算法相比，HAQPSO-ELM入侵检测模型的分类准确率提升较高。且外，ELM入侵检测模型整体对Normal、CMRI、MSCI、RECO类别的数据分类准确率都较高，都在90%以上，特别是在对RECO攻击的分类识别上，各算法的分类准确率都接近100%，但是在对NMRI的识别上，识别准确率最好的都在80%以下。

4 结束语

本文对于QPSO算法的3点改进增加了种群多样性，较好解决了该算法易陷入局部最优的问题。通过HAQPSO算法对ELM的输入权值和隐含层结点的阈值进行寻优，构建基于HAQPSO-ELM的入侵检测模型。仿真实验使用的数据集为密西西比州立大学的工控入侵标准数据集，实验结果表明：HAQPSO-ELM的各项性能指标基本优于其它算法优化的ELM模型，验证了HAQPSO算法实际工程应用场景中的有效性。