无证书的多接收者匿名签密方案
2020-04-24祁正华吴振国王梦殊
祁正华,吴振国,王梦殊
(南京邮电大学 计算机学院,江苏 南京 210003)
0 引 言
对于传统的基于公钥的加密体制中存在的密钥及证书的管理问题,Shamir提出了基于身份的公钥密码体制,一度成为众多学者研究的热点,目前已有很多基于身份的加密、签密方案被提出[1-4],但基于身份的密码体制中的方案存在一个严重的问题即密钥托管的问题。Al-Riyami和Paterson提出了一个没有证书的公钥密码体制,无证书密码体制很好解决了上述两种密码体制当中存在的问题,国内外学者相继提出了很多适用于网络传输、无线传感等新型网络传输环境下无证书加密、签密算法[5-10]。
多接收者签密是指将消息经过签密之后发送给多个授权接收者的过程。国内外很多学者提出了多种新的多接收者签密方案,然而大多签密机制[2-4,11]都是基于身份的密码系统,其中存在密钥托管的问题,文献[4]是多接收者单一消息签密;文献[11]中收件人的标识列表或密文标记列表是密文的一部分,因此签密容易暴露收件人的身份;文献[12]是聚合签密方案,是多对一模式,文献[13,14]都是周的方案,文献[15,16]需要计算索引,且是单一消息通信模式,若进行多消息发送模式,效率低下;文献[17-20]部分存在匿名不公平性问题,也就是说,整个加密过程中只考虑到接收者的匿名性问题而忽略了发送者匿名性问题。
针对以上方案存在的问题,本文提出一种无证书多接收者匿名签密方案,方案同时保证了发送者和接收者的匿名性,并且具有较高的解签密效率和较低的通信开销,采用Lagrange插值公式和离散对数(DL)问题来证明文中的保密性,具有不可伪造性和匿名性。
1 相关基础
1.1 离散对数问题及Lagrange插值多项式
离散对数问题(discrete logarithm problem,DLP)对于给定的A,B∈G, 通过计算找到等式B=nA成立的整数n, 其中G是阶数为素数q的循环群。
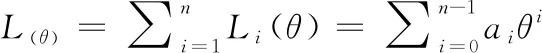
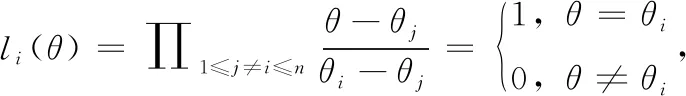
1.2 无证书多接收者签密方案的安全模型
基于无证书的签密方案一般会面临两种攻击:第一种攻击类型是恶意用户A1。 攻击者A1并不知道用户的主密钥,但是他能够对合法用户的公钥进行替换;第二种攻击类型是恶意的KGC攻击者A2, 这一类敌手虽然能够掌握系统主密钥,攻击者A2与攻击者A1恰好相反,他有能力知道用户的主密钥,但是无法替换用户的公钥。我们通过以下的几个定义来简单说明多消息多接收者签密方案的安全模型。
定义1 第一种攻击类型的机密性:如果不存在上述的第一种恶意攻击用户A1能够在有界多项式时间内以显著优势赢得以下游戏,那么就可以称在适应性选择密文攻击下该多接收者签密方案满足不可区分性。
系统建立:我们假设挑战者为D, 第一种恶意攻击敌手为A1,将params发送给A1。
第一轮询问:A1可以对D产生以下的询问:
私钥生成查询:A1输入任意用户及其身份信息 (Xi,IDi) 进行问询,挑战者通过私钥生成算法得到这个用户的私钥SKi=(xi,yi), 然后将这个私钥反馈给敌手A1。
替换公钥查询:A1输入任意用户及其公钥信息(IDi,PKi),PKi=(Xi,Yi), 挑战者根据查询到的该用户的公钥选取另一个公钥PK′i=(X′i,Y′i), 将这个用户的原始公钥替换为新选取的替换公钥。
签密查询:A1根据需要查询的明文集合M={m1,m2,…,mk}, 所有的接收者U={ID1,ID2,…,IDk} 的公钥信息及签密者身份IDA的私钥信息,对D进行签密查询,D则生成有关签密者IDA, 接收者IDi∈U(i∈{1,2,…,k}), 公钥PKi的密文σ=Signcryption(params,M,U,SKA), 然后将这个密文反馈给A1。
解签密查询:A1根据需要查询的密文σ, 所有的接收者的私钥信息及签密者身份的公钥信息,对D进行解签密查询,D根据以上信息通过解签密算法Unsigncryption(params,M,U,SKA) 将密文σ还原成明文消息集合M, 然后将还原出的明文消息集合M反馈给A1。
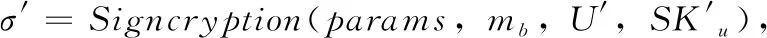
猜测:A1进行与上述多个询问类似地多项式有界次询问,但不能够对所有接收者当中的任意接收者进行私钥查询和对密文σ进行解签密查询。完成上述过程后,输出一个b′作为对b的猜测,若b′=b, 那么说明A1获得本次游戏的胜利,取得游戏胜利优势为AdvCMRS(A1)=|Pr[b′=b]-0.5|。
定义2 第二种攻击类型的机密性:如果不存在上述的第二种恶意攻击用户A2, 能够在有界多项式时间内以显著优势赢得以下游戏,那么就可以称在适应性选择密文攻击下该多接收者签密方案满足不可区分性。
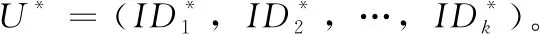
第二轮查询:A2实施与第一轮相同的查询,但不包括第一轮的第二个查询。
私钥生成查询:A2输入任意用户及其身份信息 (Xi,IDi), 挑战者通过私钥生成算法得到这个用户的私钥SKi=(xi,yi), 然后将这个私钥反馈给A2。

解签密查询:A2根据需要查询的密文σ,所有的私钥信息及签密者身份的公钥信息,对挑战者D进行解签密查询,挑战者D通过解签密算法Unsigncryption(params,σ,U,SKA) 将密文σ还原成明文消息集合M, 然后将还原出的明文消息集合M反馈给A2。
最后敌手A2进行和阶段一相同的挑战和猜测。
定义3 第一种攻击类型的不可伪造性:如果不存在上述的第一种恶意攻击用户A1能够在有界多项式时间内以显著优势赢得以下游戏,那么就可以称在适应性选择密文攻击下该多消息多接收者签密方案满足不可伪造性。
系统建立:我们假设挑战者为D, 第一种恶意攻击敌手为A1, 挑战者运行初始化算法,将生成的公共系统参数反馈给敌手。
训练:A1对挑战者实施如第一轮询问相同的查询。
定义4 第二种攻击类型的不可伪造性:如果不存在上述的第二种恶意攻击用户A2能够在有界多项式时间内以显著优势赢得以下游戏,那么就可以称在适应性选择密文攻击下该多消息多接收者签密方案满足不可伪造性。
系统建立:我们假设挑战者为D, 第二种恶意攻击敌手为A2, 挑战者运行初始化算法,将生成的公共系统参数反馈给敌手。
训练:A2对挑战者实施如第二轮询问相同的查询。
2 无证书多接收者签密方案
本文提出的签密方案分为以下5个阶段:
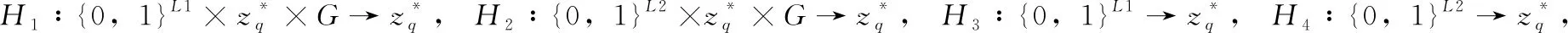
(2)用户公钥提取阶段:用户IDi根据随机选取的xi, 生成公钥Xi=xiH3(IDi);

(4)多接收者签密阶段:用户UA对发送给IDi消息mi签密如下:
2)计算拉格朗日差值多项式
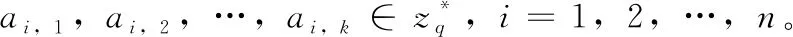
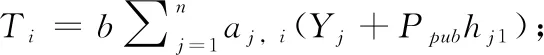
4)计算hi,2=H2(IDA,VA,XA,Zi), 其中Zi=(b+yA)(Yi+Ppubhi1),Wi=(IDA‖mi)⊕hi2;
5)计算Ri=H4(IDA‖mi);
6)计算Si=b+(XA+yA)Ri, 这样σi=(VA,T1,T2,…,Tn,Wi,Si) 为uA对IDi消息mi的签密。最后形成的密文消息是δ={T1,T2,…,Tn,VA,W1,W2,…,Wn,S1,S2,…,Sn}, 然后以广播的形式发送给每一位接收者。
(5)解签密阶段:IDi对uA发送的签密进行解签密,步骤如下:
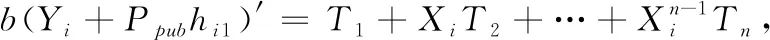
2)计算(IDA‖mi)=Wi⊕hi2;
3)计算hi1=H1(IDi,Xi,Yi);
4)计算Ri=H4(IDA‖mi) 并通过等式对SiP=VA+(XAP+YA+ppubhi1)Ri进行验证,若正确则输出对应消息 (IDA‖mi), 否则无效。
正确性验证:
对接收到密文进行如下验证:
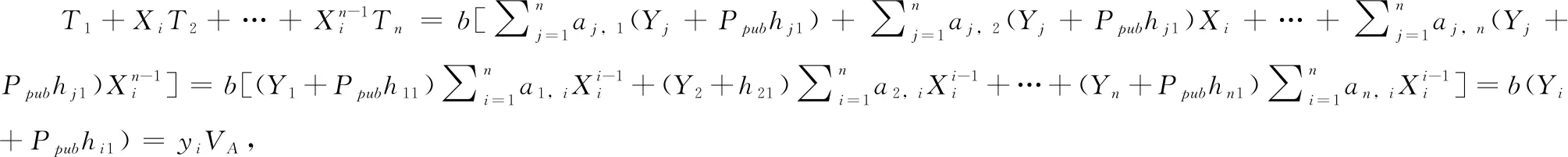
如果:SiP=[b+(XA+YA)Ri]P=VA+(XAP+YAPpubhi1)Ri则验证正确,接收对应消息(IDA‖mi)。
3 安全性分析及效率分析
3.1 安全性证明
在随机预言机模型下,对于本文所提出的无证书的多消息多接收者匿名签密算法的安全性证明也分别从两种类型的攻击下进行机密性和不可伪造性这两个方面的证明。
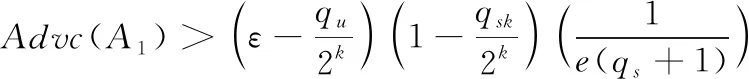
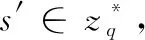
第一轮查询:
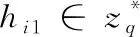
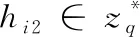
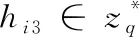
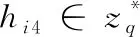
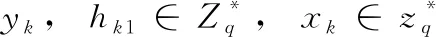
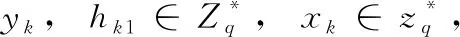
公钥替换查询:敌手A1想要获得用户IDk的公钥替换查询,挑战者D在Lpk中查找 (IDk,xk,PKk), 然后将替换的 (IDk,*,PK′k) 插入到Lpk中,最后把结果反馈给敌手。
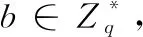
解签密查询:敌手A1通过挑战者D对签密
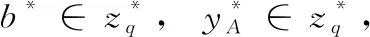
第二轮查询: 敌手实施和第一轮查询相同的步骤,但不包括H1-查询、私钥查询和解签密查询。
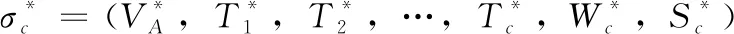
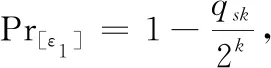
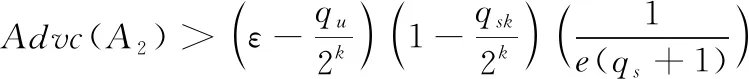
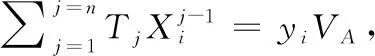
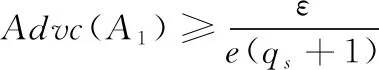
证明:过程与定理1的方法类似。
查询:敌手实施定理1中一样的两轮查询。
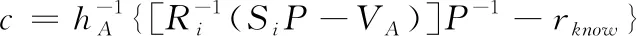
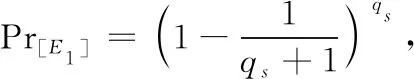
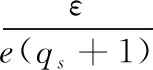
证明:过程与定理2的方法类似。
查询:敌手实施定理2中一样的两轮查询。
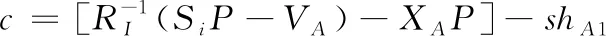
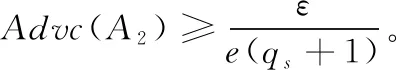
3.2 机制分析
针对本文提出的无证书的多接收着匿名签密方案分别从匿名性、多消息签密以及公开验证这3个方面进行机制分析。
(1)匿名性
本文方案同时保护了发送者身份和各个接收者身份的匿名性。发送者匿名性的实现是将发送者的身份信息插入到Wi中,只有授权的合法接收者才能够通过签密密文知道发送者的身份信息;接收者匿名性的实现是将接收者的身份信息插入到拉格朗日插值多项式当中,并且其它接收者也无法得知除自己以外的其它接收者的身份信息。
(2)多消息签密
本文所提出的多签密算法不仅可以将同一个消息发送给多个接收者,也可以将多个不同的消息发送给不同的接收者,实现方法是将需要签密的明文信息插入到Wi当中,满足当前网络通信多消息发送的需求。
(3)公开验证性
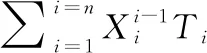
3.3 效率分析
将本文提出的签密方案与参考文献[13-20]提出的方案进行效率分析对比,主要从解签密的运算量以及签密方案后的密文长度两个方面来分析,解签密的运算量主要影响解签密过程的效率,密文的长度直接影响密文传输的通信开销和系统存储。本文方案和其它方案中签密及解签密过程中计算耗时比较大的主要有3个运算,分别是双线性对运算、指数运算和点乘运算,为了描述方便,将这3个运算分别用Ed、Ex和Mt表示,其中计算时间规则如下,Ed>Ex和Ed>Mt。
从表1可以看出,文献[13,17]在进行单消息签密时的计算效率较高,但在进行多签密运算时,其解签密效率会随着解签密人数的增加而增加,从而导致效率低下。本文中签密方案可进行多消息签密,且无需双线性对运算,文献[15,16]在解签密过程中均需要运用双线性对运算,大大增加了运算量;文献[18]在签密过程中需要对每个不同的接收者的身份信息进行索引计算,降低了签密的速率;而文献[19]虽然在签密和解签密过程中的计算量较小,但是该方案无法对多个消息同时进行签密;文献[20]在签密中需要使用双线性对运算,并且运算量较大。由此得知,本文设计出的多接收者匿名签密方案具有更高的签密和解签密效率。

表1 签密方案运算量比较

表2 签密方案密文长度比较
综上所述,本文方案与现有的签密机制相比较,在完成多消息多接收者签密的同时,具有较高的解签密计算效率和较低的通信开销。
4 结束语
本文对比以前的多接收者签密方案,保证方案在随机预言机模型下具有可证安全性的基础上,采用拉格朗日插值方法提出了无证书的多接收者匿名签密方案,该方案在签密过程中不需要双线性对运算且是多消息多接收者签密,具有较高的解签密计算效率和较低的通信开销,方案具有匿名性、公开验证性、机密性和不可伪造性。对于移动支付、无限网络传输以及金融行业等和敏感信息传输方面的行业具有较强的实用价值。
