多阶段多目标动态测试资源分配算法

牛福强，张国富,2，苏兆品,2，岳 峰

(1.合肥工业大学 计算机与信息学院，安徽 合肥 230601；2.合肥工业大学 工业安全与应急技术安徽省重点实验室，安徽 合肥 230601)

0 引 言

获得高质量和满足市场需求度的软件是软件测试最为重要的目标，软件测试利用消耗测试资源检测软件故障，发现并修复软件漏洞是获取高可靠性软件的必要途径[1,2]。软件测试消耗的资源接近软件开发总资源的一半[3]。随着基于搜索的软件工程的迅速发展[7]，一些演化计算技术被用来求解测试资源分配问题[8,9]，如遗传算法[10]、蚁群优化[11]。

在现实环境当中，软件测试是动态的、不确定的，同一个测试模块在不同测试阶段所展现出的特征也有差别。软件系统中的模块错误数量在测试行为执行前已经被预估，其每个模块相关参数和分配到的测试资源也不会随着错误的发现、前期测试阶段获得的经验而进行相应的调整，这种静态环境下的最优化测试资源分配问题在以往工作中[4-6]进行了非常全面的研究。Zeephongsekul等[12]通过统计历史阶段的发现的错误数量以及检测出每个错误的时间点对下一个阶段的模块参数利用极大似然估计进行了重估。Chaudhary等[13]针对最大化检测错误数的优化问题提出了一种基于差分进化算法的多阶段测试资源分配算法(MS-DE)。陆阳等[14]采取将测试资源划分成多个阶段分配给软件系统，阶段资源可以根据每个模块的可靠性进行相应的调整，以便帮助解集更快收敛。但是模块参数并没有根据检测出的错误数进行参数的重估，仍然属于测试行为未发生的静态环境下，所进行的多阶段测试资源的预分配，与实际中的测试存在较大的差异，不符合动态测试资源分配中的动态属性。

本文结合了传统研究中基于演化算法多个目标同时优化的特点以及动态测试资源分配中的基于历史信息动态调整模块参数以及每个测试阶段的测试资源。测试人员可以根据实际的需求在每个测试阶段获得的目标解集中选出偏好解，根据该偏好解执行测试并收集相关的错误信息，收集到的错误信息将会用于之后的测试阶段参数的估计，从而使下一阶段优化中获得符合实际的解决方案。并且能够基于实际情况将有限的测试资源分配需求度高的模块，从而获得满足市场需求的高可靠性软件系统。

1 问题描述

图1 总的可用测试时间多阶段划分

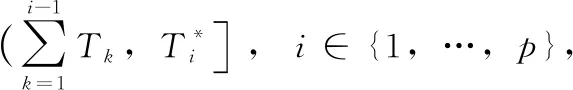
(1)

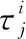
在每个测试阶段执行前，测试管理者都要从当前阶段算法给出最优解集选取一个最符合当前市场需求或者高可靠性的偏好解作为执行方案。而该偏好解给出总消耗的测试时间必定小于或等于该测试阶段可用的总测试时间，因此在第i阶段可用的总测试时间与实际消耗的测试资源之间的关系满足

(2)

(3)

可以求解上述一阶微分方程，我们可以发现模块j在阶段i中平均检测到的错误数与消耗的测试时间呈指数关系，如下

(4)

在衡量软件系统质量的标准中，软件内平均每个模块剩余错误数量是软件可靠性最为直接、有效的表述。每一个模块在软件系统中的相对重要程度随着测试阶段的不同而有所不同，可以根据需求进行相应的调整。软件系统在第i个测试阶段的剩余错误总数为

(5)

综上所述，为能够获得满足市场需求的软件系统，在每个阶段给予可用消耗的测试时间以及软件系统剩余的错误总数双重约束下，力求最小化软件系统错误总数以及最小化测试时间消耗，从而形成多阶段、两目标、动态求解测试时间分配优化问题模型

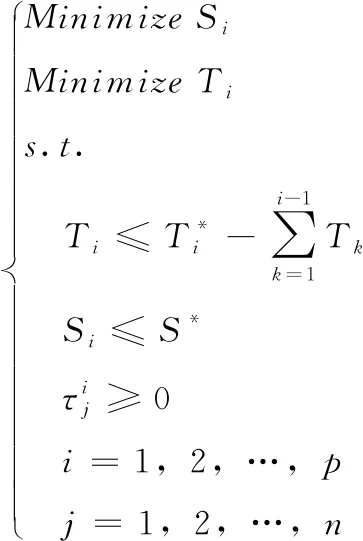
(6)

2 多阶段NSGA-II动态分配算法

2.1 NSGA-II

多目标优化算法NSGA-II[10]是最为经典的演化算法之一，该优化算法的性能已经在以往的研究以及工程实践中得到广泛的认可。NSGA-II能够简单有效选取全局最优解，并且在同时优化两个目标问题模型中具有较大的优势。经过研究人员不断研究，NSGA-II的性能也变得更加完善，但该算法的整体框架和基本思想没有改变。多目标算法NSGA-II针对两个目标双重约束问题基本框架为：在测试时间限制范围内生成规模为N的初始种群，即含一个有N个解的解集，该N个解是随机生成、广泛分布的，对初始种群进行非支配排序，非支配排序的原则是在两个目标能够支配其它解排在上层，称之为非支配解；在目标中各有优劣，将会排序分布在同一层。然后在非支配排序后种群中利用二进制锦标赛选择两个父代个体，进行二进制交叉以及多项式变异的遗传操作，从而产生两个子代个体。将父代与子代个体进行合并，种群大小为2N，对合并后的种群进行非支配排序，非支配排序过程中，不只通过两个目标的最优程度进行判断，还需要加入个体违背约束的程度，一个个体违背约束的程度越高，得到的排序位置越靠近下层，淘汰的几率也就越高。然后根据非支配排序的位置选取N个子代种群，不同层的选择上层，较优的非支配解将容易保存下来；同层之间计算拥挤距离，保留拥挤距离相对较大的，从而保证子代种群的多样性。通过非支配关系以及拥挤距离保持子代的精英性以及多样性。子代总是能够支配父代，重复上述步骤，不断趋近Pareto前沿[14]，直到满足算法终止条件。具体流程如图2所示。二进制锦标赛选择、模拟二进制交叉和多项式变异3个基本操作的具体细节请参照文献[16]，这里不再赘述。

图2 NSGA-II算法流程

2.2 参数估计

(7)

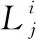
(8)

利用上述的对数似然函数可以得到如下的微分方程组

(9)

2.3 种群重新初始化

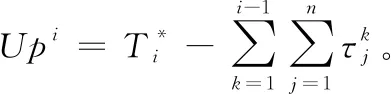
2.4 约束处理

根据上一节编码方式和种群初始化，我们不难发现即使个体中的每个元素符合约束条件，个体有可能不符合约束式(6)中约束条件。除此之外，根据演化算法的迭代进化过程中，遗传操作包括交叉操作、变异操作都有可能导致个体中的元素以及个体违背上述的约束条件。尽管演化算法能够淘汰不符合约束的个体，大量的违规个体通过遗传操作将会大概率产生的违规的子代，不利于种群的进化，减慢种群的收敛速度。因此我们需要对个体中的元素以及个体进行测试时间上的约束，帮助算法快速收敛。本文对种群初始化以及交叉、变异操作后，对种群中的每个个体以及个体元素进行密切监控，若存在违背约束条件则对编码进行修正，具体修正思路如下：

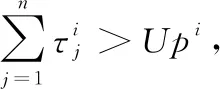
上述约束处理能够减少违规解的参与遗传进化当中，有利于加快种群进化的收敛速度；另外这种约束处理添加了随机性能够保证个体的合法性，又能够保持种群的多样性。

2.5 算法描述

综上所述，我们将参数估计、种群初始化以及约束处理与传统的NSGA-II相结合产生多阶段两个目标动态测试时间分配算法(MS-NSGA-II)，该算法的整体思想是，能够解决同时优化两个目标、双重约束下的测试时间分配问题。测试管理者可以根据偏好选取符合实际的解，根据偏好解动态调整后续测试阶段的可用测试时间。

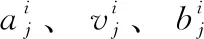
图3 MS-NSGA-II多目标动态测试时间分配算法流程

3 实验结果与分析

3.1 实验参数和评价指标

在进行实验验证之前，我们需要配置相应的软件系统模块参数以及算法相关参数。

表1 模块的初始参数

在本文中我们结合了两个目标模型和多阶段的特性，为了说明所提出的MS-NSGA-II的优点，将采用动态单目标MS-DE[13]和静态多目标NSGA-II与其对比，3种算法所用到的参数见表2。

表2 算法的基本参数

另外，我们需要对算法的结果进行处理和评估，以便比较算法之间的优劣。评价多目标优化结果的两种经典标准容量值(capacity)和满足客户解的标准覆盖指标[10](standard cover metric)。容量值是表示算法解集中满足一定标准的解的数量，数量越多算法性能越好；覆盖指标是解集A中的解覆盖解集B中所有解的百分比，百分比大的算法性能优良。

3.2 与动态单目标的对比

在该部分实验当中，我们比较MS-NSGA-II以及MS-DE两种算法。首先针对30(n=30)个模块的软件系统进行实验，另外还需要将总的测试时间分为3个测试阶段(p=3)：[0,70 000]、[70 000,130 000]、[130 000,200 000]。MS-DE为单目标优化，因此只针对式(6)中的Si优化。每个阶段检测出的错误数根据式(4)的值附近随机给出，两种算法保持一致。每个阶段的偏好解设置剩余错误数最少的(MS-DE只能获取该类型的解)。将所获得的最终解集进行画图，如图4所示。由图可以看出，MS-DE优化后获得一个单解，而MS-NSGA-II每个测试阶段都会获得一个解集，最终解集中有相当一部分解的系统剩余错误数少于MS-DE的单解。因此我们可以得出MS-NSGA-II能够提供多个候选解的同时，系统剩余错误数量最少的解优于MS-DE的单解。

图4 MS-DE和MS-NSGA-II得到的解集

为了更加凸显出MS-NSGA-II的优点，我们以MS-DE的单解作为偏好解，在MS-NSGA-II的解集中挑选出好于该偏好解(Si目标值小于等于4.457 99)统计数量，并且将剩余错误数最小的列见表3。由表3中数据可以得到无论从解的质量以及数量，MS-NSGA-II的解集都要优于MS-DE的单解，因此MS-NSGA-II的算法性能要好于MS-DE。

表3 系统剩余错误数苛刻阈值下的解

3.3 与静态多目标的对比

同样我们针对30个模块系统进行测试时间分配，NSGA-II和MS-NSGA-II两个算法的之间的性能。由于NSGA-II为静态环境下的测试时间分配，所以只有一个测试阶段；在此部分为了说明多阶段的优点我们将MS-NSGA-II的测试时间划分成4种环境：2个、3个、4个和5个测试阶段与NSGA-II进行比较，每个测试环境各测试阶段的测试资源划分见表4。

表4 每个测试环境的阶段数和测试时间划分

针对两种算法每个环境进行30组的实验，选取其中一组实验画图，如图5所示。由于两个算法都获得是解集，因此可以从图中看出两个解集汇成不同的曲线，该曲线能够说明测试时间和剩余错误数之间的关系。另外4种环境下MS-NSGA-II的米子点解集处于NSGA-II点解集的下方，通过支配关系的比较，我们能够得出MS-NSGA-II的解集要好于NSGA-II的解集。另外我们看出测试阶段数越多解集的质量并不一定好，在环境3、4中的解集质量不如环境1、2中的解集质量。MS-NSGA-II解集好于NSGA-II原因在于多阶段的参数估计形成正反馈，可以将有限的测试时间分配给更需要的模块，因此表明MS-NSGA-II的性能优于NSGA-II。为了说明算法能够动态调整各个测试阶段的测试时间，充分的利用测试时间，我们在环境4中(p=5时)选取两个模块，将测试阶段和每个阶段分配到的测试时间画图，如图6所示。从图中我们可以得到，模块1在前面阶段分配到的测试资源较多，也就是可靠性达到一定时，算法将不会再把测试时间分配给该模块。模块2在前面测试阶段分配到的资源较少，可靠性较低，算法通过调整在后期测试阶段分配给该模块的资源增多。因此MS-NSGA-II算法具有动态调整资源的功能。

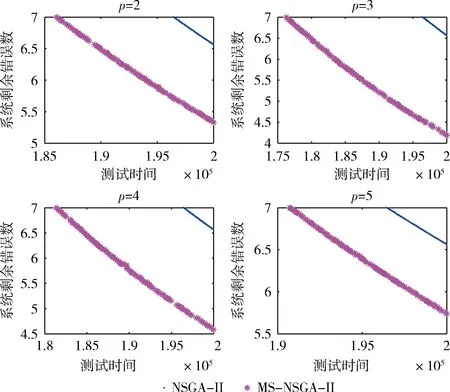
图5 NSGA-II和MS-NSGA-II得到的解集

图6 每个阶段分配的测试时间

另外，以上比较了两种算法整个解集的比较，我们还需要采用更为严格的标准比较两种算法的性能，即设置更为严格的阈值解Si≤6.6下的两种算法容量值之间的比较，以及符合严格阈值解的覆盖值比较。经过30次实验结果进行统计平均见表5，由表所得MS-NSGA-II得到的平均容量值要大于NSGA-II，尽管在测试环境4中，MS-NSGA-II略大于NSGA-II，说明在相同的实验环境当中，MS-NSGA-II多阶段反馈能够帮助解集快速收敛的特点，从而获得的更多的满意解。在30次实验中挑选出Si≤6.6的解完成覆盖值的比较并进行统计分析，我们给出了覆盖值的均值和标准差, 并基于Wilcoxon Rank Sum检验[17](0.05的显著性水平)进行显著性分析，用黑体标出差异显著的最佳均值。如表6所示，在测试环境1、2、3中MS-NSGA-II覆盖值要明显优于NSGA-II，说明在前3个测试环境中，MS-NSGA-II能够挖掘到了更好的测试时间分配方案。但是，在测试环境4中MS-NSGA-II并没有表现出较大的优势。综合图5以及表5、表6中数据，容量值和覆盖值都有所下降，因此得出测试阶段数量增多并不能够帮助获得高质量的解集。原因在于总的迭代次数是有限的，测试阶段数增加，每个测试阶段的迭代次数减少，各阶段的解集并没有达到算法收敛需求。

表5 NSGA-II和MS-NSGA-II的平均容量值

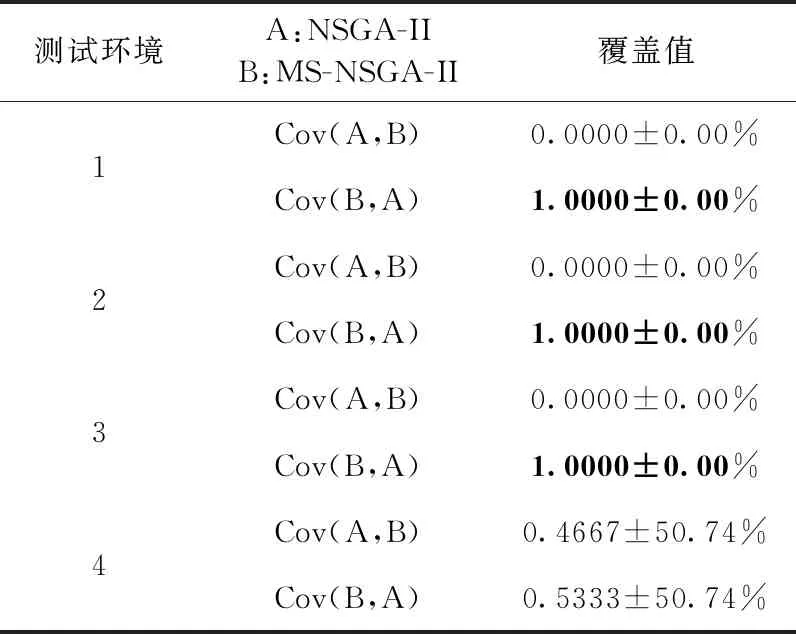
表6 NSGA-II和MS-NSGA-II的覆盖值(均值±标准差)

4 结束语

软件测试消耗大量的测试资源，本文将动态优化以及多目标相结合，提出一种基于NSGA-II的多阶段两个目标动态测试资源分配算法。该算法兼具了动态测试资源多阶段正反馈的属性以及多目标同时优化的优点，其中参数估计、种群初始化以及约束处理能够自适应调整每个测试阶段的测试资源帮助解集快速收敛。通过与动态单目标MS-DE和静态多目标NSGA-II的对比实验分析，MS-NSGA-II能够提供更多更高质量的测试资源分配方案。在未来的研究中，我们将致力于如何合理的划分测试阶段。