基于Mindlin解的盾构隧道施工地表变形及参数敏感性分析

杨玉平,刘运思,牟天光,李小雷,屈军平,周小龙,王晶,周国民

(1.中铁北京局集团 (天津)工程有限公司,天津,300000;2.湖南科技大学 岩土工程稳定控制与健康监测省重点实验室,湖南 湘潭,411201;3.湖南科技大学 土木工程学院,湖南 湘潭,411201)

近年来,随着国家经济的日益发展,城市人口不断增长,市内交通拥堵现象严重,而城市可利用交通建设的土地有限。因此,地下空间的利用日趋重要,地铁建设是缓解市内交通拥堵的方法之一。然而,地铁隧道周边建筑物密集或位于道路下方,对控制地表变形要求较高,尤其在不良地质地区,隧道施工过程中,地表容易出现隆起或下沉,甚至会造成地面坍塌,这就跟给现场盾构施工带来极大的风险。纵向地表变形规律是盾构隧道掌子面前后土体空间约束效应的直观反映,预示着掌子面的稳定,以及盾构机推进过程中围岩的稳定情况。因此,开展盾构施工纵向地表变形特征的研究具有极其重要的意义。目前,国内外一些学者对盾构隧道施工地层变形进行了相关的研究,如吕玺琳等[1]和黎春林等[2]对地铁盾构隧道施工过程掌子面稳定和土体扰动情况进行数值模拟,考虑了壁后注浆参数、土体的塑性区等因素,但是没考虑盾壳外壁与围岩之间的摩擦力引起的土体变形。颜波等[3]、叶飞等[4]和何川等[5]对影响盾构法隧道施工引起地层变形的土层参数做了相关研究,得出控制地表沉降的措施,但未揭露纵向地表变形的规律。程红战等[6]和王长虹等[7]考虑岩土参数空间随机性在盾构施工地表沉降的影响,进行了相关的理论分析,得出地表沉降近似服从对数正态分布,但未考虑盾构推进过程中开挖仓压力对地表变形的影响。Mindlin[8]提出弹性体在力的作用下空间某一点的变形的理论计算方法。MIRO等[9]和MOLLON等[10]考虑地层参数随机性对地表变形影响进行了概率统计分析。部分学者[11-16]利用peak公式,通过大量的工程监测资料进行分析,得出盾构隧道地表变形的弹性解。

综上所述,本文基于Mindlin解,引入摩擦角φ,推导了盾构施工过程纵向地表变形的弹塑性解析解,开展盾构施工过程纵向地表变形规律研究,获得盾构施工隧道中线上方纵向地表变形特征,以及地层参数对纵向地表变形的影响,为盾构施工前进行风险预测及地表变形对周边构筑物的影响提供参考。

1 基于Mindlin解盾构施工纵向地表变形理论分析

1.1 盾构施工中地表变形分析

根据弹性力学R.Mindlin解,当土层为均质各向同性半无限弹性体,则在距表面某一深度H点作用有水平集中力P时的任意一点(x,y,z)的竖向位移可采用Mindlin解。水平力作用下地层竖向变形简图如图1所示。假设本模型土层为均质各向同性半无限弹塑性体,土体的变形是由于土颗粒间的位置发生变化,这样土层的变形表现为非线性,弹塑性土体的变形与其抗剪强度有关,而内摩擦角是土体抗剪强度的重要参数,因此可假设弹塑性土体的变形与其内摩擦角的正切值存在联系,基于Mindlin解,对弹塑性土体在水平均布荷载作用下对地表产生的位移进行积分,得到水平均布荷载作用时,隧道中心线上方纵向地表任意一点的竖向位移。本模型假定盾构施工在模拟计算的里程范围内沿直线推进,不考虑盾构施工纠偏、调线调坡、管片变形等引起的地层损失。

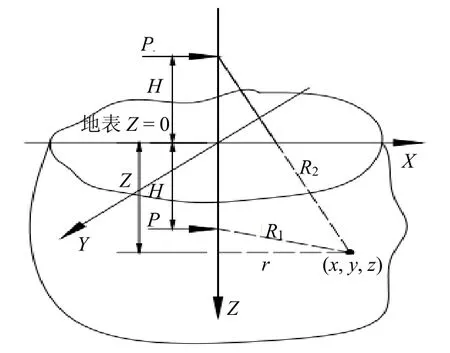
图1 水平力作用竖向地层变形简图

2.2 掌子面附加作用应力引起的地表竖向变形

假定盾构机推进过程在隧道掌子面施加的开挖仓压力为圆形均布荷载P(kPa),掌子面侧向静止土压力为F(kPa),得到施加在掌子面的附加作用应力(现场施工时ΔP一般控制在±20 kPa,本文取附加作用应力为20 kPa。基于Mindlin解,取掌子面均布荷载微元作用引起的地表某一点的竖向位移为dz,对掌子面区域的均布荷载作用引起的地表竖向位移进行积分,得到隧道中心线上方由掌子面附加作用应力引起的地表竖向位移变形量z1。

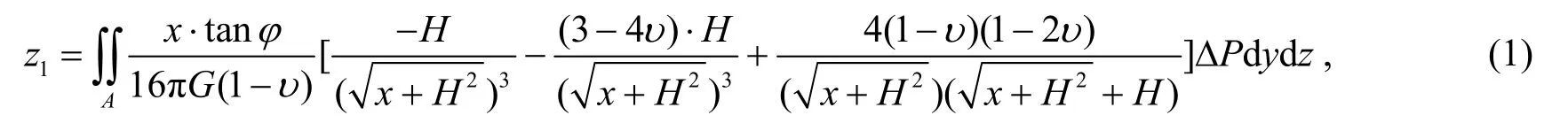
式中：z1为隧道中心线上方某一点的地表位移变形量,H为均布荷载作用的重心到地表X轴的距离,G为土体剪切弹性模量,,E为变形模量,υ为泊松比,ϕ为内摩擦角,A为隧道掌子面面积,(x,y,z)为所求位移点的坐标。

2.3 盾壳外圆周侧壁与隧道围岩之间的摩擦力作用引起的地表竖向变形

取盾构机外圆周侧壁外表面的微元面积Rdθdl,基于Mindlin解,对盾构机外侧面圆周摩擦力的作用引起的地表竖向变形进行积分得到盾构机外壁与围岩之间的摩擦力引起的地面竖向变形计算公式为

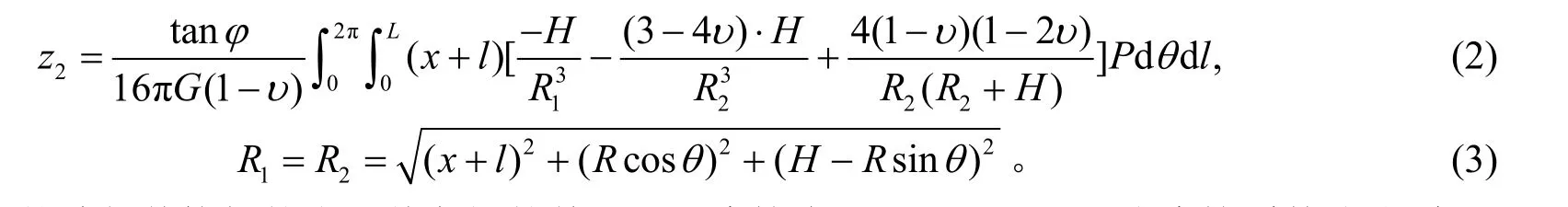
式中：P为盾构机外壁与其接触的岩土体之间的单位面积摩擦力(kPa),P=μFN,μ为摩擦系数(根据本区间地质资料圆砾层摩擦系数取0.5),FN为围岩对盾壳外壁法向压应力,R为盾构机外径,L为盾构机长度。

2.4 盾构施工引起的地表最终竖向变形

将掌子面附加作用应力作用效果和盾壳外壁与围岩土体之间的摩擦力作用效果叠加得到最终隧道轴线上方地表竖向变形。

3 工程实例

本模型工程依托南宁地铁某区间右线典型里程区间,本段区间隧道为两条单洞单线圆形盾构隧道,右线隧道先于左线隧道施工,线间距为14.0 m,覆土埋深15 m。隧道位于⑤1-1圆砾地层,地面高程为76.5 m,地下水位稳定常水位高程为68.29 m。其物理力学参数详见表1。

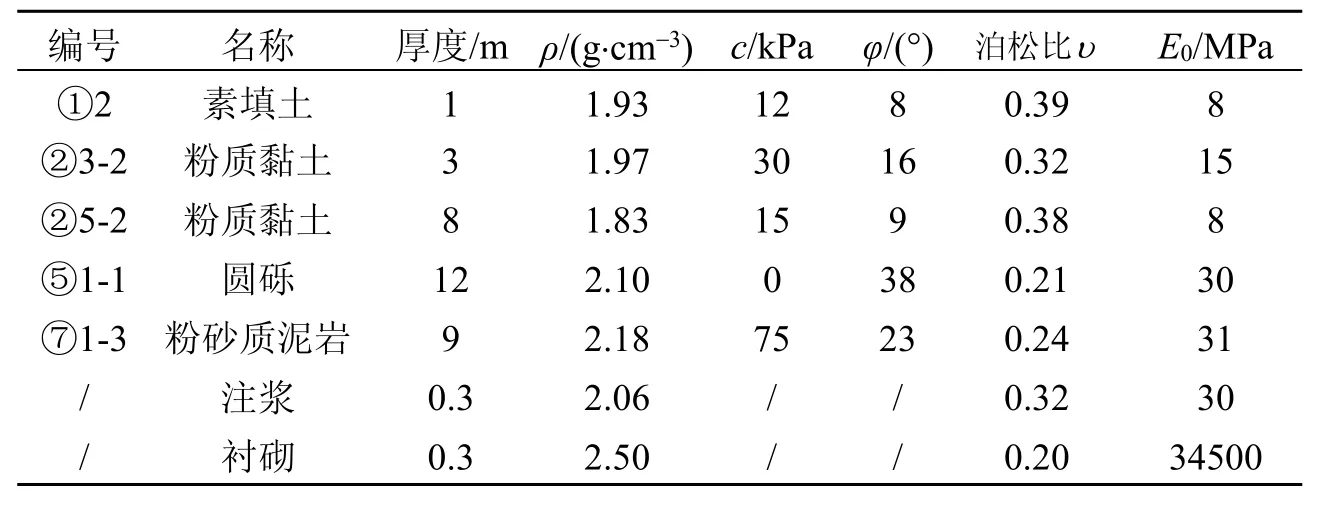
表1 物理力学参数表

3.1 数值分析方法

本文依托南宁地铁某区间右线隧道典型里程地质进行数值分析,隧道盾构施工过程采用FLAC3D软件分析,计算模型选取纵向(Y向)长度60 m,横向(X向)宽度取为56 m,下边界取2倍洞泾即12 m,隧道埋深15 m,即建立长×宽×高(60 m×56 m×33 m)计算模型。盾构机模拟外径为6.24 m,长度7.7 m,隧道外径为6 m,内径为5.4 m,隧道衬砌采用环宽1.5 m,厚度为0.3 m的钢筋砼管片,注浆层厚度取为30 cm。本文地层采用Mohr-Coulomb本构模型,隧道衬砌、壁后同步注浆层采用的则是弹性模型,注浆过程模拟则采用等代层的形式模拟注浆层。数值模拟网络示意图见图2所示。

隧道纵向长度60 m,盾构施工从y=0开始推进,每次开挖4环即6 m,分5步开挖到y=30 m断面,监测得到开挖面前方及后方的地表变形值。具体操作如下：

开挖前,需构建地层的初始应力场。土层在原始自重应力作用下应力达到平衡,然后将土层位移清零,边界约束的速度设为零。

开挖后首先隧道纵向开挖范围0～6 m。开挖模拟为瞬时开挖,掌子面从0 m瞬时达到6 m,并在掌子面施加均布荷载模拟开挖仓压力。在等代层施加均布荷载来模拟盾壳与围岩之间摩擦力。

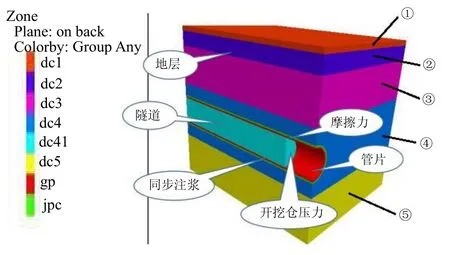
图2 数值模拟网格示意图

重复以上操作,依次进行下一步开挖,直到掌子面开挖到达y=30 m断面。

3.2 盾构施工过程中纵向地表变形计算分析

图3所示为盾构隧道中心线上方的纵向地表变形曲线。由图3可知,盾构隧道开挖过程中,隧道中心线上方纵向地表变形规律基本呈现为“S”型,盾构施工过程中,开挖仓压力会大于或等于掌子面水平土压力,掌子面前方土层还受到来自盾壳与围岩之间向前的摩擦力作用,带动其周围土体颗粒向前移动,应力状态的改变会引起土体的变形,掌子面前方土体受到挤压而隆起,掌子面后方土体存在松散空隙而沉降,随着能量的传播和耗散,掌子面前后方沿着纵向距离方向地表变形量先增加达到某一个波峰而后减小。实测数据、数值分析和理论计算所得数据较吻合,但掌子面后方理论计算所得的沉降量较数值分析和实测数据值小,导致这一原因是理论计算未考虑隧道开挖完成后地层损失及衬砌管片的变形量。

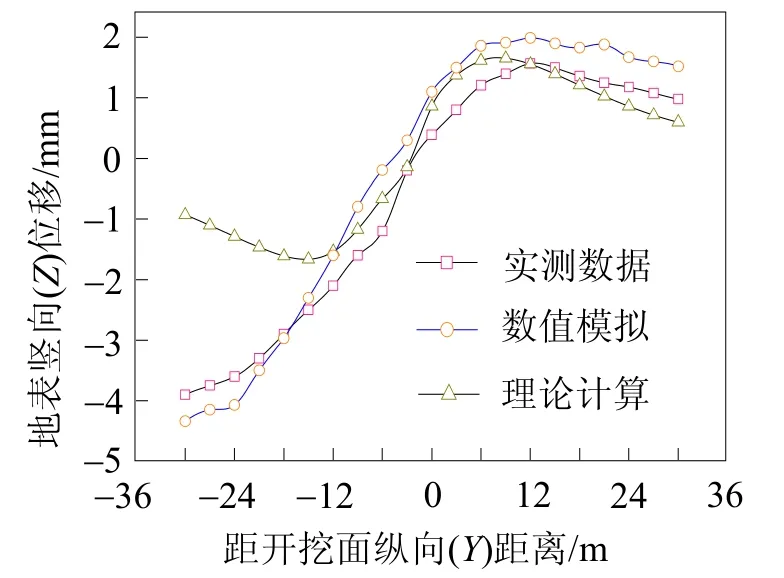
图3 纵向地表变形对比分析图

4 各参数对纵向地表变形敏感性分析

4.1 开挖仓压力对纵向地表变形的影响

盾构施工的一个重要掘进参数在于控制开挖仓压力与隧道掌子面水土压力的平衡。盾构机开挖仓压力是否准确,直接影响着开挖面的稳定和地层的变形。开挖仓压力与朗肯理论计算的掌子面侧向静止土压力的比值,记为RP。本文选取RP=1、1.2、1.4进行对比分析,如图4所示。由图4可知,增加开挖仓压力对地表纵向变形的影响较小,当开挖仓压力增加20%,地表纵向变形增加约5%。地表纵向变形主要还是由盾壳外壁与围岩之间的摩擦力引起。

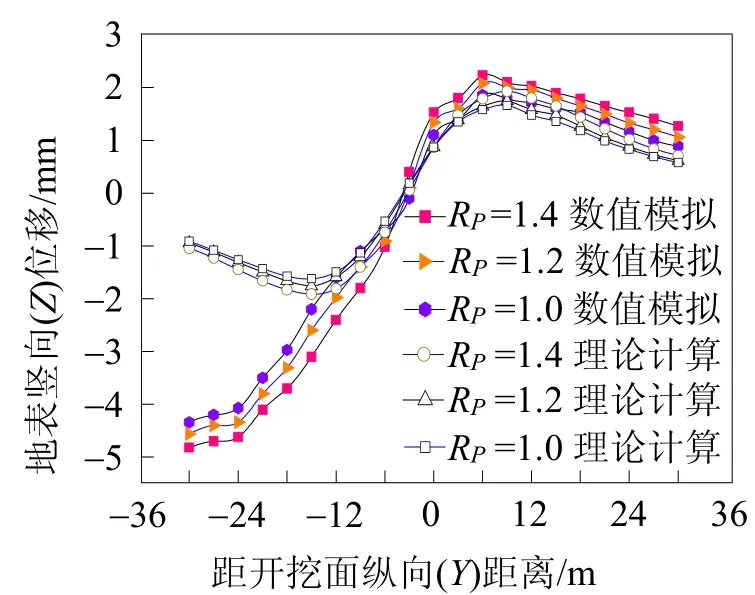
图4 不同RP值纵向地表变形图

4.2 盾壳摩擦力对纵向地表变形的影响

当隧道处于不同的土层时摩擦系数会不一样,根据本区间地质资料,粉细砂层μ为0.4,粉质粘土层μ为0.3,圆砾层μ为0.5,假定在同一埋深盾壳外壁的法向应力一样,从而不同摩擦系数可得到不同的摩擦力。图5所示为不同摩擦系数纵向地表变形曲线。由图5可知,理论计算和数值模拟均可得出盾壳摩擦力与纵向地表变形之间存在着正相关的关系,但并非线性关系,盾构机侧壁与围岩之间形成的摩擦力越大,隧道上方纵向地表变形也越大,盾壳侧壁摩擦力对纵向地表变形影响较大。当摩擦力增加30%,纵向地表变形量增加最大约35%。

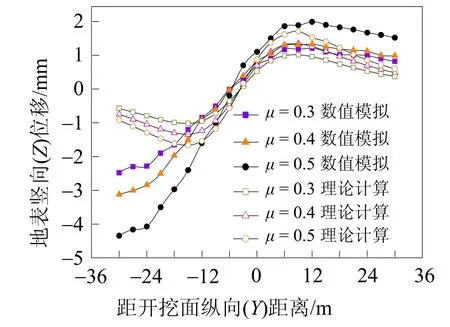
图5 不同摩擦系数纵向地表变形图

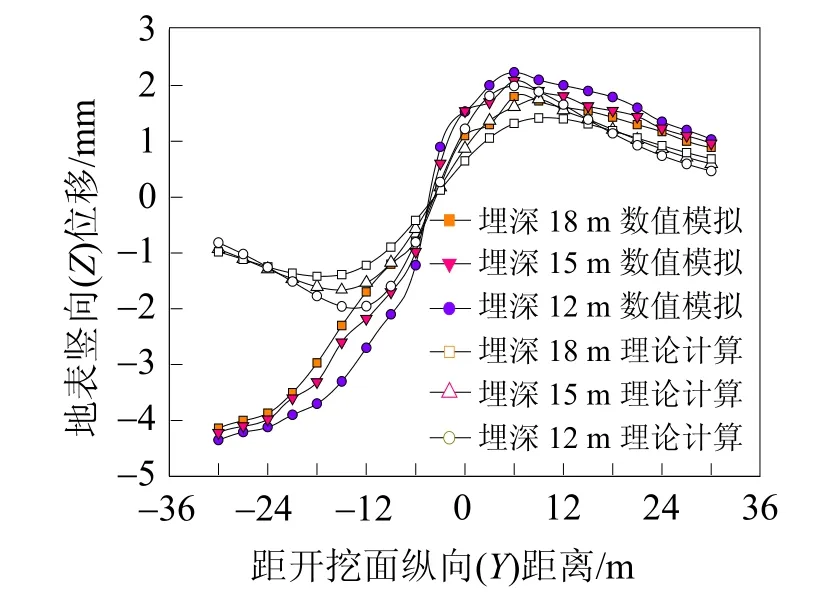
图6 不同埋深纵向地表变形图

4.3 不同埋深对纵向地表变形影响

城市地铁盾构隧道在车站的端头埋深较浅,隧道离开车站后,根据线路的调整,埋深会增加,而在相邻里程范围内地层条件相差不大,隧道埋深的不同,盾构开挖后的围岩应力分布就不一样,纵向地表变形也就不一样。图6所示为不同埋深纵向地表变形图。由图6可知,不同埋深下盾构隧道纵向地表变形规律,同一地层中,隧道埋深的不同,纵向地表变形量也不一样,且隧道的埋深对纵向地表变形量的影响较为显著。在开挖面附近前后25 m范围内纵向地表变形随着隧道埋深减小而增大比较明显,当埋深减小20%,纵向地表变形增加约18%。在掌子面前方超过30 m范围后的纵向地表变形对隧道的埋深的敏感性较小。

4.4 不同变形模量和泊松比对纵向地表变形影响

盾构位于不同地层,其弹性模量和泊松比不同。为了研究弹性参数对纵向地表变形的影响,本文对不同弹性参数展开研究。图7所示为不同变形模量和泊松比纵向地表变形曲线图。由图7可知,随着土层的变形模量减小、泊松比增大,纵向地表变形量增加,当泊松比增加20%,变形模量减小25%,纵向地表变形量增加最大约为50%,土层的变形模量和泊松比的变化对纵向地表变形量的影响较为显著。

4.5 地表变形对土层内摩擦角φ的敏感性

盾构机推进过程将改变隧道周边土层的应力—应变状态,土体的内摩擦角是土的抗剪强度的重要参数,影响着土层的变形量。图8所示为不同内摩擦角纵向地表变形曲线图。由图8可知,随着土体内摩擦角的增大,纵向地表变形也增大,且影响较为显著,但地表纵向变形增加幅度有所减缓;当内摩擦角从15°增加到25°,增量66.7%,纵向地表变形显著增大,增加量最大约为73.1%,当内摩擦角超过25°后,随着内摩擦角的增大,纵向地表变形量也增大,但是增量幅度减小,证明内摩擦角超过25°后,纵向地表变形对内摩擦角的敏感性减弱。

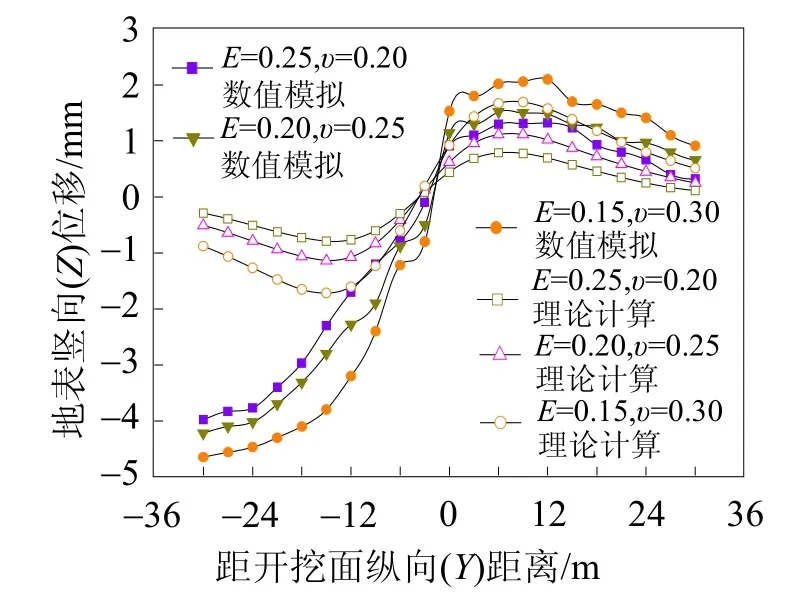
图7 不同变形模量和泊松比纵向地表变形图

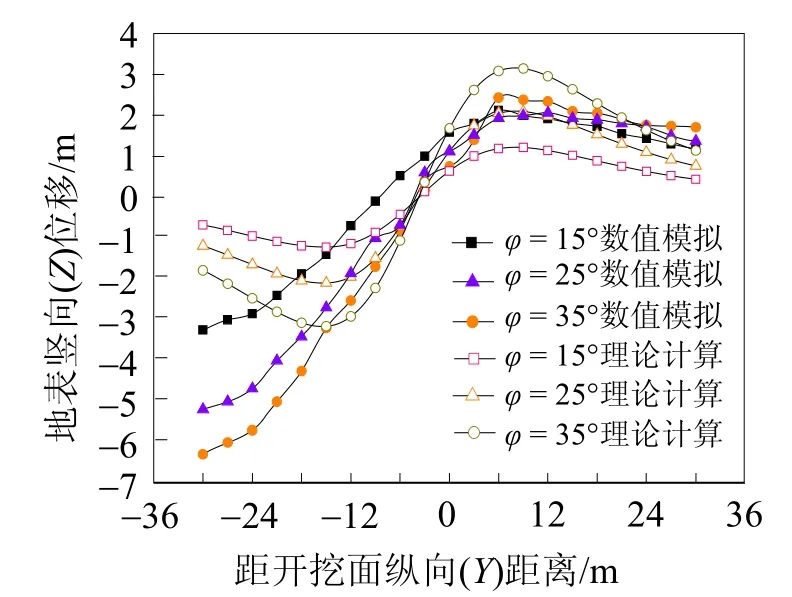
图8 不同内摩擦角纵向地表变形图

5 结论

本文基于Mindlin解,引入摩擦角φ,推导了盾构施工过程中纵向地表变形计算公式,并结合实际工程,与数值分析和监测数据进行对比分析,得到以下结论：

(1)基于Mindlin解,引入了摩擦角,推导了盾构施工纵向地表变形的弹塑性解,与数值分析和实测数据较吻合;

(2)盾构施工过程中,隧道中线上方纵向地表变形规律呈现为S型,掌子面前方地表隆起,掌子面后方地表下沉;

(3)盾壳与围岩之间的摩擦力、土体内摩擦角ϕ与盾构隧道中线上方纵向地表变形存在正相关,盾壳摩擦力增加30%,纵向地表变形量增加最大约35%;内摩擦角增加66.7%,纵向地表变形量最大约为73.1%;当泊松比增加20%,变形模量减小25%,纵向地表变形量增加最大约为50%;开挖仓压力增加20%,纵向地表变形增加约5%;同土层不同埋深,当埋深减小20%,纵向地表变形增加约18%。