基于水利工程模糊指数平滑法的项目造价估算研究

刘庆军

(盘锦市大洼区水利服务中心，辽宁 盘锦 124200)

0 引 言

在可行性研究和项目建议书阶段预测的工程造价即为项目投资估算，它是对近期开发项目作出决策、批准及初步设计的重要依据，且对于保障项目的顺利实施、建设及成本控制具有重要的现实意义。结合以往的实践经验，在我国水利工程项目中超预算决算、超概算预算及超估算概算的“三超”问题较为常见，且在实际工程中通常存在责任人不明确的现象。在项目建设时“三超”问题的出现可产生如下三方面的后果，即建设项目的投入资金显著增大，实际消耗的费用远远高于项目预算；由于无法承担项目预算外的资金负担，建设单位直接进入停滞状态或明显降低项目进度；为保障自然利益和解决建设资金问题，参建单位往往采取降低工程质量的方法，从而导致在后期的服役运行时无法充分发挥其功能作用或埋下安全隐患。总而而言，任何一种不利因素均可对经济建设产生影响并对工程质量和下游区域的安全构成威胁[1-3]。

建设项目出现“三超”问题不仅和自然灾害、设计变更等因素有关，而且受政策变化及市场波动等影响显著，从项目造价管理的角度可认为造价估算针对性差、估算方法不合理、经费到位不及时以及长期采用非标准化设计等综合因素影响，为造成项目造价存在较大偏差的原因。另外，在项目建设初期由于地质勘察难度高、数据资料准确性差等，采用传统的估算方法确定的工程造价往往存在可靠性低、误差大等问题。在日趋激烈的市场竞争下和水利工程快速发展的背景下，亟需建立一套科学有效、适用性强的项目造价估算方法[4-7]。鉴于此，文章将指数平滑法和模糊数学法相耦合，准确、快速的预测分析了建设项目投资状况。

1 建模流程

1.1 相关理论分析

1)指数平滑法。该方法是一种基于时间序列的预测法，其理论依据为移动平滑法，计算公式为：

St=αyt+(1-α)St-1

(1)

式中：yt、St分别为时间t的实际值与平滑值；St-1、α分别为时间t-1的实际值与指数平滑常数，α值处于0-1之间。

实际结果与预测值之间的差异响应速度以及平滑水平和平滑常数α密切相关，确定α值运用该方法的关键。

2)模糊数学法。基于模糊集合论的模糊数学式客观世界中的模糊性与经典数学之间的桥梁，而模糊集合是由Zadeh提出的用于描述事物模糊性特征的方法。在模糊集合中模糊度、贴进度这两个概念至关重要，为表征两个模糊集合的相似程度王培庄教授提出了贴进度的概念及其计算公式。

1.2 估算模型的构建

文章结合模糊数学相关方法和指数平滑法理论依据，构建了用于估算预测工程投资的数学模型，其主要流程如下：

1)设已建水利项目有n个，将其标记为A1，A2，…，Ai，i=1,2，…，n。项目的特征元素采用集合T表示，已建项目的特征元素有m个，由此可将集合T计为T={t1,t2,…,tj}，j=1,2，…，m。

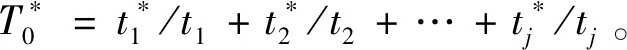
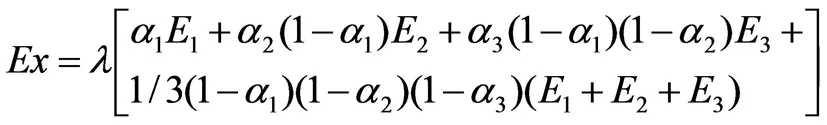
(2)

式中：λ、Ex分别为调整系数与工程项目的预测投资；E1、E2、E3分别代表已建项目的投资估算值；α1、α2、α3为排序为1、2、3名项目的贴进度，且满足α1≥α2≥α3。

选择平滑常数作为贴进度α，拟建项目与典型项目的相似程度随着贴进度的增大而增大，即贴进度越大则水利工程的投资估算的精度越高，对于投资估算值的变化特征可引进预测值的大小来反映。

2 模型参数的确定

2.1 选取相似工程项目

结合水利项目对地点的依赖性及其自身的多样性、复杂性、单体性等特征，在造价估算与风险管理过程中存在着各种各样的不确定因素和复杂多变的环境条件，如坝体裂缝、坝基失稳以及水库滑坡等。对于总体上相似的工程项目往往难以在国内外已建项目中选取，且各项目之间的整体可比性较差，如果能够与其他类似或同类项目相比拟建项目所拆分的分部分项工程具有较强的可比性[8]。因此，文章从系统论的角度将整体水利工程分解为若干个子项目，例如将大型水利枢纽工程分解为船闸、电站、泄洪洞、尾水洞、引水洞、溢流堰及拦河坝等子项目。对于分解后的拟建工程各子项目，在许多已建工程中很容易确定具有较高类似程度的项目。

2.2 确定特征元素

工程造价涉及到的范围广、因素多且计算过程较为复杂，任意一项参数的改变均可对工程造价产生一定的影响和波动，且不同特征元素的影响程度存在一定差异，如果全部考虑、统一对待各特征元素并忽略其间的差异影响，则造价估算结果势必会产生偏差。为便于计算并确保估算结果的可靠性，一般情况下将工程特征元素确定为影响造价的主要因子，然后将其集合起来构成能够反映特征项目的特征元素序列。结合工程实践和相关资料，对水利工程选取能够显著影响项目造价的特征元素如下：

R=[R1，R2，R3，R4，R5，R6，R7]=
[地质条件，水文条件，坝型，
最大坝高，坝长，装机容量，工期]

为提高预测结果的可靠性，列举了水利工程发电厂房、拦河坝、引水及泄水建筑物等子项目的特征元素见表1。

表1 水利工程子项目特征元素集合

2.3 计算隶属度和贴进度

1)隶属度的计算。依据经验或统计数据确定的隶属函数值具有较强的主观性，在模糊集合计算时应遵循的原则为：工程项目特征元素的隶属度与工期、造价、资源耗量、施工难度以及结构复杂程度密切相关，二者呈正相关性。目前，主要有如下两种方法确定隶属度tij，即：采用线性插值法确定坝高、坝长等能够定量反映项目特征元素的隶属度值；根据级别划分状况确定能够定性反映项目特征元素的隶属度，如根据相关资料将岩石划分为8个级别，结合实际情况赋予不同的隶属度，隶属度越趋近于1代表岩石的级别越高；根据不同的方式将断面型式、之衬方式、开发方式等赋予不同的隶属度。

2)贴进度的计算。对于贴进度的计算可定量反映估算对象的相似程度，相似程度与贴进度呈正相关性，即相似度越大则贴进度越大。结合模糊数学相关法则，通过如下推导确定贴进度计算公式：

设拟建水利项目和第i个已建工程项目的隶属函数值分别为A={a1，a2,…,qm}、Bi={bi1,bi2,…,bim}，将二者进行内积运算有：

A⊗Bi=(ai∧bi1)∨(a2∧bi2)
∨…∨(am∧bim)

(3)

外积：

A⊕Bi=(ai∨bi1)∧(a2∨bi2)
∧…∧(am∨bim)

(4)

采用下式计算确定二者贴进度，即：

(A，Bi)=1/2[A⊗Bi+(1-A⊕Bi)]

(5)

式中：∧、∨分别代表取最小和取最大值。

2.4 求解调整系数

对调整系数λ值按照经验公式计算确定，即：

λ=1+1/m[1.8×(T′/Tα1-1)+0.8×
(T′/Tα2-1)+0.4×(T′/Tα3-1)]

(6)

式中：m为水利工程投资估算的项目个数；T′为拟建项目的模糊系数，即所有项目隶属度之和最大值∑tmax中拟建项目隶属度之和∑t′的占比；Tα1、Tα2、Tα3为α1、α2、α3对应项目的模糊系数，即所有项目隶属度之和最大值∑tmax中与其隶属度之和∑tij的占比。

3 投资估算模型的验证

3.1 数据资料

辽宁省盘锦市某待建水电站项目F为混凝土重力坝，高150m、长640m，电站总装机设计容量260万kW，年发电量115.28亿kW·h，总库容9.12亿m3，动态投资和静态投资分别为148.72、125.04亿元。根据文中所述方法将该水电站待建项目划分为多个子项目，采用模糊指数平滑法估算坝基帷幕灌浆子项目投资，选择5个近期已建类似项目A、B、C、D、E进行计算，结合子项目施工特点将其分解为灌浆方法、平均孔深、孔径、孔距、孔斜以及地质条件6个元素，各特征元素的贴进度计算结果见表2。

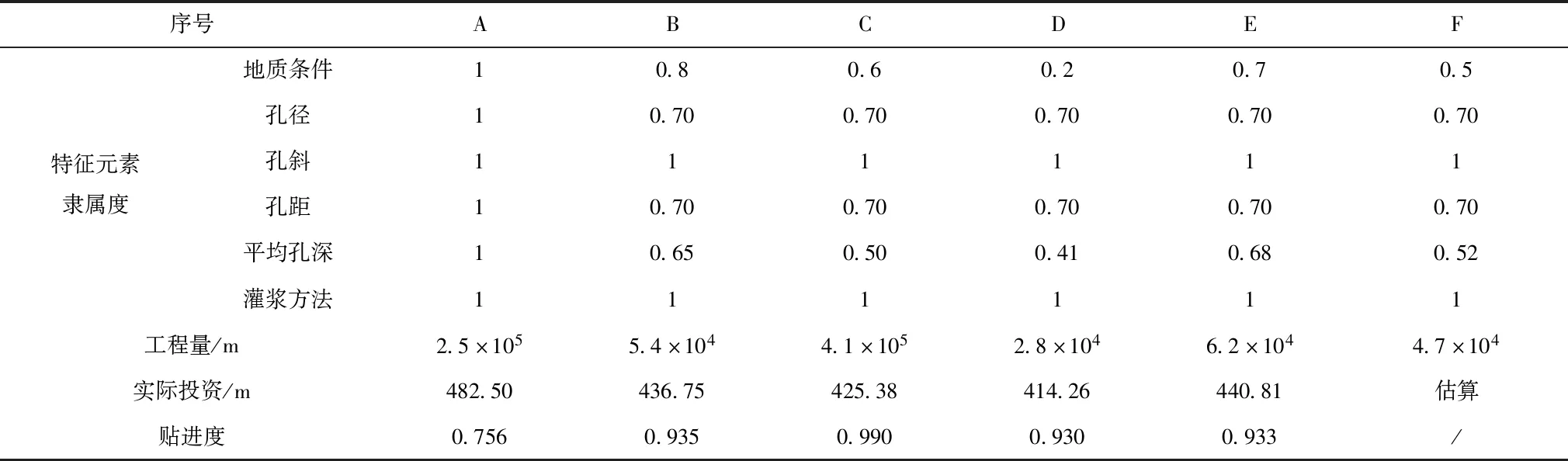
表2 坝基帷幕灌浆子项目贴进度计算结果

3.2 结果分析

对A-F项目的特征元素隶属度函数值tij按照文中所述隶属函数值计算方法确定，计算结果见表2所示，具体流程为：

1)根据表2各特征元素的隶属度计算结果tij，确定A-F项目的函数值代数和∑tij，即：∑tAj-∑tFj分别为6、4.85、4.50、4.01、4.78、4.42，其中j=1,2,…,6。由于代数和最大值为A工程项目，结合模糊系数计算公式可确定TA=1、TA-TF分别为0.81、0.75、0.67、0.80、0.74。

2)对已建项目A、B、C、D、E与待建水电站项目F的贴进度利用公式(5)计算确定，即(F，B)-(F，E)的贴进度依次为0.756、0.935、0.990、0.938、0.931，按照由大到小原则将贴进度进行排序为：α1=0.990、α2=0.935、α1=0.933，相应的投资估算分别为425.38、436.75、440.81元/m。

3)采用公式(6)确定调整系数λ值为1，利用公式(2)计算该水电站待建项目F的估算投资为425.81元/m。根据该工程可行性研究报告和相关数据资料其投资估算值为416.20元/m，通过得到估算误差为0.02满足不大于0.05的精度要求，因此在估算工程投资方面模糊指数平滑法具有较高的可靠性与可行性。

统一时间为估算工程投资的重要条件，所以在实际估算时应结合不同地区的差异系数适当调整一些重要数据，相关参数可从官方网站提取，考虑到文章篇幅限制不再赘述差异系数的提取过程。

4 结 论

科学合理的估算工程不仅有利于建设项目造价风险因素的控制，而且可为实现水利项目预期的成本目标、质量目标提供重要的依据。文章将模糊数学法和指数平滑法相耦合建立一种预测精度高、计算速度快的构成投资估算方法，该方法具有如下特点：在设计图纸尚不完善的条件下无需借用投资估算指标和分布分项工程量计算，即可快速、准确的确定项目投资，可为水利工程投资风险控制及项目的启动决策提供一定指导。另外，在运用该方法时需要参考其他相似项目的造价数据，因此建立完整的造价数据库为未来发展趋势。