复杂网络下基于路径选择的表示学习方法
2020-04-24刘琼昕龙航郑培雄
刘琼昕, 龙航, 郑培雄
(1.北京市海量语言信息处理与云计算应用工程技术研究中心,北京 100081;2.北京理工大学 计算机学院,北京 100081;3. 哈尔滨工程大学 计算机学院,黑龙江,哈尔滨 150001)
目前业内已经累积了很多大型知识图谱knowledge bases(KBs),如Freebase,DBpedia和YAGO,这些KBs由大量三元组构成,知识图谱中的节点代表实体,节点之间的连线代表关系,每一个三元组描述一个事实,如(Paris,capital-of, France). 在知识图谱构建过程中,存在着知识补全问题. 虽然一个普通的知识图谱就存在数百万的实体和数亿的关系,但相距完整还差很远. 知识推理是利用现有知识图谱中的信息对缺失部分进行补全.
在知识推理领域中,经典的基于路径推理是路径排序算法[1](path ranking algorithm,PRA),由Lao&Cohen于2010年提出. PRA算法可以看作是沿一组带有关系信息的边上的随机游走算法,它与经典随机游走算法RWR[2]相比,主要优势在于它加入了限制游走的边的类型信息. 原始的PRA算法的主要思想是将关系对应的路径集合抽取出来作为推理的特征集合,游走概率作为特征值,然后构建分类器训练出每条路径对应的权值,作为推理的依据. 针对PRA算法的特征集规模巨大,耗时长等问题,相继提出了一些改进算法[3-5]. 其中有借鉴性的思想是在抽取路径特征集合时使用双端广搜的方式,对于三元组头尾同时进行搜索,根据搜索交点拼接为最终路径. 另外在众多的改进算法的实验过程中,人们发现使用二值更适合作为路径特征值,可以节省计算游走概率时的计算开销.
另一个知识推理的经典算法是基于知识表示的TransE[6]算法,由Bordes于2013年提出,它假设存在隐式的向量空间,将知识图谱中的实体和关系在低维的空间里进行表达,得到连续的向量. 将两个实体之间抽象的关系映射为两个向量之间的转换关系. 正式的表示:对于任意三元组(h,r,t),实体h和t嵌入到向量h和t,关系r嵌入到向量r都存在h+r≈t. TransE算法在推理方面表现良好,实现简单,但是对于一对多、多对一、多对多关系有着很大的缺陷. 后续提出的算法如TransH[7]和TransR[8]针对TransE模型的缺陷进行了改进,取得了较好的效果.
当前新的研究方向是将知识表示和路径推理算法相结合[9-10],例如PTransE算法,基于TransE的基本假设,将路径像实体和关系一样在低维向量空间表示出来. 对于任意三元组(h,r,t) 头尾实体之间的一条路径p=[r1r2…rl] ,都存在路径向量p=r1∘r2∘…rl,运算符∘是向量之间的运算方式,作者尝试了相加、相乘、RNN循环神经网络3种结合方式. 通过将路径向量化,可以将路径作为约束加入到最终的得分函数中. 模型推理效果较之前有很大的提升,由于加入了路径的约束,模型在一对多和多对多关系的表现上也十分突出.
但是PTransE的模型中对路径信息的处理略显简单,导致路径特征空间十分庞大,其中包含着大量冗余路径,冗余路径会降低模型的泛化能力,影响推理准确性. 而且模型忽略了对缺失路径信息三元组的处理. 针对上述问题本文提出了一种基于路径选择的表示学习方法,通过机器学习算法对路径进行选择,将得到的关键路径特征用于最终的知识表示学习. 实验证明,本文提出的模型可以提高推理准确率,提升效率.
1 问题描述
对本文用到的符号和需要解决的问题进行了描述与定义.
对于一个知识图谱T=〈E,R,S〉,实体集合E,关系集合R,任意三元组(h,r,t)∈S,三元组头尾h,t∈E,关系r∈R. 任意关系r的存在路径特征集合Πr=(p1;p2,…;pd),Πr是所有存在关系r的实体对间路径集合的并集,Πr中路径对应权值为路径置信度w=[w0w2…wd].
在某种程度上路径特征可以视作是推理关系r的证据和现象,本文将路径特征主要分为3种类型.
定义1强证据Sr(p),弱证据Wr(p),伴随现象Cr(p),
Πr=Sr(p)∪Wr(p)∪Cr(p),d=k+m+o.
① 强证据:具有较高的置信度的路径集合.Sr(p)={p1,p2,…,pk},k=|Sr|.
② 弱证据:具有较低的置信度的路径集合.Wr(p)={p1,p2,…,pm},m=|Wr|.
③ 伴随现象:由于对于关系r来说有很大一部分路径是事实出现的伴随现象,这些路径如果作为证据出现会对推理造成负面作用,所以伴随现象不能作为推理关系的证据.
Cr(p)={p1,p2…,po},o=|Cr|.
在分类过程中通过训练路径的置信度来处理3种不同情况. 对实体间路径特征进行进一步的分析,有以下几个关键问题需要解决.
问题1特征冗余问题,以FB15K数据集为例,单单founders关系就有上千条路径(两步游走)而这上千条路径中对于目标关系来说不是全部都有用的,需要对路径特征进行筛选. 根据它们对推理的作用上文已经分为3种类型,需要将非证据路径尽可能筛选掉.
问题2特征相关问题,对于大部分关系而言,路径特征之间不是相互独立的,会存在相互依赖的多重特征. 路径作为证据出现的模式往往不是单独一条路径,而是由相关路径共同组成的证据. 所以简单的线性模型不能很好地处理特征的相关性.
问题3样本缺失问题,对FB15K中的三元组统计,某些关系虽然存在着大规模的路径特征空间Πr,但是存在此关系的样本数量n却很少,会出现d>n甚至d≫n的情况. 另外知识图谱中只能采样得到正确三元组,所以会导致负样本缺失的问题.
2 模型描述
在这部分将详细的介绍本文基于路径选择的表示学习模型(knowledge embedding based on path feature extraction KEPE). 模型主要分为两个部分:第一部分是路径选择模块,主要是进行关键的路径的筛选,以及对应路径置信度的计算;第二部分是表示学习模块,主要功能是结合关键路径信息构建知识表示模型,学习得到实体关系向量. 具体模型各模块内部结构和交互方式如图1所示.
2.1 路径选择模块
2.1.1路径特征抽取
路径特征抽取过程与PRA算法类似,在头尾实体之间进行随机游走或者深度优先搜索,获取每一对三元组实体之间的路径集合. 因为需要对图谱中每一个关系建立分类器,所以需要统计所有存在关系r的实体对作为样本,并取所有样本的路径集合的并集作为关系r的特征集合Πr=(p1;p2,…;pd).
2.1.2特征值计算
原始PRA算法采用游走概率作为特征值,在知识图谱中两个节点之间的路径数量会很大,对推理有很强的置信度的路径可能游走到的概率并不是很高,所以置信度的和路径游走概率没有很密切的相关性. 并且在多篇相关文献中实验证明[11],使用随机游走概率对于推理效果没有明显的提高.
另外在计算关系路径概率时时间开销过大,在构建概率特征空间时,需要遍历所有样本和样本路径,并且在计算路径特征值时要计算路径的每一跳的游走概率,假设样本数量为N,样本对应路径期望个数为P,路径长度为L,每一跳游走概率的计算开销K,综上的构建特征空间的时间复杂度为O(NPLK). 而在构造二值特征空间的过程中,只需要遍历所有样本和样本的路径集合,构建特征空间的时间复杂度为O(NP). 所以为了提高算法的效率决定采用二值化的特征空间,放弃原始算法的游走概率特征值,在本文的实验部分对两种不同特征值方法的时间开销和效果进行了对比说明.
2.1.3置信度计算
针对第1节中提出的问题,本文构造了基于学习算法的路径特征选择模型.
在建立模型之前,首先需要解决负样本缺失的问题,本文提出一种构造负样本的方法:对于某一目标关系r,随机在其他关系中随机选择其中一个样本,如果该样本的两个实体之间不存在目标关系r,则将该样本作为负样本. 正负样本个数比例为1∶1.
① 线性模型:特征冗余问题可以通过将非证据路径的置信度置为0来解决,对于线性模型而言,使用L1范式对参数进行正则化可以得到稀疏的参数向量,去除伴随现象和部分弱证据. 由于样本的缺失,可能会导致训练出来的置信度会和实际作用有所差别,置信度的偏差会导致后续推理的严重偏差,所以希望可以得到稳定的参数,使得模型具有一定的容错性,出于这方面考虑在使用L1范式基础上再使用L2范式进一步对线性模型进行正则化,L2范式可以有效缓解ill-condition的情况从而得到稳定的参数. 综上所述,本文采用基于弹性网络(elastic net)[12]的线性模型进行特征选择,elastic net可以很好地处理多重特征的情况,对于多路径间的相互依赖,Lasso倾向于随机的取出其中一项,而弹性网络则倾向于成组的来取出. 正式定义目标函数为

(1)
目标函数中的超参数α和ρ,α为控制正则化惩罚力度的参数,ρ为 控制L1,L2范式所占比重的参数. 在超参数集上进行交叉验证,确定优选参数. 通过梯度下降更新权值w,最终得到w=[w1w2…wd]作为特征空间Πr=(p1;p2,…;pd)中各路径的置信度.
② 非线性模型:由于路径特征之间未知的相关性,为了得到可以处理非线性关系的模型,本文决定采用基于决策树的集成学习模型,弱学习器之间采用bagging的方式进行结合,也就是随机森林算法[13](random forest). 使用随机森林算法本文可以得到最优的前m路径,并且利用随机森林对多元共线性不敏感的特性使模型在缺失样本和特征相关的情况下依旧保证良好的效果. 另外模型对在特征的选择和样本的使用上进行随机化,可以使模型具有很强的泛化能力.
本文采用袋外误差为依据进行特征选取. 如算法1所示.
算法1:关键路径选取
输入:特征空间Πr=(p1;…;pd),样本集合,决策树数量n,关键特征数量m.
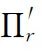
1. loop
2.利用特征空间Πr建立包含n颗决策树的随机森林.
3.计算每颗树的袋外误差,第i颗树i=1,2,…,n的袋外误差为errOOB(i).
4. forpj∈Πrdo
5.计算特征pj的重要性. 随机地对袋外数据OOB所有样本的特征pj加入噪声干扰,计算袋外误差errOOB′(i).
6.计算特征X的重要性:
7. end for
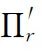
9. end loop直至选出m个特征.
2.2 表示学习模块
本模块延用TransE的实体和关系向量化方法以及TransE的目标函数,保证头、尾和关系之间的联系. 在此基础上,使用路径信息进一步对模型进行优化.
2.2.1构造负例
对于任意三元组来说,随机替换其头,尾,关系得到不出现在数据集中的三元组数据集合为
S-={(h′,r,t)}∪{(h,r′,t)}∪{(h,r,t′)}.
对关系损失函数来说,要分别替换头尾,关系作为负例,对于路径损失函数来说只需要对关系进行替换.
2.2.2优化目标函数
目标函数主要分为两个部分,一部分是实体之间关系约束,另一部分是实体之间的路径约束[14].
正式的表示,对于长度为l的路径p=[r1r2…rl],路径向量由关系路径中的关系向量的相加得到,表示如下p=r1+…+rl,对于一个三元组(h,r,t),能量函数的定义如下:E(h,r,t)= ‖h+r-t‖,来确保r≈t-h成立. 对于一个路径三元组(h,p,t)来说,能量函数定义如下:E(h,p,t)= ‖p-(t-h) ‖=‖p-r‖=E(r,p). 路径p作为推理关系r的有效规则之一,需要保证能量函数E(r,p)可以得到尽可能低的分数.
综上所述,本文确定模型目标函数如下.
(2)
等式右边L(h,r,t)是对实体关系的约束,L(p,r)是路径关系约束,R(p,r)是上文通过路径特征选取算法得到的路径p对于推理出关系r的置信度,是路径置信度w中的非零项,P(h,t)是实体对之间所有路径的集合. 等式右边最后一项是目标函数的正则化项,λ是正则化项的超参数,Θ={h,t∈E}∪{r∈R}.
目标函数使用hinge损失函数,得到目标函数进一步表示为
L(h,r,t)=
(3)
L(p,r)=
(4)
采用批量梯度下降[15-16]的方式对目标函数L(S)进行最小化,迭代直至收敛,最终得到关系和实体的向量.
3 实验结果与分析
实验主要针对知识库补全的两个方面,实体预测和关系预测. 另外实验还会展现路径选择得到关键路径的有效性.
3.1 数据集和实验设置
为了检验本文提出的方法,本文在公开数据集FB15K上将本文的方法和知识推理领域的代表性算法进行对比实验. FB15K来自Freebase[17],Freebase是关于世界的一般知识(来源维基百科). FB15k数据集是Freebase的一个子集,包含14 951个实体,1 345个关系类型和592 213个三元组,数据集信息见表1.

表1 数据集
3.2 关键路径选取
路径选取模块通过学习路径置信度来获取关键路径,在该模块中本文分别采用两种分类器来对路径进行选择,采用不同的验证方式来调节参数,检验选取效果.
① 弹性网络模型:确定一组备选参数后采用K次交叉验证[18]的方法. 最终得到优选参数,经过弹性网络选取得到备选路径集合.
② 随机森林模型:确定一组备选参数后,利用袋外数据误差来对特征的重要性进行度量,这已经经过证明是无偏估计的. 最终得到备选路径集合.
路径筛选后,以弹性网络模型为例,本文随机选取部分关系对应的关键路径特征top3如下所示,图中关系前的~符号代表逆关系,对三元组(h,r,t)调换头尾形成的三元组为(t,~r,h),关系~r是关系r的逆关系. 表2为关键路径选取结果,以championships关系为例,路径1表明如果某人获得某项比赛冠军,那他首先要参加(tournament)比赛;路径2表明某人属于某个队伍,该队伍是比赛的获奖者,那此人很有可能是冠军;路径3和路径2类似,关键路径符合推理逻辑.

表2 关键路径
3.3 知识库补全
知识库补全是本文要解决的主要任务,当前知识库存在大量缺失的三元组,对三元组(h,r,t)来说实体和关系都可能作为缺失的部分出现,为了推理出缺失的部分,本文利用KEPE模型得到的实体和关系向量来完成知识库补全任务.
在测试阶段,已知三元组其中的两部分,来对第三部分进行预测. 对三元组(h,r,t)定义如下打分函数来计算候选项的得分. 函数(5)定义如下:
Score(h,r,t)=G(h,r,t)+G(t,r-1,h).
(5)
G(h,r,t)包含两部分:一部分是关系损失;一部分是路径损失. 综合两部分损失越低,该备选三元组越有可能成为最终预测结果. 最终得到G(h,r,t)定义为
G(h,r,t)=‖h+r-t‖+
(6)
考虑到当一对实体之间除了关系r以外不存在任何路径,那么三元组路径损失为0,但是对于存在路径的三元组来说,损失是恒大于0的. 路径的存在理应是对推理起到推动作用的,所以定义θ为没有路径信息三元组的惩罚项,作为一个协调关系和路径损失的参数. 改进后的G(h,r,t)式(7)定义如下:(在下文中使用式(7)作为打分函数的模型使用bp符号来进行区分)
G(h,r,t)=‖h+r-t‖+
(7)
3.3.1实体预测
本文将候选实体填补后得到的候选三元组的G(h,r,t)由低到高排列. 排列靠前的作为预测结果. 本文使用两种方式Hit@N和MeanRank对模型的效果进行评判. 对比实验包括经典的表示学习算法RESCAL[19],SE,SME[20],本文模型基于的TransE和PRA算法,Trans系列的改进算法TransH,TransR,以及路径与表示学习的融合算法PTransE.
① Hit@N指标是对候选三元组进行排序后得到的序列取前N个,Hit@N是这N个三元组命中为正确三元组的概率.
② MeanRank指标是指正确三元组在序列中的平均排名.
将只在测试集上进行模型的测试记为“Raw”,将在整个数据集中测试称为“Filter”.
在实验过程中,本文对上述的所有参数在验证集上进行了选择. 包括梯度下降的学习率α、批量b向量维度d、hinge损失函数的γ、协调参数θ. 在验证集上进行参数调节之后,得到如下参数取值:α=0.001,b=100,d=100,γ=1,θ=1.7,训练迭代次数为500次.
如表3,KEPE_EN是采用弹性网络进行路径选取的模型,KEPE_EN_R 为使用随机游走特征空间的弹性网络模型,KEPE_RF为采用随机森林进行路径选取的模型. 括号中第一项为测试阶段是否采用平衡因子,第二项为路径长度. 本文模型的各项指标在整体上明显优于Baseline. 与同为路径和知识表示结合模型的PTransE的实验效果相比,本文模型优势也十分明显. 下面将对比PTransE模型对实验的各个方面进行分析.

表3 实体预测结果
由表3可见,PTransE路径长度为3时除了Filter指标略有提升以外,其他指标都是下降的,另外当路径长度为3时路径特征空间已经达到一个不可接受的规模. Filter指标Raw指标没有同时提升,模型极有可能已经过拟合. 经过实验表明路径长度为2已经可以获取足够的路径信息.
KEPE模型相比PTransE有着更好的泛化能力,在计算Filter指标时由于预测正确训练集中的三元组也要算入准确率,所以当模型过拟合时Filter指标会异常好,而Raw指标一般会表现变差. 本文提出的模型在同时在两种指标下的表现都很优秀,表中Raw指标和Filter指标相比PTransE模型都有着7%左右的提高,而且使用平衡因子的模型Hits@10的准确率已经达到了90%.
KEPE_EN_R和KEPE_EN的实验数据对比,说明在特征空间的采用上,二值空间和游走概率空间有着相似的效果,而在构建特征空间的时间消耗上,前者要比后者节省1/2以上的时间,所以本文后续实验都采用二值化的特征空间.
KEPE_EN和KEPE_RF是作者采用线性和非线性两种方式对路径进行选取生成的不同模型,模型表现没有太大区别,但是普遍高于对比实验,说明两种模型都很好的解决了样本数量少,特征空间冗余,特征相关问题.
加入了平衡因子bp的模型共性是在Hit@10这项指标上表现更好,而在MeanRank这项指标上表现稍差,参照表3针对这种现象进行分析,平衡因子的加入可以将路径缺失的候选三元组获得较低的评分,但是当这些三元组确实存在数据集中,实际上排名会很靠后,所以导致整体MeanRank会偏大,但是从命中率上看,很多情况下这些缺失路径信息的候选三元组并不是最终的正确的结果,所以添加平衡因子综合考虑下是很有必要的. 如表4所示对比TransH和TransR模型,本文提出的模型通过结合路径信息进一步提升了一对多,多对一和多对多关系类型的预测效果,尤其是在预测头的多对一关系类型时.

表4 实体预测各关系类型的结果
3.3.2关系预测
关系预测是指给定三元组中的头和尾,利用图谱中的信息来对实体之间存在的关系进行推理,由于实验中关系预测的Hit@10指标已经达到了将近100%,所以这里本文采用Hit@1指标来对实验结果进行评判. 如表5所示MeanRank指标与PTransE相比没有明显变化,但是在Raw的Hit@1指标上本文提出的模型表现突出,进一步证明本文的模型在关系预测上也有很强的泛化能力.

表5 关系预测结果
4 结 论
本文提出的复杂网络下基于路径选择的表示学习方法,结合了路径推理算法和表示学习方法的优点,提高了模型整体的推理能力. 在路径选择阶段进行关键路径选择,精简了路径特征空间,缩短了训练时间,进一步提高了模型的泛化能力. 另外在模型测试过程中添加的平衡因子对缺失路径信息的三元组进行了处理. 虽然在路径选取阶段本文进行了优化处理,但是本文没有考虑到关系间存在的联系[21],未来工作将进一步挖掘相似关系之间的联系,运用在路径选择上.
