基于虾螯结构的仿生薄壁管吸能特性分析及优化
2020-04-24黄晗许述财杜雯菁邹猛宋家锋张金换
黄晗, 许述财, 杜雯菁, 邹猛, 宋家锋, 张金换
(1.南京航空航天大学 航空学院,江苏,南京 210016; 2.清华大学 汽车安全与节能国家重点实验室,北京 100084;3.吉林大学 工程仿生教育部重点实验室,吉林,长春 130022)
吸能元件主要有金属薄壁管、复合材料管、泡沫材料、蜂窝材料和点阵材料等[1-4]. 其中,金属薄壁管具有强度高、成本低、吸能效率好等优点,广泛应用于汽车、航空航天领域[5]. 近年来,随着工程仿生技术迅速发展[6],国内外学者采用结构仿生原理对薄壁管进行研究. 文献[7-8]中通过对楔叶类径杆截面结构的观察,设计了一种仿生双层薄壁管复合结构,通过有限元仿真,分析了晶胞单元数、内管直径和壁厚对薄壁管耐撞性影响,并通过多目标优化方法获得薄壁管最优结构尺寸,该研究为提高薄壁管的耐撞性,以及汽车的数值结构分析与优化设计提供了理论基础. 许述财等[9]基于竹结构设计出由仿生节、仿生单元和仿生内管组成的仿生吸能管,并利用有限元法模拟了仿生吸能管的轴向碰撞吸能,利用响应面法求得了仿生吸能管的最优结构. 通过相似性分析,选择牛角作为生物原型,提取出决定牛角耐撞性能的结构特征参数,设计出一种具有牛角结构特征的仿生薄壁管,仿真结果表明该仿牛角薄壁管结构比吸能比普通锥管的提高了1.8倍.
文中将以一种雀尾螳螂虾为仿生原型,结合其螯结构耐撞吸能特性,采用结构仿生学原理,设计出一种具有虾螯结构仿生晶胞单元的薄壁管,对其轴向和径向吸能特性进行了有限元仿真分析,采用响应面优化方法进行多目标优化,获取仿生薄壁管最优结构尺寸.
1 仿生薄壁管仿真分析
1.1 仿生原型分析
雀尾螳螂虾为肉食性节肢动物门口足目,体长最大可达18 cm,其掠肢经过数千万年的演化,已经进化成“锤”状螯(图1),能轻易砸开甲壳类、贝类、螺类等动物的硬壳,甚至能敲碎玻璃鱼缸,持续敲击超过5万次螯才会损坏. 试验表明,虾螯能够承受
超过700 N的瞬时冲击力,最大冲击速度和加速度分别达到23 m/s和1.02×105 m/s2. 研究结果表明,虾螯能够承受较高强度的冲击,并能够通过自身结构吸收冲击能量,呈现出优异的高强、止裂、耐冲击等特性.
雀尾螳螂虾在敲击猎物时,螯前端为直接接触区域,冲击载荷由前端经软组织传递至后端. 试验发现,虾螯结构承受冲击载荷过程中,出现两次峰值载荷,第一次峰值载荷出现在刚接触猎物时,载荷传递至虾螯中部时出现第二次峰值载荷,第二次峰值载荷值约为第一次峰值载荷的1/2. 由此可见,虾螯通过逐级缓冲达到吸能的效果. 另外,虾螯中腔体的存在,使得承受外界载荷时其两侧易于变形,同样达到缓冲吸能的作用.
虾螯与薄壁管在功能和载荷方面具有以下相似性:
① 功能相似性:薄壁管能够依靠自身的溃缩变形来吸收碰撞能量,从而避免整体结构的破坏. 同样,虾螯可以通过其在冲击过程中吸收能量来达到自我保护的目的.
② 载荷相似性:在汽车碰撞过程中,为了保护整体结构,薄壁吸能管要承受来自不同方向的撞击载荷. 雀尾螳螂在捕食过程中,虾螯也要承受来自不同方向的外界载荷.
因此,选取雀尾螳螂虾螯为仿生原型,通过结构仿生原理进行薄壁吸能管的仿生设计,可为薄壁管优化设计提供新思路和参考.
1.2 仿生薄壁管模型
考虑到工程应用、加工精度和成本控制等,基于虾螯结构实际尺寸的3倍进行等比例放大,将其应用到仿生晶胞单元设计,如图2(a)所示,仿生晶胞单元两端为椭圆弧,并由其切线相连接,构成类似虾螯的锥形结构. 仿生晶胞单元安置于外管和内管间,中部位置由中间管贯穿连接,构成类似虾螯结构中的两个腔体. 设计的仿生薄壁管结构命名为T1,其外管、中间管和内管对应尺寸分别为D1=70 mm、D2=44 mm、D3=18 mm,并通过仿生晶胞单元连接. 为开展对比试验,将仿生晶胞单元改由薄壁肋板替代,设计了普通薄壁管T2,如图2(b)所示.
本研究将管厚度t和仿生晶胞数目n作为试验因素,探讨各因素对薄壁管吸能特性影响规律,各因素共分为5个等间距水平,如表1所示,不同晶胞数目薄壁管分别命名为T1_2(2晶胞)、T1_3(3晶胞)等. 其中,考虑到碰撞过程中薄壁管的稳定性,薄壁管高度设置为160 mm.

因素水平12345晶胞数n23456厚度t/mm0.51.01.52.02.5
在仿真计算时,选用6A02铝合金作为仿生薄壁管的材料,Hypermesh中对应材料为MATL24,有限元模型的参数如表2所示,网格划分为边长尺寸为2 mm的正方形. 薄壁管顶端施加1 000 kg的刚性墙,碰撞速度设置为10 m/s,如图3所示.

表2 有限元模型参数设置Tab.2 Parameteres of finite element model
轴向碰撞时,对薄壁管底端节点施加6个自由度的约束,径向碰撞时,对其底部侧面进行6个自由度的约束. 模型参数设置完成后,导出K文件并通过Ls-Dyna软件对轴向动态载荷作用下的薄壁管进行仿真分析. 径向碰撞条件下,需要考虑刚性墙与薄壁管不同初始接触位置对吸能特性可能产生的影响,文中主要考虑2种工况(图3(b)),刚性墙与薄壁管初始接触点位于某一晶胞单元正上方(T1_2)以及位于相邻晶胞单元正中间(T1_2_R),后者在前者基础上绕轴线旋转一定角度(180度除以晶胞数).
1.3 吸能特性指标
1.3.1峰值载荷(peak crush force,PCF)
峰值载荷表示碰撞发生时薄壁管在变形过程中出现的冲击载荷峰值. 过大峰值载荷的会导致碰撞的加速度较大,对车内乘员造成损伤.
1.3.2平均载荷(mean crush force,MCF)
平均载荷表示碰撞过程中薄壁管发生塑性变形吸收的能量与薄壁管变形位移的比值,即
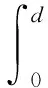
(1)
式中:EP为薄壁管吸收的能量;F(x)为变形过程中的瞬时载荷;d为薄壁管变形位移.
1.3.3比吸能(specific energy absorption,SEA)
比吸能为单位质量的能量吸收率,它表示碰撞过程中薄壁管发生塑性变形吸收的能量与薄壁管质量的比值,即
RSEA=EP/m,
(2)
式中:m为薄壁管质量. 由于薄壁管轻量化设计的要求,薄壁管在碰撞过程中,比吸能是薄壁管吸能特性的重要指标[3].
1.3.4碰撞力效率(crush force efficiency,CFE)
碰撞力效率为平均载荷与峰值载荷的比值,碰撞力效率越大,平均载荷越接近峰值载荷,表明碰撞过程中薄壁管载荷波动较小,其吸能特性较为优异,其表达式为
ηCFE=FMCF/FPCF.
(3)
2 结果分析
2.1 轴向吸能特性
轴向碰撞条件下,峰值载荷、比吸能和碰撞力效率随壁厚以及晶胞单元数变化规律如图4所示. 由图4(a)和4(b)可知,峰值载荷和平均载荷随壁厚呈现线性增加,平均增加率分别达到54.2%和83.7%. 相同壁厚条件下,峰值载荷随晶胞数增加,变化较为平缓,平均增加了10.1%,平均载荷增加了15.1%,由此可见,壁厚对峰值载荷和平均载荷的影响明显较晶胞数的大.
由图4(c)可知,随着壁厚增加,比吸能平均增加了18.9%. 比吸能随晶胞数增加,平均变化率为4.9%. 由图4(d)可知,碰撞力效率范围为35.1%~77.7%. 碰撞力效率随壁厚增加,平均增加率为17.1%,其中,壁厚由1.5 mm增加到2.5 mm时,碰撞力效率平均仅增加了9.4%. 碰撞力效率随晶胞数增加,变化较小,平均增加率仅为4.6%,这与比吸能随晶胞数变化规律相似.
轴向碰撞条件下,仿生薄壁管峰值载荷、平均载荷、比吸能和碰撞力效率均较普通薄壁管的分别提高了23.5%、37.4%、11.1%和11.2%.
结果表明,壁厚和晶胞数对峰值载荷和平均载荷的影响明显较比吸能和碰撞力效率的大,且壁厚对轴向吸能特性的影响较晶胞数的大.
2.2 径向吸能特性
径向碰撞条件下,仿生薄壁管吸能特性如图5所示. 由图5(a)和5(b)可知,峰值载荷和平均载荷随壁厚增加而增加,平均增加率分别为131.3%和126.2%. 当壁厚达到1.5 mm时,峰值载荷急剧增加,最大峰值载荷到达431.2 kN,分析是由于薄壁管自身相互挤压密实,产生了较大的峰值载荷. 峰值载荷和平均载荷随晶胞数的变化趋势相同,平均增加率约为30%.
由图5可知,比吸能随壁厚增加而增加,平均增加率达到45.4%,厚度由2.0 mm增加到2.5 mm时,比吸能增加较小,平均增加率为18.0%. 比吸能随着晶胞数增加而增加,且增加趋势逐渐平缓,平均增加率为18.6%. 由图5(d)可知,对于不同晶胞数薄壁管,碰撞力效率随壁厚变化呈现不同波动趋势,对于2、3和5晶胞管,碰撞力效率随壁厚增加呈现先减少后增加趋势;对于4和6晶胞管,碰撞力效率随壁厚增加,先增加后减少. 除3晶胞管外,碰撞力效率随晶胞数增加,总体上呈现增加趋势,平均增加率为11.7%,值得注意的是,当晶胞数达到5以后,碰撞力效率均超过了50%.
径向碰撞条件下,仿生薄壁管峰值载荷和比吸能均较普通薄壁管的大,分别平均增加了41.2%和24.6%,仿生薄壁管碰撞力效率较普通薄壁管提高了37.8%. 仿生薄壁管平均载荷始终较普通薄壁管的大,平均增加率为80.2%. 由此可见,仿生薄壁管径向吸能特性优于普通薄壁管.
进一步对刚性墙与薄壁管不同初始接触位置(图3(b))时的径向吸能特性进行分析,采用平均变化率进行描述,其表达式为
η=(ki-kj)/kj×100%,
(4)
式中:kj为刚性墙与薄壁管初始碰撞接触点位于某一晶胞单元正上方时的吸能特性指标值:ki为初始碰撞接触点位于相邻晶胞单元正中间时的吸能特性指标值;η为二者之间的平均变化率,数值如表3所示. 不同工况下仿生薄壁管径向变形模式如图6所示.
表3 不同初始接触位置吸能特性指标平均变化率η
Tab.3 Average change rate of lateral energy absorption under different contact position

晶胞数n峰值载荷/%平均载荷/%比吸能/%碰撞力效率/%2-4.8-8.4-7.1-11.13 24.526.21.1-0.74-33.4-36.6-28.39.657.5-4.00.912.967.46.110.72.1
由表3可知,n=2时,T1_2_R各项吸能特性指标值较T1_2的小,这是由于T1_2_R状态的晶胞处于水平位置,不能对竖直方向的碰撞载荷进行较好的吸能(图6);n=3时,T1_3_R峰值载荷和平均载荷较T1_3的增加了25%左右,但其比吸能和碰撞力效率变化不超过2%;n=4时,的T1_4_R变化最为明显,除碰撞力效率有所提管高外,其他吸能特性指标值均减少,其中,比吸能减少了28.3%,表明其吸能效果明显变差;n=5时,T1_5_R的碰撞效率增加了12.9%,比吸能变化较小;n=6时,T1_6_R各项吸能特性指标值较T1_6的大,其中,比吸能增加了10.7%.
由图6发现,偶数晶胞时,薄壁管呈现近似菱形或矩形变形模式,对于4和6晶胞,矩形变形模式更利于提高吸能,而奇数晶胞则呈现梯形(T1_3_R和T1_5)或倒梯形(T1_3和T1_5_R)变形模式,且倒梯形变形的吸能特性优于梯形变形的. 另外,当薄壁管晶胞数达到5以后,初始碰撞接触点位于晶胞单元正上方时的吸能效果,较初始碰撞接触点位于相邻晶胞单元正中间时的好.
综上所述,径向碰撞条件下,薄壁管峰值载荷和平均载荷随壁厚变化最明显,其次是比吸能,碰撞力效率的变化最小,另外,壁厚对径向吸能特性的影响较晶胞数的大.
3 结构尺寸优化
通过上述分析可知,轴向和径向碰撞条件下,仿生薄壁管峰值载荷和平均载荷较大,需要对仿生管的结构进行优化. 优化的目标是以峰值载荷值低于200 kN为约束条件[9],获取最小的薄壁管平均载荷,以及最大的比吸能和碰撞率效率.
文中采用响应面法对薄壁管结构进行优化,寻求最优结构尺寸. 以薄壁管厚度和仿生晶胞单元数目为变量,平均载荷、比吸能和碰撞力效率为优化指标,获取各指标响应面,优化的数学模型如下:
min:FPCF=f1(t,n),min:FMCF=f2(t,n),
max:RSEA=f3(t,n),max:ηCFE=f4(t,n),
(5)
式中:f1(t,n)、f2(t,n)、f3(t,n)和f4(t,n)分别为峰值载荷、平均载荷、比吸能和碰撞力效率关于厚度和仿生晶胞单元数目的目标函数,其表达式为
(6)
式中,i和j为变量的幂次,最大值取4,即目标函数是关于厚度和仿生晶胞单元数目的4次函数. 作为耐撞性能的重要参考指标,薄壁管的比吸能和碰撞力效率越大表明吸能效果越好,峰值载荷和平均载荷越小,表明碰撞时造成的伤害越小;通过选取合适的变量和目标函数以及合理的边界条件,利用响应面法得到满足边界条件的有效解,从中选取最优解.
通过上述仿真结果,得到轴向和径向碰撞条件下仿生薄壁管平均载荷、比吸能以及碰撞力效率的响应面. 仿真值与响应面值相对误差在8.4%以内,表明模型(6)能较准确描述薄壁管吸能特性. 以峰值载荷小于200 kN为约束条件,在不同晶胞数和壁厚条件下,寻找满足约束的较优解,如表4所示.

表4 响应面得到的较优解Tab.4 Superior solutions from response surface
通过进一步对比,轴向碰撞时,比吸能最大值出现在晶胞数为4和5条件下,但n=4时的平均载荷更小,且碰撞力效率较后者的大. 因此,轴向碰撞条件下最优解为:n=4、t=1.28 mm,对应平均载荷、比吸能和碰撞力效率分别为117.2 kN、26.9 kJ/kg和58.3%. 径向碰撞条件下,n=5时的比吸能最大,其次为n=6,前者平均载荷比后者的增加了7.4%,但比吸能提高了8.3%. 因此,轴向碰撞条件下最优解为:n=5、t=1.81 mm,对应的平均载荷、比吸能和碰撞力效率分别为119.3 kN、11.4 kJ/kg和56.2%.
对最优结构尺寸薄壁管进行有限元仿真验证,得到轴向碰撞条件下,n=4、t=1.28 mm时,FPCF=198.7 kN,FMCF=117.1 kN,RSEA=27.0 kJ/kg和ηCFE=59.0%;径向碰撞条件下,n=5、t=1.81 mm时,FPCF=195.2 kN,FMCF=112.0 kN,RSEA=10.8 kJ/kg和ηCFE=57.4%,与响应面计算结果的误差范围为-2.0% ~ 5.1%,表明响应面模型能较好的描述仿生薄壁管吸能特性.
综合考虑轴向和径向碰撞条件下薄壁管吸能特性,通过对平均载荷、比吸能和碰撞力效率进行加权[10-12](如式(7)所示),获取薄壁管最优结构尺寸.

式中:W为薄壁管吸能特性指标加权值,量纲一的,W值越大,表明薄壁管轴向和径向综合吸能特性最优;λ1,λ2和λ3为吸能特性指标加权系数,λ1+λ2+λ3=1,文中λ1,λ2和λ3值分别取为0.3、0.4和0.3.FMCFmax、RSEAmax和ηCFEmax分别为平均载荷、比吸能和碰撞力效率最大值,用于各吸能特性指标的量纲一化处理.
以峰值载荷小于200 kN为约束条件,通过响应面计算不同晶胞数和壁厚条件下平均载荷、比吸能和碰撞力效率,通过式(7)得到不同晶胞数下薄壁管吸能特性指标加权值. 不同晶胞数下的最优加权值,如表5所示.

表5 薄壁管吸能特性指标较优加权值Tab.5 Superior weighted value of energy absorption indicators of thin-walled tube
由表5可知,n=4、t=1.55 mm时,W有最大值0.827.
进一步通过仿真和试验进行对比验证,载荷随位移变化规律如图7所示. 由图7可以看出,仿真和试验的载荷波形的变化曲线基本一致,说明仿真分析是有效可行的. 轴向和径向碰撞条件下,平均载荷、比吸能和碰撞力效率仿真值和试验值如表6所示. 由表6可知,试验值和仿真值的平均相对误差不超过7%,表明仿真模型和方法能较好地反映实际试验.

表6 吸能指标仿真与试验值对比Tab.6 Comparison of energy absorption indicators between simulation and testing value
4 结 论
结合雀尾螳螂虾螯耐撞性结构特征,利用结构仿生原理设计了一种具有仿生晶胞单元的高效吸能薄壁管,并对薄壁管轴向和径向碰撞吸能特性进行有限元仿真. 仿真结果表明轴向和径向碰撞条件下,壁厚和晶胞数对峰值载荷和平均载荷的影响较比吸能和碰撞力效率的大,且壁厚对吸能特性的影响较晶胞数的明显;仿生薄壁管比吸能随壁厚增加,平均增加率分别为18.9%(轴向)和45.4%(径向). 轴向碰撞条件下,仿生薄壁管峰值载荷、平均载荷、比吸能和碰撞力效率均较普通薄壁管的分别提高了23.5%、37.4%、11.1%和11.2%. 径向碰撞条件下,仿生薄壁管峰值载荷和比吸能均较普通薄壁管的大,分别平均增加了41.2%和24.6%,仿生薄壁管碰撞力效率较普通薄壁管提高了37.8%. 仿生薄壁管尺寸优化结果表明,4晶胞仿生薄壁管,壁厚0.9 mm时具有最优解,比吸能分别为24.00 kJ·kg-1(轴向)和3.97 kJ·kg-1和(径向),试验值和仿真值的平均相对误差不超过7%,表明仿真模型和方法具有可靠性,可为薄壁管结构轻量化设计提供参考.
