基于闭包准则和成对约束的半监督聚类算法

向力宏，金应华，徐圣兵

（广东工业大学应用数学学院，广东广州510520）

聚类分析是数据挖掘的重要组成部分，其作为常用的数据分析方法被广泛应用于人工智能、模式识别和机器学习领域中。以往的机器学习一般只考虑无标签和有标签两类课题，使用的方法有无监督学习和监督学习。传统的聚类分析主要是无监督学习，如K-means聚类［1］、分层聚类［2］、密度聚类［3］、极大熵聚类［4］等，对于有标签的数据往往采用监督学习方法，如 k-近邻［5］、决策树［6］、支持向量机［7］等。

现实生活中我们所获得的数据大多是复杂的，数据中不仅包含了未标记数据，而且还包含了标记数据，无监督学习和监督学习在对这类数据进行模式求解的过程中所得到的模型精度一般。因此如何解决样本数据标签不充分所导致的聚类数据性能下降问题，是近年来机器学习领域研究的方向之一。半监督学习算法能够较好地解决以上问题，该方法能够利用少量已有样本数据标记监督信息进行分类。

现有的半监督聚类形式一般通过两种先验信息来指导算法聚类，即标记信息和成对约束信息，由于标记信息能够转化为成对约束信息，我们将所得到的成对约束信息设置为半监督聚类先验信息来进行监督聚类。聚类算法通过标记信息的引导来推进聚类过程的划分调整，从而不断改善聚类效果，这类半监督聚类算法已经有了大量开创性研究，例如，尹学松等［8］提出了基于成对约束的判别型半监督聚类分析方法解决了高维数据计算性能不足和成对约束的违反问题；肖宇等［9］基于近邻传播算法，运用标签类数据和成对约束数据构成的相似度矩阵进行聚类指导，进而提高近邻传播方法的聚类性能；王君言等［10］基于DL1图和KNN图叠加图的高光谱图像半监督分类算法，构建了空谱信息联合的图框架结构，提高小样本高光谱图像自动分类的精度。成对约束信息是一种普遍存在于样本数据之间的相互信息，这对于研究聚类过程具有十分重大的意义。

本文延着向思源等［11］（PD-sSC算法）的研究思路，提出了一种基于闭包准则的成对约束打包算法（CCPC），该算法解决了聚类过程不受成对约束数目变大而导致的聚类性能相对下降的问题。在不降低聚类效果的前提下，提出了一种程序改进方法，降低了编程难度。实验结果表明了CCPC算法的有效性。

1 算法

1.1 构建成对约束及闭包

首先对本文所需要的数学符号进行定义，如表1所示。

表1 CCPC目标函数符号定义

假设给定样本集合空间 X=｛xi│xi∈Rd，i=1，2，…，n｝，其中，n 表示样本点数，R 为实数，d 为样本维数。本文所采用的成对约束可分为must-link约束和cannot-link约束，并将所有must-link集合记为ML，所有cannot-link集合记为CL，两者的定义如下：

定义1 must-link，定义集合ML=｛（xi，xj）│i＜j｝，若两个样本满足（xi，xj）∈ML，则表明xi和xj两个样本属于同一类，也称xi和xj存在正关联约束关系。

图1为成对约束must-link约束示意图，样本点用球表示，虚线围成的区域样本为同一类簇，实心圆分别代表样本点xi和xj，两个样本点之间通过直线连接表示must-link约束，说明xi和xj属于同一类簇，满足正关联约束条件。

图1 must-link约束关系示意图

定义2 cannot-link，定义集合CL=｛（xk，xl）│k＜l｝，若（xk，xl）∈CL，则表明xk和xl两个样本不属于同一类，也称xk和xl存在负关联约束关系。

图2为成对约束cannot-link示意图，球形所表示的含义与图1一致，实心圆分别代表样本点xk和xl，两个样本点之间通过虚线连接表示cannot-link约束，说明两个样本点在聚类过程中分别属于不同的类簇，满足负关联约束条件。

图2 cannot-link约束关系示意图

受尹学松等［8］研究的启发，本文先基于must-link约束类对数据进行打包处理，降低原始数据成对约束容量，重新构造新的cannot-link约束，使得算法在聚类过程中不会产生违反must-link约束问题，为了便于理解对闭包准则进行如下定义。

定义 3 假设有 3 个样本 a1，a2，a3，满足（a1，a2）∈ML，（a1，a3）∈ML，则（a2，a3）∈ML，此时称 a1，a2，a3构成的集合为同类闭包，简称闭包。类似地，可定义含有任意有限个样本点的同类闭包。若在某样本点处没有must-link约束，此时可约定该样本点就是一个独立的同类闭包。

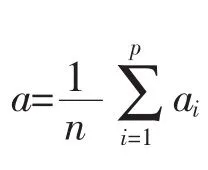
定义5设两个闭包为A=｛a1，a2，…，aq｝和B=｛b1，b2，…，bp｝。若存在（ai，bj）∈CL，其中ai∈A，bj∈B，则称A，B为异类闭包。

一旦完成基于must-link约束类的打包，就可以用闭包中心替代整个闭包；若两个闭包中的样本点之间存在cannot-link约束，此时可设定对应的两个闭包中心之间存在cannot-link约束。如图3所示，已知两个闭包｛a1，a2，a3，a4｝和｛b1，b2，b3｝，a，b 分别为闭包中心，其中实线表示 must-link约束，虚线表示cannot-link约束，黑色节点为样本点，白色节点为闭包中心；此闭包之间存在一对cannot-link约束，即（a1，b1）；打包完成后，可设定 cannot-link约束（a，b）来表示原始样本的 cannot-link约束（a1，b1）。

图3 must-link约束合成及cannot-link约束的闭包转换示意图

在完成打包操作并更新cannot-link约束后，会得到一组新样本，记为，其中 nml为样本量。一般地，nml＜n；另记，更新后的cannot-link约束集合为CL'。

尹学松等［8］基于数据打包操作设计了PCBKM聚类算法。经过分析和实验，可知该算法有如下两方面不足。1）在与PD-sSC算法［1］进行实验对比时发现，PCBKM算法在成对约束数目相对较大时表现优异，但在成对约束数目较小时，聚类效果比不上PD-sSC算法。2）PCBKM算法中step-2-（b）步骤对cannot-link约束处理得太过简单，没有考虑异类闭包之间可能存在的复杂的分布形式。若采用step-2-（b）步骤进行计算，不同异类闭包对的选择会产生不同的聚类结果。图4列举了较复杂的异类闭包对的分布形式，其中带编号的白色圆形节点为闭包中心（新样本点），虚线表示cannot-link约束，椭圆结构表示计算过程中可以选择的异类闭包对。以图4的第1幅图为例，存在3对异类闭包配对（1，2），（1，3），（2，3）；当用PCBKM算法中step-2-（b）步骤分别处理这三对异类闭包的cannot-link约束时，三个闭包点｛1，2，3｝都有两个聚类结果，此时可能出现同一闭包点在不同异类闭包的cannot-link约束对下得到不同的聚类结果。如果想改进step-2-（b）步骤中的这点不足，需要充分考虑异类闭包对的分布形式，但是异类闭包对的分布形式不可枚举，图4仅列举了几类简单的情况。

图4 异类闭包选取结构示意图

为了解决以上两个问题，本文提出一种基于闭包准则的成对约束打包算法（CCPC）。

1.2 MEC中熵项的推广

一般称经典MEC聚类算法［12，14-18］所含的熵项为自信息熵，其仅能刻画样本点的内部信息，代表样本点自身的信息。在聚类过程中不仅需要利用样本内部的信息，还需要挖掘利用其外部之间的信息。向思源等［11］引入了功效散度（power-divergence,PD）族，它可度量两个概率向量之间的距离，概率向量之间相似度越高，对应的PD散度越小。具体定义如下：

由定义6可知，PD散度是一族，当指标p=0时PD散度也为KL（Kullback-Leibler）散度［19］，即样本对之间的相对熵。以下给出KL散度的明确定义。

李晁铭等［13］利用相对熵（KL散度）构造了CE-sSC聚类算法。PD散度可随着指标p的改变而改变，还可将PD散度推广到更一般的形式，例如ø散度［20］。基于PD散度和相对熵之间的关系，向思源等［11］在李晁铭等［13］研究成果的基础上提出了基于PD散度的PD-sSC聚类算法，克服了CE-sSC算法中熵项之间的干扰问题，提高了惩罚系数的选择效率。

1.3 目标函数

定义 8 惩罚系数矩阵 Γ=（Γjk）nml×nml

显然，Γ为上三角形矩阵，其中所有γjk元素皆为正数。类似于PD-sSC算法，通过融合惩罚项系数和PD散度得到目标函数的惩罚项为

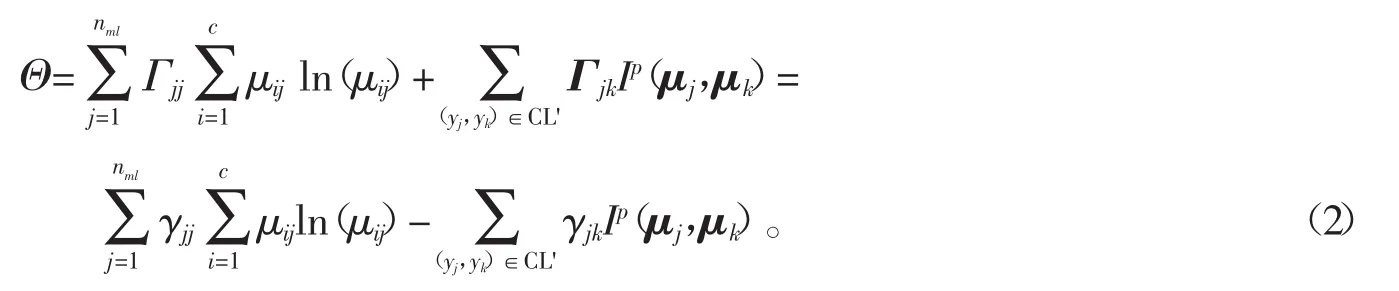
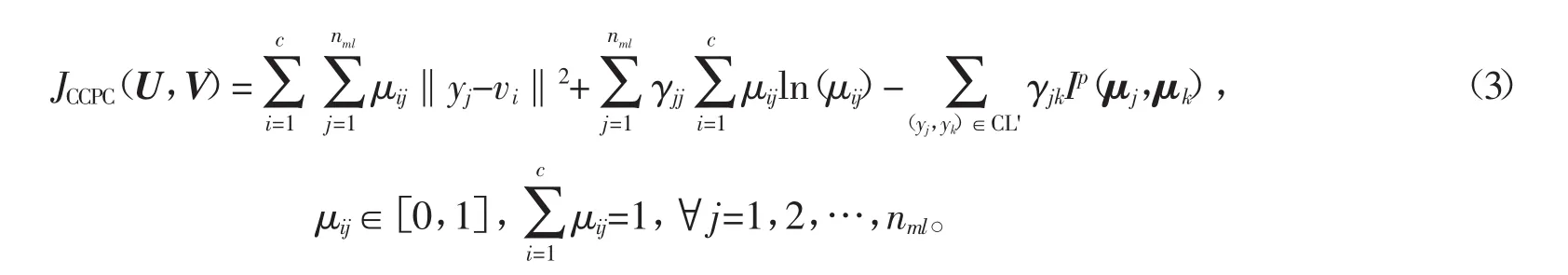
1.4 参数求解

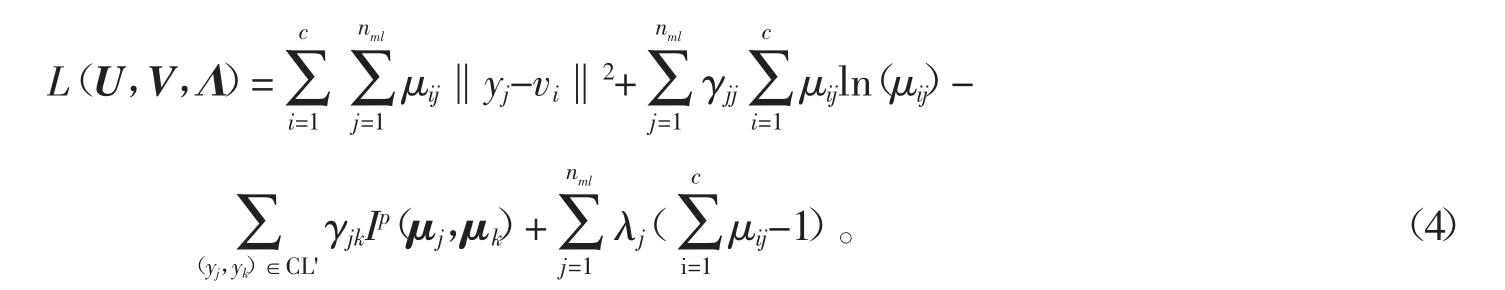
由式（5）可得

将式（8）变形得到

将式（9）代入到式（6）可以得到隶属度迭代公式为

式（6）～（10）中的参数 aij定义如下

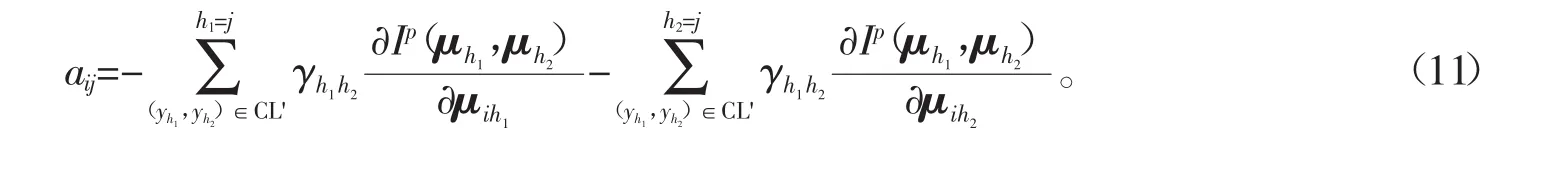
2 算法流程

总结上述推导，得到CCPC算法的具体流程如下：

输入原始目标数据集Y，惩罚系数矩阵Γ＝（Γjk）nml×nml，初始隶属度矩阵U(0)，聚类数c（2≤c≤nml），PD散度指标p，算法最大迭代次数T，终止条件ε。

输出 最优隶属度矩阵U和聚类中心V。

迭代过程为：

（1）初始化迭代计数器t=0；

（2）根据式（7）和 U(t)计算出 V(t)；

（3）根据式（10）和 V(t)更新 U(t)为 U(t+1)；

（4）当‖U(t+1)-U(t)‖≤ε或t=T时，终止算法运算；否则，令t=t+1返回到（2）；

（5）算法收敛后，输出最优隶属度矩阵U和聚类中心V。

以上算法是对打包后的样本集合Y进行聚类分析，在打包规则的基础上，可将此聚类分析结果反射到原样本集合X上，至此才算完成原样本组的聚类分析。图5列出了CCPC算法的基本框架。

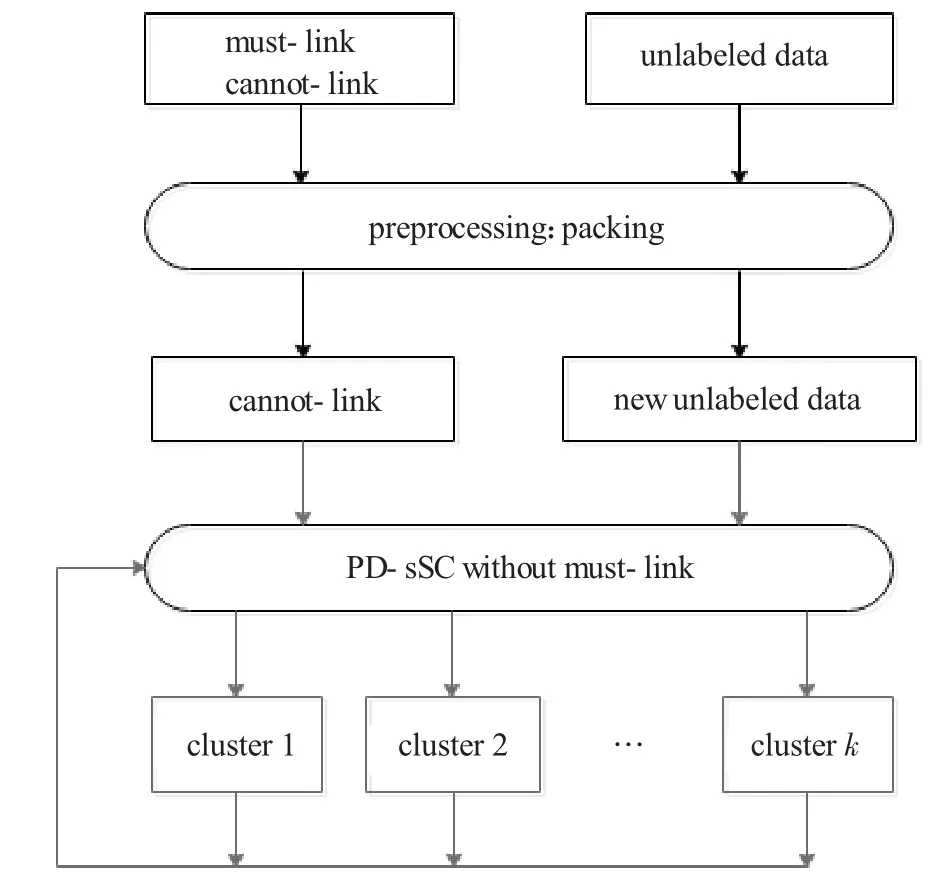
图5 CCPC算法的框架图

在编程实现CCPC算法的过程中，对隶属度向量(10)式进行归一化操作时，很容易碰到算术溢出问题，此时就需要对算法流程加入若干相应的控制项，这给编程带来了难度。为解决这一问题，定义如下的截尾指数函数

3 实验及分析

本文选取6个数据集对CCPC算法和其他相关的聚类算法进行实验比较。

3.1 实验数据与评价准则

实验选取了UCI数据库中的四组常用数据集，分别为breast、iris、seeds、wine数据，还选取了池塘水质评价水色图像特征数据集X1和用于区域环境质量状况评价的空气质量数据集X2作为实验数据。选取以上数据集的原因是算法性能检测的结果直观可靠，表2列出了数据集的特征描述。

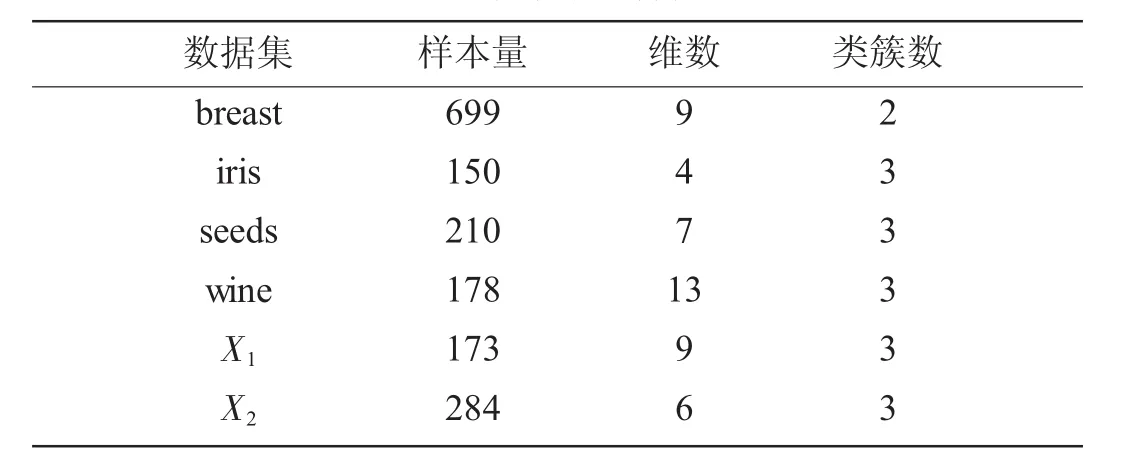
表2 数据集的特征

在进行实验之前，对所有数据集进行中心化与标准化处理，目的是消除量纲差异。本文选择的对比算法有基于功效散度和成对约束的半监督聚类的PD-sS算法［11］、基于成对约束的交叉熵半监督聚类的CE-sSC算法［13］、基于成对约束的K均值聚类的PCBKM算法［8］和基于谱图和成对约束的主动半监督聚类 SSC 算法［20］。

实验对比中采用了三种评价指标：1）准确率指标（Accuracy Cluster，AC）：评价聚类准确程度；2）标准互信息指标（Normalized Mutual Information，NMI）：衡量两个数据分布的吻合程度；3）兰德指数（Rand Index，RI）：评价算法聚类结果与真实情况的吻合程度。以上三种评价指标的取值都在0至1之间，指标值越接近1就说明聚类效果越好，使用多个评价指标进行对比能够更加充分地评价聚类效果。

3.2 实验设计与结果分析

实验前，先采取数据清洗操作，然后通过随机抽样方式构建成对约束信息，在实验过程中，忽略数据的标签信息。根据数据样本量和实验结果选取成对约束的数量点，具体信息如下：breast数据的成对约束数目设置为 20、40、60、80、100、120、140、160、180、200；iris 数据成对约束数目设置为 10、15、20、25、30、35、40、45、50、55；seeds、X2数据的成对约束数目设置为 10、20、30、40、50、60、70、80、90、100；wine、X1数据的成对约束数目设置为 8、16、24、32、40、48、56、64、72、80。进行 1 000 次重复实验，求得评价指标的平均值，将该平均值当作评价指标的估计值。在实验中，CCPC算法的实验参数为：功效指标p=-1，算法迭代终止条件ε=1e-5，最大迭代次数T=100。图6～11依次列出了表2中数据集的评价指标估计，其中横坐标为成对约束数目，每幅图中的纵坐标分别为AC、NMI、RI评价指标估计值。

图6 breast数据集实验结果

图7 iris数据集实验结果

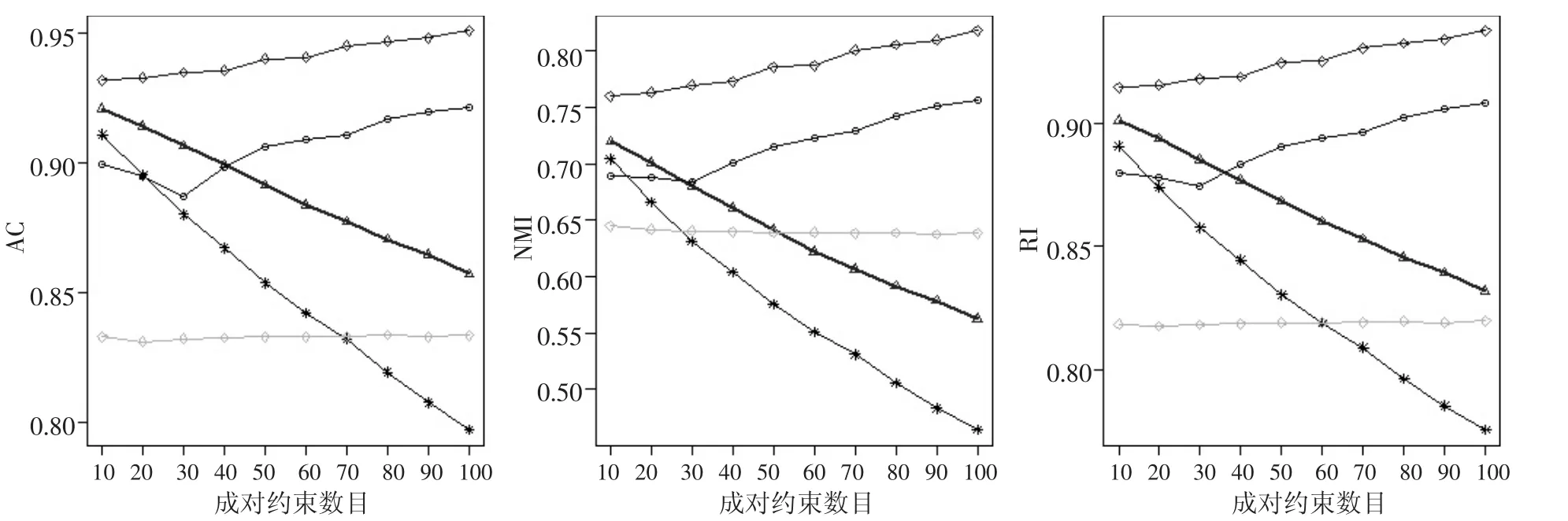
图8 seeds数据集实验结果

图9 wine数据集实验结果

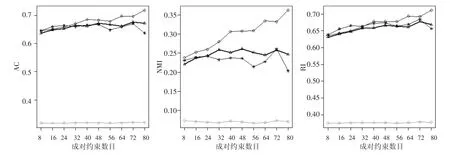
图10 X1数据集实验结果

图11 X2数据集实验结果

从图6可看出，CCPC算法对应的三个评价指标都是最高的，聚类效果表现最好。由于breast数据量相对较大，对比算法的SSC算法运算速度不佳，因此在计算过程中不考虑SSC算法的主动学习部分，只研究其半监督聚类算法。在成对约束数目不断增加的过程中，PD-sSC、CE-sSC和PCBKM算法的三个指标值都显示下降趋势，其中PCBKM算法的降幅最大，此趋势是因为选择了固定的惩罚项系数，此时，当成对约束数目增加时，目标函数中的惩罚项相对比重会增加，从而影响了聚类效果。但CCPC算法评价指标却基本呈现上升趋势，图6～11都有该现象，这是CCPC算法的优点，即对惩罚系数的选择不敏感，具有抗干扰性。

从图7可看出，CCPC算法的AC与RI指标值都比其他4个算法高，NMI指标值也仅次于SSC算法。随着成对约束数目的增加，CCPC算法与PCBKM算法的评价指标是单增的，PD-sSC和CE-sSC算法存在明显的下降趋势。虽然SSC算法的NMI指标值最优，但是SSC算法包含两个对算法影响较大的超参数，并且算法运算时间较长，因此SSC算法不是最好的选择。

从图8可看出，CCPC算法的三个评价指标也是优于其他4个算法，且值都高于0.8。当成对约束数目大于30时，PD-sSC和CE-sSC算法随着成对约束数目的增加，聚类性能不断下降，而CCPC算法保持了与PCBKM算法相近的增加值，该现象说明了闭包准则能有效提高聚类效果，CCPC算法吸取了PCBKM算法的优点。从图9也可看出，CCPC算法的3个指标值都要优于其他4个算法，算法性能与seeds数据相似，3个指标值都大于0.8，进一步表明CCPC算法聚类效果最好。

从图10可看出，当成对约束小于32的时候，除了SSC算法其他4个算法的AC、NMI和RI指标值之间差别较小，随着成对约束数目的增加，CCPC算法的增长趋势明显优于其他算法，说明聚类效果优于其他4个算法。从图11可看出，PCBKM算法在X2数据中聚类表现最好，当成对约束数目不足时，PD-sSC和PCBKM算法性能会出现小幅度下降，而当成对约束数目在20至70区间范围内取值时，CE-sSC算法优于CCPC和PD-sSC算法且三类算法效果都保持递增趋势。在接下来不断增加的过程中，CCPC算法的评价值也不断上升。

综合图6～11的结果，可得出CCPC算法有较好的聚类效果。在成对约束数目增加的情况下，CCPC算法的聚类性能呈现出上升趋势；一旦成对约束数目较为充分时，CCPC算法就能够给出优于其他算法的聚类结果。总体上，可以得出如下结论：CCPC算法优于对比算法。

4 结语

为解决PD-sSC算法在处理成对约束数目相对较多时聚类性能不够理想的问题，本文提出了基于闭包准则和成对约束的半监督聚类算法（CCPC）。该算法通过引入PCBKM算法中基于must-link约束对样本进行打包的思想，得到了只带更新了的cannot-link约束的新样本组，再用PD-sSC算法进行聚类分析，最后根据打包原则将聚类结果反射到原样本组上；克服了PCBKM算法在处理cannot-link约束时的不足；糅合了PD-sSC算法和PCBKM算法的各自优点。实验结果表明，在成对约束数目较少时，CCPC算法在聚类性能上与PD-sSC算法保持一致；在成对约束数目相对较大时，CCPC算法在聚类性能上与PCBKM算法保持一致。因此，无论成对约束数目是大是小，CCPC算法都有不错的聚类效果。