阶梯形变截面压杆临界荷载的一种较精确算法

陈玉骥 ，郭浩宇 ,罗旗帜 ，2，马镇航

（1.佛山科学技术学院交通与土木建筑学院，广东佛山528000；2.湖南大学土木工程学院，湖南长沙410082）

压杆临界荷载的计算有解析法、数值法、能量法和半解析法等［1-9］。其中，瑞利-里兹法（Rayleigh-Ritz method）是计算压杆临界荷载的常见方法之一。用瑞利-里兹法计算时，需要假设挠曲线函数，挠曲线函数的假设与计算精度密切相关。一般而言，若挠曲线函数满足所有内力边界条件和位移边界条件，则计算精度较高。若挠曲线函数只取一项，虽然较简，但通常计算精度较差，除非所设挠曲线函数与实际情况十分接近（这样的假设比较困难）。取挠曲线函数两项甚至更多项，虽然计算精度可以提高，但因为能量积分较复杂且要涉及求解阶数大于1的稳定方程（特征方程），故相应计算量较大。对于阶梯形变截面压杆，按上述算法，不管是挠曲线函数取一项，还是取多项，由于都用一个挠曲线函数表示整个杆件的位移，故即使满足所有边界条件，以及在截面突变点，可以满足位移和转角连续条件，但因在截面突变点左右杆段抗弯刚度EI不同，故弯矩不连续，因而导致计算精度不高，除非挠曲线函数取较多的项，但相应会大幅增加计算量。

本文在挠曲线函数取一项的基础上，通过进行修正，使得在截面突变点，弯矩也可以满足连续条件。算例表明，以这样经过修正的挠曲线函数计算，可显著提高变截面压杆临界荷载的计算精度。

1 计算思路

对于阶梯形变截面压杆，杆件由若干等截面杆段组成。计算其临界荷载时，若挠曲线函数y（x）取

式中，A为任意参数，φ（x）为满足边界条件的位移试函数。则根据瑞利-里兹法可得压杆的临界荷载

式中，Ii为压杆在等截面杆段区间［xi，xi+1］的杆件截面惯性矩，m为等截面杆段总数。若挠曲线函数取n项

式中，Ai为任意参数，φi（x）为满足边界条件的位移试函数项，n为位移试函数总项数。则由能量变分原理

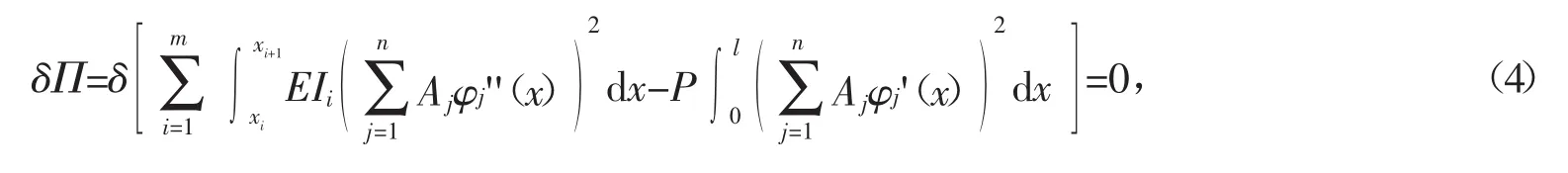
得齐次方程组

由相应的稳定方程，即可确定临界荷载。

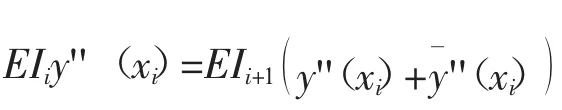
2 算例

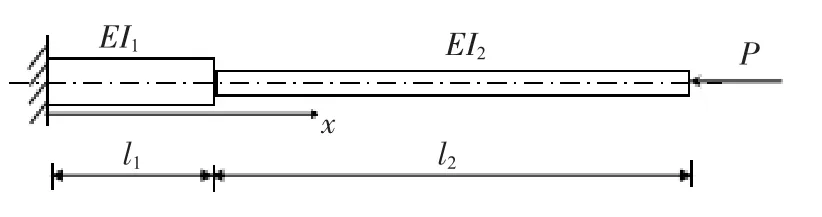
图1 变截面悬臂压杆

解1为了便于考察以下各种结果的精度，先确定该压杆临界荷载的精确解。文[10]中推导的两段阶梯形变截面悬臂压杆临界荷载的稳定方程为

对图1所示压杆，稳定方程为

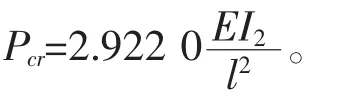
解2 挠曲线函数取一项（幂函数），设［10］

解3 挠曲线函数取两项,设［10］

解4 根据两个等截面杆段对应区间，分别假设挠曲线函数。其中，在区间［0，l/4］，仍然采用解2所设挠曲线函数；在区间［l/4，l］，则以在区间［0，l/4］杆段所设挠曲线函数中加入修正项来作为该杆段的挠曲线函数。该修正项的设置，必须保证在截面突变点满足连续条件。即在x=l/4时，修正项对应的挠度和转角为0，整个位移所对应的弯矩保持连续；此外在端点x=l处还需满足弯矩为0的条件。由于解2所设挠曲线函数可以满足图1所示压杆两端点的边界条件，故修正项可将其移轴l/4并将跨度改为区间［l/4，l］的跨度3l/4而得出。按照以上思路，假设挠曲线函数为

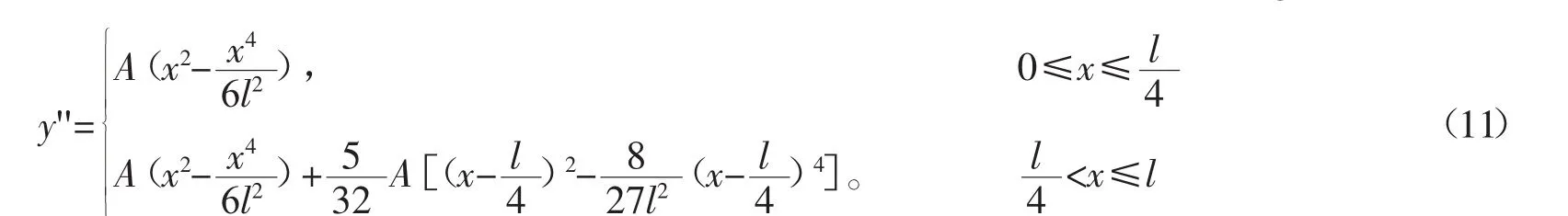
将该挠曲线函数代入（2）式，可求出

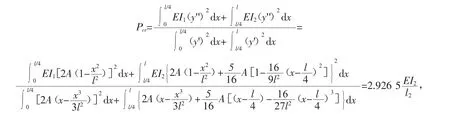
与精确解比较，误差0.154%。可见，该解的精度较未进行修正的解2和解3有了明显的提高。

解7 区间［l/4，l］采用解5所设挠曲线函数；对于区间［l/4，l］，在解5所设挠曲线函数中加入修正项，其思路与解4的相同。设

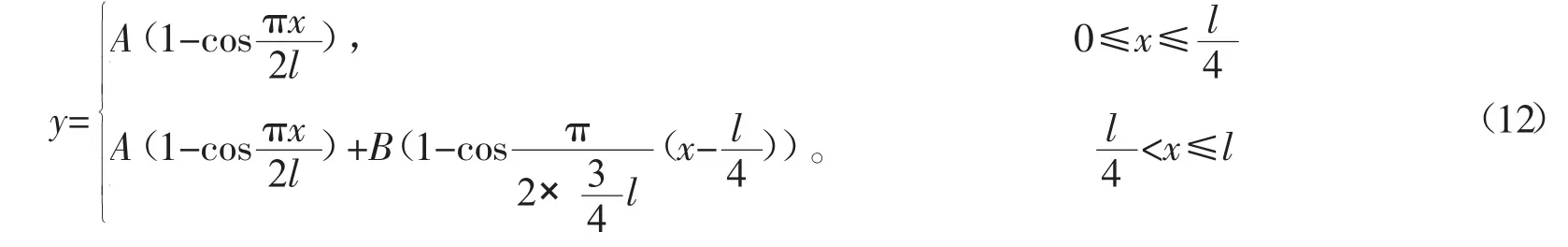
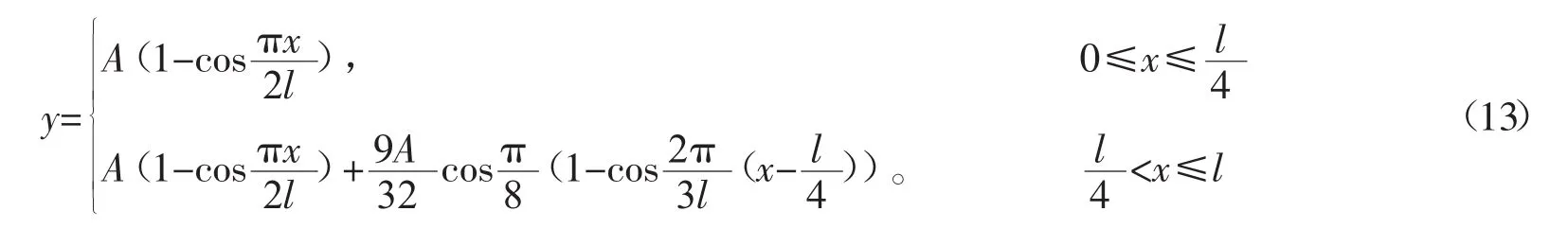
3 结语

通过以上计算表明，本文给出的修正项设置方法，可以大幅度提高计算精度，而计算量远较增加位移试函数项数要小，说明本文方法是阶梯形变截面压杆临界荷载的一种较精确算法。