震动载荷下含瓦斯煤动力学特征

孔祥国，王恩元，李树刚，胡少斌，鞠云强，李金铎

(1.西安科技大学 安全科学与工程学院，陕西 西安 710054; 2.教育部西部矿井开采及灾害防治重点实验室，陕西 西安 710054; 3.中国矿业大学 安全工程学院，江苏 徐州 221116; 4.河海大学 土木与交通学院，江苏 南京 210098)

随着煤矿开采深度的增加，地应力、瓦斯压力和瓦斯含量不断增高，采场结构也越来越复杂，应力和瓦斯复合动力灾害日趋严重且复杂[1-2]。煤炭开采过程中，远场震源，如顶底板断裂或活动、断层活化和震动放炮等人工扰动行为均会产生动载，引发冲击地压或煤与瓦斯突出，甚至使得发生灾害的临界指标参数降低[3-5]。当动载荷较小时，不会引起煤岩体宏观破坏，但有瓦斯的异常放散[2]，笔者将此类动载称之为震动载荷，研究震动载荷下含瓦斯煤体的动力学特性。

关于煤岩动力学特性的研究，主要借助霍普金森压杆试验系统，前人不断对霍普金森压杆系统进行改造以满足不同试验的要求，测试了多种煤岩动力学特性，为后续研究奠定了坚实的基础[6-8]。国外作者较早地开展了煤岩动力学特性测试，KLEPACKO J R等[9]研究了准静态载荷和冲击载荷下煤的动力学特性，OLSSON W A[10]发现了岩石强度应变率效应;宫凤强等[11]测试了一维动静组合加载下砂岩的动力学特性，发现相同应变率下岩石对外界冲击的响应受轴压比影响很大，动态冲击强度随轴压比的增加表现出先增加后减小的趋势;夏开文和姚伟[12]利用具有预加载装置的分离式霍普金森压杆系统研究了岩石在不同预拉伸应力下的拉伸强度，结果显示动态拉伸强度和总拉伸强度随着加载率的增加而增加，表现出明显的率相关性;朱晶晶等[13]使用大直径SHPB 试验装置，测试了循环冲击下花岗岩的动力学特性，变形模量和峰值应力均随着循环作用次数的增加而减小，但屈服应变相应增加;金解放等[14]分析了循环冲击下轴压和围压对砂岩能量耗散的影响，单位体积吸收能随平均应变率的增加而线性增加，当围压从低到高增加过程中，二者间拟合斜率随轴压的增加变化关系为“增加—基本不变—减小”;为了进一步阐释动静组合加载下岩石动力学机制;李夕兵等[15]结合统计损伤模型和黏弹性模型，建立了一维和三维动静组合加载本构模型，并通过试验结果进行拟合验证，从本质上解释了岩石动力学特性。

岩石动力学特性研究相对较早且成果丰富，煤体动力学主要基于岩石动力学而进一步发展。单仁亮等[16]研究了云驾岭矿无烟煤的动力学特性，发现初始弹性模量、屈服强度和极限强度均随着应变率的增加而提高;为了进一步完善煤体动力学，刘晓辉等[17]研究了不同应变率下煤样破坏模式，煤样在低应变率下多呈轴向劈裂破坏，高应变率下呈现出压碎破坏;冯俊军等[18]研究了动载荷下煤样的能量耗散机制，发现能量耗散与入射能和动态压缩强度呈正相关，说明试样破坏过程中高应力导致高能量释放;为了揭示煤体动力学作用机制，高文蛟等[19]提出了无烟煤单轴冲击强度理论，确定了动力学参数之间的定量关系，揭示了无烟煤多孔介质在冲击载荷下破坏机理;付玉凯等[20]运用弹塑性理论，建立了煤的损伤体-黏弹性本构模型，发现煤的动力学特性对高应变率较敏感;考虑到元件型模型解的不唯一性，王登科等[21]建立了煤的强度型统计损伤本构模型，能够有效地描述煤体动态破坏过程的力学特性。刘少虹等[22-23]分析了动静加载下煤的破坏特性，认为静载是改变原始裂隙的数量和裂隙尖端的蓄能，而动载使裂隙发生扩展进而破坏，煤岩体结构和动静载相互作用是诱发动力灾害的关键;相对于岩石赋存环境，煤层经常存在于富含瓦斯的环境之中，瓦斯对煤体动力学特性影响不可忽略，而这方面研究相对较少，因此含瓦斯煤动力学特性急需开展研究以进一步完善煤岩体动力学机制。

笔者主要开展震动载荷下含瓦斯煤动力学特性研究，考虑轴向静载、围压、瓦斯压力和动载荷冲击速度4个因素对含瓦斯煤动力学特征的影响，分析震动载荷下含瓦斯煤未宏观破裂时所表现的动力学特性，主要研究了含瓦斯煤峰值强度和峰值应变随各种因素的变化关系，并进一步分析了震动载荷下含瓦斯煤应变率效应，确立了峰值强度和峰值应变与应变率的关系，有助于揭示含瓦斯煤动力学机制。

1 试验系统、试样及测试原理

1.1 试验系统

在前人设计的霍普金森压杆基础上，自主建立了含瓦斯煤霍普金森压杆系统(SHPB-GAS)，实现了含瓦斯煤动力学特征测试的目标。含瓦斯煤霍普金森压杆系统主要由轴向静载加载子系统、围压加载子系统、瓦斯充放子系统、动载荷加载子系统、超动态应变采集子系统、红外测速子系统、气动发射装置、缓冲装置和抽真空系统等组成。含瓦斯煤霍普金森压杆系统示意简图如图1所示，该系统最主要组成是轴向静载子系统和动载荷加载子系统的主要杆件部分，分别是撞击杆(φ100 mm×40 cm)、入射杆(φ100 mm×5 m)和透射杆(φ100 mm×3 m),杆件均采用30Crmosini2a钢材制作，弹性模量210 GPa，纵波传播速度为5 100 m/s。

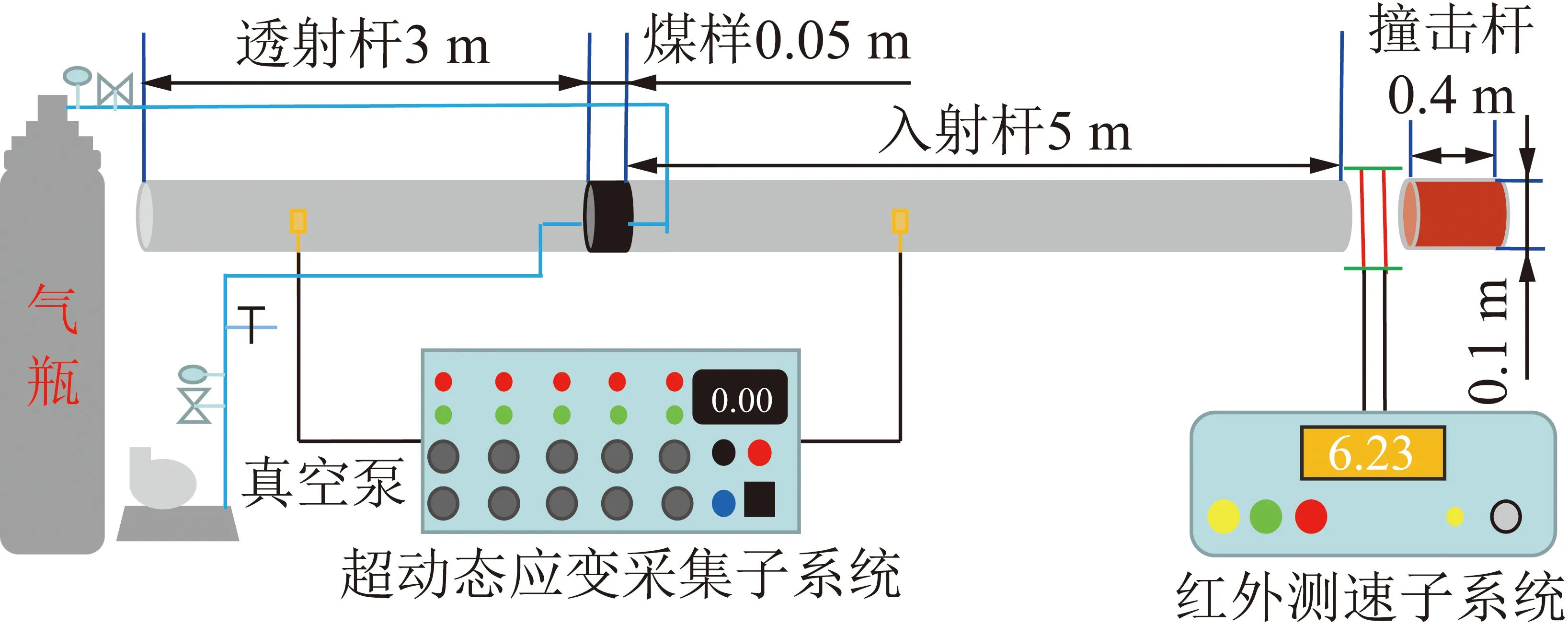
图1 含瓦斯煤霍普金森压杆实验系统Fig.1 SHPB-GAS experimental system

1.2 试样特征

此次试验所用煤样均选自杨庄煤矿，根据煤岩动力学测试要求，制成φ100 mm×50 mm的试样，经过打磨将试样两端平行度控制在0.02 mm公差范围内。为了减少试样的离散性，事先测试试样的波速并选择密度相近的试样进行试验，试验时在试样两端涂抹黄油以减少摩擦效应。所选试样的基本物理参数见表1。

表1 试样基本物理参数及试验结果
Table 1 Physical parameters of coal and experimental results

序号密度/(kg·m-3)轴向静载/MPa围压/MPa瓦斯压力/MPa冲击速度/(m·s-1)应变率/s-1峰值强度/MPa峰值应变11 4241.551.005.23154.1559.780.014 021 2473.051.005.23163.3775.700.014 531 3555.051.005.23170.2184.870.016 541 4777.051.005.23182.4387.220.019 951 2909.051.005.23245.6791.470.020 261 2855.021.005.23178.1152.780.020 071 2935.031.005.23177.0961.190.015 581 4875.061.005.23157.8777.830.014 591 3395.071.005.23153.3585.400.014 0101 3555.091.005.23143.2697.120.013 4111 4265.060.255.23166.3187.710.014 4121 2955.060.505.23160.7984.560.014 6131 4535.060.755.23156.0679.920.012 9141 3015.061.255.23136.3167.750.015 9151 3205.061.505.23139.6567.840.014 2161 3905.061.002.2978.8042.800.007 0171 3065.061.003.27121.6058.170.011 8181 4475.061.004.25135.3973.040.012 5191 3135.061.006.20180.7367.130.015 3

1.3 测试原理及过程

含瓦斯煤动力学测试原理与一维动载试验原理相同，仍是基于一维应力波假定和应力均匀化假设。试验过程中，将加工好的试样放入试验腔体，通过轴向静载子系统将轴向静载加载到预设压力;通过围压加载子系统向试样环向方向均匀的施加围压;关闭充气管路上的阀门，将放气管路与真空泵相连，进行4 h抽真空;关闭真空泵及放气管路上阀门，打开气瓶减压阀及充气管路阀门向试样内充入一定压力瓦斯，吸附4 h，待吸附平衡后关闭充气管路;启动空气压缩机使气动发射装置内压缩空气达到相应压力，设置红外测速子系统和超动态应变子系统到预触发界面;待准备工作全部做好，启动气动发射装置将撞击杆发射撞击入射杆，同时打开放气管路卸掉瓦斯，红外测速子系统会自动触发并测定撞击杆速度，超动态应变子系统通过贴于入射杆和透射杆上的应变片采集含瓦斯煤动力学实验过程中的应力波信号，如图2所示。

图2 采集到的应力波波形Fig.2 Collected stress wave

撞击杆撞击入射杆，形成应力波在入射杆中传播，当入射波到达入射杆与试样的接触界面，一部分被反射，另一部分进入试样传播，到达试样与透射杆接触界面又发生反射和透射，应力波在入射杆、试样和透射杆中传播会经过多次反射和透射。相比应力波脉冲长度，试样长度足够小，一般地认为应力波反射一个卸载波(反射波)到入射杆和经过试样透射一个加载波(透射波)到透射杆，试样应力即达到平衡。因此，在对应力波信号进行处理时，通过3波分离的方法只选取第1个入射波、反射波和透射波(图2)进行计算。

基于一维应力波假定和应力均匀化假设，可推导出试样的平均应变率、应变和应力：

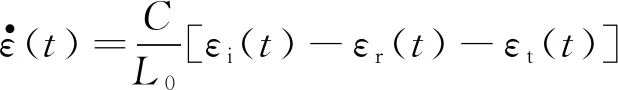
(1)

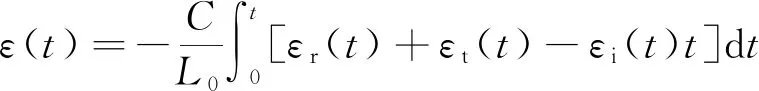
(2)

(3)

式中，C为应力波在弹性杆中传播的速度;L0为试样长度;E为弹性杆的弹性模量;A为弹性杆截面积;A0为试样截面积;t为应力波脉冲持续时间。

2 含瓦斯煤动力学测试结果

为了分析轴向静载、围压、瓦斯压力和动载荷分别对含瓦斯煤动力学特征的影响，采用控制变量法分别研究了不同加载条件下的应力应变曲线、峰值强度和峰值应变与各种因素的关系，测试结果见表1。

2.1 应力-应变曲线特征分析

震动载荷作用下，不同轴向静载、围压、瓦斯压力和震动载荷下含瓦斯煤应力应变曲线分别如图3所示。不同加载条件下含瓦斯煤震动应力应变曲线基本相似，相比静态加载应力应变曲线，含瓦斯煤震动应力应变曲线没有压密期，在初始变形阶段，应力随应变线性增加，表现为弹性变形，这是因为震动载荷作用下，动载作用时间较短，煤体很快被压实并进入弹性变形期;随着应变增加，煤体应力增加到一定程度会有所放缓，之后又快速增加，呈现出“跃进”特性，这一特性可能与炭在晶体微破裂中的作用有关，类似于低碳钢[16];随着应变的进一步增加，应力达到峰值，然后降低，在最后阶段，应力应变曲线出现“回弹”现象[18]，一般认为发生回弹是峰后弹性能释放引起的，说明发生明显回弹的试样在动载作用后仍具有承载能力，在震动载荷作用下，煤样内部仅发生了微损伤而没有表现出宏观破坏。由图3(a)可知，不同轴向静载下线弹性阶段斜率受试样离散性影响较大，图3(b)和(d)显示含瓦斯煤的弹性模量随着有效围压和动载荷冲击速度增加而增大;而图3(c)显示含瓦斯煤弹性模量随瓦斯压力增加而减小。

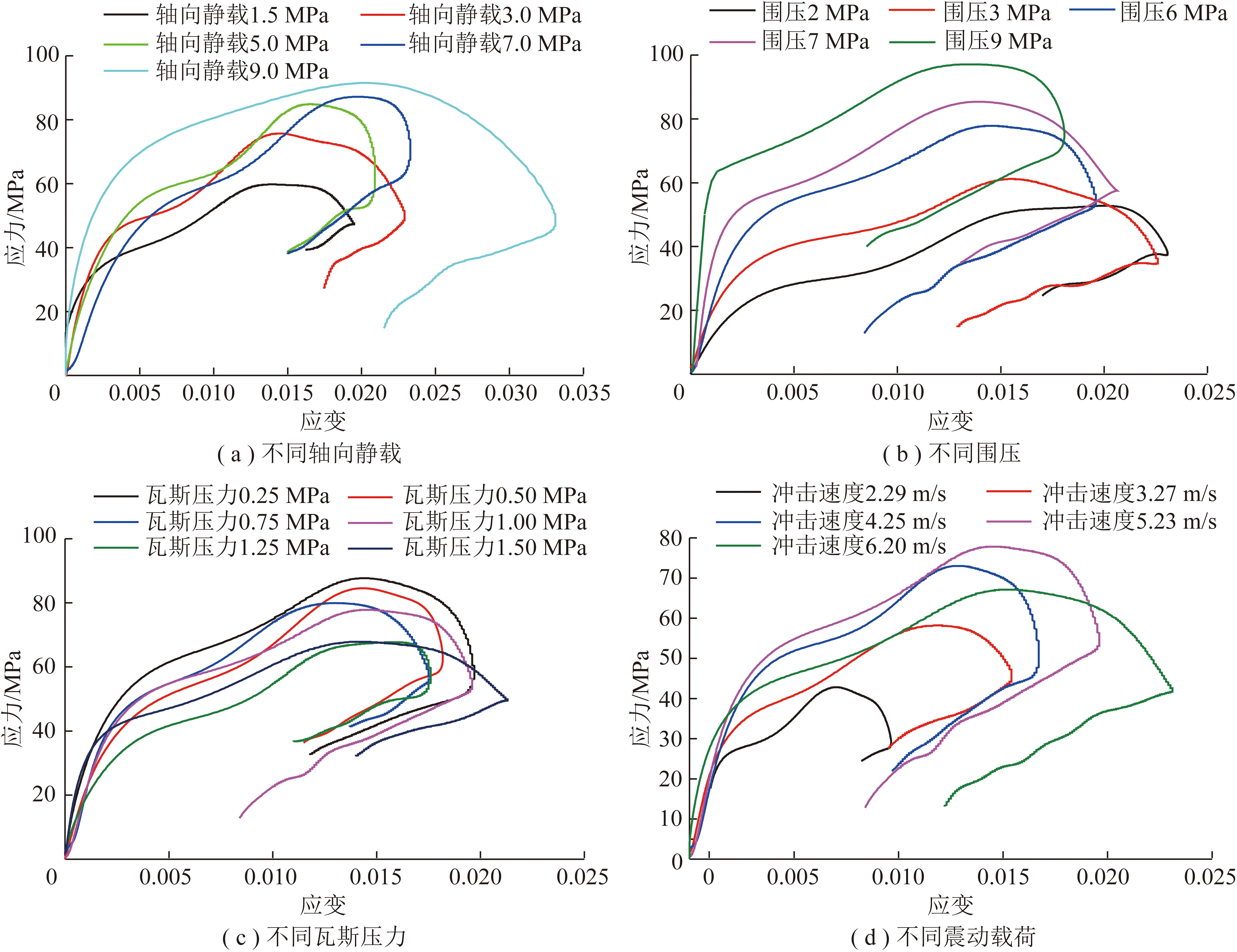
图3 不同加载条件下含瓦斯煤震动应力应变曲线Fig.3 Stress-strain curves of gas-bearing coal under different compositive loading conditions

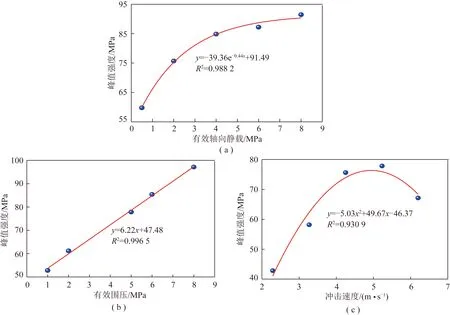
图4 含瓦斯煤动态强度与各因素的关系Fig.4 Relationships between dynamic strength of gas-bearing coal and various factors

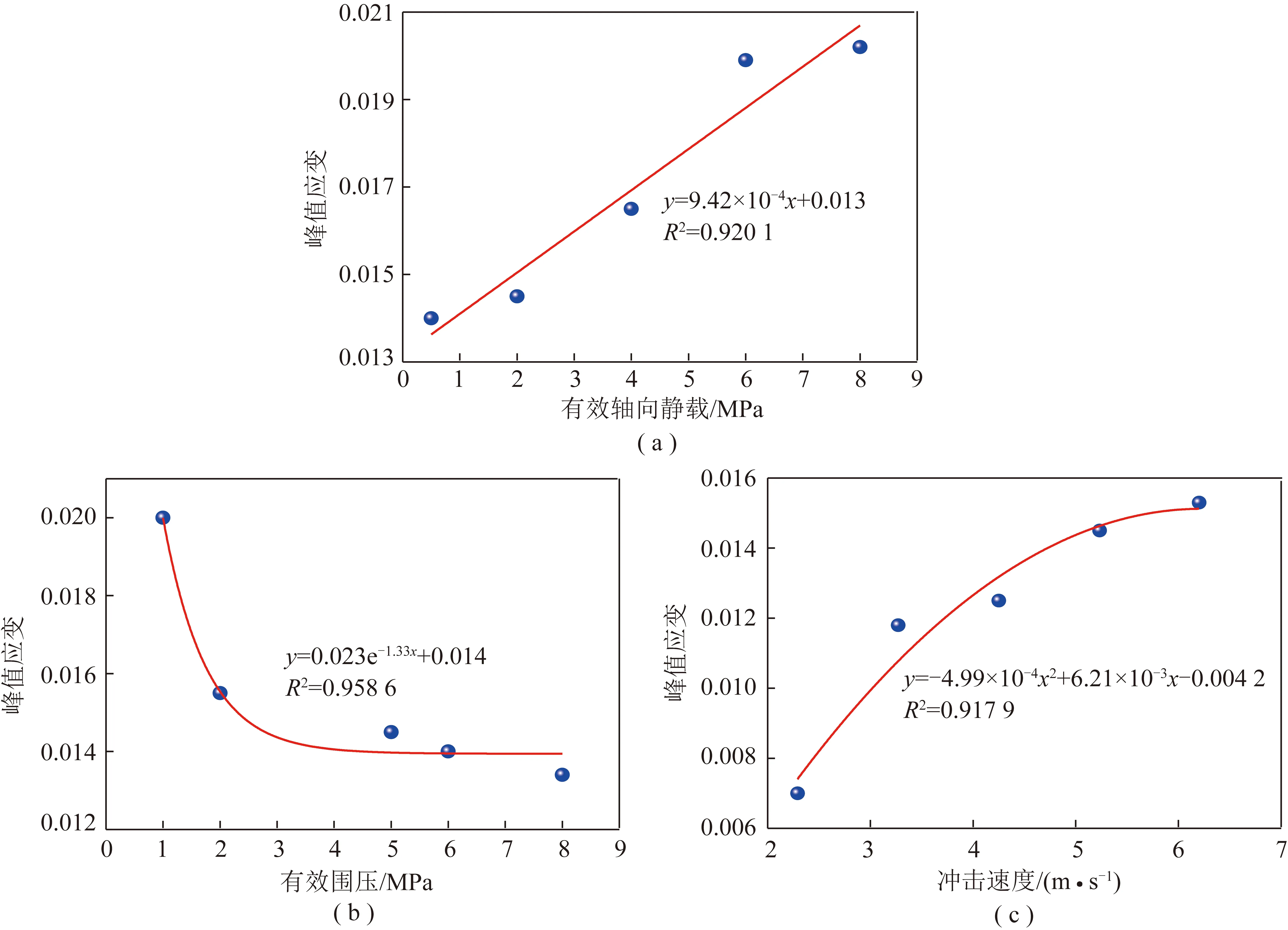
图5 震动载荷下含瓦斯煤峰值应变与各因素关系Fig.5 Relationships between peak strain of gas-bearing coal and various factors under shock load

2.2 峰值强度特征

震动载荷作用下，含瓦斯煤峰值强度与有效轴向静载、有效围压和震动载荷冲击速度的关系如图4所示。由图4(a)可知，在有效围压4 MPa和震动载荷冲击速度5.23 m/s条件下，含瓦斯煤峰值强度与有效轴向静载呈指数关系，在有效轴向静载较低阶段，峰值强度随有效轴向静载快速增加，当有效轴向静载达到一定值时，峰值强度基本维持在某个值附近，说明当动载荷较小不足使煤体破裂时，有效轴向静载有助于提高煤体抵抗外界载荷的能力;由图4(b)可知，当有效轴向静载4 MPa和震动载荷冲击速度5.23 m/s时，震动载荷作用下含瓦斯煤峰值强度随有效围压呈线性增加的趋势，拟合度高达0.996 5，这也很好地解释了上覆岩层断裂和断层滑移引起的动载多造成临空煤体和巷道变形破坏的现象，因为临空煤体和巷道都有自由面，缺失围岩的保护作用，在动载荷影响下，巷道帮部容易向自由面方向变形;由图4(c)可知，当有效轴向静载4 MPa和有效围压5 MPa时，含瓦斯煤峰值强度随冲击速度先增加后减小，证明在冲击速度较小范围内，动载强度有助于提高含瓦斯煤体的强度，表现出不易破坏的能力，当动载超过一定值时，含瓦斯煤峰值强度将随动载减小，易受外载荷扰动影响。

2.3 峰值应变特征

震动载荷作用下，含瓦斯煤峰值应变与有效轴向静载、有效围压和动载荷冲击速度的关系如图5所示。由图5(a)可知，当有效围压5 MPa和震动载荷冲击速度5.23 m/s时，含瓦斯煤震动峰值应变随有效轴向静载呈线性增加关系，拟合度大0.920 1;由图5(b)可知，当有效轴向静载5 MPa和震动载荷冲击速度5.23 m/s时，震动载荷作用下含瓦斯煤的峰值应变随着有效围压的增加呈指数衰减，拟合度为0.958 6，说明围压限制了煤体变形，有效围压越大，变形越困难，因而峰值强度所对应的煤体峰值应变也越小，类似于静态三轴加载峰值应变随轴压和围压的变化规律[24];图5(c)表明含瓦斯煤的峰值应变随冲击速度呈抛物线关系，在试验的冲击速度范围内，峰值应变随冲击速度呈增加的趋势，但增加幅度逐渐减小，即处于抛物线的上升期。

3 讨 论

3.1 含瓦斯煤峰值强度应变率效应

前述研究发现，震动载荷下含瓦斯煤动力学特征与有效轴向静载、有效围压和动载荷冲击速度具有一定的关系，但是不同条件下同一动力学参数却不具有可比性。根据一维动静载煤岩动力学特性可知，煤岩材料的应变率效应较强，应变率是表征材料变形速度的一种度量，被广泛用于材料动力学研究。因此，研究了不同有效轴向静载、有效围压和动载荷冲击速度加载条件下含瓦斯煤峰值强度的应变率效应，如图6所示。由图6(a)可知，不同有效轴向静载下，含瓦斯煤峰值强度随应变率呈指数变化，在应变率低水平阶段时，峰值强度随着应变率增加而增加，说明煤体变形速率较小时，煤体裂隙被逐渐压实以增强煤体的完整性，进而增加其峰值强度;当应变率增加到一定值时，峰值强度基本稳定在某个值附近，说明煤体变形存在一个临界应变率，超过这个值，煤体变形速率较快，煤体来不及反应就发生破坏，峰值强度将几乎不再增加，这一临界应变率可能与煤岩材料的本身特性及加载条件有关。由图6(b)可知，不同有效围压条件下的含瓦斯煤震动的峰值强度也呈现明显的应变率效应，峰值强度随应变率增加而减小，在应变率140～180 s-1，基本呈线性减小。由图6(c)可知，在应变率80～180 s-1，不同冲击速度下含瓦斯煤震动峰值强度随应变率增加而线性增加。

3.2 含瓦斯煤峰值应变应变率效应

不同有效轴向静载、有效围压和动载荷冲击速度下，含瓦斯煤峰值应变与应变率关系如图7所示。由图7(a)可知，与含瓦斯煤峰值强度随应变率变化关系类似，不同有效轴向静载下，含瓦斯煤峰值应变与应变率仍呈现指数关系，存在一个临界应变率，低于该值时，峰值应变随应变率迅速增加;超过该应变率，峰值应变逐渐趋于稳定。而图7(b)显示，不同有效围压条件下，除178.11 s-1异常点外，含瓦斯煤震动峰值应变随应变率增加而线性增加。由图7(c)可知，不同动载荷冲击速度下峰值应变随应变率增加也呈线性增加，拟合度0.952 4以上。

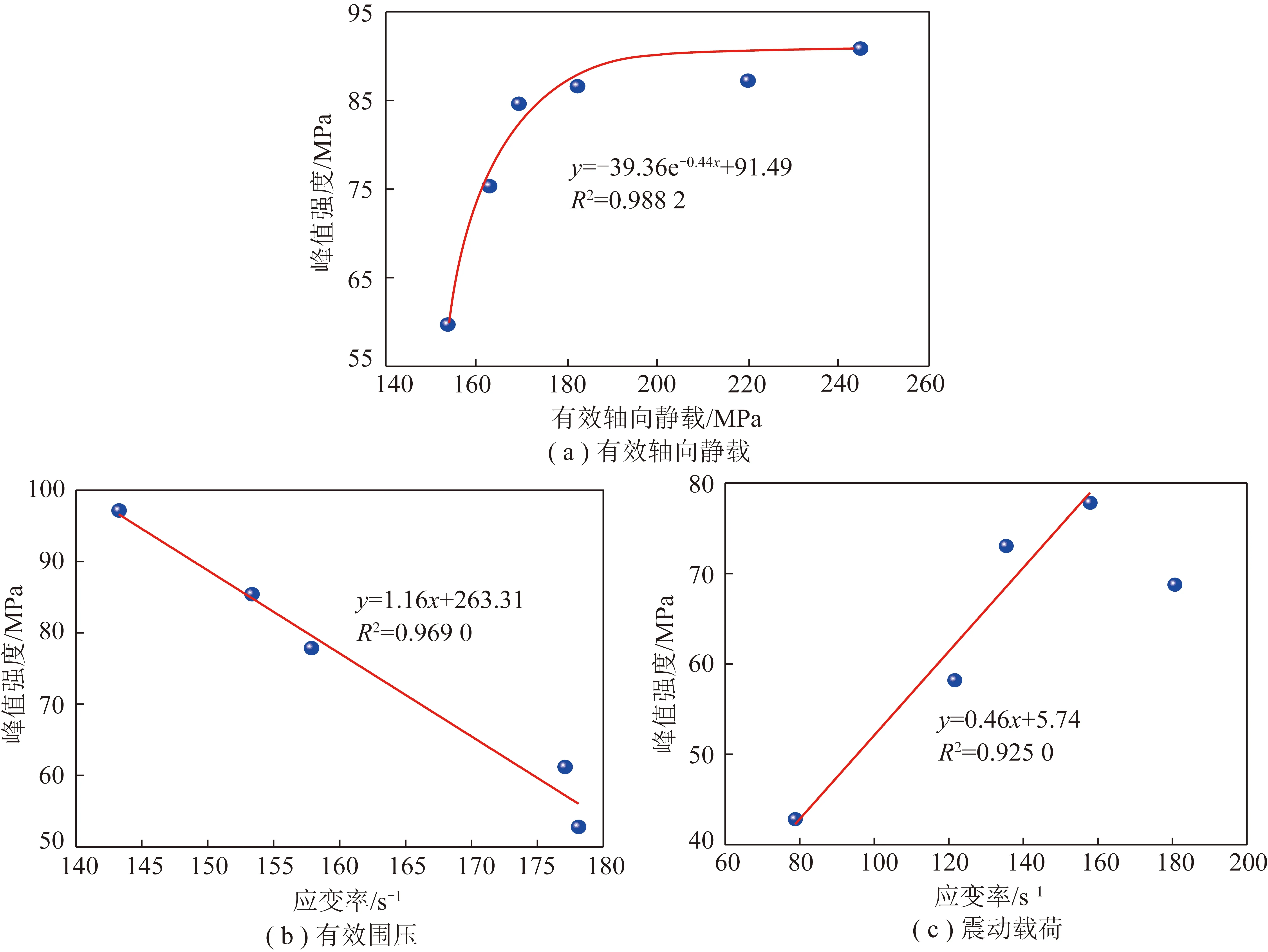
图6 含瓦斯煤峰值强度应变率效应Fig.6 Strain rate effects of gas-bearing coal peak strength

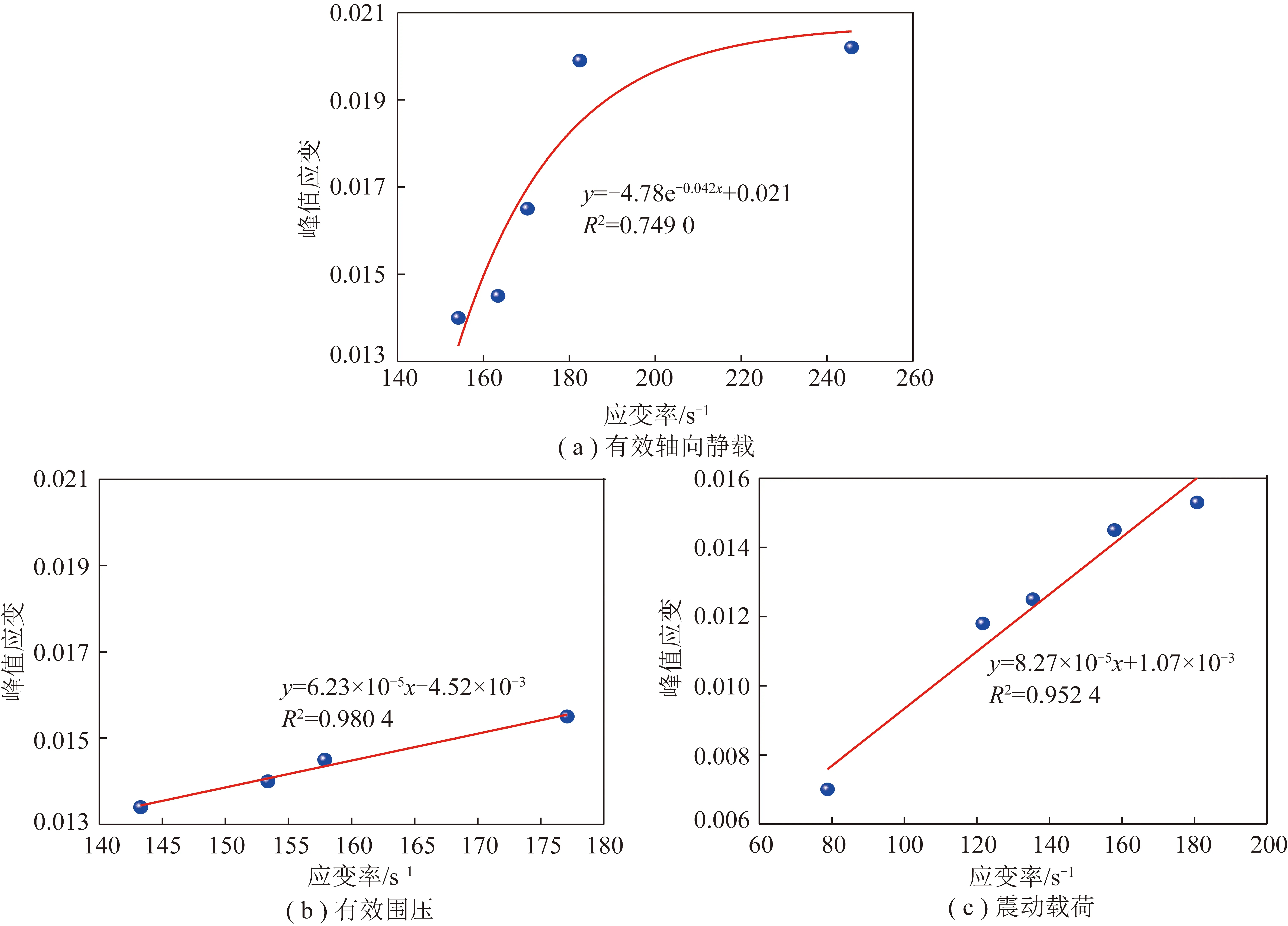
图7 含瓦斯煤峰值应变应变率效应Fig.7 Strain rate effects of gas-bearing coal peak strain

总之，震动载荷下含瓦斯煤震动应变率效应阐释了峰值强度和峰值应变与应变率的关系，使不同加载条件下的动力学指标具有可比性，即只要加载条件变化造成应变率改变，则含瓦斯煤峰值强度和峰值应变就发生相应变化。除了不同有效围压条件下峰值强度随应变率的关系，震动载荷下含瓦斯煤峰值强度和峰值应变均随着应变先增加后趋于稳定。

4 结 论

(1)震动载荷下，不同轴向静载、围压、瓦斯压力和动载荷冲击速度条件下含瓦斯煤应力应变曲线基本相似，初始加载阶段，应力随应变线性增加，表现出明显的线弹性特征;当应变增加到一定程度时，应力应变曲线呈现出“跃进”特征，与炭在晶体微破裂中作用有关;峰后弹性能释放引起应力应变曲线出现“回弹”现象。

(2)含瓦斯煤峰值强度和峰值应变随有效轴向静载、有效围压和动载荷冲击速度表现出明显的规律性。震动载荷作用下，含瓦斯煤峰值强度随有效轴向静载呈指数函数增加、随有效围压呈线性增加，随动载荷冲击速度呈先增大后减小的规律;含瓦斯煤峰值应变随有效轴向静载呈线性增加、随有效围压呈指数衰减、随动载荷冲击速度增大而增加。

(3)震动载荷下，不同加载条件下含瓦斯煤动力学指标表现出明显的应变率效应。除了不同有效围压条件下峰值强度随应变率的关系，在应变率低水平阶段，含瓦斯煤峰值强度和峰值应变均随应变率增加而增加，当应变率超过临界应变率，含瓦斯煤峰值强度和峰值应变基本稳定于某值附近。