煤燃烧成灰发射率研究进展

姚禹歌，蒋 苓，张 缦，杨海瑞，吕俊复，何 维，周 棋

(1.清华大学 能源与动力工程系，北京 100084; 2.东方锅炉股份有限公司 清洁燃烧与烟气净化四川省重点实验室，四川 自贡 643001)

煤炭是中国的基础能源。煤燃烧后其中的矿物质形成底渣和飞灰，烟气中的飞灰影响着烟气对受热面的热辐射特性。经过长期的运行，粉尘会沉积附着在水冷壁、过热器、再热器等受热面管壁表面，形成灰污层。灰污层的形成，在高温火焰和受热面之间构成了一层导热热阻，同时改变管壁表面的辐射换热特性，进而影响管内工质的换热和流动状态，对机组的经济性甚至安全性产生影响[1]。煤粉燃烧中，炉膛传热主要是以辐射换热的形式进行的[2]，火焰和烟气中粉尘的辐射特性对此有重要影响[3-4]，因此灰的发射率的确定对于煤粉锅炉的数值模拟[5-6]、设计与运行有着重要的意义[7]。

相比于燃烧优质动力煤的煤粉锅炉，循环流化床锅炉可以燃用劣质煤[8]，煤中的灰分对于循环流化床燃烧的循环物料具有至关重要的作用[9-11]，煤灰发射率也是CFB主循环回路内传热研究的重要参数[12-13]，尤其是某些事故条件下颗粒堆积向受热面的辐射，危及设备安全，因此煤灰发射率的研究具有重要意义。人们对这个问题已经有一些研究，笔者对此问题的国内外研究进行综述。

1 发射率的概念

普朗克定律描述了绝对黑体光谱辐射力Eb,λ(Τ)与波长λ和温度T的关系:

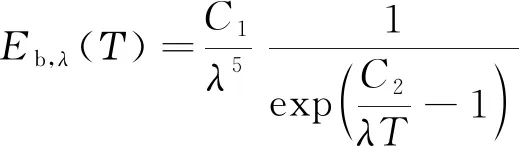
(1)

其中,C1和C2分别为普朗克第一和第二常数。根据式(1)，可以得到黑体总辐射力Eb(Τ):

(2)

式中，σb为黑体辐射常数。

实际物体的表面发射能力低于同温度下黑体的发射能力，二者的比值定义为发射率，则实际物体的光谱发射率ελ(Τ)与总发射率ε(Τ)可分别由式(3)和(4)得到：

(3)

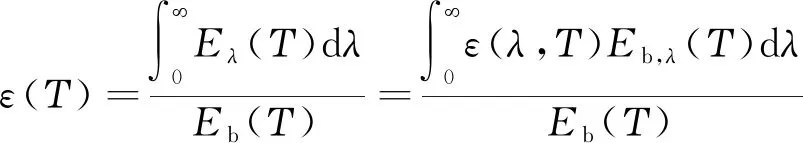
(4)

实际物体的光谱发射率ε(λ,Τ)与总发射率ε(Τ)均在0～1。

对于实际物体，所有投射到表面的热辐射能量都会被物体吸收、反射或穿透物体表面，故有

α+ρ+τ=1

(5)

式中，α为物体表面的吸收率;ρ为物体表面的反射率;τ为物体穿透率。

对于某一特定波长λ，则有

αλ+ρλ+τλ=1

(6)

又由基尔霍夫定律，对于漫射表面(如煤灰)，有

ελ=αλ=1-ρλ-τλ

(7)

2 煤灰发射率影响因素

2.1 波长λ对于煤灰光谱发射率的影响

早期学者假定煤灰属于灰体，即煤灰的光谱发射率等于总发射率，与波长无关。GOETZ等于1979年利用单色仪和红外探测仪测量4种煤灰样品在颗粒状态和熔融态的光谱发射率[14]。实验结果表明煤灰的表面光谱发射率在0.65～10 μm波长内不为常数值，有明显的变化，证明煤灰不属于灰体，不具有灰体的性质。WALL等最早利用窄角辐射计和带通滤波器测量6种煤灰颗粒样品和4种合成样品在5个不同波段内(1～2,2～3,3.0～4.3,4.3～5.8和5.8～35.0 μm)的平均发射率[15]。结果表明，对于全部样品，5.8～35.0 μm波段的平均发射率显著大于4.3～5.8 μm波段的平均发射率，4.3～5.8 μm波段的平均发射率显著大于1～2,2～3和3.0～4.3 μm波段的平均发射率，可推测随着波长的增大，煤灰光谱发射率从4.3 μm处开始将呈现显著上升的趋势，但是无法对于波长较大时光谱发射率的变化规律做出预测。

20世纪80年代末期，傅里叶变换红外光谱(FT-IR)技术已经广泛应用于光谱发射率的测量[16-18]，以此可以测量煤灰在一定波长范围内的光谱发射率。MARKHAM等最早利用FT-IR在1.6～20 μm波长范围内测量4种煤灰样品的光谱发射率[19]。图1展示了其中1种煤灰样品的光谱发射率测量结果，表明表面经过熔化过程的煤灰光谱发射率整体较高，变化范围较小，在0.8～1.0上下波动;经过烧结过程的煤灰光谱发射率可分为3段，在1.6～3.0 μm波长内波动较小，近似为常值，在3.0～8.0 μm波长内随波长的增大而明显增大，与波长近似呈线性关系，在8.0 μm左右光谱发射率达到最大值，并在8.0～20 μm内小范围上下波动;未经过烧结或熔化过程的煤灰颗粒与经过烧结过程的煤灰光谱发射率变化规律相似，但是未经过烧结或熔化过程的煤灰颗粒的光谱发射率数值较低，在3.0～8.0 μm波长内的增长更加迅速。煤灰颗粒光谱发射率与波长呈现显著的相关性。

图1 一种煤灰样品光谱发射率的测量结果[19]Fig.1 Measured spectral emittance of a coal ash sample[19]

此后，很多研究也利用FT-IR技术测量不同形态下的煤灰样品或者人工合成灰的光谱发射率，得到与图1所示结果相似的3段变化规律[20-24]。同时，BOHNES等[23]和SALJNIKOV等[24]发现，在低于3 μm时(对应图1中第1段)光谱发射率也可以随波长增大呈现不同的变化规律(增大、不变、下降)，变化规律的差异与煤灰样品的成分和表面温度有关。

2.2 表面温度T对于煤灰发射率的影响

如前所述，煤灰不是灰体，根据式(1)～(4)，其表面发射率与表面温度相关。MULCAHY等最早在550～1 650 K测量了褐煤煤灰样品在总半球发射率[25-26]。

如图2所示，从低温开始加热煤灰，随着样品表面温度的上升，煤灰的总发射率降低，到900 ℃左右，发射率下降缓慢，近似不变;随后加热至1 000 ℃左右，发射率开始随温度上升而增大，直至熔化。冷却过程中，从温度最高点开始，发射率始终随着温度的降低而减小，并且冷却过程的发射率变化曲线始终位于加热过程的发射率变化曲线(A段)之上。表面经过熔化过程煤灰的降温曲线(C段)位置经过烧结的煤灰的降温曲线(B段)之上，该研究同样测量了波长0.9 μm的光谱发射率，所得曲线与总发射率有相同的变化趋势。其余不同学者的实验结果也呈现了相似的变化规律[15,27-28]。

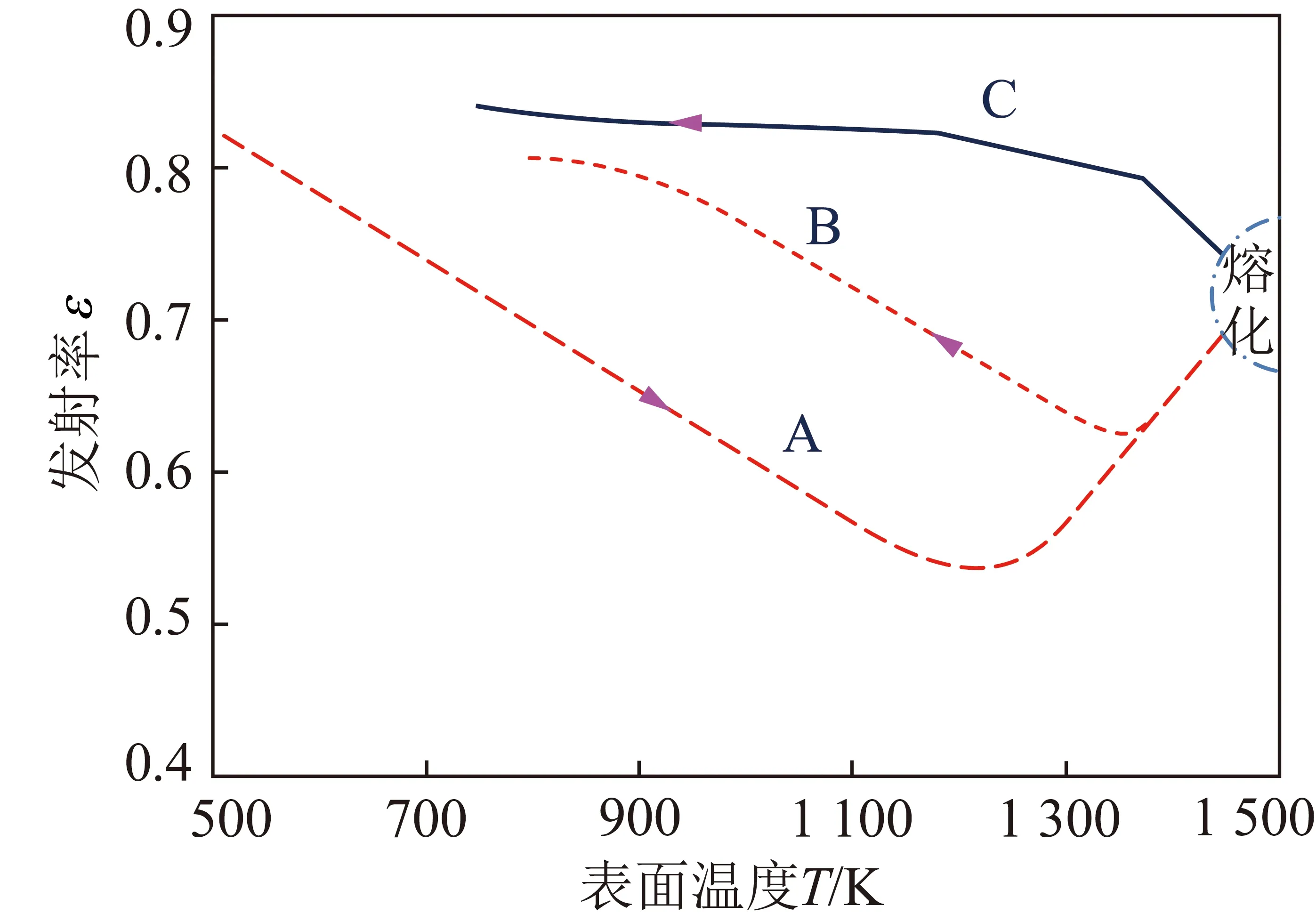
图2 表面温度对于一种煤灰总半球发射率的影响[25]Fig.2 Effect of surface temperature on total hemisp- herical emittance of a coal ash sample[25]

温度同样对于光谱发射率产生影响。如图3所示，BOHNES等的实验结果表明在波长1.0～5.0 μm，煤灰样品的光谱发射率随着温度的上升而增大，增大量较小，在5.0～15.0 μm光谱发射率与温度没有显著的相关性，整体来看温度变化对于光谱发射率的改变较小[23]。SALJNIKOV等的实验结果表明，对于部分煤灰样品，在波长1.0～5.0 μm区域内，随着温度的升高，光谱发射率随波长的相关性从正相关逐渐变为负相关[24]。

根据式(1)，当煤灰发生烧结前，随着温度的升高，黑体的主要辐射区域在光谱上的相对位置几乎不变，位于1.0～3.0 μm，并且随着温度的增加，该区域的辐射能量占比显著增大。由图1，3的测量结果，煤灰光谱发射率在1.0～3.0 μm的光谱发射率相对较低，并且温度改变对于煤灰光谱发射率的影较小，因此总发射率将会随着温度的升高而降低。当温度加热至900 ℃左右时，高温使得煤灰表面发生了不可逆的物理变化，导致了温度继续升高后发射率变化趋势的改变，也使得降温过程的发射率大于升温过程。

图3 表面温度对于一种煤灰光谱发射率的影响[23]Fig.3 Effect of surface temperature on spectral emittance of a coal ash sample[23]

2.3 表面状态对于煤灰发射率的影响

随着煤灰表面温度的升高，煤灰颗粒经历烧结和熔化2个过程，这2个过程对于煤灰颗粒表面均造成了不可逆的物理变化。GREFFRATH等在500～1 100 ℃测量了3种褐煤煤灰样品的总发射率，并对于部分样品进行1 400 ℃高温加热的预处理，以改变表面状态[29]。结果表明表面经过高温处理，经历了烧结或熔化的煤灰样品具有更高的总发射率。图2中的光谱发射率也呈现了相似的规律，结合2.2节中温度变化对于光谱发射率的改变较小的结论，可以推断表面状态是煤灰光谱发射率的主要影响因素。烧结过程和熔化过程将煤灰颗粒表面变成了“玻璃状”，在该状态下煤灰表面具有更高的透射率和更低的反射率，从煤灰内层传输至表面更多的的能量。因此相比于颗粒状煤灰，经过烧结过程或熔化过程的煤灰,在同等表面温度的条件下具有更高的发射率[30-31]。

对于颗粒状煤灰，BOOW等最早测量了4组化学组成相同的合成灰在表面温度200～1 000 ℃的总发射率，样品的平均粒径在104～211 μm[32]。实验结果表明，随着粒径的增大，样品的总发射率增大，该结论也适用于其余不同种类的煤灰、合成灰与石英砂[33]。ZYGARLICKE等也报告了粒径与发射率呈正相关的规律，并发现粒径是影响煤灰发射率的主导因素[34]。GOREWODA及其同事对于煤灰颗粒化学组成中的重要含氧化合物(SiO2,Fe2O3和CaCO3等)进行了测量，发现所有样品的发射率均随粒径的增大而增大[35]。SIH等关于SiO2颗粒的测量结果也支持上述结论[36]。MULCAHY等认为烧结过程可以视作增大了煤灰表面粒径，因此增大了发射率[25-26]。

2.4 化学组成对于煤灰发射率的影响

煤灰的化学组成比较复杂，主要含有Si,Al,Fe,Ca和Mg等元素的化合物，主要以氧化物的形式存在[37-39]，其中Fe元素或Fe2O3被普遍认为是影响煤灰发射率的主要成分。BOOW等最早利用合成灰探究Fe2O3含量对于总发射率的影响，结果表明含5%Fe2O3的合成灰样品的总发射率显著高于不含Fe2O3的合成灰[32]。GREFFRATH等在煤灰样品中掺入了2%和30%的Fe2O3，结果表明含30%Fe2O3的样品总发射率显著高于含2%Fe2O3的样品[33]。MOORE等也将现场测量中次烟煤煤灰样品光谱发射率小于烟煤煤灰样品的原因归结于煤灰中Fe2O3等效质量分数的差异[40]。GOREWODA及其同事对于比例不同的SiO2和Fe2O3的混合物样品进行测量，结果表明当Fe2O3等效质量分数超过10%时，样品的总发射率随着Fe2O3等效质量分数的增大而增大，并且该实验现象在平均粒径较低的样品中更为显著，含10%Fe2O3的混合物样品与纯SiO2的总发射率几乎相等，该实验结果也表明Fe2O3等效质量分数对于煤灰发射率的影响受到煤灰粒径的影响[35]。实际上，相比于煤灰粒径，化学组成对于发射率的影响程度较小，甚至在一定条件下可以忽略[32,34]。对于Fe2O3在化学组成中主导煤灰发射率的原因，BOOW及其同事认为Fe2O3含量较高的煤灰样品具有更高的吸收能力，因此测量得到的发射率就越高。Fe2O3含量与样品的颜色有关，Fe2O3含量越高的煤灰样品，通常具有较深的红色，因此颜色较深的样品通常具有较高的发射率[32]。该研究同时也发现含有碳颗粒的合成灰样品拥有更高的发射率，这也验证了上述分析。

对于除了Fe2O3以外的其余化学组成，BOHNES等认为SiO2是决定煤灰发射率随温度改变趋势的重要成分，纯Fe2O3的发射率随温度变化反而不显著[23]。化学组成的改变也会影响着煤灰的熔融特性[41-45]，进而改变发射率随温度的变化曲线。LINKA等则发现由于煤灰中大量存在SiO2,Al2O3和MgO，因此在波长较大时煤灰光谱发射率较大;FeO(Fe2+)则对于1 μm附近的光谱发射率有重要影响[46]。

2.5 煤灰发射率影响因素分析

除了波长、表面温度、表面性质、化学组成外，颗粒孔隙率对颗粒堆积表面发射率也有重要影响[36]，SALJNIKOV等发现当灰层厚度大于1 mm时，发射率与灰层厚度无关[28]。

目前关于煤灰发射率影响因素的研究大多属于定性研究，对于影响趋势给出结论。由于煤灰种类较多，与发射率有关的影响因素也很多，因此很难进行具有普适性的定量研究，甚至会有不同的变化趋势。但是在一定实验条件下，煤灰发射率的变化规律可以为实际应用中发射率的预测提供有价值的参考。

3 煤灰发射率的预测

3.1 基于物理过程的预测

灰颗粒层可以视为不透明物体[28]:

τλ=0

(8)

因此式(7)可以写成

ελ=αλ=1-ρλ

(9)

因此通过对于物体表面反射率的分析与计算，可以得到煤灰的光谱发射率。目前对于这一问题的求解模型可以大致分为3类。在所有的求解模型中，都对于煤灰灰层做出了假设:① 煤灰颗粒尺寸一致;② 煤灰颗粒化学组成一致;③ 煤灰颗粒光学性质(复折射率)一致;④ 灰层是一个对称的无限大平壁。

第1类求解模型是MARKHAM等[19]提出的均匀表面模型:

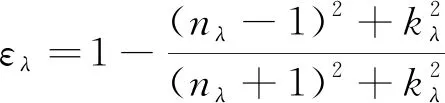
(10)

式中，n和k分别为煤灰的实折射率和吸收系数，是复折射率m=n-ik中的实部和虚部。

该模型仅适用于足够光滑的表面，BHATTACHARYA指出该模型的适用条件是h<λ/(8cosθ)，其中h为表面不规则尺寸，θ为入射角度，即煤灰颗粒粒径相比于波长要足够小，因此该模型仅适用于经过熔化过程的煤灰[47]。MARKHAM等对于该模型的计算结果也表明，该模型在预测表面经过熔化过程的煤灰时具有较好的准确性，然而无法应用于颗粒状煤灰的光谱发射率预测[19]，但是该模型可以给出煤灰光谱发射率的上限[48]。

第2类模型是BHATTACHARYA提出的基于煤粉锅炉换热器灰渣的辐射传递模型。该模型对于炉膛内部从火焰到换热器表面灰渣和换热器管壁的辐射传递过程，考虑了到飞灰对于这一过程的影响[47,49]。该模型中，辐射强度在灰层内部一维传递，满足

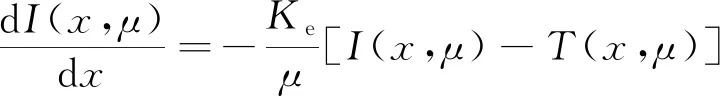
(11)

式中，μ为入射角的余弦值，即μ=cosθ;I(x,μ)为某一位置某一方向的辐射强度，如图4所示。Ke为消光系数;T(x,μ)为某一位置某一方向的能量参数，与I(x,μ)、黑体辐射和散射有关参数等有关。

该模型所预测的光谱发射率与前述的煤灰颗粒光谱发射率测量结果的趋势相同。该模型对于总半球发射率的计算结果可以正确地预测煤灰颗粒粒径和Fe的含量对于总发射率的影响趋势。同时该模型指出光学性质(复折射率)对于发射率有显著影响。

第3类模型是基于BOHREN提出的双通量模型进行反射率或光谱发射率的求解[50]。该模型将灰层中的辐射视作两个相对的半球辐射，其辐射强度只有正负两个方向，在这两个方向的半球内辐射具有各向同性。该模型可以适用于三维空间的建模。最终求得光谱发射率:

(12)

其中，ω0为灰颗粒散射率;g为非平衡因子，二者的求解均与MIE散射理论有关。刘东等采用这一类模型，并进行了相关散射修正，得到相比于BHATTACHARYA的模型更加准确的预测结果[51]。文献[48]是对于散射的进一步修正。

以上总结的基于物理过程对于煤灰发射率进行建模和预测的过程，均涉及散射理论及其计算，过程较为复杂[52]，上述模型难以应用于实际生产过程中;同时上述模型对于复折射率中n和k的选取也受到煤灰粒径、孔隙率和化学组成等很多因素的影响[53-54]，给模型的使用带来一定的困难。

3.2 基于实验结果的预测

为了便于实际应用，很多学者也基于实验结果给出了不同的预测方式和经验或半经验公式。

MULCAHY等发现波长为0.9 μm时的光谱发射率与总发射率有相同的变化趋势，但数值稍微小于总发射率[25-26]。变化趋势的相同预示着在一些特定情境下可用某一波长下的光谱发射率来代替总发射率。WALL等提出利用有限波段内的平均发射率对总发射率εt进行估算[15]，并将式(4)改写成

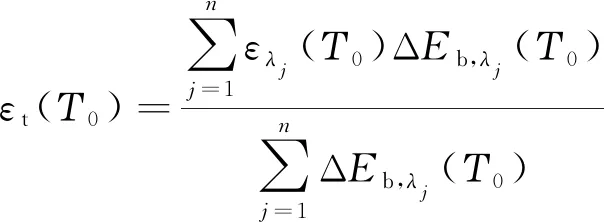
(13)

其中，λj选取为该波段内的平均值，即

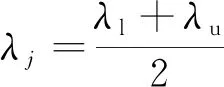
(14)

式中，λl和λu分别为该波段内的最小波长和最大波长。

BOOW及其同事针对粒径和含Fe量(颜色)的影响，给出了在表面温度为500 ℃时半球发射率εh与粒径d的关系式[32]，该关联式适用于7～420 μm粒径。对于不含Fe(无颜色)的煤灰:

εh=0.25lgd+0.13

(15)

对于含Fe(有颜色)的煤灰:

εh=0.30lgd+0.16

(16)

该研究也发现半球发射率εh与煤灰导热系数k的自然对数值lnk近似呈线形关系，在表面温度为500 ℃时给出预测公式:

εh=0.51lgk+2.44

(17)

其相关系数可达0.94。

ZBOGAR等给出了如下的预测方法[55]:当温度低于烧结温度时，可以根据BOOW等的实验数据建立发射率与温度的线性关系式[32];当温度高于熔化温度，法向发射率可以选取为0.955，对于半球发射率可以用WALL等提出的εh=0.92εn来确定[15];当温度处于烧结温度和熔化温度之间时，可以根据BOOW等的实验数据建立发射率与温度的线性关系式[32];对于含铁量的影响，可以参照ε(5%Fe2O3)/ε(1%Fe2O3)为1.12的经验值。

WALL等指出[1]，BOOW等的实验数据[32]与实际煤粉锅炉中灰渣发射率相比偏低，这是由于灰渣附着在换热器管壁表面，灰渣表面会存在一定的曲率而并非平面。该研究给出了实际锅炉中灰渣发射率εe与实验得到的平面半球发射率εh的经验关联式:

(18)

SIH和BARLOW[36]认为，煤灰表面发射率ε可以视作颗粒固体表面发射率εS和煤灰颗粒间空腔的发射率εH的加权平均数:

ε=AHεH+(1-AH)εS

(19)

其中，εH可以表达为εS和煤灰颗粒孔隙率φ的函数:

(20)

(21)

AH为空腔的面积占比，可表达为φ的函数:

(22)

由式(20)和式(21)可以看出，εH显著大于εS，并且在φ很小的时候可以接近1。又结合式(22)可知表面发射率ε可以写成φ的函数，进而通过孔隙率的测定即可得到表面发射率。

上述预测方法均针对总发射率。对于光谱发射率，SHIMOGORI等将光谱发射率分为两段[56]，第1段在波长0～8 μm单调增加:

ελ=k1λ2(k2-λ)+k3

(23)

在8 μm(λmax)以上光谱发射率为常数εmax=0.85。

在式(23)中:

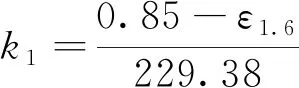
(24)

k2=1.5λmax

(25)

k3=1.12ε1.6-0.10

(26)

其中,ε1.6为波长1.6 μm的光谱发射率，可以根据Fe2O3含量CFe2O3预测:

ε1.6=(0.164+0.25lgCFe2O3)×

(0.001 76T-1.065)

(27)

其中,温度T的单位为K。该预测模型与对于大量实验数据的预测误差在±20%以内。

TSUDA等将光谱发射率分为3段[57]，当2 μm ≤λ<4 μm时，有

ελ=A+Bλ

(28)

当4 μm ≤λ≤ 8 μm时，有

ελ=E0+E1(λ-4)+E2(λ-4)2+E3(λ-4)3

(29)

当λ>8 μm时，有

ελ=C+Dλ

(30)

该模型中A，B，C和D为根据实验值确定的参数，E0，E1，E2和E3为与A,B,C和D有关的参数。

SALJNIKOV等假设半球发射率等于法向发射率，结合2.5～25 μm波长的管沟发射率实验数据，给出以下的光谱发射率预测式[28]:

(31)

其中，εmax，εmin和p可以写成与温度T有关的函数;λm为实验数据中光谱发射率上升段的中点波长，λm的选取对于光谱发射率的预测影响不显著。该研究中提供了4种煤灰样品εmax，εmin和p与温度T的拟合公式和λm的取值。

上述基于实验数据给出的预测方法或经验公式在实际应用中比较简便，往往通过1个或少量几个煤灰的特性参数就可以推出发射率的预测值。然而由于煤灰种类较多，其发射率的影响因素也很多，因此绝大多数经验公式的适用范围较小，并依赖于一定数量的实验测量值。

4 结 语

煤灰发射率是探究煤燃烧形成的灰颗粒以及炉内传热的关键参数，对于煤粉锅炉和CFB锅炉的安全运行均有重要的意义。笔者对数十年来国内外学者对于煤灰发射率的研究进行综述。基于不同学者的实验研究，总结了煤灰发射率的影响因素，包括波长，温度，表面状态，化学组成等。煤灰不能视为灰体，其光谱发射率随波长变化明显。温度和表面状态对于煤灰发射率的影响相比于化学组成更为显著，Fe元素是影响煤灰发射率的主要化学元素。基于影响因素的实验探究大多只能给出定性的结论。也对于不同学者提出的发射率的预测模型进行综述。基于物理过程建立的模型涉及散射理论相关的计算过程，应用较为复杂。基于实验结果的经验模型将发射率表示为1个或少量几个影响因素的函数，拥有较为简便的表达形式。然而经验模型往往具有严格的限制条件，应用范围较小，并且依赖于实验数据。因此对于煤灰发射率的实际测量是必要的，然而电站锅炉现场测量往往较为困难，不易实现。

目前有关于煤灰发射率的探究还难以给出具有普适性的定量的结论，也几乎没有同时涵盖多种主要影响因素的经验模型，目前已有的测量数据也不足以填补上述研究的空白。研究现状表明，对于不同种类煤灰发射率以及煤灰主要组成成分发射率的数据库的建立将对于实际应用有很大的帮助。因此，在未来的研究中，不同种煤灰在不同实验条件下测量数据的收集，整理与完善是非常重要的。测量数据的不断补充，会给实际应用中发射率的选取提供更多的参考信息，也有助于煤灰发射率预测模型的进一步完善。