基于大数据挖掘的深土井壁极限承载力模糊随机模型
2020-04-23姚亚锋荣传新姚直书薛维培
姚亚锋,程 桦,荣传新,姚直书,薛维培
(1.安徽理工大学 安全科学与工程博士后科研流动站,安徽 淮南 232001; 2.南通职业大学 建筑工程学院,江苏 南通 226001; 3.安徽大学 资源与环境工程学院,安徽 合肥 230022; 4.安徽理工大学 土木建筑学院,安徽 淮南 232001)
随着煤炭资源的不断开发,新井建设时穿过的表土层将越来越厚,井壁所承受的外荷载明显增加且伴随不确定性[1-4],导致井壁安全面临着巨大考验。为有效抵御复杂多变的外荷载作用,对于深厚冲积层中的井筒支护,通常采用高强钢筋混凝土井壁结构。
前期理论分析和试验结果表明,虽然高强混凝土可提高井壁强度,但随着强度等级的提高,其脆性也相应增大,反而导致井壁的可靠性下降。考虑到建井速度和造价,井壁厚度设计也不宜过大。因此,设计安全可靠的井壁结构参数及计算准确的井壁极限承载力已成为建井界亟待解决的焦点问题。
国内外学者在这方面研究已取得一些成果:徐栓强等[5]采用双剪统一准则进行井筒的安定性分析,得出应力和极限承载力的一致解析解。姚直书等[6]针对双层钢板高强混凝土复合井壁的强度进行了承载力试验和数值模拟,获其井壁结构强度的计算公式。梁化强等[7]利用弹性理论将井壁承载力问题变换为空间轴对称问题,得出约束内壁前后井壁的应力解。姚直书等[8]经过理论研究和模型试验,分析该复合井壁结构的力学特性和极限承载力大小,根据试验结果和公式推导获得承载力的解析表达式。但这些分析求解尚未综合考虑深厚冲积层下复杂多变的岩土环境和自身材料参数的不确定性,在实际使用中会有一定的局限性。
笔者基于改进的大数据挖掘算法,以两淮矿区现有深厚冲积层高强钢筋混凝土井壁结构参数和大量的试验数据为依据,分析井壁结构材料、几何参数和计算模式等因素的不确定分布规律,进而建立大数据挖掘井壁极限承载力的模糊随机模型。
1 高强钢筋混凝土井壁模型试验
1.1 试验装置及方法
进行高强钢筋混凝土井壁的原型破坏性试验的难度较大,因此根据相似性理论和弹性力学方程,常采用缩小尺寸的井壁结构模型进行相应的试验研究。满足的相似性[9-11]条件为
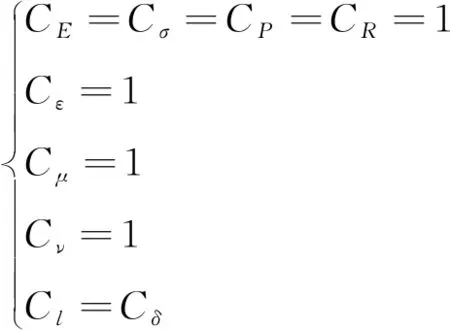
(1)
其中,CE为弹性模量相似常数;Cσ为应力相似常数;CP为荷载相似常数;CR为强度相似常数;Cε为应变相似常数;Cμ为配筋率相似常数;Cν为泊松比相似常数;Cl为几何相似常数;Cδ为位移相似常数。
为确保满足相似性,试验前需采用精密模具浇注井壁模型。加工完成后进行养护,再在磨床上抛光,保证模型表面光滑。将模型同一水平内外表面及钢筋网内外排粘贴若干应变片,用于记录钢筋混凝土应变值(图1(a)),在加载台座上下端面各设置一道橡胶圈密封,保证模型在径向的自由滑动。
试验过程中,采用如图1(b)的专门高强液压加载装置,由高压油泵施加水平油压模拟横向均匀地压作用,竖向采用刚度极大的螺栓和盖板紧紧约束,确保井壁模型始终处于平面应变状态。预加载3次之后,进行分类分级加载,每30 s 加载0.5 MPa,然后稳压1~2 min 再继续加载。最后以 2 MPa 为一级记录每级荷载作用下钢筋混凝土应变值,通过传感器对荷载进行实时监控直至井壁破裂,确保试验结果和误差在规定范围内。
1.2 试验结果
以两淮矿区的潘北矿风井和口孜东矿主井井壁为原型,按上述试验方法浇筑钢筋混凝土井壁模型,采用直径6 mm的冷轧钢筋,混凝土配合比见表1。利用相似性原理对井壁模型进行极限承载力试验,结果见表2。
1.3 结果分析
试验结果发现,混凝土抗压强度、厚径比(井壁厚度与内半径之比)和配筋率对井壁极限承载力均起不同程度的影响作用。假定其中两个参量不变,继续进行模型试验,可得极限承载力与抗压强度、厚径比和配筋率的曲线关系,如图2所示。
表1 井壁模型混凝土配合比
Table 1 Concrete proportion of shaft lining models
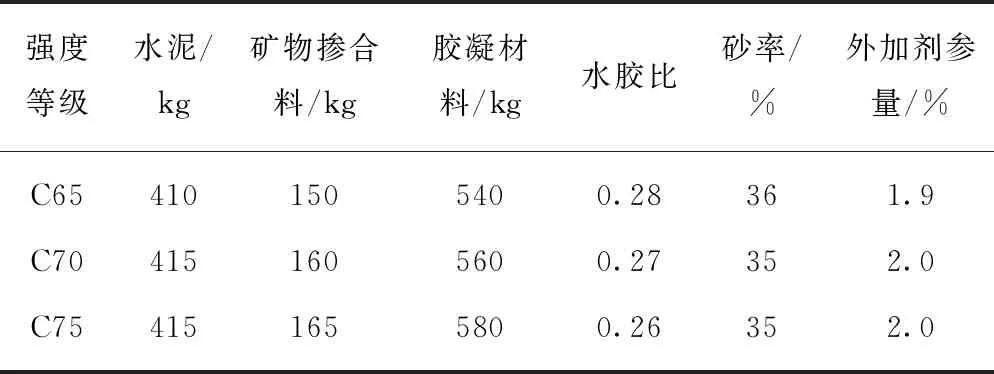
强度等级水泥/kg矿物掺合料/kg胶凝材料/kg水胶比砂率/%外加剂参量/%C654101505400.28361.9C704151605600.27352.0C754151655800.26352.0
表2 井壁模型极限承载力试验结果
Table 2 Test results of shaft lining models loading capacities
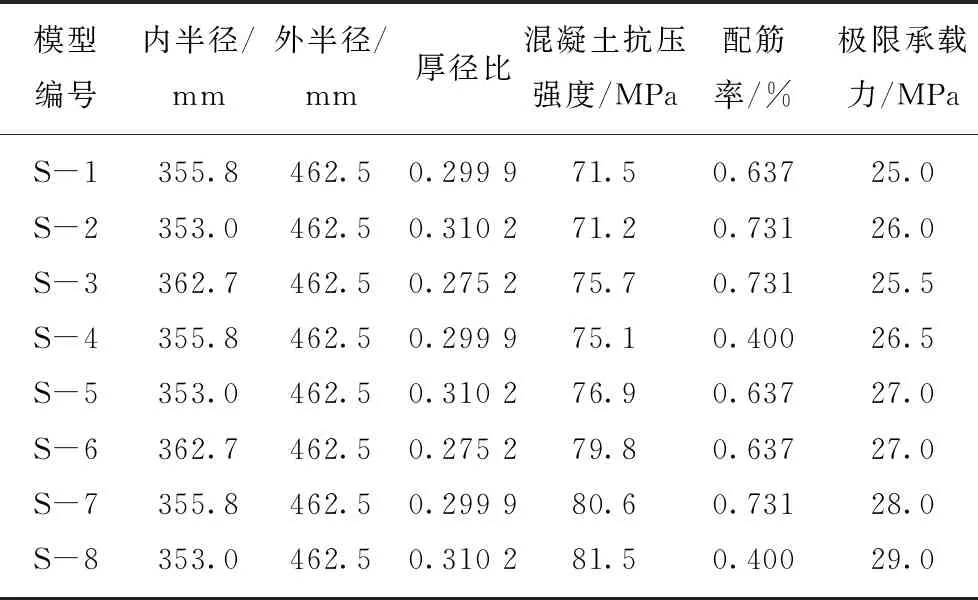
模型编号内半径/mm外半径/mm厚径比混凝土抗压强度/MPa配筋率/%极限承载力/MPaS-1355.8462.50.299 971.50.63725.0S-2353.0462.50.310 271.20.73126.0S-3362.7462.50.275 275.70.73125.5S-4355.8462.50.299 975.10.40026.5S-5353.0462.50.310 276.90.63727.0S-6362.7462.50.275 279.80.63727.0S-7355.8462.50.299 980.60.73128.0S-8353.0462.50.310 281.50.40029.0
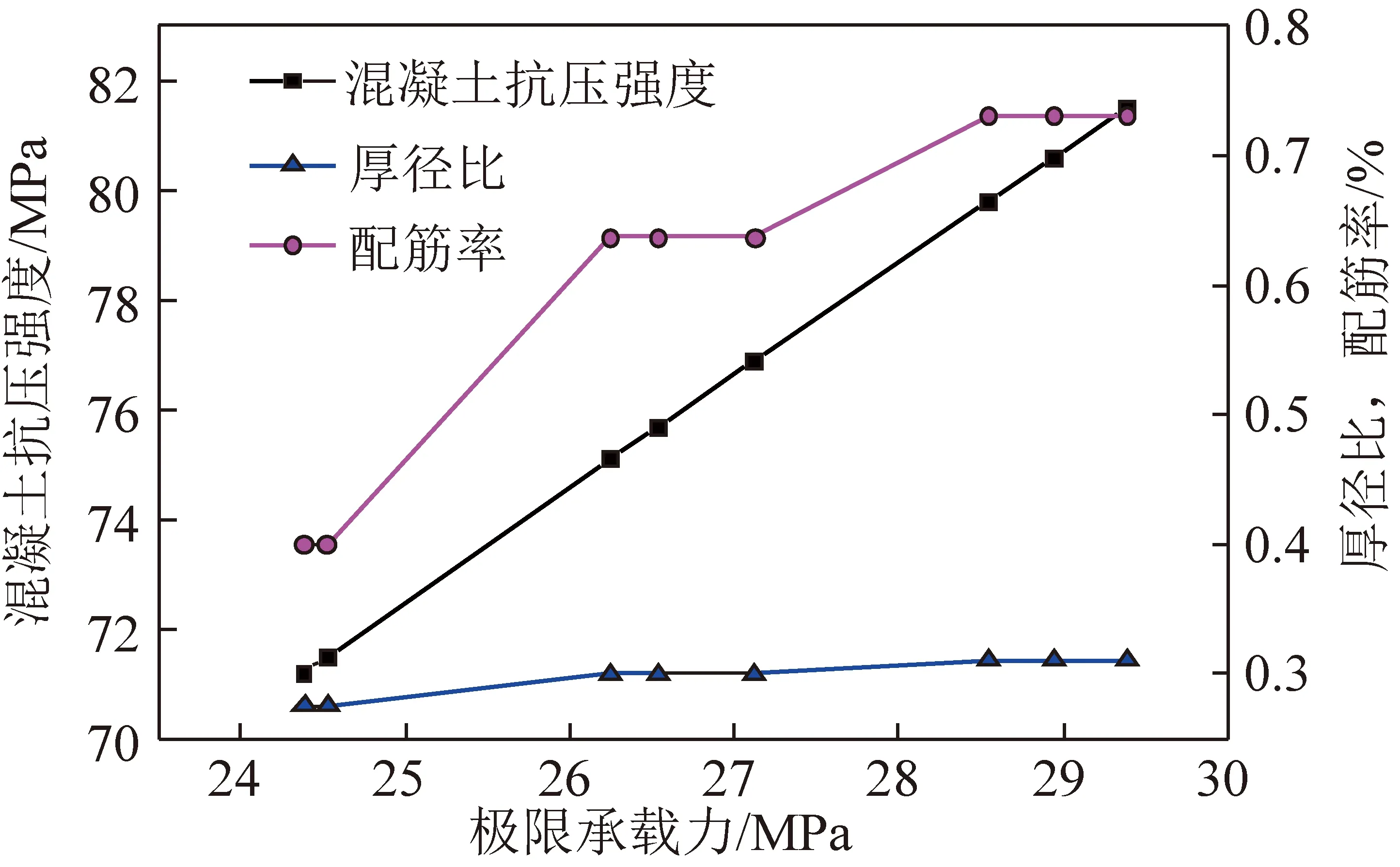
图2 井壁结构参数关系曲线Fig.2 Relationship curves between structural parameters of shaft lining
曲线表明,混凝土抗压强度对提高井壁承载力最为显著,井壁混凝土强度上升0.4%,极限承载力就能增加1 MPa左右;而配筋率对承载力影响最弱,配筋率提高15%,则井壁极限承载力才能提高1 MPa左右。在试验过程中,尽管各参数表现出大致的影响规律,但同时考虑到深厚冲积层施工过程中的模糊随机性,为经济合理地设计井壁结构和计算极限承载力指导工程实践,需首先对各因素(参数)进行模糊随机分析。
2 极限承载力影响因素模糊随机分析
井壁的极限承载力是指井筒壁能承受或抵抗外荷载的最大能力,它是进行井壁结构可靠性分析及概率极限状态设计的基础,也是施工安全的依据。
通过大量的井壁模型试验和工程实践发现,高强钢筋混凝土井壁极限承载力与混凝土抗压强度、厚径比和配筋率等因素有关。具体工程中,由于井壁结构材料的不确定性、几何参数的不确定性和计算模式的不确定性,导致深厚冲积层中井壁的极限承载力同样具有模糊随机特性。
2.1 结构材料的模糊随机分布
根据因素分析,钢筋混凝土井壁结构材料的不确定性主要来自混凝土抗压强度的模糊随机性。混凝土轴心抗压强度是指按标准方法制作的150 mm×150 mm×300 mm棱柱体试件能抵抗外部的压强值[12]。假设井壁结构材料的不定性用模糊随机变量ΘK表示,即

(1)
式中,Ks,Kb分别为高强混凝土轴心抗压强度的实测值和标准值。
通过对两淮矿区冻结井筒中高强混凝土的强度进行调研,整理并收集了大量的高强混凝土预留试块强度数据,将一些非标准试块标准化处理后进行测量和统计,得到不同强度等级高强混凝土轴心抗压强度的模糊随机分布规律,见表3。
表3 高强混凝土抗压强度模糊随机分布
Table 3 Fuzzy random distribution of high strengthconcrete compressive strength

参量混凝土等级C60C65C70C75C80均值μK/MPa38.541.544.547.450.2标准差σK3.980 95.295 43.244 14.104 04.779 0变异系数δK0.103 40.127 60.072 90.086 50.095 2
由此推断变量ΘK的分布特征为
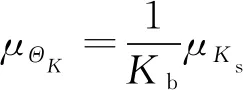
(3)
δΘK=δKs
(4)
式中,μΘK,μKs分别为ΘK,Ks的均值;δΘK,δKs分别为ΘK,Ks的变异系数。
2.2 几何参数的模糊随机分布
钢筋混凝土井壁结构几何参数的不确定性主要来自井壁施工偏差引起的厚径比和配筋率的模糊随机性[13]。厚径比是井筒几何特征的参数,指井壁厚度与内半径之比;而配筋率是影响构件受力特征的参数,指钢筋混凝土构件中纵向受力钢筋的面积与构件的有效面积之比。假设几何参数的总体不定性用模糊随机变量ΘG表示,即
ΘG=ΘMΘN
(5)
式中,ΘM,ΘN分别为厚径比的不定性和配筋率的不定性。根据数字特征的基本性质,可得
μΘG=μΘMμΘN
(6)
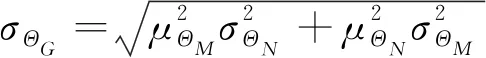
(7)
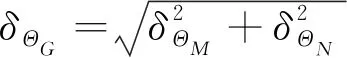
(8)
式中,μΘG,μΘM,μΘN分别为ΘG,ΘM,ΘN的均值;σΘG,σΘM,σΘN分别为ΘG,ΘM,ΘN的标准差;δΘG,δΘM,δΘN分别为ΘG,ΘM,ΘN的变异系数。
分析井壁结构几何参数不定性产生的原因,厚径比不定性模糊随机变量ΘM及分布可表示为

(9)
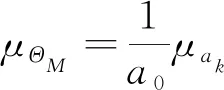
(10)

(11)
δΘM=δak
(12)
式中,ak,a0分别为井壁结构厚径比的实测值与设计值;μΘM,μak分别为ΘM,ak的均值;σΘM,σak分别为ΘM,ak的标准差;δΘM,δak分别为ΘM,ak的变异系数。
同样,配筋率不定性模糊随机变量ΘN及分布可表示为

(13)
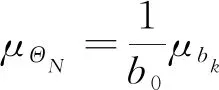
(14)

(15)
δΘN=δbk
(16)
式中,bk,b0分别为井壁结构配筋率的实际值与设计值;μΘN,μbk分别为ΘN,bk的均值;σΘN,σbk分别为ΘN,bk的标准差;δΘN,δbk分别为ΘN,bk的变异系数。
将式(9)~(16)代入式(5)~(7)可得几何参数总体不定性的模糊随机分布:

(17)
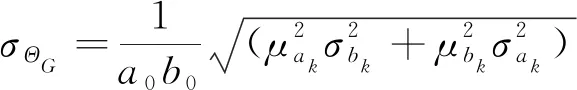
(18)
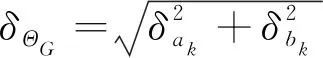
(19)
通过对两淮矿区冻结井筒中厚径比和配筋率进行调研,整理并收集了几十组井筒的几何参数,并在不同层位取样,样本达数百个。分析得到深厚冲积层高强钢筋混凝土井壁结构几何参数中的厚径比和配筋率不定性的模糊随机分布规律,见表4。
表4 厚径比与配筋率不定性的模糊随机分布
Table 4 Fuzzy random distribution of uncertainty aboutratio of lining thickness to inner radius andreinforcement ratio

几何参数厚径比不定性ΘM配筋率不定性ΘN均值μ1.033 41.040 7标准差σ0.254 00.074 7变异系数δ0.245 80.071 8
2.3 计算模式的模糊随机分布
计算模式的不确定性主要指在计算钢筋混凝土井壁极限承载力时由于采用的公式和假设不精确而引起的模糊随机性,可通过与试验测量值或规范模式的结果对比来反映其分布。假设钢筋混凝土井壁极限承载力计算模式的不定性用模糊随机变量ΘR表示:
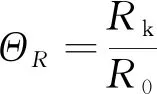
(20)
式中,Rk为钢筋混凝土井壁结构极限承载力的实际值(试验值);R0为相应经验公式的计算值。
根据安徽理工大学地下结构所钢筋混凝土井壁模型试验多年研究结果:在极限状态下,如果忽略配筋率对井壁极限承载能力的影响,则井壁截面上的切向载荷主要同混凝土抗压强度与井筒厚径比有关[14-16]。由大量试验数据回归得到井壁极限承载力的公式,即
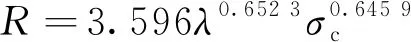
(21)
式中,R为井壁极限承载力;σc为混凝土轴心抗压强度;λ为井筒厚径比。
式(21)是假设在均布荷载作用下,忽略配筋率时井壁极限承载能力的计算公式。因此,R0可表示为

(22)
若考虑配筋率,假设井壁环向截面上的应力是均匀分布的,由轴对称平衡条件可得
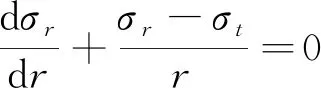
(23)
式中,σr为沿径向分布的应力;σt为沿环向分布的应力;r为井筒的半径。

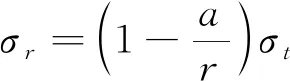
(24)
考虑到井壁内混凝土强度随径向应力的增大而提高,根据混凝土强度试验资料,井壁内混凝土强度条件可表示为
σt-κσr=σc
(25)
联立式(22)和(23),考虑配筋率的影响,经过整理可得钢筋混凝土井壁极限承载能力的计算公式为
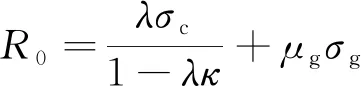
(26)
式中,κ为混凝土强度系数;μg为井筒环向配筋率;σg为井壁内钢筋的屈服强度。
将式(22)和(26)不同模式下的钢筋混凝土井壁极限承载力计算值与实测值对比,按式(20)得计算模式不定性的模糊随机分布,见表5。
表5 极限承载力计算模式不定性的模糊随机分布
Table 5 Fuzzy random distribution of uncertainty aboutcalculation mode of ultimate bearing capacity

计算模式不定性均值μΘR标准差σΘR变异系数δΘRΘR0.850 30.216 70.254 8
3 极限承载力的模糊随机分布
在大数据基础上,综合考虑井壁结构材料、几何参数和计算模式的不确定性影响,分析钢筋混凝土井壁极限承载力的模糊随机分布特性[17-18]。根据式(20)可得
Rk=ΘRR0=ΘRR[(ΘKi,fΘKi)(ΘGi,fΘGi)]
(i=1,2,3,…,n)
(27)
式中,Rk,R0分别为极限承载力的实际值和经验公式的计算值;ΘR为计算模式不定系数;ΘKi,fΘKi分别为井壁结构第i种材料相应性能的变量和标准值;ΘGi,fΘGi分别为井壁结构第i种几何参数的变量和标准值。
由于式(26)的计算结果更加接近实际值,故将其代入式(26)有
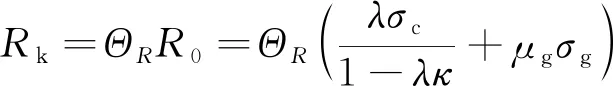
(28)
将R0按泰勒级数进行展开,可得其均值、标准差和变异系数:
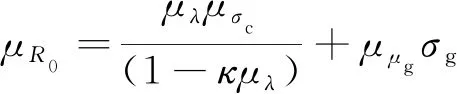
(29)
σR0=
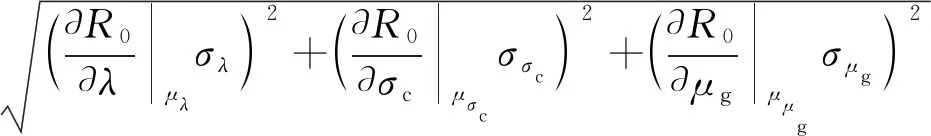
(30)
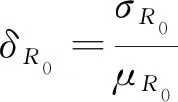
(31)
式中,μR0,μλ,μσc,μμg分别为R0,λ,σc,μg的均值;σR0,σλ,σσc,σμg分别为R0,λ,σc,μg的标准差。
经过模糊随机分析,钢筋混凝土井壁极限承载力实际值Rk的均值、标准差和变异系数分别为

(32)
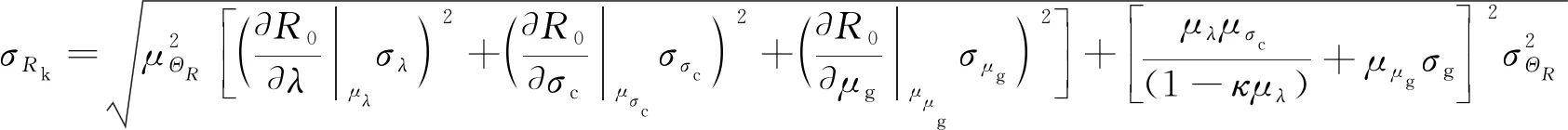
(33)
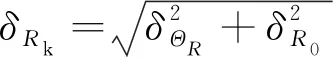
(34)
4 大数据挖掘模型及算法改进
大数据挖掘的主要目标是基于大量数据分析研究,以有效的信息手段和计算方法,获取未知且潜在的不确定信息样型和规则,提取数据内部深度的模糊随机特征及其价值,为行业决策和工程实践提供更加有效资料。
4.1 大数据HMM模型
隐马可夫模型(HMM)为一个双重的随机过程,它的状态不能直接观察得到,但能通过观察向量隐式推导获得[19]。隐马尔科夫模型的主要构成要素如下:
(1)模型的状态。
设状态集合为S={s1,s2,…,sN},时刻t时所处的状态为qt∈S。状态间可以相互转移。
(2)状态转移矩阵。
描述状态之间如何进行转移的状态矩阵A=(aij)N×N,aij为状态转移的概率。
(3)模型的观察值。
设观察值集合V={v1,v2,…,vM},当t时刻的状态转移完成的同时,模型都产生一个可观察输出yt∈V。
(4)输出的概率分布矩阵。
描述产生输出的概率分布函数矩阵B=(bij)N×M。其中,bij=bi(j)=bi(vj)=P(yt=vj|qt=si)表示t时刻状态为si时输出为vj的概率。
(5)初始状态分布。
设π={π1,π2,…,πN}为模型的初始状态分布。其中,πi=P(q1=si)。因此,完整的隐马尔科夫模型可以用λ={A,B,π}来表示所有的参数。
4.2 HMM模型算法优化
基于大数据HMM模型,采用最大期望算法(EM)改进传统的挖掘方法,整个EM算法步骤如下:
(1)E步骤:根据参数初始值或者上次迭代的模型参数θ(n)来计算极大似然估计值:
Qi(z(i)):=p(z(i)|x(i);θ)
(35)
(2)M步骤:固定Q(z),当数据的似然性最大时,计算参数期望估计:
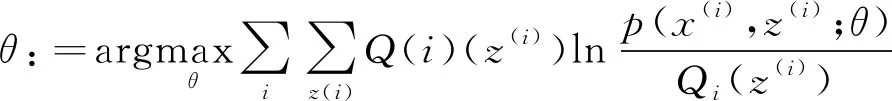
(36)
(3)重复上述EM步骤,直到‖θ(i+1)-θ(i)‖值足够小,停止迭代。
5 大数据挖掘井壁极限承载力的模糊随机模型
基于改进的大数据挖掘HMM算法,综合大数据环境下的材料性能、几何参数和计算模式的模糊随机分布,可建立大数据挖掘井壁极限承载力模糊随机模型(式(37)),算法流程如图3所示。
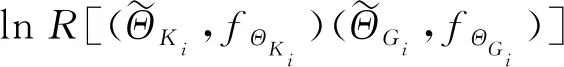
(37)

图3 大数据挖掘极限承载力模糊随机算法优化Fig.3 Fuzzy random optimization algorithm of ultimate bearing capacity with big data algorithm
利用三角型模糊隶属函数进行α截集,可得井壁极限承载力均值和标准差的模糊随机函数[20]:
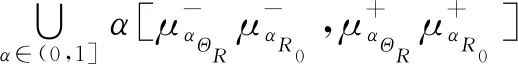
(38)
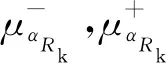
根据井壁极限承载力模糊随机分布的特点,采用三角型模糊隶属函数建立模糊随机模型[20-21],如图4所示。图中,μ(x)表示模糊隶属函数,α为约束水平,截集区间[c+(α-1)d,c+(1-α)d]随α值的增大而缩小,当α=1时就缩小为原点。

(39)

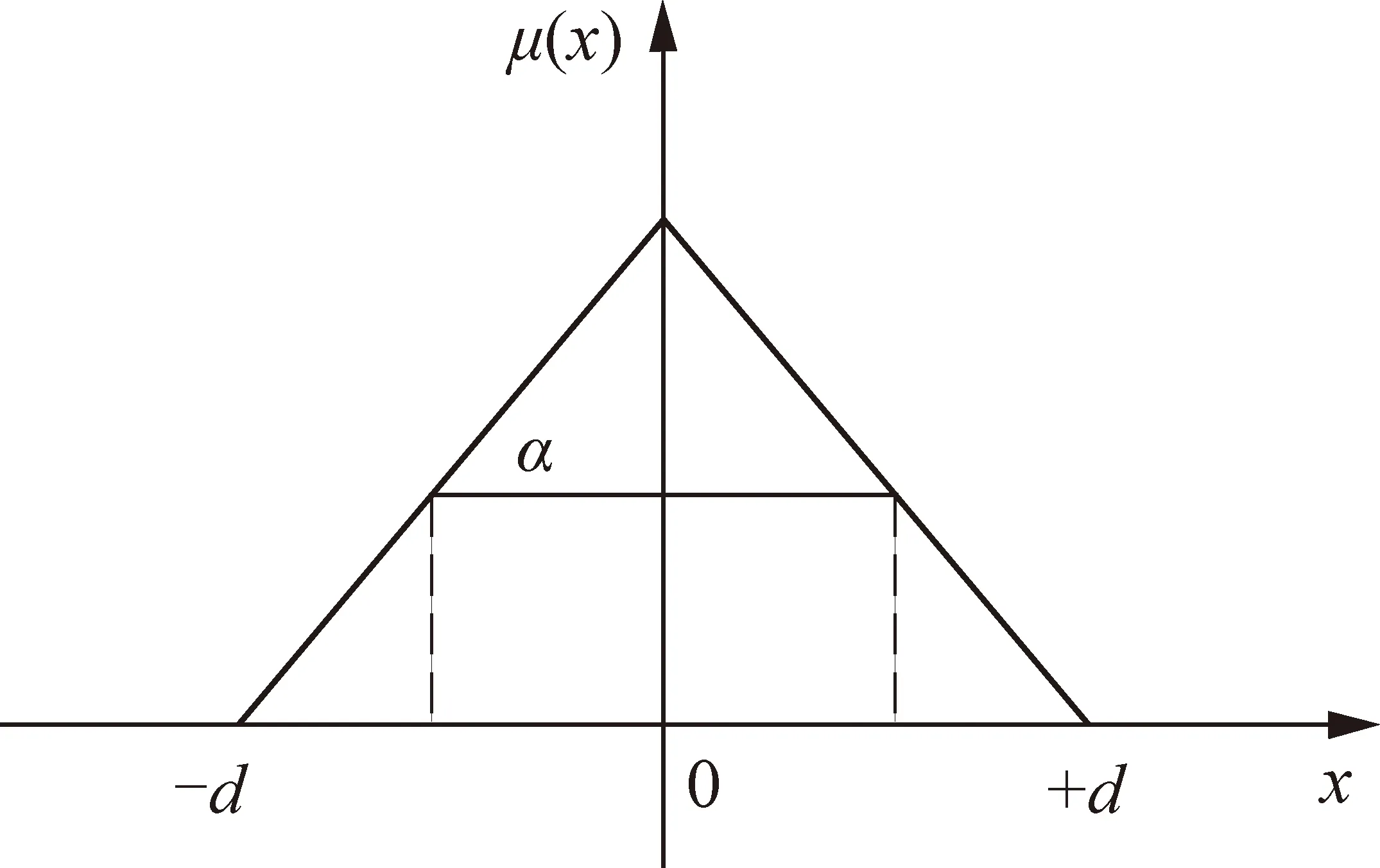
图4 三角型模糊隶属函数Fig.4 Triangular fuzzy membership function
令三角型模糊隶属函数中c取均值或标准差,d取相应值的0.1倍[22-23],模糊截集区间表示为
[μ+(α-1)0.1μ,μ+(1-α)0.1μ]或
[σ+(α-1)0.1σ,σ+(1-α)0.1σ]
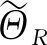
(α-1)0.08,0.850 3+(1-α)0.08]
(40)
(α-1)0.02,0.216 7+(1-α)0.02]
(41)
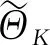
(α-1)0.1μk,μk+(1-α)0.1μk]
(42)
(α-1)0.1σk,σk+(1-α)0.1σk]
(43)

(α-1)0.1,1.033 4+(1-α)0.1]
(44)
(α-1)0.02,0.254 0+(1-α)0.02]
(45)
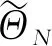
(α-1)0.1,1.040 7+(1-α)0.1]
(46)
(α-1)0.01,0.074 7+(1-α)0.01]
(47)
根据改进后的大数据挖掘算法,通过式(42)~(47)的模糊区间运算,极限承载力经验公式计算值均值的最小值和最大值可表示为
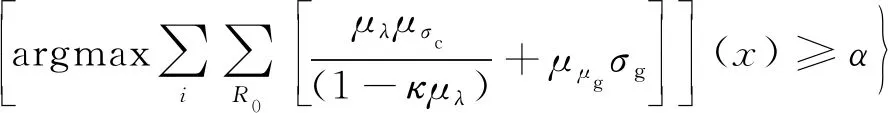
(48)
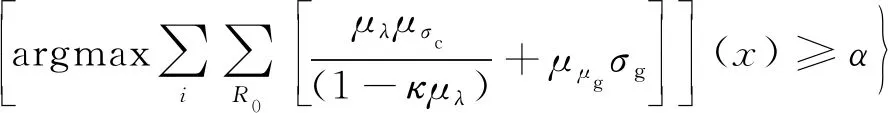
(49)
式中,inf(·)和sup(·)分别为α水平下截集区间的最小值和最大值,将极限承载力经验公式计算值的标准差展开为泰勒级数,有
同理,利用改进后的HMM算法,极限承载力经验公式计算值标准差的最小值和最大值可表示为

(51)
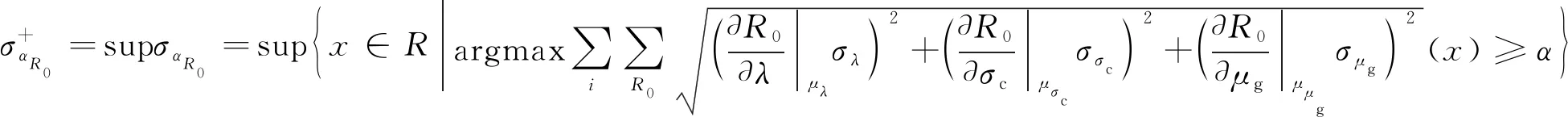
(52)
至此,将相应各式代入(37),即为大数据挖掘钢筋混凝土井壁极限承载力的模糊随机模型。
6 工程算例
两淮矿区某深厚冲积层冻结主副井筒均采用高强钢筋混凝土井壁结构,井筒穿越冲积层厚度分别为 457.78和 525.25 m。依据井壁结构特点和相似性理论,确定井壁模型的参数,试件外直径为925 mm,高为562.5 mm,通过模型试验得出井壁极限承载力的试验值,与文中大数据挖掘模糊随机模型分析值进行对比(α水平取0.75),结果见表6。
从结果分析,大数据挖掘模糊随机模型综合各种工程模糊随机因素,加上大量工程试验数据的挖掘为基础,因此得到的井壁极限承载力为一个广义区间值,虽然总体与试验值误差不大,但表征形式更加可靠合理,更具有工程实用价值。另外,由于考虑到工况的模糊随机性,使得模型分析值整体比试验值要小,如图5所示,其结果更加符合工程实际。
表6 大数据挖掘极限承载力的模糊随机值与试验值对比
Table 6 Comparison between big data fuzzy random and experimental results of shaft lining ultimate bearing capacity
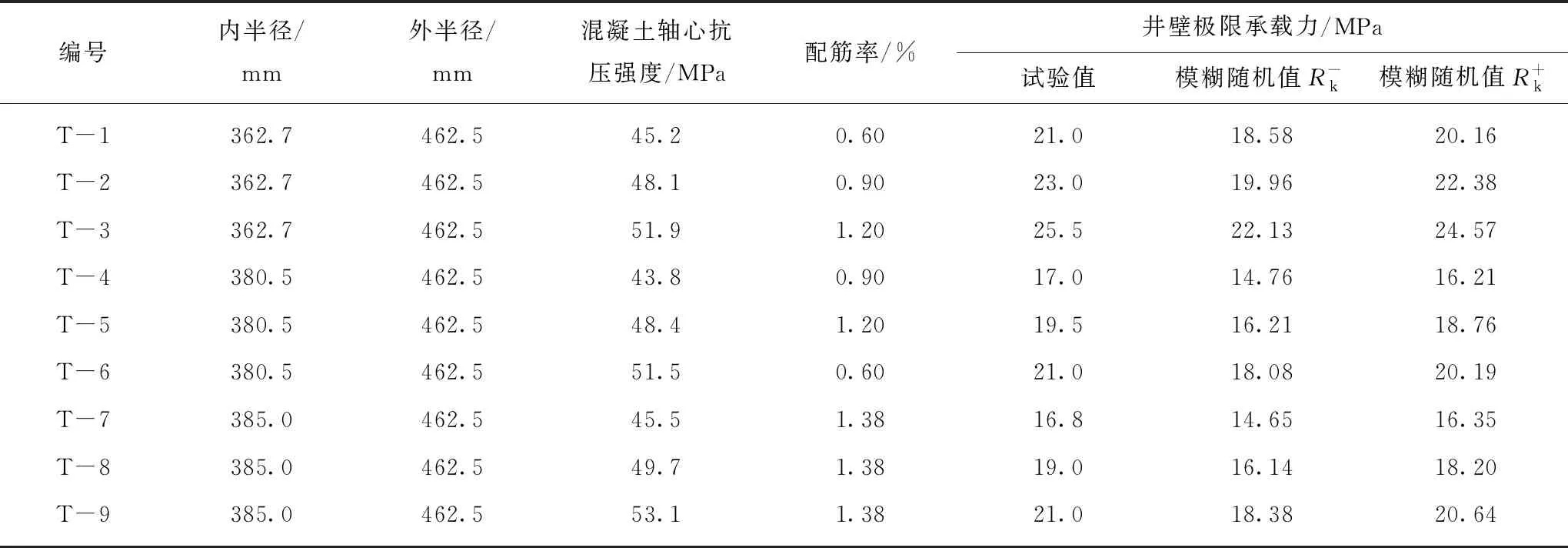
编号内半径/mm外半径/mm混凝土轴心抗压强度/MPa配筋率/%井壁极限承载力/MPa试验值模糊随机值R-k模糊随机值R+kT-1362.7462.545.20.6021.018.5820.16T-2362.7462.548.10.9023.019.9622.38T-3362.7462.551.91.2025.522.1324.57T-4380.5462.543.80.9017.014.7616.21T-5380.5462.548.41.2019.516.2118.76T-6380.5462.551.50.6021.018.0820.19T-7385.0462.545.51.3816.814.6516.35T-8385.0462.549.71.3819.016.1418.20T-9385.0462.553.11.3821.018.3820.64
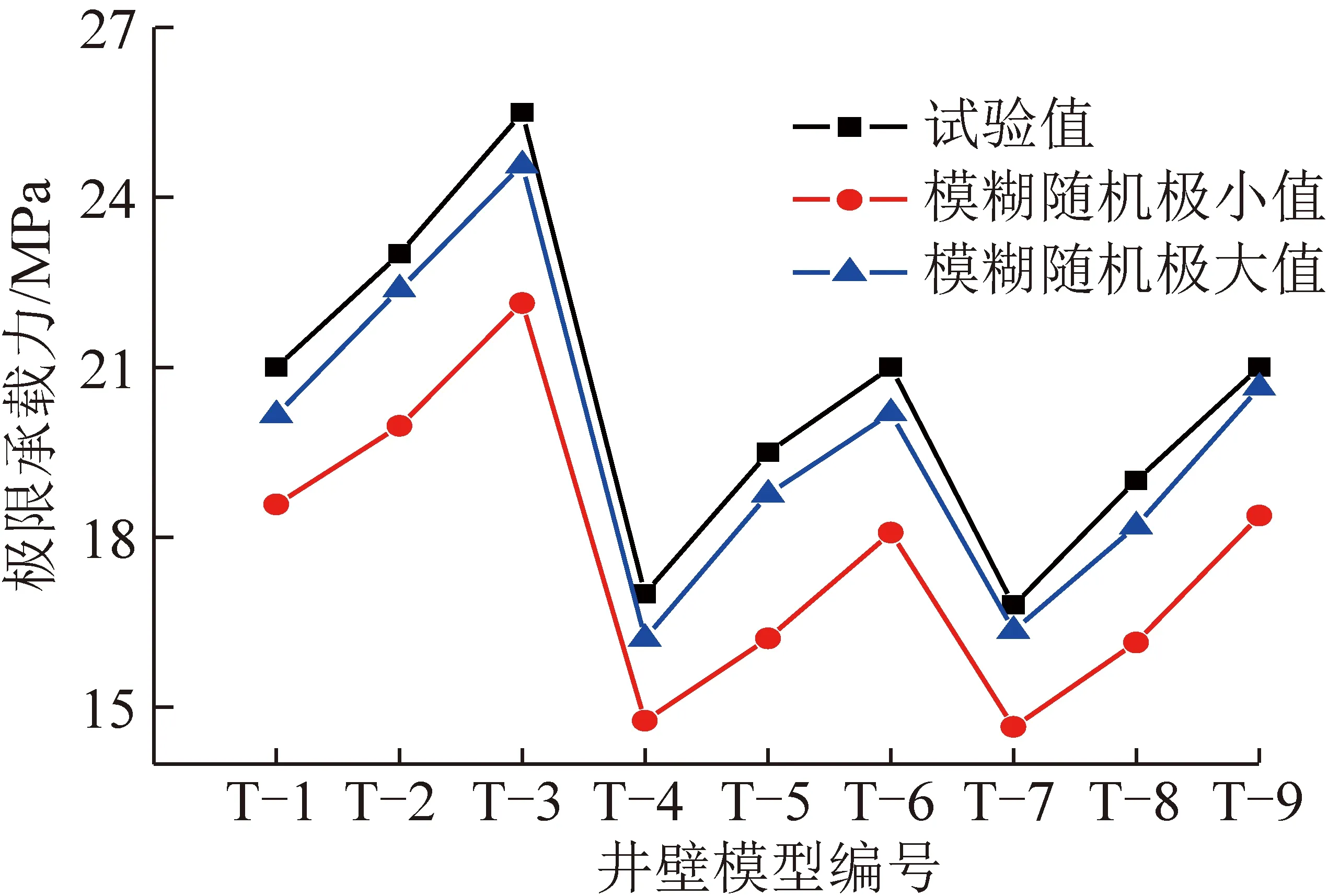
图5 极限承载力值对比Fig.5 Comparison of ultimate bearing capacity value
在配置RedHat 9.0系统的LUNIX主机上,通过Matlab 2016 A软件进行算法效率数值模拟。以上述井壁模型极限承载力试验数据为基础,分别使用传统HMM模型和EM优化后的模型进行计算模拟,算法效率对比曲线如图6所示。
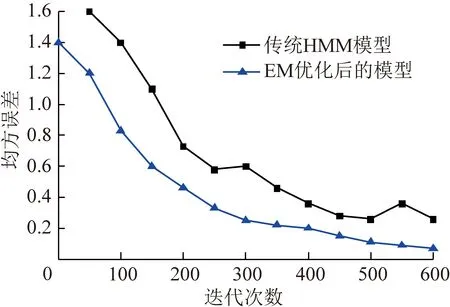
图6 算法效率对比Fig.6 Contrast of algorithm efficiency
由图16可知,随着问题规模的增加,EM优化后的算法相比传统的HMM算法误差越来越小、运算效率也越来越高,收敛速度也越来越快。
7 结 论
(1)通过大量钢筋混凝土井壁模型极限承载力试验可知,影响井壁承载力的主要因素为混凝土抗压强度、厚径比和配筋率。其中,混凝土抗压强度对井壁承载力影响最为明显,配筋率影响最弱。
(2)综合考虑井壁结构材料的不确定性、几何参数的不确定性和计算模式的不确定性,以大量井壁试验和两淮矿区的井筒工程参数作为样本数据集,分析混凝土抗压强度、厚径比和配筋率等主要参数的不确定分布情况,得到相应的模糊随机分布规律。
(3)采用最大期望算法优化原大数据HMM挖掘模型,分别经过E步骤计算极大似然估计值和M步骤计算参数期望估计,改进后模型经过两次模糊随机过程,相比原算法更能满足工程的不确定特性。
(4)基于改进的大数据挖掘HMM算法,综合大数据环境下的材料性能、几何参数和计算模式的模糊随机分布,建立大数据挖掘井壁极限承载力模糊随机模型,实例证明该模型更加可靠合理,更具有工程实用价值,可为今后深厚冲积层中钢筋混凝土井筒设计提供参考依据。
