京张高铁东花园长大明挖隧道衬砌结构变形特征研究
2020-04-23周广平
周广平
(中铁十八局集团有限公司, 天津 300222)
0 引言
基于新建京张高铁工期紧、任务重,加上东花园隧道是明挖隧道,为加快工期,防止隧道衬砌裂缝的大量发生,进行现场明挖隧道衬砌的测试研究非常有必要。
衬砌结构的应力应变监测是评价隧道施工方法可行性、设计参数合理性的重要手段,能对隧道施工过程中实际受力及其变形特性等提供准确的信息,也可为现场实际情况提供可靠的数值参考,对于保证明挖隧道建设和建成后的运营期安全性十分重要[1-3]。
目前,有不少学者针对隧道裂缝问题做了大量的研究工作。余晶[4]利用有限元分析,研究了隧道衬砌不同位置处裂缝对结构受力的影响;张芳等[5]基于荷载-结构模型,利用FDEM对衬砌在不同因素下的裂缝形成部位、外观、扩展规律等进行了研究;刘德军等[6]在统计分析大量隧道裂缝后,提出了一种早强型基体材料来对衬砌进行加固;李宇杰等[7]在隧道存在既有裂缝的情况下,通过模拟计算研究了隧道衬砌受力、损伤和承载力状态;孙克国等[8]以应力监测为基础,采用有限元软件对隧道衬砌结构在不同级别围岩下的受力状态进行模拟,以监测位移值做为标准,并对数值模拟结果的正确性进行验证。荣耀等[9]通过模型试验探讨了锈蚀钢筋混凝土偏压构件和普通钢筋混凝土偏压构件裂缝发生和发展的演变规律,对模型构件加载下的裂缝扩展宽度、扩展速度及扩展加速度进行了分析;叶飞等[10]通过对量测数据的整理分析,对衬砌结构的承载状况及安全性进行了诊断和评价;张素磊等[11]从勘察设计、施工以及运营管理3个环节对隧道衬砌裂缝成因进行了系统分析,并据此提出了隧道衬砌裂缝预防措施;张晓东等[12]针对某公路隧道完工后边墙及拱部出现各种类型裂缝的情况,在对裂缝分类统计的基础上,监测和分析典型裂缝,从地质条件、工程设计和施工技术等方面分析裂缝成因,并根据实际情况,采取了有效的防裂措施,并取得了良好的效果。
然而,以上研究都是集中在隧道衬砌裂缝出现问题而进行的现场调研、现场监测和数值分析,仅有文献[13-15]对明挖隧道的施工裂缝展开研究,但也仅仅从混凝土施工裂缝的类型入手展开分析其裂缝产生的原因,并没有对明挖隧道的施工期衬砌进行现场测试,没有基于有限元分析衬砌不同位置处的应力、应变,得出相应的规律,从而优化施工和设计方案,减少裂缝的发生,加快施工进度。
本文通过现场测试和有限元分析,对高速铁路明挖隧道的衬砌结构从支模至衬砌结构达到设计强度的整个过程进行应变与应力分析,并探讨长大明挖隧道裂缝的产生位置和机制。
1 工程概况
新建京张高铁东花园高速铁路隧道全长4 970 m,其中进口左线内轨顶面高程485.287 m,出口左线内轨顶面高程487.537 m,DK82+770~DK83+450长680 m按-25‰放坡度,DK83+450~DK85+100长1 650 m按-3‰放坡度,DK85+100~DK87+000长1 900 m按3‰放坡度,DK87+000~DK87+740长740 m按25‰放坡度,同时设计速度350 km/h,最大覆盖层厚度8.1 m。全隧采用明挖法施工,最大开挖深度21.69 m,标准段开挖宽度64.94 m。东花园隧道平面图和纵断面图如图1和图2所示。

图1 东花园隧道平面图

图2 东花园隧道纵断面图(单位: m)
2 数值计算
运用MIDAS软件,采用摩尔-库仑模型对明挖隧道(隧道宽×高=14.9 m×12.68 m,衬砌厚度为0.8 m)衬砌所受轴力、剪力和弯矩进行相关的二维平面分析,通过理论计算找到轴力、剪力、弯矩的受力最大处,并分析其随着位置变化导致结构受力的变化。同时,根据有限元结果选择典型断面的相应位置处进行现场试验。
对明挖隧道的衬砌受力进行了建模计算分析,根据隧道实际断面尺寸绘制了相应模型。整个衬砌模型模拟为梁单元受力,断面厚度为70 cm,长度截取1 m,衬砌材料参数采用C40混凝土相应参数设计。在受力方面,由于明挖隧道在未回填之前整个衬砌结构仅仅受到自身重力的影响,因此在模型计算时添加的外力仅有自重一项。在约束方面,明挖隧道未回填之前衬砌结构仅有下部仰拱受到相应土体的约束,故仅在仰拱下部施加约束。约束模拟为弹性地基约束,由于隧道开挖底部的基础岩土不能抵抗拉伸,因此应使地基弹簧执行使用受压单元的边界非线性分析。根据建模结果得到相应的轴力、剪力及弯矩云图如图3—5所示。

图3 轴力云图(单位: kN)

图4 剪力云图(单位: kN)

图5 弯矩云图(单位: kN·m)
分析模型计算结果,衬砌所受轴力均为压力,在拱顶处衬砌所受轴力最小,而在边墙下部处衬砌所受轴力最大(不考虑仰拱),即从拱顶开始,沿着衬砌两侧从上到下轴力逐渐增大,两侧轴力对称分布;并且两侧拱腰截面与拱肩截面处轴力差值并不大。
衬砌整体受剪力作用并不显著。左右两侧所受剪力并不对称,左侧底部边墙处剪力较大且为负值,沿左侧底部边墙往上剪力逐渐减小,拱腰位置附近由负值变为正值;继续向上剪力值变化不大,在拱顶位置处剪力又从正值变化为了负值,沿右侧衬砌向下,在右侧拱腰位置附近又由负值变化为正值,右侧边墙底部剪力为正值最大值。两侧拱腰截面处均为剪力发生正负变化的位置,而两侧拱肩处左侧为正、右侧为负,但值均较小。
两侧弯矩对称分布,拱顶处衬砌受正弯矩作用,沿拱顶向下在两侧拱肩靠上位置处弯矩由正值变为负值,且沿衬砌向下弯矩逐渐增大,在拱腰位置处弯矩最大;继续向下负弯矩逐渐减小,在边墙处又由负值变化为正值,在边墙最低处达到了正弯矩最大值。对比拱腰截面处弯矩与拱肩截面处弯矩,二者差异较为显著,拱肩处所受弯矩较小,而拱腰处所受弯矩很大,二者均为负弯矩。
3 监测实施方案
3.1 横纵断面布置
明挖隧道衬砌的监控量测项目及使用仪器为: 混凝土浇筑过程中产生的应变由振弦式应变计测得,压力由土压力计测得,钢筋轴力由振弦式钢筋计测得,外模台车的表面应变由振弦式表面应变计测得。
在纵向方向上选取2个位置,即2组横截面进行仪器布置,分别为距端口7.5 m左右的1/2截面处以及距端口1.5 m左右的端部截面处,如图6所示。
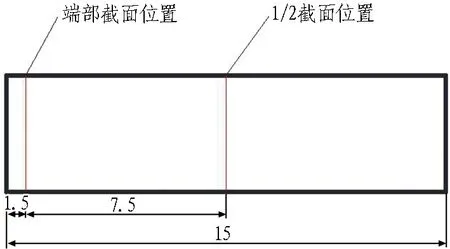
图6 试验段纵向布置位置(单位: m)
根据现场实际观测情况来看,隧道产生的裂缝均在矮拱腰位置处,同时模板台车外模变形最大的位置也位于拱腰附近,所以选定拱腰位置为一测量位置,将仪器布置在对称的两侧拱腰处。同时,选定拱肩位置处为另一测点,通过拱肩与拱腰位置处受力变形的对比分析,更加直观地体现形成裂缝位置处的受力变形,故将仪器同样布置于对称的两侧拱肩处,如图7所示。
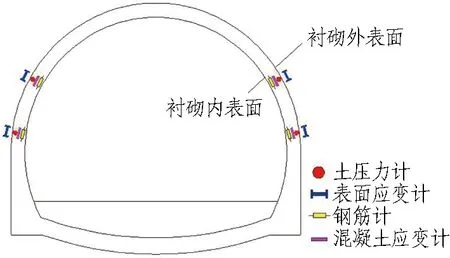
图7 横断面测点布置图
3.2 监测频率
按照图7埋设元件,在元件埋设后,根据表1的监测频率用读数仪进行监测,每一次监测次数不应少于3次,力求监测数据的可靠和稳定,取其平均值作为当次数据,并将监测数据及时记录在专用的表格中,通过相应的计算公式转化为相应内力。
表1 内力监测元件观测频率
Table 1 Observation frequency of internal force monitoring component

项目监测阶段/d监测频率所有项目11 次/2 h2~41 次/4 h5~105 次/1 d>101 次/2 d
4 监测结果分析
4.1 概述
在1#工作面安装试验元器件并进行相关监测,由于衬砌裂缝大多在衬砌混凝土浇筑完毕后3 d左右形成,故将所测数据截取为4 d内的数据进行研究分析。对每一个元器件均绘制了相关的时间-应力(应变)曲线,且对每一种元器件在相同横截面不同位置处(即同一横截面的拱肩与拱腰位置)均进行了相应的对比分析,包括混凝土应变对比分析、钢筋应力对比分析、混凝土压力值对比分析以及表面应变值对比分析。同时,将所测得的实际数据与理论计算所得数据进行相应对比,看得出的结论是否一致。由这一系列的对比,分析出产生裂缝的相关原因以及结论,并给出相关的改进方案。
4.2 1/2截面处实测分析
4.2.1 1/2截面处钢筋应力
根据实际现场观察,80%以上的衬砌裂纹均出现在1/2截面附近,故对该截面进行重点监测和分析,端部截面处的监测结果作为辅助分析。
1/2截面处钢筋应力如图8所示。6张图虽具体数值有所差异,但整体趋势基本一致。从图8中可以看出: 当浇筑混凝土刚开始时,由于混凝土聚积在模板台车的下部,所以导致初始时的钢筋是受拉的,且拉力随着下部混凝土的增多而有所增大;随着浇筑混凝土高度的逐渐升高,钢筋应力逐渐由受拉变为受压,随后一直承受压力。
对于1/2截面处的钢筋应力来说,无论是在拱肩处受力,还是在拱腰处受力,二者相差不大,拱腰处应力值略大于拱肩处应力值。在55~60 h应力发生了突变,而混凝土的凝结硬化时间也基本在此时进行,这一时间内拉应力大于混凝土强度,所以大多数裂缝均是在此时出现的。
(a) 右侧拱腰钢筋应力 (b) 左侧拱腰钢筋应力 (c) 右侧拱肩钢筋应力
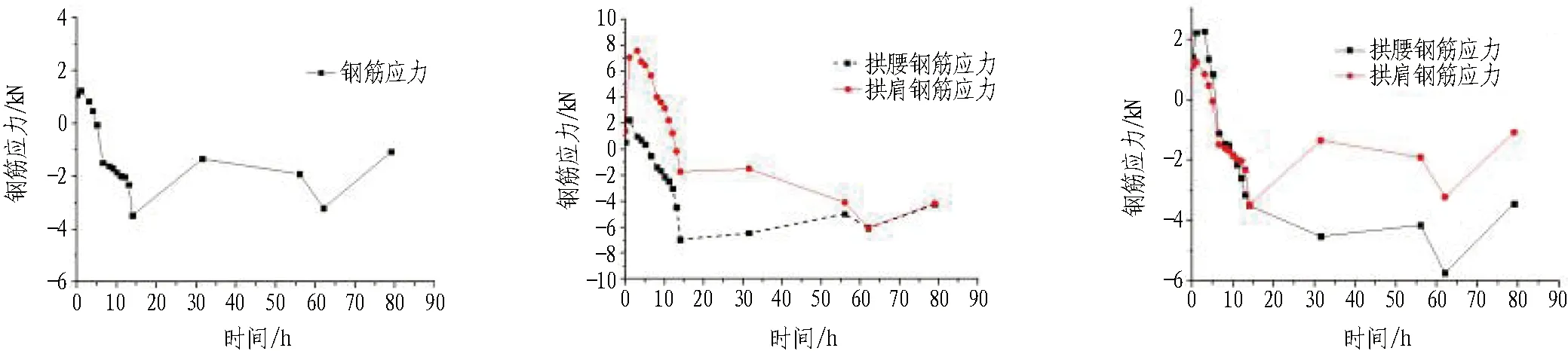
(d) 左侧拱肩钢筋应力 (e) 右侧拱腰拱肩钢筋应力 (f) 左侧拱腰拱肩钢筋应力
图8 1/2截面处钢筋应力
Fig. 8 Middle steel bar stress at one-half cross-section
4.2.2 1/2截面处混凝土应变
1/2截面处混凝土应变如图9所示。从图9中可以看出: 混凝土从一开始所受的应变即为压应变,由于在浇筑混凝土过程中会进行不断的振捣,所以混凝土应变有起伏变化的情况,但整体上随着浇筑混凝土的进行,混凝土压应变不断增大;在混凝土浇筑完毕后,可以看到压应变随着时间略微减小,这是因为当拆模后施加在衬砌上的约束减小,混凝土能够发生一定程度的自由变形,因此内部压应变也相应减小。
对比右侧拱腰与拱肩的混凝土压应变,发现拱腰处压应变的值远远大于拱肩处压应变的值。这是因为对于拱腰处的混凝土存在下方已经凝结硬化完成的矮边墙对它的约束,使其几乎不能产生自由变形,从而其内部应变会很大;而拱肩处则缺少这样的必要约束,导致拱肩处能够相对发生水平移动,使其内部应变减小。正是这样的差异使得拱腰处的应变值远大于拱肩处的应变值。由于混凝土此时的强度并未达到最终强度,一旦应变值超过此时混凝土的承受范围,就会导致拱腰附近的混凝土衬砌开裂。
4.2.3 1/2截面处混凝土压力
1/2截面处混凝土压力如图10所示。从图10中可以看出: 混凝土压力随着混凝土的浇筑过程逐渐增大,在浇筑完成后,混凝土压力增长较为迅速,这说明混凝土强度在不断提高;在55~60 h混凝土压力有所降低,此时约为混凝土凝结硬化的时间,也是拉应力大于混凝土强度的时间,一旦内部应力应变过大,极易使混凝土产生裂缝。
由于在未回填阶段混凝土仅受自重的影响,所以拱腰处混凝土压力大于拱肩处混凝土压力。因为拱腰处的混凝土承受的压力更大,而二者的强度基本一致,所以相比于拱肩,拱腰处更容易产生裂缝。
4.2.4 1/2截面处外模台车表面应变
1/2截面处外模台车表面应变如图11所示。从图11中可以看出: 在浇筑初期,外模台车的表面应变迅速增大,而后逐渐趋于平稳,在拆模之前没有了大的波动,所以这就要求在浇筑混凝土初期一定要控制浇筑速度,保证施工安全;外模台车所受应变均为拉应变,正是由于衬砌混凝土的不断浇筑导致外模台车发生轻微的膨胀变形,从而产生了拉应变。
对比左侧拱腰与拱肩处的外模台车表面应变,可以看出二者并不存在数值上的显著差异,拱腰处值略大于拱肩处。
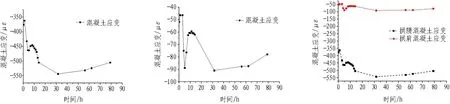
(a) 右侧1/2截面处拱腰混凝土应变(b) 右侧1/2截面处拱肩混凝土应变 (c) 右侧1/2截面处拱腰拱肩混凝土应变
图9 1/2截面处混凝土应变
Fig. 9 Concrete strain at one-half cross-section
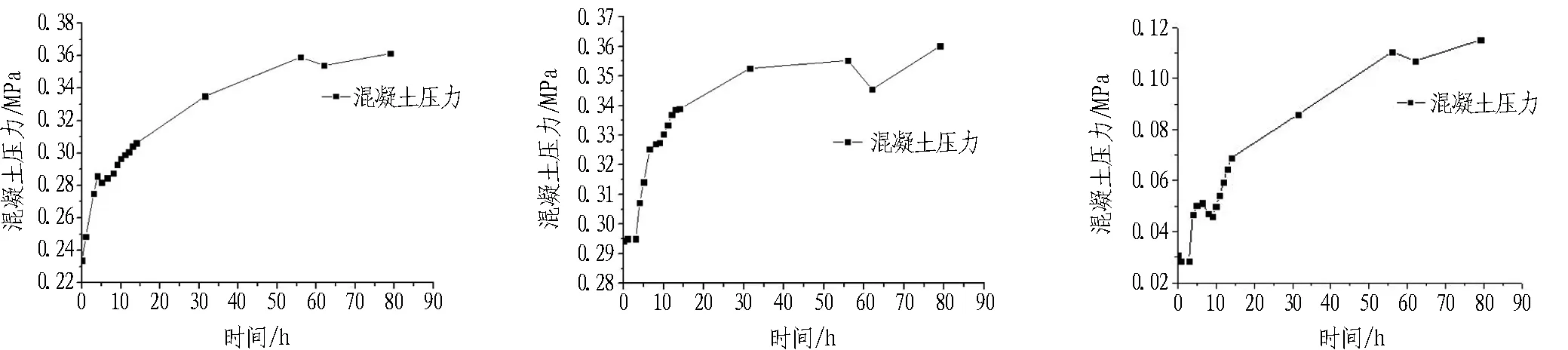
(a) 右侧1/2截面处拱腰混凝土压力 (b) 左侧1/2截面处拱腰混凝土压力 (c) 右侧1/2截面处拱肩混凝土压力

(d) 左侧1/2截面处拱肩混凝土压力 (e) 右侧1/2截面处拱腰拱肩混凝土压力 (f) 左侧1/2截面处拱腰拱肩混凝土压力
图10 1/2截面处混凝土压力
Fig. 10 Concrete pressure at one-half cross-section

(a) 左侧1/2截面处拱腰外模台车表面应变 (b) 左侧1/2截面处拱肩外模台车表面应变 (c)左侧1/2截面处拱腰拱肩外模台车表面应变
图11 1/2截面处外模台车表面应变
Fig. 11 Surface strain of outer model trolley at one-half cross-section
4.3 端部截面处应力应变实测结果
4.3.1 端部截面处钢筋应力
图12示出端部截面处钢筋应力图。6张图虽具体数值有所差异,但整体趋势基本一致。从图12中可以看出: 当刚开始浇筑混凝土时,由于混凝土聚积在模板台车的下部,所以导致初始时的钢筋是受拉的,且拉力随着下部混凝土的增多而有所增大;随着浇筑混凝土高度的逐渐升高,钢筋应力逐渐由受拉变为受压,随后一直承受压力。
对于端部截面处的钢筋应力来说,无论是在拱肩处受力还是在拱腰处受力,二者相差不大,未出现明显的应力差距,拱肩处应力值略大于拱腰处应力值。在55~60 h应力发生了突变,而混凝土的凝结硬化时间也基本在此时进行,同时也是拉应力大于混凝土强度的时间,这一时间的变化尤为明显,所以大多数裂缝均是在此时出现的。
4.3.2 端部截面处混凝土应变
图13示出端部截面处混凝土应变图。在监测过程中,左侧端部截面拱腰处混凝土应变计在监测14 h后发生了破坏,因此未能测得14 h后的相应数值。从图13中可以看出: 无论是左侧还是右侧,在浇筑前期拱腰处混凝土均为拉应变,虽然混凝土不能承受拉力,但此时为混凝土浇筑初期,强度尚未成型,即使存在拉应变,对后期混凝土强度也不会产生太大的影响;随着浇筑过程的不断进行,拱腰处的拉应变不断减小,最后趋于0。

(a) 右侧端部拱腰钢筋应力 (b) 左侧端部拱腰钢筋应力 (c) 右侧端部拱肩钢筋应力

(d) 左侧端部拱肩钢筋应力 (e) 右侧端部拱腰拱肩钢筋应力 (f) 左侧端部拱腰拱肩钢筋应力
图12 端部截面处钢筋应力
Fig. 12 Reinforcement axial force at end cross-section
4.3.3 端部截面处混凝土压力
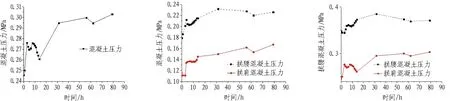
图14示出端部截面处混凝土压力图。从图14中可以看出: 混凝土压力随着混凝土的浇筑过程整体上逐渐增大;在浇筑前期,混凝土压力迅速增长,而后较为平缓;在浇筑完成后,混凝土压力增长较为迅速,这说明混凝土强度在不断提高;在55~60 h混凝土压力有所降低,也是拉应力大于混凝土强度的时间,一旦内部应力应变过大,极易使混凝土产生裂缝。
由于在未回填阶段混凝土仅受自重的影响,所以拱腰处混凝土压力大于拱肩处混凝土压力。因为拱腰处的混凝土承受的压力更大,而二者的强度基本一致,所以相比于拱肩,拱腰处更容易产生裂缝,且55~60 h是裂缝形成的高发期。
4.3.4 端部截面处外模台车表面应变
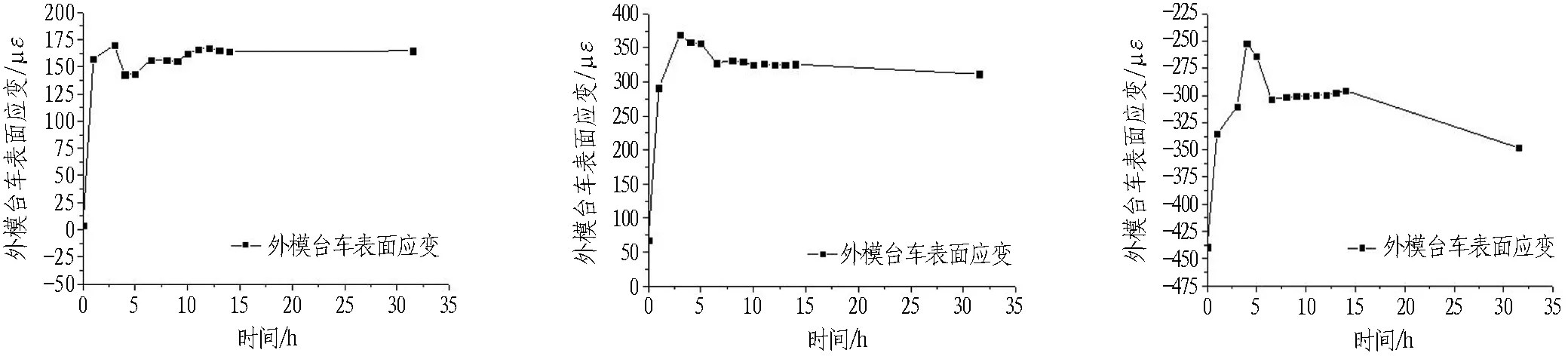
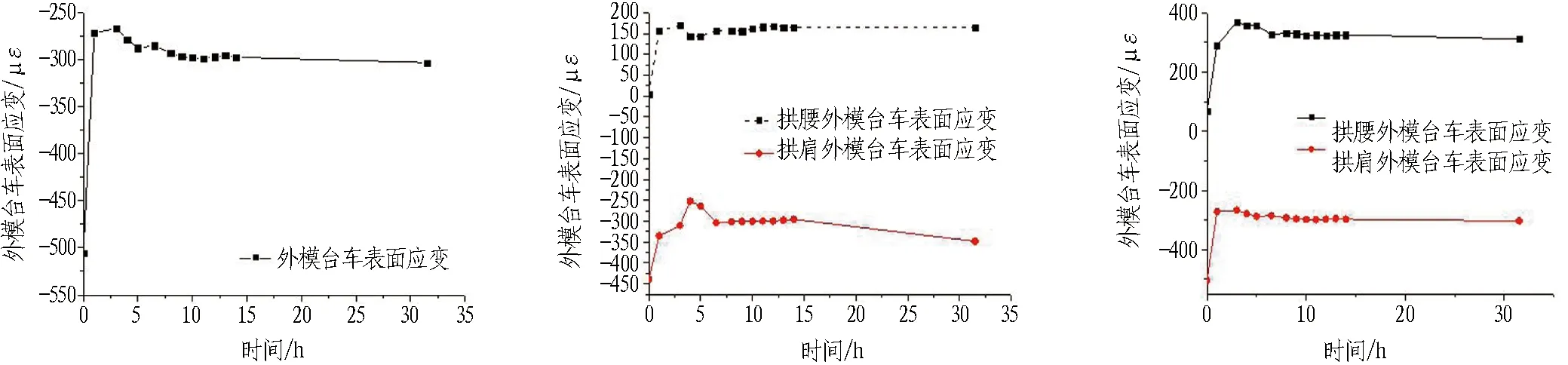
图15示出端部截面处外模台车表面应变图。从图15中可以看出: 在浇筑初期,外模台车的表面应变迅速增大,而后逐渐趋于平稳,在拆模之前没有了大的波动,这就要求在浇筑混凝土的初期一定要控制浇筑速度,保证施工安全;拱腰处外模台车所产生的应变均为拉应变,而拱肩处外模台车所产生的应变则为压应变。正是由于衬砌混凝土的不断浇筑导致外模台车发生轻微变形,而拱腰处的混凝土压力值远大于拱肩处的混凝土压力值,这就使得拱腰处的变形更大,所以产生了拉应变。
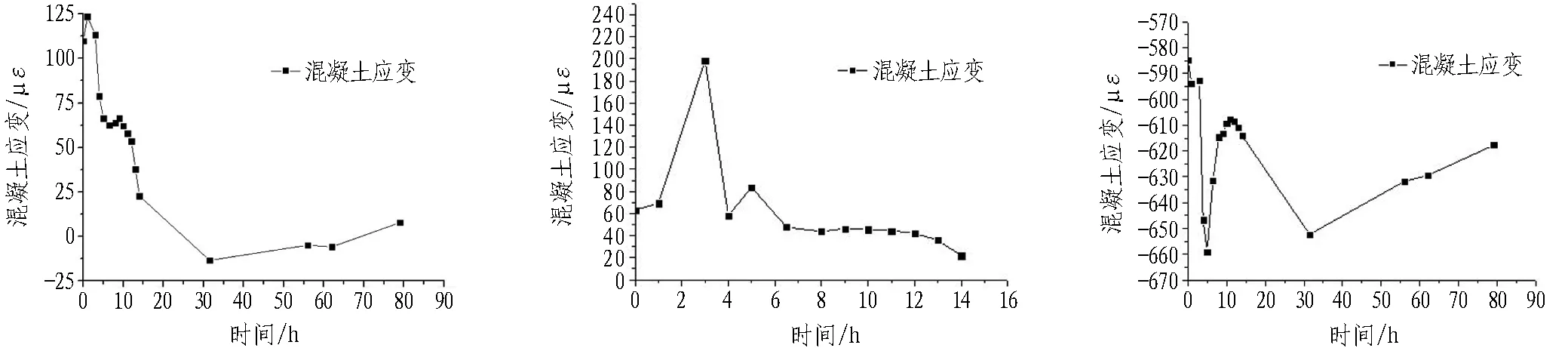
(a) 右侧端部拱腰混凝土应变 (b) 左侧端部拱腰混凝土应变 (c) 右侧端部拱肩混凝土应变

(d) 左侧端部拱肩混凝土应变 (e) 右侧端部拱腰拱肩混凝土应变 (f) 左侧端部拱腰拱肩混凝土应变
图13 端部截面处混凝土应变
Fig. 13 Concrete strain at end cross-section
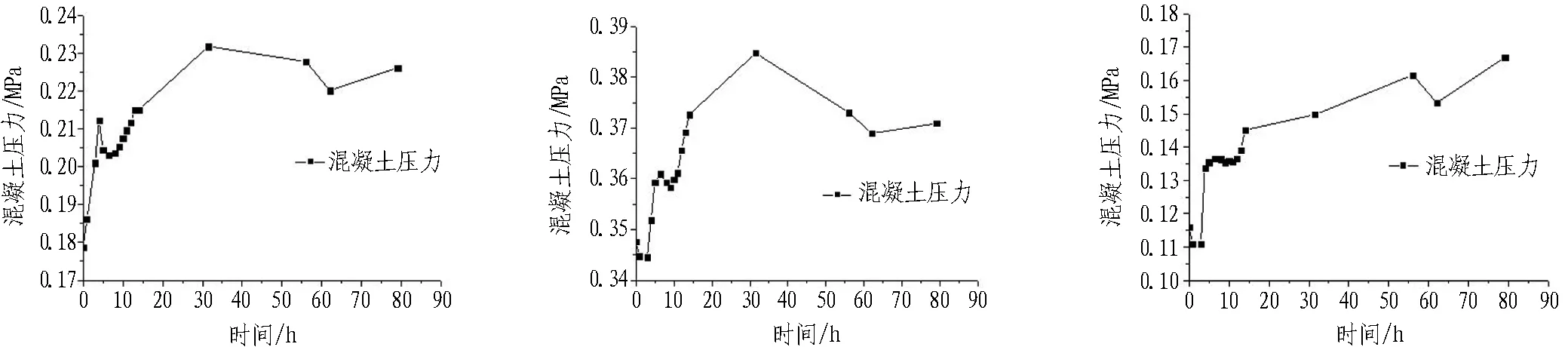
(a) 右侧端部拱腰混凝土压力 (b) 左侧端部拱腰混凝土压力 (c) 右侧端部拱肩混凝土压力
(d) 左侧端部拱肩混凝土压力 (e) 右侧端部拱腰拱肩混凝土压力 (f) 左侧端部拱腰拱肩混凝土压力
图14 端部截面处混凝土压力
Fig. 14 Concrete pressure at end cross-section
(a) 右侧端部拱腰外模台车表面应变 (b) 左侧端部拱腰外模台车表面应变 (c)右侧端部拱肩外模台车表面应变
(d) 左侧端部拱肩外模台车表面应变 (e) 右侧端部拱腰拱肩外模台车表面应变 (f) 左侧端部拱腰拱肩外模台车表面应变
图15 端部截面处外模台车表面应变
Fig. 15 Surface strain of outer model trolley at end cross-section
4.4 1/2截面与端部截面数值对比
4.4.1 钢筋应力图对比
图16示出拱腰及拱肩端部截面与1/2截面钢筋应力对比图。从图16中可以看出,环向钢筋应力无论是1/2截面还是端部截面数值相差不大,趋势也基本一致,说明在隧道环向方向上受力并不是使隧道产生裂缝的决定性因素,从现场裂缝的方向均为环向裂缝也证明了这一点。
4.4.2 混凝土应变图对比
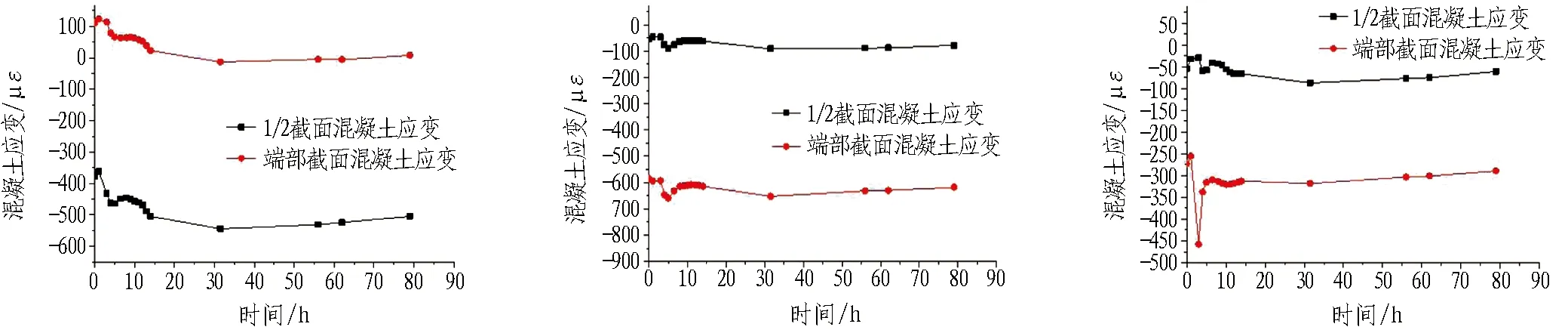
图17示出拱腰及拱肩端部截面与1/2截面混凝土应变对比图。从图17中可以看出,拱腰处1/2截面混凝土所受的压应变远大于端部截面压应变,而拱肩处则是端部截面压应变远大于1/2截面压应变。

(a) 右侧1/2截面与端部截面拱腰钢筋应力图 (b) 左侧1/2截面与端部截面拱腰钢筋应力图

(c) 左侧1/2截面与端部截面拱肩钢筋应力图 (d) 左侧1/2截面与端部截面拱肩钢筋应力图
图16 1/2截面与端部截面钢筋应力图对比
Fig. 16 Comparison of axial force between one-half cross-section and end cross-section
(a) 右侧1/2截面与端部截面拱腰混凝土应变 (b) 右侧1/2截面与端部截面拱肩混凝土应变 (c) 左侧1/2截面与端部截面拱肩混凝土应变
图17 1/2截面与端部截面混凝土应变图对比
Fig. 17 Comparison of concrete strain between one-half cross-section and end cross-section
4.4.3 混凝土压力图对比
图18示出拱腰及拱肩端部截面与1/2截面混凝土压力对比图。从图18中可以看出,对于拱腰位置,两侧的情况出现了一些差异,右侧1/2截面混凝土压力较大,而左侧端部截面混凝土压力较大。对于拱肩位置,左右两侧均是端部混凝土压力较大,而1/2截面混凝土压力较小。
4.4.4 外模台车表面应变图对比
图19示出左侧拱腰及拱肩端部截面与1/2截面外模台车表面应变对比图。从图19中可以看出: 无论拱肩还是拱腰处,1/2截面的表面应变均大于端部截面,只是拱腰处二者均为拉应变,而拱肩处端部为压应变,故拱肩处外模台车表面应变绝对值相差不大。

(a) 右侧1/2截面与端部截面拱腰混凝土压力 (b) 左侧1/2截面与端部截面拱腰混凝土压力
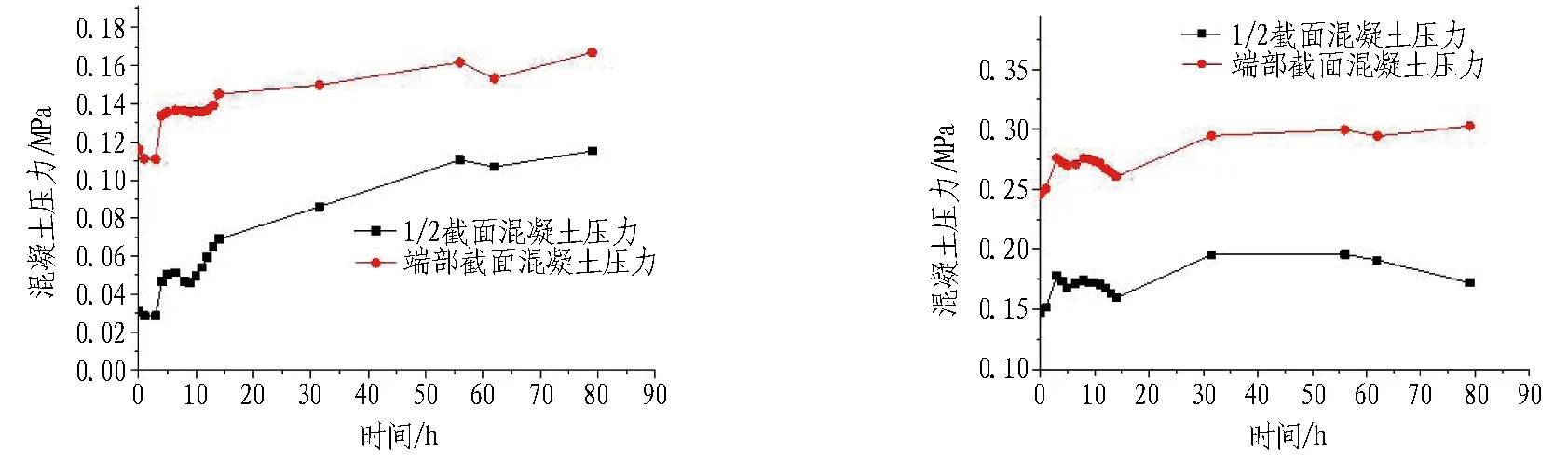
(c) 右侧1/2截面与端部截面拱肩混凝土压力 (d) 左侧1/2截面与端部截面拱肩混凝土压力
图18 1/2截面与端部截面混凝土压力图对比
Fig. 18 Comparison of concrete pressure between one-half cross-section and end cross-section
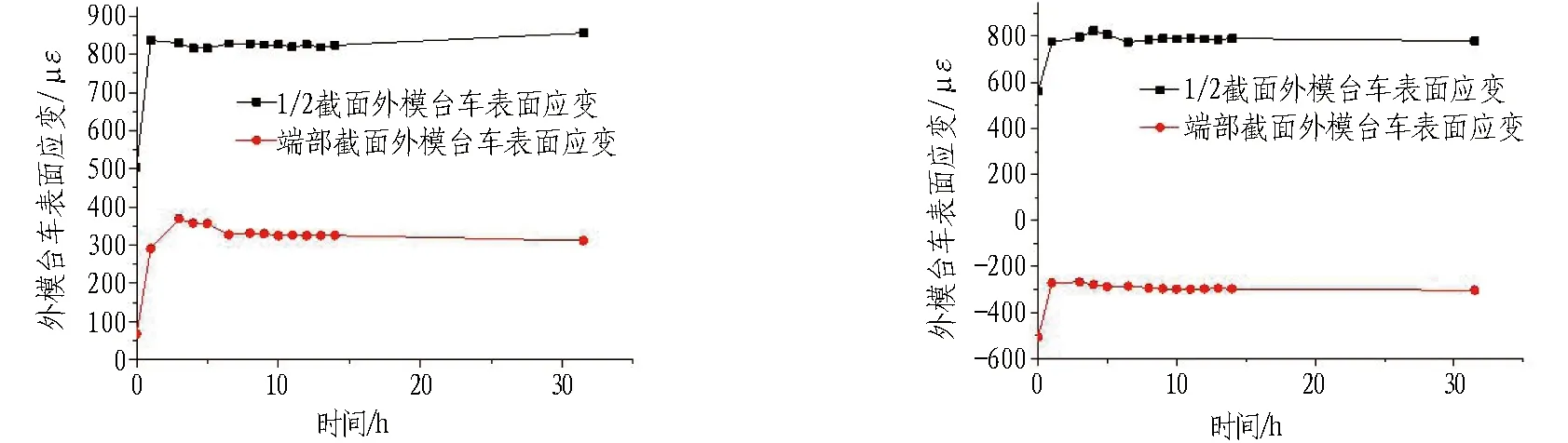
(a) 左侧1/2截面与端部截面拱腰外模台车表面应变 (b) 左侧1/2截面与端部截面拱肩外模台车表面应变
图19 1/2截面与端部截面外模台车表面应变图对比
Fig. 19 Comparison of surface strain of outer model trolley between one-half cross-section and end cross-section
5 结论与建议
1)隧道衬砌裂纹均出现在1/2截面附近的矮边墙上部及起拱线以下位置,且均为环向裂纹,这说明混凝土内部的应力应变沿隧道纵向发生变化。
2)通过数值计算与实测数据对比分析,无论是钢筋应力、混凝土应变,还是混凝土压力值,拱腰处均大于拱肩处,当两者混凝土强度大致相同的情况下,拱腰处更易形成裂缝。
3)监测期间混凝土强度尚未完成,在强度升高的过程中又伴随着大量水化热的生成,混凝土衬砌在水化热峰值临界点后逐渐降温,此过程会引起混凝土的收缩变形。对于矮边墙上部及起拱线以下的混凝土来说,其降温产生的收缩变形会受到矮边墙钢筋剪力的约束,使其不能发生水平位移,内部的应力应变有所增加,当混凝土本身的强度不足以抵抗内部的应力应变时,就会导致混凝土开裂。但上部几乎不受环向钢筋剪力影响,可自由发生水平位移,内部应变减小,故不会形成裂纹。这是隧道衬砌边墙以上至起拱线附近发生裂纹而上部没有发生裂纹的主要原因。
4)建议在矮边墙至起拱线之间增设纵向钢筋,以此来抵抗混凝土内部的应力应变,从而使衬砌裂纹不再形成,提高衬砌结构的强度和安全性。
5)根据计算结果以及现场衬砌裂纹出现的位置,建议在外模拆除后及时回填混凝土至起拱线位置,增加外侧约束,终凝后再拆除内模,可较好控制结构受力变形,加快施工进度。
