错解不是无情物 化作春泥更护花——一道“任意”与“存在”混搭问题的解法辩析

梁宝同

(安徽省颍上第一中学，236200)

在最近笔者所在学校参与的一次高三联考中,出现了如下一道关于函数中双变量的任意与存在混搭的等式问题.

题目已知函数

f(x)=alnx+x2+x-2(a∈R).

(1)若f(x)在[1,+∞)单调增,求实数a的取值范围;

(2)当a=2时,对于任意的λ∈[1,2],存在正实数x1、x2,使得f(x1)+f(x2)=λ(x1+x2),求x1+x2的最小值.

一、解法展示

解法1 (参考答案)(1)略.

(2)当a=2时,f(x)=2lnx+x2+x-2,由f(x1)+f(x2)=λ(x1+x2),整理得(x1+x2)2-(λ-1)(x1+x2)-4=2x1x2-2ln (x1x2).

由此可得(x1+x2)2-(λ-1)(x1+x2)-4≥2,即(x1+x2)2-(λ-1)(x1+x2)-6≥0对任意λ∈[1,2]恒成立.

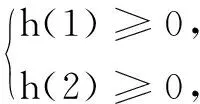
解得x1+x2≥3,所以x1+x2的最小值为3.

有学生给出如下解答.

解法2(1)略.

(2)当a=2时,f(x)=2lnx+x2+x-2.由f(x1)+f(x2)=λ(x1+x2)，整理可得-λ(x1+x2)+(x1+x2)2+(x1+x2)-2x1x2+2ln (x1x2)-4=0.

对任意λ∈[1,2],存在正实数x1、x2,使得f(x1)+f(x2)=λ(x1+x2).设g(λ)=-λ(x1+x2)+(x1+x2)2+(x1+x2)-2x1x2+2ln (x1x2)-4，则对任意λ∈[1,2],g(λ)=0有解.

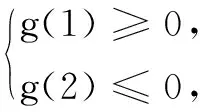
(x1+x2)2-2x1x2+2ln(x1x2)-4≥0,

①

(x1+x2)2-(x1+x2)-2x1x2+2ln(x1x2)-4≤0.

②

设x1x2=t>0,F(t)=2t-2lnt,同解法1可知,F(t)的最小值为F(1)=2.

二、正误辩析

两种解法看似都正确,但答案却不一样.其中参考答案提供的是解法1，看似无懈可击,实则偷换概念：题目叙述的是对任意的λ∈[1,2],存在正实数x1、x2,使得f(x1)+f(x2)=λ(x1+x2),而解法1正好颠倒了,变成了先存在正实数x1、x2,再对任意的λ∈[1,2],都有f(x1)+f(x2)=λ(x1+x2)成立.显然这样做题目意思就变了,但是当笔者在分析题目时,发现学生并不理解,相反大多数同学都认为解法1是正确的.当然,对于“任意”和“存在”出现顺序的辨析,本来就是个难点(不少老师也没有注意到位置的调换对逻辑关系的影响),这里笔者通过对周期函数定义的辨析,让学生悟出它们的区别.具体教学片段如下:

师:周期函数的定义:一般地,对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D,都有f(x+T)=f(x),那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.

师:如果改为如下描述:一般地,对于函数y=f(x),x∈D,如果对任意的x∈D,存在一个非零常数T,使得f(x+T)=f(x),那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.请同学们仔细体会两者的区别.

生1:定义中先有非零常数T,再对任意的x∈D,都有f(x+T)=f(x),这里的非零常数T是确定的,不变的；然而，调换“任意”与“存在”的顺序后,在变更描述中，非零常数T是不确定的、可变的.因此，两种定义方式含义不一样.

生2:我举个例子,比如y=sin|x|,显然不是周期函数,但是对于任意的实数x,都可以找到非零常数T,使得f(x+T)=f(x),所以在函数周期的定义中，不能调换“任意”与“存在”的位置.

师:很好!两位同学的思考非常正确.由此可见，“任意”与“存在”的逻辑顺序对理解题意的重要性可见一斑.那么，同学们,现在再来看看本次考试的试题,对于解法1和解法2哪个正确呢?

生:(齐声说)解法2是正确的.

通过对错解的辨析,不仅让同学们认清了错误的原因,也进一步使学生认识到数学语言叙述的严谨性.有道是错解不是无情物,化作春泥更护花.虽然上述错解看似合理,但隐藏了典型的逻辑错误.由此展开教学,更能激发学生的学习兴趣,培养学生勇于探索的精神,对于学生思维能力的培养和核心素养的提升,有着举足轻重的作用.通过与学生的交流和反思达到了教学相长、师生共贏之佳境!