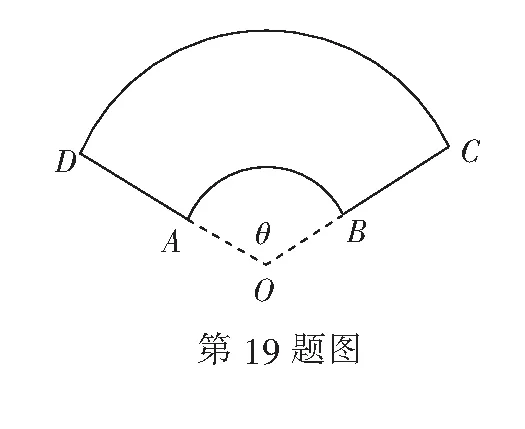
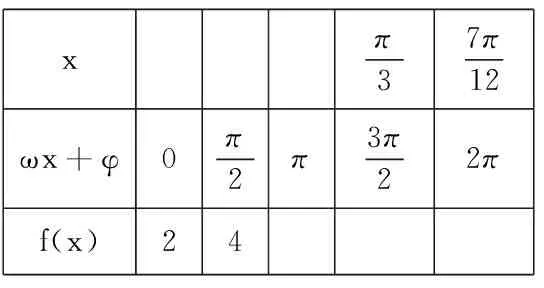
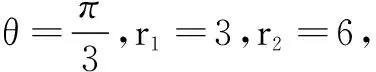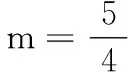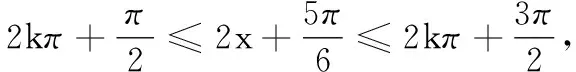高一数学测试

一、填空题(本大题共有12小题,每小题4分,共计48分)

1.已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=( )

(A){1} (B){1,2}

(C){0,1,2,3} (D){-1,0,1,2,3}

2.下列命题中正确的是( )

(A)若两个向量相等,则它们的起点和终点分别重合

(B)若a∥b,b∥c,则a∥c

(C)模相等的两个平行向量是相等向量

(D)两个相等向量的模相等

3.若角α的终边经过点P(-1,2),则cosα等于( )

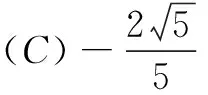
4.已知幂函数-2 2=21的值为( )

(A)y=2x(B)x> 1

(C)2 (D)16

(A)a

(C)b

(A)1个 (B)2个 (C)3个 (D)4个

8.函数y=e|ln x|-|x-1|的图象大致是( )

(A){x|x<-2或x>2}

(B){x|x<-2或0

(C){x|-22}

(D){x|-2

(A)[-1,0) (B)[-2,0)

(C)[-3,0) (D)[-4,0)

二、填空题(本大题共有4小题,每小题5分,共20分)

14.方程2x+x=4的解为x0,x0∈(k-1,k)(k∈Z),则k=______.

三、解答题(本大题共有6小题,共82分.解答时应写出必要的文字说明、证明过程或演算步骤)

(1)求M∪N;

(2)记集合P=R(M∩N),Q={x|ax-1=0},若P∩Q=∅,求a的取值范围.

19.(本小题满分12分)某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过AD、BC的两条线段围成.设圆弧AB和圆弧CD所在圆的半径分别为r1、r2米,圆心角为θ(弧度).

(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/m,弧线部分的装饰费用为90元/m,预算费用总计1 200元,问线段AD的长度为多少时,花坛的面积最大?

20.(本小题满分14分)已知函数f(x)=2x-k·2-x在定义域内具有奇偶性.

(1)求k的值;

(2)已知g(x)=4x+4-x-2mf(x)在[1,+∞)上的最小值为-2,求m的值.

(说明:如果要用到函数的单调性,可直接交代单调性,不必证明)

21.(本小题满分16分)已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0),部分自变量、函数值如下表.

xπ37π12ωx+φ0π2π3π22πf(x)24

(1)求函数f(x)的解析式、单调减区间和对称中心坐标;

22.(本小题满分14分)对于定义域为D的函数y=f(x),如果存在区间[m,n]⊆D,同时满足:①f(x)在[m,n]内是单调增函数;② 当定义域是[m,n]时,f(x)的值域是[2m,2n],则称[m,n]是该函数的“翻倍区间”.

(1)证明:[1,2]是函数f(x)=2x的一个“翻倍区间”；

(2)判断函数g(x)=x3是否存在“翻倍区间”？若存在，求出其所有“翻倍区间”;若不存在,请说明理由；

参考文献

一、选择题

1.C；2.D;3.A;4.D;5.B;6.C;

7.B;8.D;9.A;10.B;11.A;12.C.

二、填空题

三、解答题

由2x> 2=21及函数y=2x为R上的增函数，可知x> 1,即集合N=(1,+∞).

故M∪N=(-2,+∞).

(2)由(1)可得交集M∩N=(1, 2],则集合P=(-∞, 1]∪(2,+∞).

18.(1)由条件易得tanα=2.

19.(1)设花坛的面积为S平方米，则

(2) 易知圆弧AB的长为r1θm,圆弧CD的长为r2θm,线段AD的长为(r2-r1)m.

由题意知60·2(r2-r1)+90(r1θ+r2θ)=1 200，即

4(r2-r1)+3(r2θ+r1θ)=40 ，

(*)

当x=5，即r2-r1=5时,花坛的面积最大.

答:当线段AD的长为5 m时,花坛的面积最大.

20.(1)若f(x)为奇函数,则有f(-x)=-f(x),即2-x-k·2x=-2x+k·2-x恒成立,即(2x+2-x(1-k)=0恒成立,可得k=1.

若f(x)为偶函数,则f(-x)=f(x),同理可知(2x-2-x)(1+k)=0恒成立,所以k=-1.

综上，所求k=±1.

所以，当k=1时,m=2.

22.(1)由f(x)=2x在[1, 2]上单调增，可知f(x)的值域为[2, 4].故[1, 2]是函数f(x)=2x的一个“翻倍区间”.

(2)假设g(x)存在一个“翻倍区间”[m,n],由函数g(x)是R上的单调增函数,有