构造三角形数阵 妙解一类数列问题

吴家华

(四川省遂宁中学校，629000)

本文从一道引例的分析出发,把一个数列的各项依次“竖起”排列成一个“三角形数阵”,并从数阵中发现规律,从而找出解决问题的方法,而且这种方法在处理一类数列问题中具有普遍性和可操作性.

引例在数列{an}中,若a1=1,a2=2+3,a3=4+5+6,a4=7+8+9+10,…,则a10=( ).

(A) 610 (B) 510

(C) 505 (D) 750

分析由于此题求的是第10项,许多学生在解此题时,根据数列的构成规律,逐一写出各项,直到第10项而求解.但我们若将结论改为求a100,则按此方法就不容易求解了.现在我们将数列{an}中的各项依次“竖起”排成下表:

1

2 + 3

4 + 5 + 6

7 + 8 + 9 + 10

… … … … … … …

b10+(b10+1)+(b10+2)+…+(b10+9)

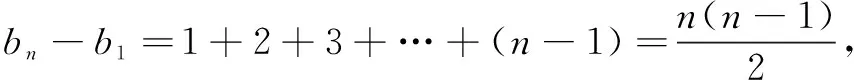
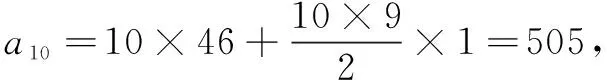
像引例这样,将已知数列{an}中的项依次“竖起”排列起来,得到一个“三角形数阵”,并从这个数阵中去发现规律,能使问题迅速得到解决. 笔者在多年的教学和解题实践中发现,借助于这种“三角形数阵”,很容易解决与引例同类的一类数列问题.请看下面几个例子.

例1将奇数数列如下分组:1,(3,5),(7,9,11),(13,15,17,19),…,使得第n组中含有n个数,那么第n组中n个奇数的和为______.

解将各组数依次“竖起”排成如下“三角形数阵”,并记第n组中的第一个数为an，

1

3 5

7 9 11

13 15 17 19

… ……………

anan+2an+4 …an+2(n-1)

则数列{an}:a1=1,a2=3,a3=7,a4=13, …,从而有a2-a1=2,a3-a2=4,a4-a3=6, …,由此可归纳出:an-an-1=2(n-1).将以上n-1个等式累加，得an-a1=2+4+6+…+2(n-1)=n(n-1)，故an=1+n(n-1)=n2-n+1.

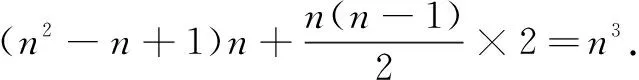
例2给定数列1,2+3+4,5+6+7+8+9,10+11+12+13+14+15+16,…,则这个数列的一个通项公式是( )

(A)an=2n2+3n-1

(B)an=n2+5n-5

(C)an=2n3-3n2+3n-1

(D)an=2n3-n2+n-2

解将数列前n项依次“竖起”排成如下“三角形数阵”,并记第n项的第一个数为bn，

1

2+3+4

5+6+7+8+9

10+11+12+13+14+15+16

… ……………

bn+(bn+1)+(bn+2)+…+[bn+2(n-1)]

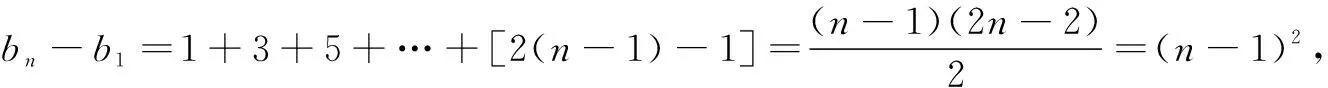
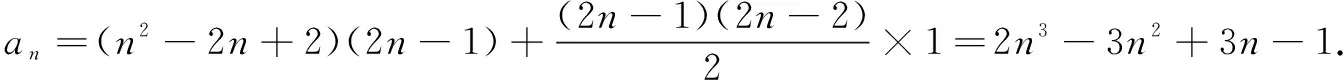
故应选C.

例3已知整数对排列如下:(1,1), (1,2), (2,1), (1,3), (2,2), (3,1), (1,4), (2,3), (3,2), (4,1), (1,5), (2,4), …则第60个整数对是______.

解将整数对中数字之和相等的排在同一行,并按从小到大“竖起”排成如下“三角形数阵”.

(1,1)

(1,2) (2,1)

(1,3) (2,2) (3,1)

(1,4) (2,3) (3,2) (4,1)

… ………………

由此推知,第n行为(1,n)， (2,n-1)， (3,n-2)， (4,n-3)， …，(n,1).

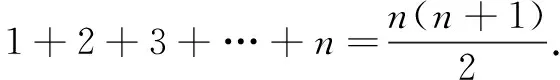
设第60个整数对在第n+1行，则有

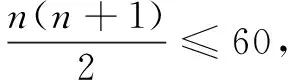
由此易知，前10行共有55个整数对.故第60个整数对为第11行第5个整数对,按上面“三角形数阵”的排列规律可知:第11行的整数列依次为(1,11),(2,10),(3,9),(4,8),(5,7). 因此，第60个整数对为(5,7).

如果我们将“三角形数阵”中的数字换成图形,可以类似地处理.再看下列例子.

例4一同学在电脑中打出如下若干个圆(图中●表示实圆,○表示空心圆):●○●●○●●●○●●●●○●●●●●

○●●●●●●○…,若将此若干个圆依此规律继续下去得到一系列圆,那么在前2 004个圆中有______个空心圆.

解将圆依次“竖起”排成如下“梯形图阵”,且每行以实圆开头.

● ○

● ● ○

● ● ● ○

● ● ● ● ○

● ● ● ● ● ○

… …………

由此推知,第n行为 ●●●●…●○ (共n+1个圆).

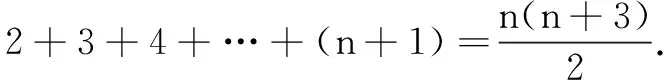
故在前2 004个圆中有 61个空心圆.