一道课本习题的多种证明与推广

杨瑞柯

(安徽省芜湖市安徽师范大学附属中学高一(13)班，241000)

题目(人教A班选修4-5(不等式选讲)第29页习题4)设x、y为正数,且x+y=1,证明:

①

一、证法展示

证法1基本不等式法

评注基本不等式是不等式证明的最基本工具，合理拼凑是使用该工具的基本技能.

证法2倒代换法

评注通过倒代换将分式转化为整式，再结合条件简化整理，是降低不等式证明难度的有效途径.

证法3“1”代换法

原不等式成立．

评注巧用“1”代换与配对原理解题，激发了我们创作的灵感，增强了解题的趣味性.

证法4三角换元法

由x+y=1联想到sin2θ+cos2θ=1,可设x=sin2θ,y=cos2θ,则

从而原不等式成立．

评注用三角换元进行证明，让我们感受到了数学不同知识模块之间存在着广泛的联系，彰显了数学知识的博大精深.

二、问题的推广

1.指数推广

推论1设x、y为正数,且x+y=1,则有

②

推论2设x、y为正数,且x+y=1,n∈N*(n≥2),则有

③

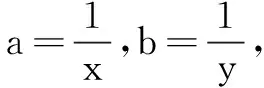
(a+b)n-(an+bn)≥22n-2n+1.

④

不等式(4)即为1988年全国高中数学联赛题,用数学归纳法易证明结论成立.(限于篇幅，此处从略)

2.项数推广

推广3设x1,x2,…,xn均为正实数,且x1+x2+…+xn=1,n∈N*,n≥2,则有

≥(n2-1)n.

⑤

将上述n个不等式相乘，即得不等式⑤,故结论成立．