考虑毛细水负压力引起坑外场地沉降量计算方法和潜在威胁性研究

2020-04-22周爱兆隋晓岚

科学技术与工程 2020年2期

周爱兆, 胡远, 隋晓岚

(江苏科技大学土木工程与建筑学院，镇江 212003)

随着基坑开挖深度的不断增大，不合理的基坑降水开挖对周边环境影响较大。然而相关人员基坑支护设计时，对基坑周边环境影响考虑较少，由此而导致周边建筑物产生不均匀沉降的例子屡见不鲜，对人类财产及人身安全造成极大威胁。因此，在基坑工程设计与施工过程中，在确保基坑内施工环境安全同时，还应该最大程度减小对周边环境影响[1-2]。

目前针对基坑降水对周边环境影响方面研究，多从孔隙水压力与有效应力变化关系方面入手，即基坑内降水使坑外水位下降，坑外土体孔隙水压力降低，有效应力增大，使土体产生压缩变形。Shen等[3]基于三维地下水渗流和一维太沙基固结理论建立地面沉降计算的数值模型，通过与地面实测沉降比较证明其合理性，并通过该模型预测上海地区未来30年沉降发展趋势。龚晓南等[4]针对顶板完全隔水的承压水层，基于完整井理论提出反映承压水降压作用的附加压力公式，在Mindlin解基础上，推导出承压水降压作用附加分布力作用下的地面沉降公式，并讨论了上覆土层厚度、上覆土层弹性模量、承压水水头降深和承压层导水系数对沉降影响。左德祥[5]以徐州某地铁车站降水减压施工为例，分析了降低潜水、深层承压水对基坑周围地面沉降的影响程度范围，提出了沉降控制措施，为类似工程提出勘察、设计及施工监测方面建议。现有研究多是在总应力不变的前提下展开，鲜有考虑总应力之外的力——毛细水压力。

现从基坑内降水对坑外水位影响规律入手，借助海森(Hazen A)经验公式计算毛细水上升高度及其产生的负压力，并且在规范给出的分层总和法计算土体沉降的基础上，提出考虑毛细水负压力作用计算土体沉降量简化方法。利用该方法研究在不同孔隙比、有效粒径情况下，毛细水上升规律，及其产生的负压力对土体沉降影响性，为相关人员计算坑内降水导致坑外土体沉降提供参考。

1 考虑毛细负压力的坑外土体降水沉降计算方法

1.1 基坑内降水导致坑外地下水位变化规律

基坑降水引起周边地下水变化情况与库水位下降情况相似，故借鉴库水位下降时水位面计算方法[6-7]，如图1所示，止水帷幕高度为H，原地下水位距地面高度为H0，则坑外距离x处，地下水位差h(x)为

(1)

μ=1.137(1+e)0.000 117 50.067(6+lgk)

(2)

式(2)中：e为土体孔隙比；K为渗透系数，cm/s。对于非均质土采用水平方向的等效渗透系数Kx，按式(3)计算得到：

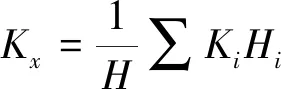
(3)

式(3)中：H表示降水影响范围内土层总厚度，m；Ki、Hi分别表示第i层土的渗透系数(m/d)与厚度，m。

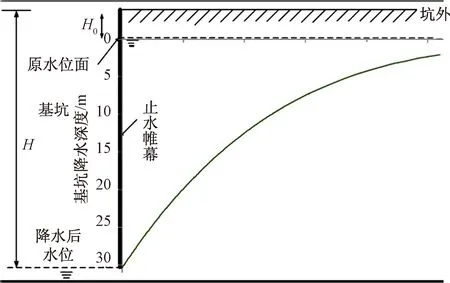
图1 基坑外水位变化示意图

1.2 水位下降后考虑毛细水负压的有效应力计算

1.2.1 毛细水负压产生的有效应力

当前对基坑内降水对周边环境影响研究，多着力于有效自重应力变化导致土体变形方面。即总应力保持不变，随着孔隙水压力不断降低，有效自重应力不断增大，从而导致周边土体压缩变形。以地下水位从地表下降的均匀土层为例，如图2(a)、图2(b)所示，降水前△OGB、△OGA、△OGC分别表示土体有效自重应力、孔隙水压力和总应力随深度的变化情况，其中S△OGC=S△OGA+S△OGB。降水后，水位从O点降到O′点，孔隙水压力由△OGA减小为△O′GA′，有效自重应力从△OGB变为OGB′F，则图2(b)中OBB′F表示有效自重应力增量。

上述分析并未考虑毛细水压力对土中有效应力的影响，毛细水上升的本质即土中水在基质势作用下上升转化为重力势能的过程[8]，如式(4)所示。对有些土体而言，土中水基质势较大，其转化为毛细水负压力对土体压缩变形的影响是不可忽略的。如图2(c)所示，地下水位从O点下降到O′点后，在表面张力作用下O′处毛细水上升至H处，形成高度为HO′的毛细包水带。以△O′HD表示O′处毛细水负压，为了便于直观分析，从F作JE=DH使得△FEJ所表示的力数值上等于毛细压力，图2(c)中△FEJ表示毛细水负压力，虚线部分即表示因坑内降水对坑外场地产生的总体附加有效应力。

W重=-W基=-γwh

(4)

式(4)中：W为总势能；W重为重力势能；W基为基质势；γw为水重度；h为毛细水上升高度。

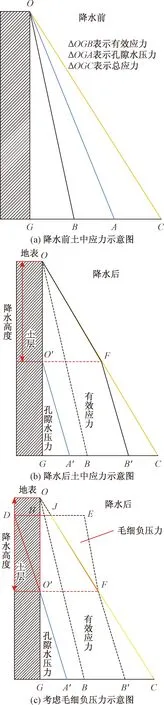
图2 降水前后土中应力变化图

1.2.2 毛细水的上升高度

根据上述毛细水负压产生有效应力的分析可知：计算毛细水负压产生的有效应力的关键是稳定水位面之上，土体中毛细水的上升高度。李广信等[9]通过水柱静力平衡条件推导出毛细水上升高度计算公式，如式(5)所示，式(5)表明，毛细水上升高度与毛细管半径成反比，毛细管径越小，即土颗粒直径越小，毛细水上升高度越大。

(5)

式(5)中包含了毛细管半径r参数。对于天然土体中的孔隙结构复杂，并不能直接采用毛细管来描述。为了便于工程运用，毛细水产生的负压，可采用海森(Hazen A)经验公式进行估算[10]：

(6)

式(6)中：hc表示毛细水上升高度，m；e表示土的孔隙比；d10表示土的有效粒径，m；C表示系数，与土粒形状及表面洁净情况有关，C=(1～5)×10-5,m2。

1.2.3 总有效应力计算方法

(1)有效自重应力计算。基坑内降水，导致坑外场地地下水位下降，产生有效应力包括土体有效自重应力增量与毛细水负压力。土体中总应力保持不变，其有效自重应力增大量即土体中孔隙水压力减少量，如图3橙色线条部分所示，有效自重应力随着水位降深的增加而增大，二者呈正比关系，计算方法为

(7)

式(7)中:hi为第i土层的厚度,m;Δγi为相应土层的有效重度增量,kN/m3，m为h(x)范围内土层。

(2)毛细水负压力计算。毛细水负压力的计算为一个分段函数，如图3蓝色线条部分所示(红色加粗部分表示共同增长部分)，当水位降深H小于毛细水上升最大高度hc时，毛细水高度按水位降深高度计算，其增长趋势与有效应力增长趋势相同；当水位降深大于毛细水最大高度时，毛细水高度即毛细饱和区高度，此时毛细水负压力达到最大值，具体计算方法为

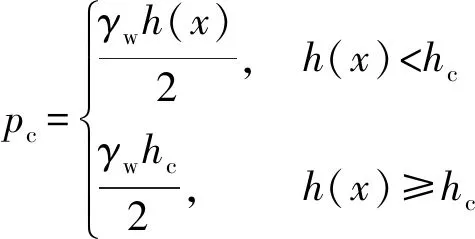
(8)

二者计算结果之和为总附加应力：

σ=Δσ′z+pc

(9)

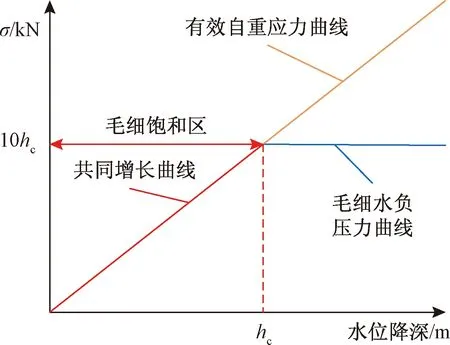
图3 降水后土体附加应力示意图

1.3 附加应力产生沉降量计算

目前，《建筑地基基础设计规范》推荐使用分层总和法对地基沉降量进行计算[11]，地基总沉降量等于成层土沉降量总和，如式(10)、式(11)所示。

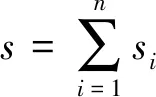
(10)

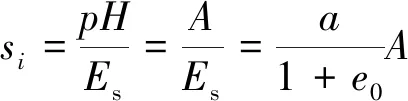
(11)

式中：s为地基土总沉降量；si为第i层土沉降量；p为作用于土层厚度范围内的平均附加应力；H为土层厚度；A为作用于土层厚度范围内附加应力分布图面积，A=pH;Es为侧限压缩模量；a为压缩系数；e0为初始孔隙比。

将式(8)代入式(11)可计算出毛细负压力对土体压缩量，用式(12)所示。将该部分沉降量与分层总和法计算的土体有效自重应力产生的沉降量相加，最终确定基坑周边土体沉降量S总。

(12)

(13)

2 毛细水负压力产生额外沉降威胁性分析

毛细水负压力的大小取决于土体中毛细水上升的高度，由式(6)可知，毛细水上升高度与土体有效粒径及孔隙比有关。本节通过对比分析孔隙比与粒径的变化对毛细水上升高度的影响，进而对其相应的潜在威胁性进行阐述。其中当土体有效粒径小于0.005 mm时，土中细粒含量高，塑性指数大，土粒中结合水膜较多，毛细水上升通道被阻断[12]，情况较为复杂，此处暂不予考虑。

2.1 孔隙比变化对毛细水上升高度及土体沉降量影响

取孔隙比为0.96、0.87、0.7、0.659、0.59，粒径为0.005 mm，侧限压缩模量为9.2 MPa的土体进行研究，将上述数据代入式(6)，计算结果如图4所示(C一律取4×10-5m2)。如图4所示，当土体孔隙比为0.59时，毛细水上升高度为13.55 m，且随着孔隙比的不断减小，毛细水上升高度不断升高，二者间相互关系近似于线性变化。

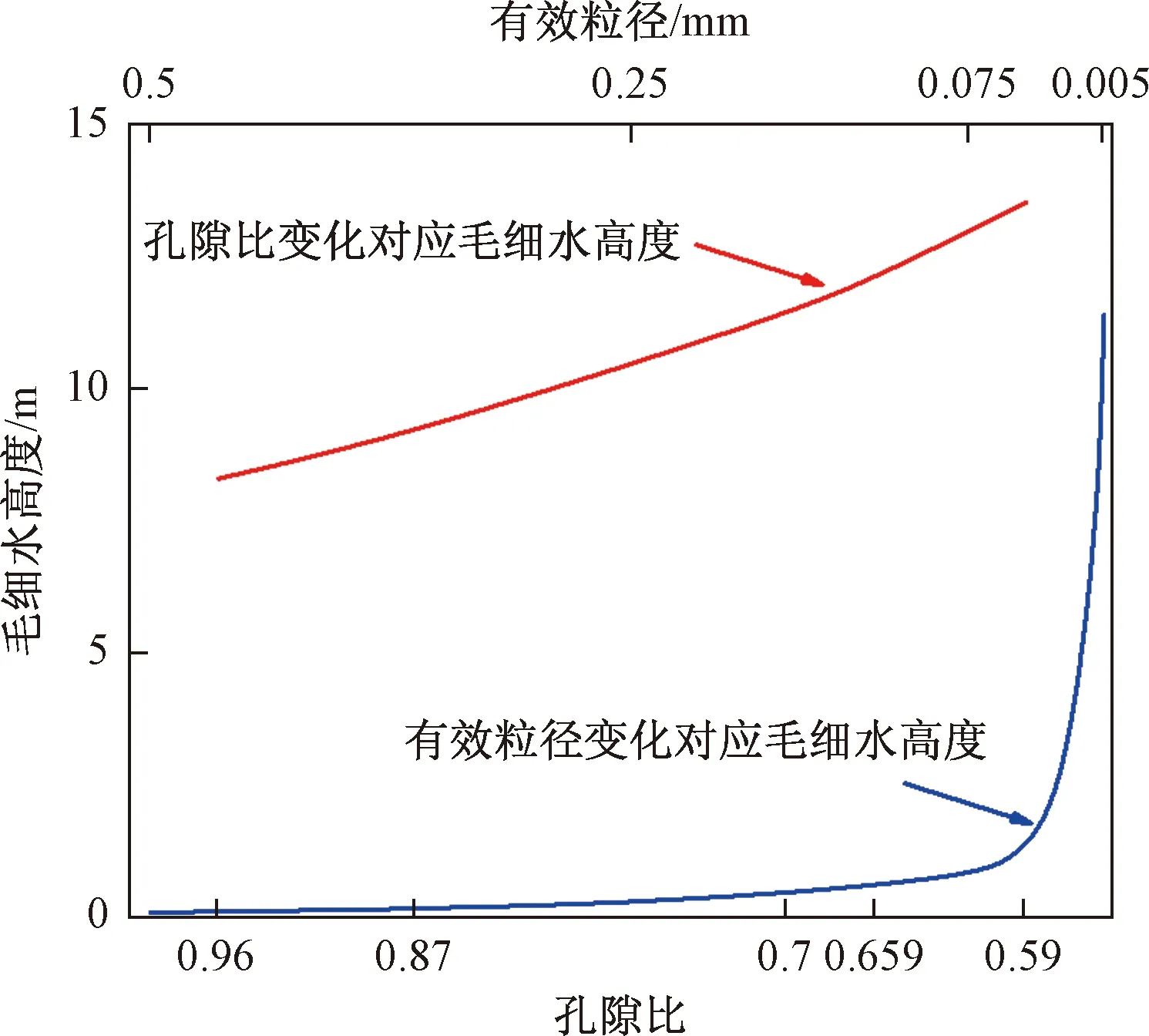
图4 毛细水上升高度与相关参数关系

假设有15 m厚土层，原地下水位为地下1 m，现将水位降至土层底部，计算土体在不同孔隙比情况下，有效应力增量产生土体沉降量及考虑毛细水负压力的附加应力产生的土体沉降量，结果如图5所示。有效应力增量产生土体沉降受孔隙比影响较小，水位降深14 m后，有效应力增加量所产生的最大位移为10.65 mm。当考虑毛细负压力作用时，随着孔隙比的减小，毛细水最大上升高度不断增加，附加应力不断增加，其产生的土体变形也在不断增加。当孔隙比为0.59时，考虑毛细水负压力作用所产生的土体沉降量最大，其值为20.97 mm接近有效应力产生沉降量的两倍。二者差值即为毛细水负压力作用产生的土体附加沉降量。从图5中可明显看出，随着孔隙比不断减小，毛细水负压力产生土体沉降量不断增大。当孔隙比为0.59时，毛细水负压力值产生位移与有效应力产生位移基本相同。此时，考虑毛细负压力影响计算得到土体沉降量接近仅考虑有效应力增量作用产生沉降量的两倍。

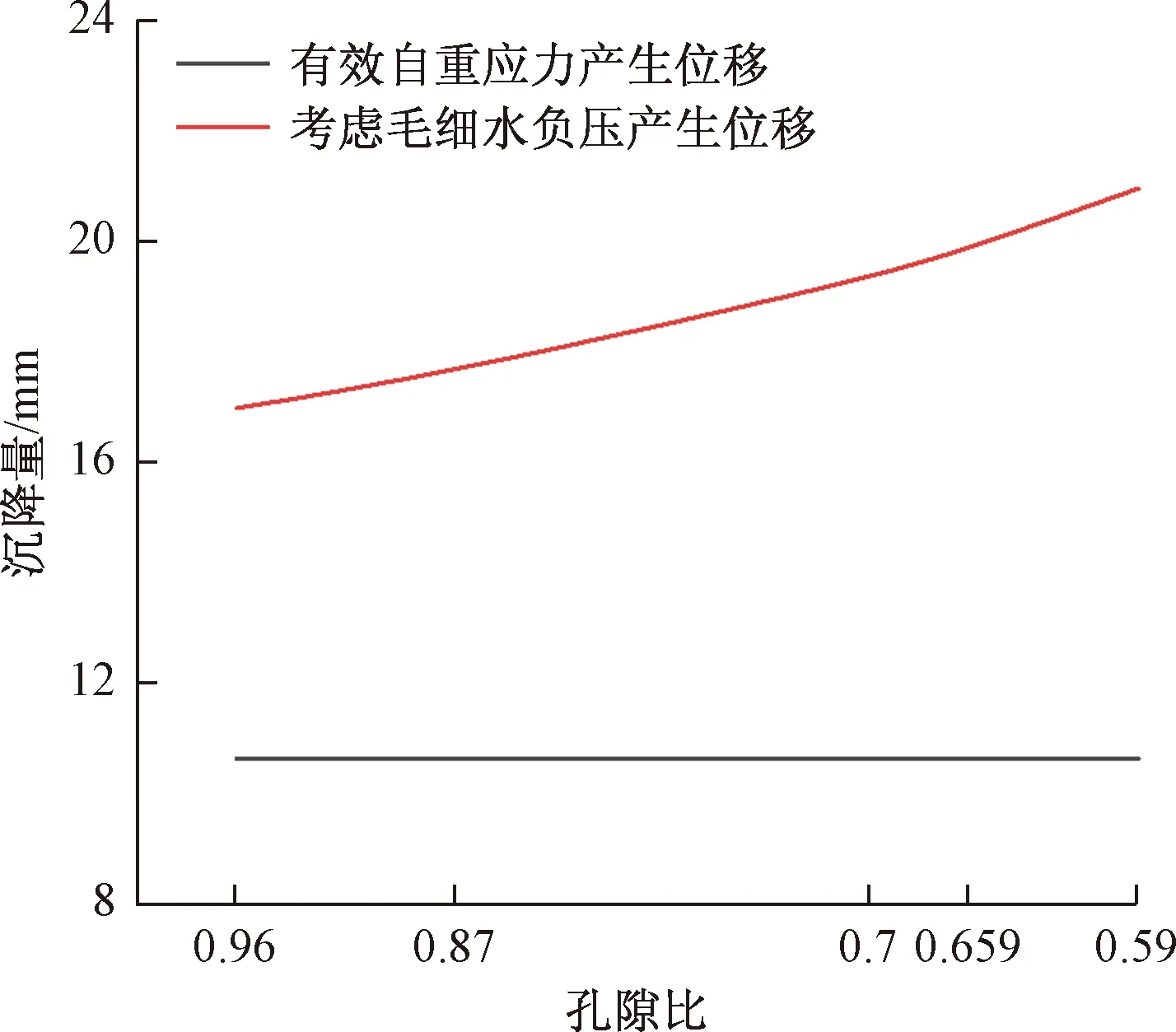
图5 降水后土体产生位移与孔隙比关系

2.2 土体有效粒径变化对毛细水上升高度及土体沉降量影响

取有效粒径为0.5、0.25、0.075、0.005 mm(分别对应粗砂、中砂、细砂、粉土最小粒径[8])，孔隙比为0.7进行研究，将上述数据代入式(4)计算得出结果如图4所示。如图4所示，当有效粒径为0.005 mm时，毛细水上升高度最大为11.42 m。且毛细水上升高度随着有效粒径的减小而不断增大，有效粒径从0.5 mm变化至0.075 mm时，毛细水上升高度变化趋于缓慢，有效粒径从0.075 mm变化至0.005 mm时，毛细水上升高度变化出现陡增趋势。

同样假设有15 m厚土层，原地下水位为地下1 m，现将水位降至土层底部，在不同有效粒径情况下，分别计算土体有效应力增量产生的沉降量与考虑毛细水负压力的附加应力产生的沉降量，为了便于分析，所取土体侧限压缩模量均取9.2 MPa，计算结果如图6所示。随着土体粒径不断减小，附加应力产生的位移量不断增加。从图6中可明显看出，当土体有效粒径处于0.075～0.5 mm时，考虑毛细水负压力作用所产生的沉降与有效应力增量产生沉降，最大相差0.58 mm，相对于整体沉降量其值较小，所造成的附加沉降可控。当土体有效粒径小于0.075 mm时，毛细水负压力产生位移值最高可达到8.7 mm，其值接近有效应力增量产生位移量，且随着土体粒径减小，毛细水负压力产生的附加沉降还在继续增大。上述规律表明，当土体有效粒径处于0.005～0.075 mm时，应考虑毛细水负压力对土体压缩变形影响。

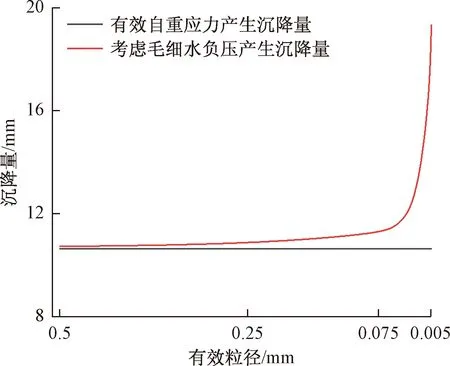
图6 降水后土体产生位移与有效粒径关系

图7 附加应力随水位降深变化图

2.3 水位降深对毛细水负压力影响

水位降深导致土体内部附加应力增加示意图如图7所示，当水位降深H小于最大毛细水高度hc时，毛细负压力分布形式与有效应力相似，但增大方向相反，毛细水负压力值随着毛细水上升高度的增加而增加，最大值出现在毛细饱和区顶部。当水位降深H等于最大毛细水高度hc时，毛细水负压力达到峰值，不再随水位降深增大而增加。当水位降深H大于最大毛细水上升hc时，有效应力增量继续随着水位降深的增大而增加，而此时毛细水负压力值不再变化，但由于毛细水负压力作用范围为稳定水位面向上至最大毛细水上升高度，故其作用范围随着水位降深的不断增加而整体下移。

由于毛细水负压力的存在，上部土体附加应力明显增加。随着土体埋深的增加，土体自重应力不断增加，上部土层有效应力小于下部土层有效应力。对于稳定场地内土层，土体压缩模量从上至下总体呈递增趋势，上部土层可压缩量总体大于下部土层压缩量。因此，即使产生的毛细水负压力与有效应力增加量相等，毛细水负压力对土体沉降的影响也大于有效应力增加值对土体的影响。当毛细饱和区内存在压缩性较强的软土时，上述情形表现的更为明显。