单方柱绕流的直接数值模拟
2020-04-22陶善聪郝克理
陶善聪, 郝克理, 周 毅
(南京理工大学能源与动力工程学院,南京 210094)
绕流运动是指流体绕物体外部的流动。在日常生活和工程应用中常见此类问题,如气流吹过建筑群、海水流过海洋平台等。由于边界层的分离,固体表面会有漩涡交替生成、脱落、发展和消亡。当漩涡脱落频率与固体障碍物自振频率一致时,易产生共振而对物体自身造成损毁,因此研究绕流问题意义重大。由于方柱绕流的分离点固定,且制造工艺和网格生成简便,因此方柱被广泛用于研究绕流问题。
近年来,众多学者对方柱绕流问题开展了广泛研究。外国开展此类问题研究起步较早。Lyn等[1]通过激光多普勒测速仪定量分析单方柱绕流(雷诺数Re=21 400)的湍流统计特性,精确的实验结果成为后续学者验证实验和数值计算结果的依据。实际流动是非稳态的,Kurtulus等[2]通过粒子图像测速仪研究单方柱在Re=4 900下的非稳态气动力,指出无黏流下的非稳态项可以忽略且二维流动下的非稳态气动力可以通过时间分辨粒子图像测速(time-resolved particle image velocimetry,TR-PIV)精确测量。最近许多研究结果表明Kolmogorov的论述并不完全适用,-5/3能谱幂次规律同样可以在非均匀和各向异性的剪切流或边界层中出现。Portela等[3]利用KHMH(Kármán-Howarth-Monin-Hill)方程研究绕流单方柱下游的能量传递行为,发现非均匀和各项异性湍流区出现的-5/3能谱伴随着能量反向串级行为的发生,证实在剪切流或边界层中能量不仅由大尺度湍涡向小尺度湍涡传递且存在由小尺度湍涡向大尺度湍涡传递。钝体绕流问题涉及到湍流流动的不稳定性,对其进行深入研究能够增强关于流动本质的认识。例如,单方柱绕流的远场湍动能预算[4]、串列并列双方柱[5-6]和三方柱绕流的本质特征等[7]研究均较好地反映出流场特性。工程实践当中,人们关注的是绕流柱体的气动力特性。郜阳等[8]采用大涡模拟方法比较不同阻塞率下二维方柱绕流的整体气动力和表面风压,结果表明侧面及背风面负风压系数和柱体两侧流场特性对阻塞比变化响应明显。杜晓庆等[9]着重探讨了圆角化方形截面柱体的流场作用机理,发现方柱气动力减小和斯特劳哈尔数(St)增大是由尾流宽度减小和旋涡脱落强度削弱造成的。
现拟从单方柱绕流出发,通过直接数值模拟(direct numerical simulation, DNS)方法研究湍流场物理特性。基于快速本征正交分解(snap-proper orthogonal decomposition,Snap-pod)将瞬时流场分解为不同含能尺度结构的模态,定性地分析多尺度涡结构对流场的贡献;借助速度梯度张量不变量(R,Q)和(QW, -QS)联合概率密度函数(joint probability density function, JPDF)探讨流场不同流向位置处的湍流场特性。
1 数值方法
直接数值模拟方法的控制方程为连续性方程和不可压缩Navier-Stokes方程组,张量表达式如下:
(1)
(2)
式中:u为速度;ρ为密度;P为压力;υ为运动黏度;t为时间;X、Y、Z分别为流向、法向和展向方向。
流场布置如图1所示,X、Y、Z方向对应的域长分别为LX= 18T0,LY= 16T0,LZ= 16T0,T0为方柱流向和法向尺寸。方柱中心布置在距离入口Xbar= 8T0处,入口雷诺数为Rein=UinT0/v=1 200,其中Uin为入口流速,为3.75 m·s-1。阻塞率σ=T0/LY×100%= 6.25%,各方向网格量分别为NXNYNZ=421×337×337。具体计算参数见表1。入口和出口边界条件采用Inflow/Outflow,法向和展向采用周期性边界条件。时间递进采用三阶Runge-Kutta方法求解,对流项采用四阶中心差分求解,采用六阶中心差分紧致格式(X方向)和谱方法(Y、Z方向)求解黏性项,压力项通过泊松方程求解。方柱模型采用浸入式边界法。为精确模拟边界层附近的小尺度运动,方柱附近沿X方向采用函数加密,网格布置及其加密示意图如图2(a)、图2(b)所示。
2 数值方法验证
方柱绕流某一瞬时涡量场如图3所示。从图3中可以清晰地看到旋涡分别从方柱上下表面脱落而向下游发展,在下游形成交替的涡街。图4给出了流场网格的空间分辨率。可以看出,流场中最大空间分辨率为(ΔXΔYΔZ)1/3/η=3.3,表现在X/T0=2.1左右,方柱下游出口段空间分辨率最小,其值为(ΔXΔYΔZ)1/3/η=2.3。其中η为Kolmogorov长度尺度,是湍流场中的最小尺度。Laizet等[10]指出,当流场空间分辨率小于5时,利用DNS求解一阶及二阶动量的结果与实验相比误差不超过5%,因此计算精度满足空间分辨率要求。图5(a)、图5(b)分别展示了中心线上不同位置处(X/T0=2, 4, 6, 8)流向和法向速度脉动能谱在频域的变化。可以看到,流向和法向速度脉动能谱在频域演化趋势一致,但峰值点对应的fT0/Uin不同(f为取样率)。法向脉动能谱极值点为fT0/Uin=0.14,等于单方柱绕流的漩涡脱落频率斯特劳哈尔数(St)。流向速度脉动能谱极值点fT0/Uin=0.28为漩涡脱落频率St的两倍。图6为St与Davis等[11]的实验结果对比,结果基本吻合。
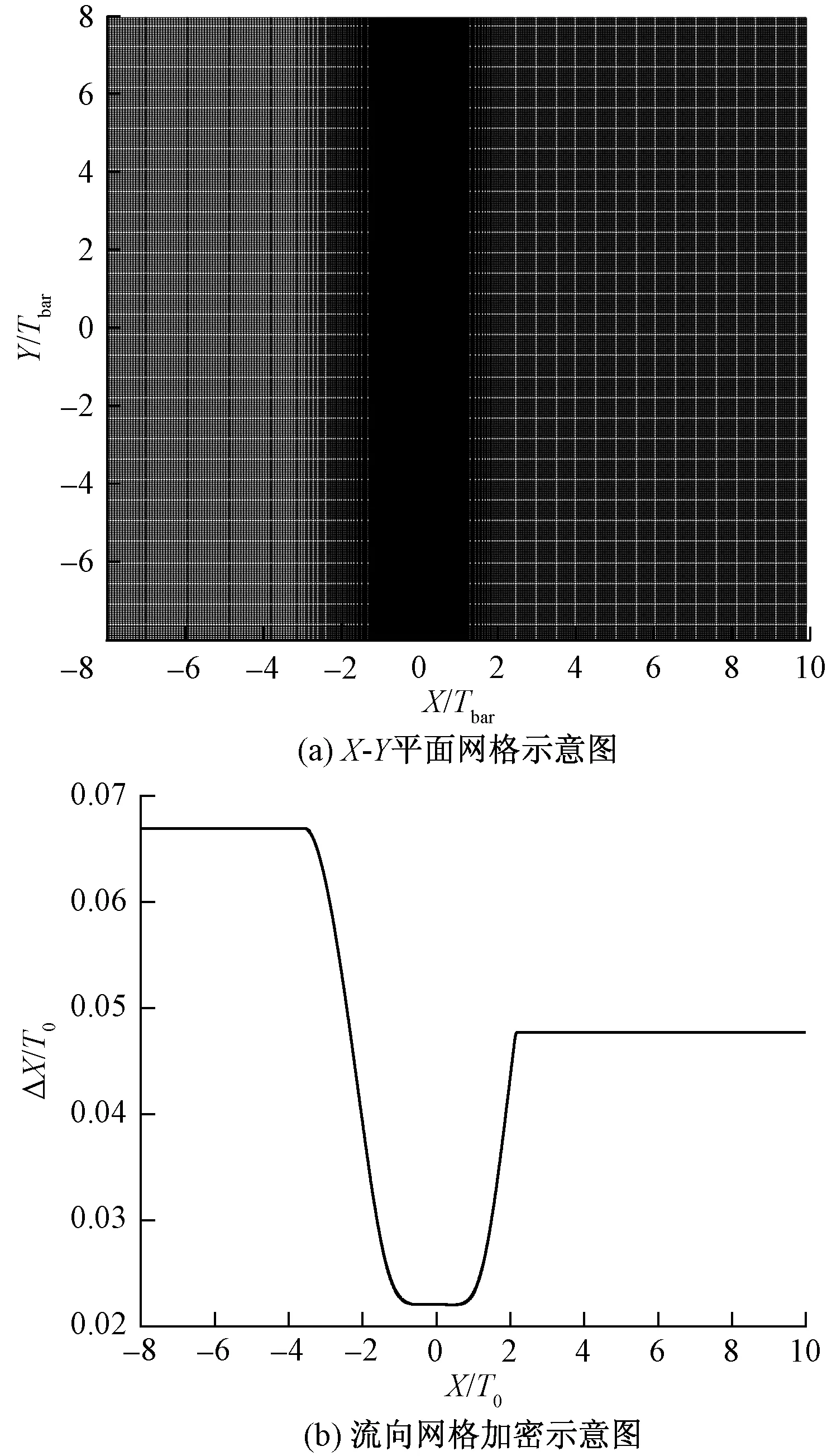
图2 网格及加密示意图

图3 瞬时涡量云图
图7、图8分别给出了时均流场流向速度与表面压强系数分布,其中黑色空心方框表示方柱模型。
由于各实验布置条件有所差别,最大回流速度略小于Hu等[12]、Lyn 等[1]和Durao 等[13]的计算结果,恢复速度与低雷诺数下实验Lee等[14]结果非常吻合,而方柱表面压强分布与Chen等[15]实验结果较为接近。演变趋势与Bearman等[16]和Mizota等[17]相同。综上所述,数值模拟结果与前期实验相吻合。

图4 空间分辨率的流向演变示意图

图5 速度脉动能谱
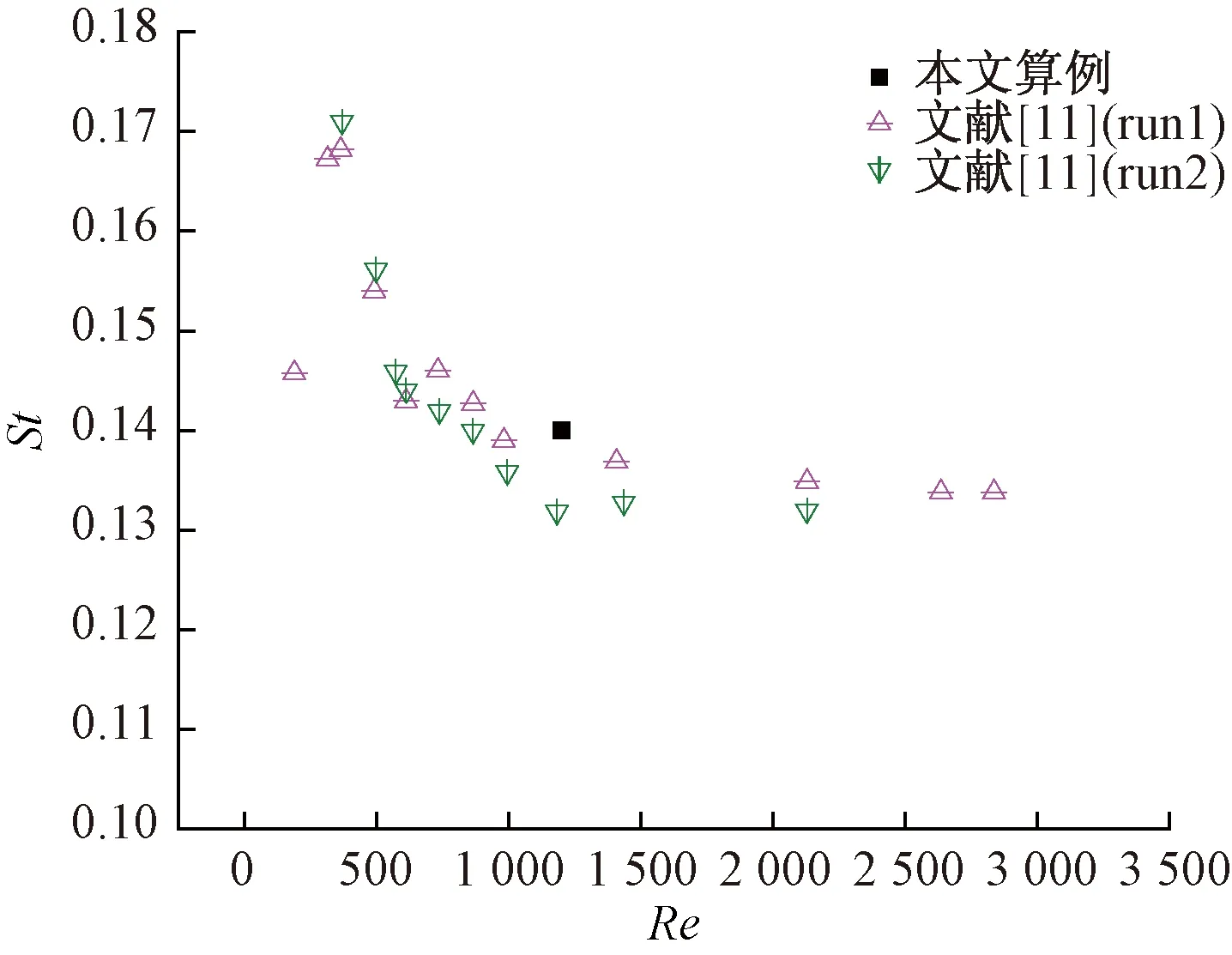
图6 斯特劳哈尔数(St)与实验对比

图7 中心线上平均流速
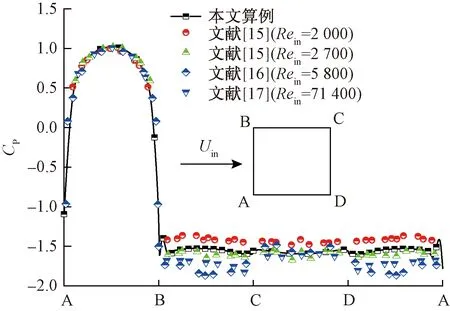
图8 方柱表面压强系数
3 结果分析与讨论
3.1 快速本征正交分解
现通过快速本征正交分解方法将某一时刻的流场分解为具有不同漩涡特征的r个模态以对比分析方柱绕流场中的相干结构。其基本思想是,通过包含N(1, 2, …,N)个时间步流场的矩阵U求解相关矩阵C,再找出前r个模态φ,这r个模态累积的能量基本等效于全空间的总能量。具体求法如下。
通过相对能量ε(r)的大小确定模态个数r的取值:
(3)
式(3)中:λi是时间相关矩阵C的特征值从大到小的排列。
再计算每一模态:
(4)
最后通过每个模态的系数α重构原始流场。
(5)
(6)
相关矩阵特征值λ与相对能量ε随模态r的累积如图9所示。由图9可知,前50个模态累积的能量达到总能量的99.99%。故提取前50个模态重构任意时刻流向速度场,该时刻重构流场与原始流场对比如图10所示。不难发现,前50个模态基本已提取到原始流场全部的流向速度细节,也侧面验证了所用方法的准确及精确性。由于利用本征正交分解(proper orthogonal decomposition,POD)分解速度场,因而第一阶模态代表平均速度场的特征,剩余模态对应分解脉动速度场的特征。前五模态的速度等值线图如图11所示。第一阶模态沿Y/T0=0对称分布,柱体上下表面附近产生加速区而回流区在柱体下游生成,这表明流动随时间呈现周期性变化。第二和第三阶模态沿Y/T0=0表现出反对称分布,而沿流向生成正负交替的涡街。值得注意的是,第三阶模态从位置和形状来看类似于第二阶模态涡街的“成长”。第四和第五模态速度等值线图与前三个模态相比更加紊乱,小尺度旋涡充满整个流场,且与文献[18]的结果存在较大出入。这可能由于文献[18]模拟的是Re= 100的二维层流工况,无法提取湍流场中的多尺度旋涡结构。
第二、第三、第四、第五阶模态的系数α随时间演化分别如图12和图13所示。图12中第二、三阶模态系数随时间呈现出正弦函数演变,且脱落周期为St1=1/(t2-t1)=1/(t4-t3)≈0.14,恰好等于图5所求的St,这更加证明第二、三阶模态提取的是流场大尺度旋涡脱落特征。图13中第四、五阶模态的旋涡脱落周期显然小于第二、三阶模态流场中的旋涡脱落周期,结合速度等值线图可知这两个模态提取的是流场中的高频小尺度旋涡。图14给出了(第二、第三)和(第四、第五)模态系数的利萨如图形。模态系数的分散程度实际上代表大尺度相干结构的周期性强弱,显而易见第二、第三模态周期性更强。且利萨如图圆形分布半径的平方与前两个模态对总能量的贡献成正比,表明小尺度运动(第四、五模态)蕴含的能量较弱。
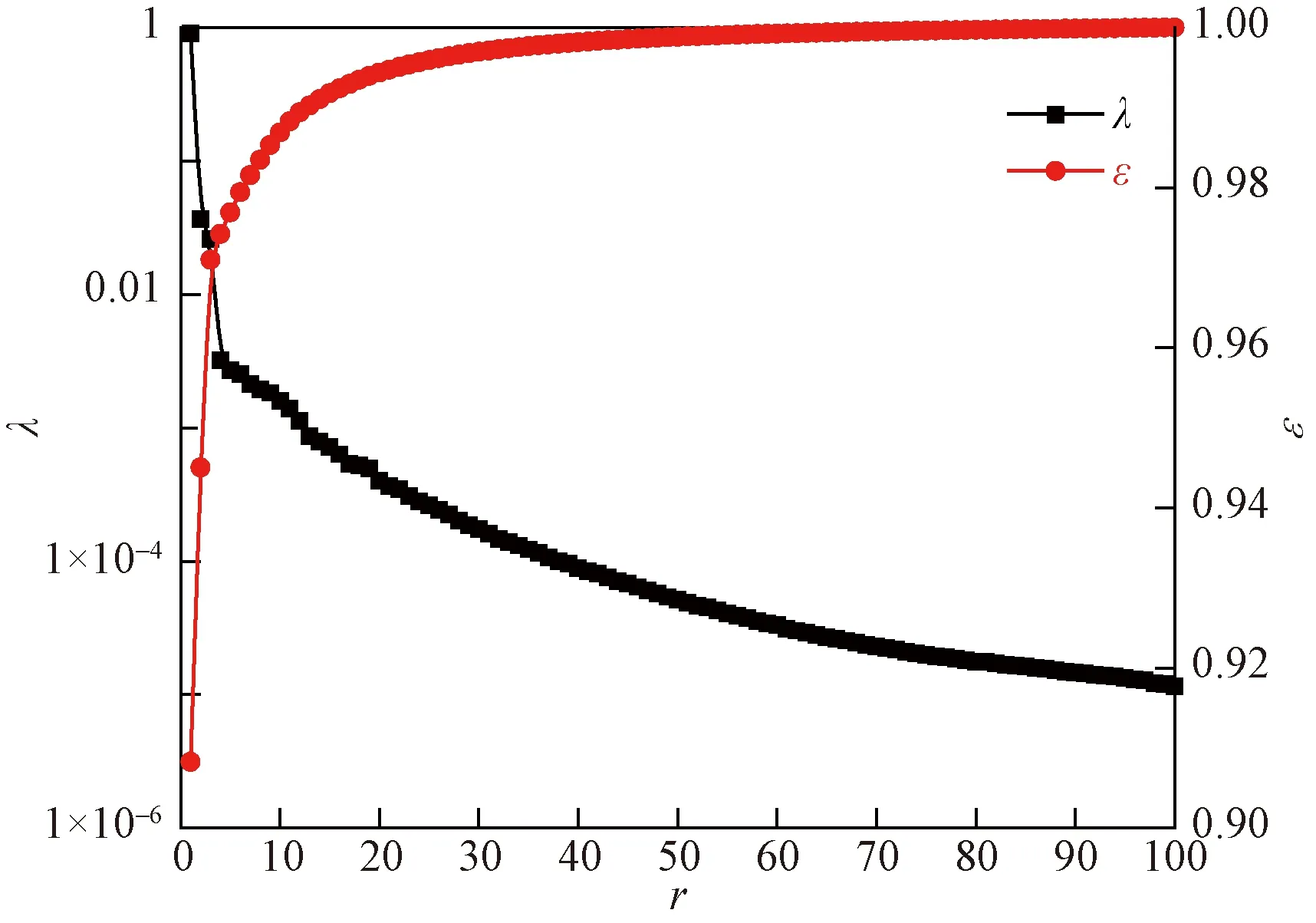
图9 相关矩阵特征值λ与相对能量ε随模态r的累积

图10 原始流场与重构流场对比

图11 各模态流向速度等值线图

图12 第二、第三模态系数随时间演变
3.2 速度梯度张量不变量
速度梯度可定义为
(7)
式(7)中:V0为初始速度;V为终止速度。
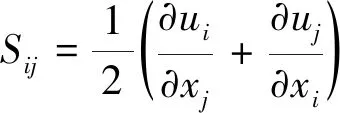
速度梯度张量的特征方程为
(8)
式(8)中:λi为速度梯度张量的特征值;第一不变量P、第二不变量Q和第三不变量R可表达为
P=-Si
(9)
(10)
(11)
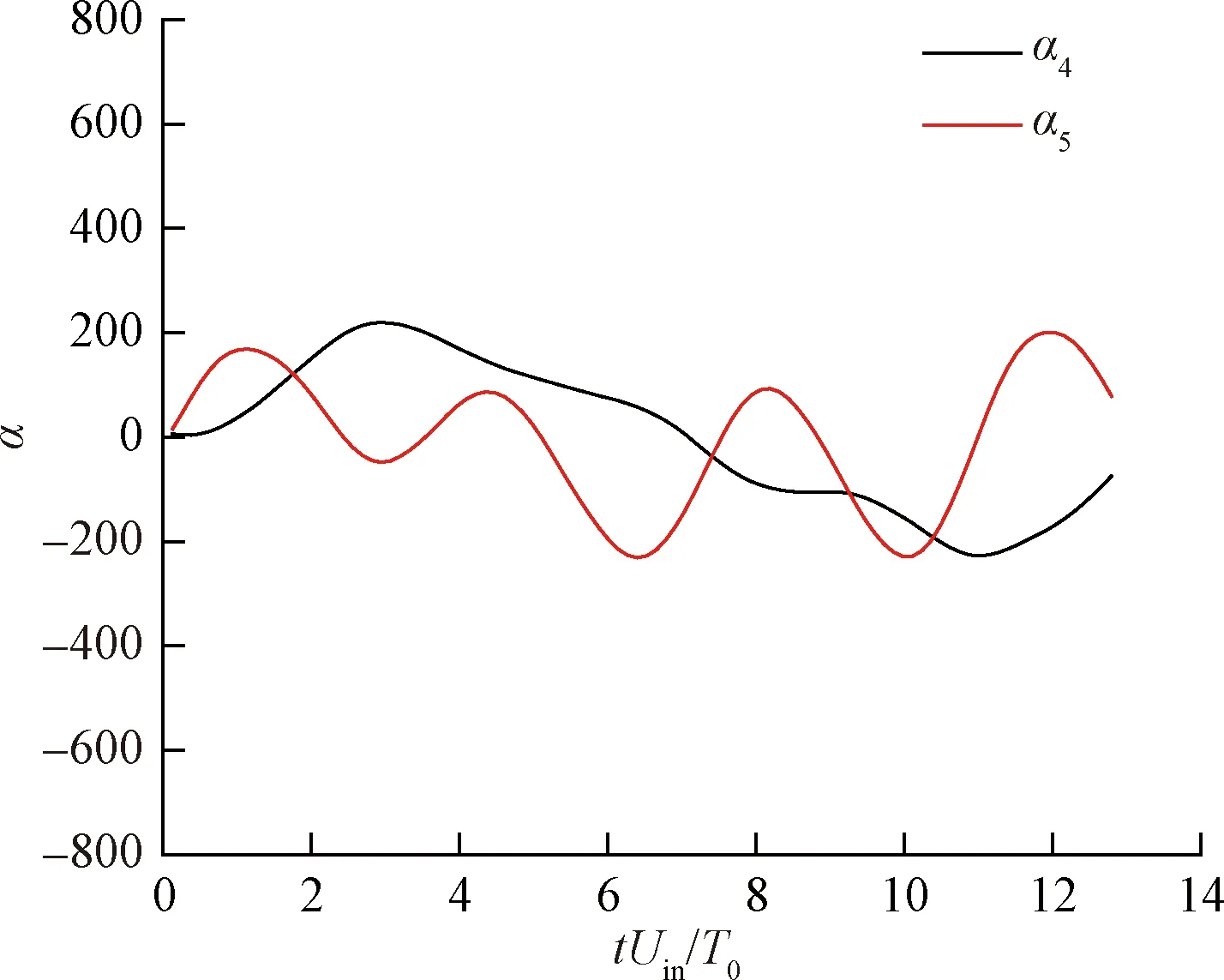
图13 第四、第五模态系数随时间演变

图14 模态系数利萨如图

图15 (Q , R),(-QS,QW) 拓扑图[19]

图16 各流向位置(Q, R), (-QS,QW) JPDF云图

4 结论
采用直接数值模拟方法研究Re=1 200的单方柱绕流特性,通过将斯特劳哈尔数、平均流速和表面压强系数与文献中结果[11-17]对比,验证数值方法的正确性。进一步采用本征正交分解方法提取湍流场中不同尺度结构,分析相干结构对湍流流动的贡献。最后借助(R,Q)和(QW,-QS)联合概率密度函数探讨流场不同流向位置处的湍流流动机理,结论如下。
(1)对于速度场的模态分解,第一模态代表平均速度场的特征;第二、第三阶模态提取的是流场中的低频大尺度旋涡特征;第四、第五模态提取的是流场中的高频小尺度旋涡特征。第二、第三模态均有强周期性且蕴含了大部分流场能量。
(2)通过对速度梯度张量的第二不变量Q和第三不变量R的分析,柱体下游大致可分为两个流动阶段:发展阶段(X/T0=0.51-1.9),流体以涡流层结构和耗散作用为主,涡流管结构逐渐生成;成熟阶段(X/T0=1.9-9.0),流场中湍流结构高涡量拟能和高能量耗散率并存。
