基于趋势特征聚类的多元相似时间序列的提取
2020-04-22王建东韩邦磊
解 初, 王建东, 韩邦磊, 王 振
(山东科技大学电气与自动化工程学院,青岛 266590)
在现代的工业生产中,安全问题已经成为不可忽视的重大问题。报警系统在保障工业生产安全等方面起到了至关重要的作用,但是在过程化的工业系统中,生产设备较多,变量与变量之间联系密切,一个变量的变化会受到多个变量的影响,操作人员无法快速准确地找到报警根源,不能及时处理异常状况,导致重大安全事故的发生。
报警根源分析已经成为中外工业界和学术界广泛关注的热点问题[1-3]。Wen等[4]基于集合覆盖理论和精细遗传算法,提出了一种新的电力系统报警处理方法。Simeu-Abazi等[5]利用动态故障树来定位系统中发生警报的故障以滤除故障,但是该方法所用到的参数需要准确地先验知识。马小梅[6]研究贝叶斯网络结构学习算法,并提高了根源分析的效率。上述报警根源分析的方法大都需要相当完整和准确的过程知识。除了机理知识或学习类的算法之外,基于数据驱动捕获变量之间的因果拓扑从而分析变量关系是进行根源分析的另一类方法。Yuan等[7]采用格兰杰因果关系法分析变量之间的因果关系,最终找到根源变量。Hu等[8]通过计算传递熵分析变量之间的因果关系,得到根源变量的传播路径。这几种方法[7-8]假设在一段时间内变量之间的关系是平稳的,不适用于影响因素随时变化的报警根源分析。除以上方法之外,对历史数据进行特征信息的挖掘来辅助进行报警根源分析的工作。张军等[9]使用基于时间序列相似性的多变量时间序列模式挖掘方法,从历史数据中寻找出相似的多变量时间序列。陶少辉等[10]根据历史数据建立主元分析模型(PCA)根据实时数据和PCA模型计算综合指标以在线检测其故障的发生。Bouchair等[11]在历史报警序列中提取故障序列模板,将故障序列模板与新的报警序列进行匹配以进行故障隔离。在进行特征信息挖掘的过程中,中外学者提出了多种相似性查找以及距离度量的方法。Tanaka等[12]提出了基于最小描述长度(MDL)原理的多维数据时间序列主题特征的挖掘算法。肖红等[13]在时间序列分段线性表示基础上,提出一种新的基于趋势转折点的时间序列模式表示方法。陈鹏等[14]采用了一种基于距离和的孤立点挖掘方法来进行分析警情时间序列的异常特征。聚类算法广泛地应用于模式识别以及相似时间序列查找的领域中[15]。王选宏等[16]使用核的模糊C均值对网络数据进行聚类并将该方法用到了数据异常检测中。谢福鼎等[17]基于关键点技术,提出了一种新的时间序列聚类方法。
由于上述方法进行根源分析时需要完整的过程知识或者平稳的变量关系,针对多变量时间序列维度高、数据量大的特点,在趋势提取以及聚类的最新研究基础上,提出了一种基于趋势特征聚类的多元相似时间序列的提取方法。首先对多元时间序列进行分段线性表示,获得它们的趋势特征信息,然后采用密度峰值聚类分析(DPCA)聚类算法[18]对获得的趋势特征在高维空间中聚类,从而实现历史相似时间序列的提取,最后可根据关联变量的变化幅值分析导致主变量发生异常变化的根源变量。用数值仿真和火电机组的工业数据验证了所提方法的有效性。
1 所提方法
1.1 整体思路
在工业系统中,存在容易异常波动甚至会发生报警的关键变量,由于这些变量的异常变化会对工业过程系统产生不利影响,称这些变量为主变量。主变量发生变化时,与之关联的变量也会发生不同程度的变化。
为了解决主变量异常变化的根源分析这一问题,需要对历史数据中主变量出现显著变化的情况进行合理的类别划分,也就是根据不同的数据特征提取相似的时间序列。首先,对主变量和关联变量进行趋势提取;其次,提取分段后各个变量的趋势特征信息;最后,对各个变量的趋势特征进行聚类,从而完成多元时间序列的相似性提取并可以辅助现场工作人员对主变量异常波动的原因进行合理的解释。
1.2 时间序列的趋势提取
对主变量和关联变量提取趋势特征,采用自底向上趋势提取法[19],其主要思想是,通过进行计算拟合误差,合并拟合误差最小的数据段,最终得到设定分段数目的数据段,具体步骤如下。
步骤1产生最准确的拟合数据段,即两个点相连进行拟合,这样第一次迭代将数据段分成m=n/2 段,其中n为数据点的个数。
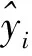
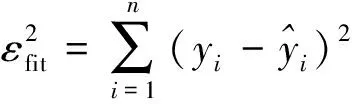
(1)
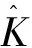
对时间序列进行分段前,需要确定最优的分段数目,采用文献[20]中用凸包的概念确定最优分段数的方法,其中凸包B是变量中一段趋势的边界数据点首尾相连组成的凸多边形,平行四边形A为变量中一段趋势的起始和结束时刻所对应的平行于y轴的直线,以及样本的置信区间的上下限这四条边来形成一个平行四边形。该方法定义一个指标ηi,令ηi=(|A∩B|)/(|A|),即A与B交集的行列式与A的行列式的比值,定义一个指标函数:
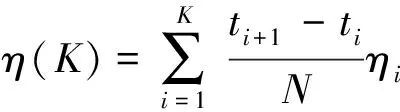
(2)
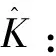

(3)
对主变量进行最优分段数的确定及趋势提取后,用分段线性表示的方法表示时间序列的趋势特征,分段线性表示方法是将时间序列用n个线性方程表示为
x(t)=an+bnt+e(t)
(4)
式(4)中:an和bn表示的是截距和斜率两个参数;e(t)是均值为0,方差为1的高斯白噪声。设数据段的变化时长为Δt,数据段的斜率和变化幅值分别为bn和Δtbn。
以相同的起止点对其他关联变量的数据进行切割分段(设分段数目为n),并对每个数据段进行线性拟合。提取每个变量数据段的变化幅值a和变化时长Δt,并计算变化速率k用于描述该数据段的趋势特征:
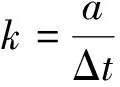
(5)
假设变量数目(主变量和关联变量)总共m个,则n个时间段m个变量的趋势特征可以用n个趋势元组来描述,特征描述如下:
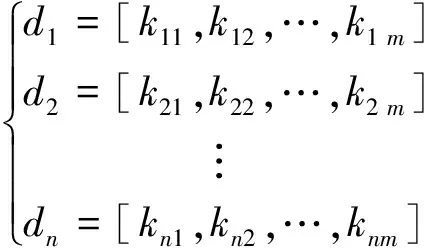
(6)
为了在后续的聚类中使每个变量的量纲保持一致,对上述变量做Z标准化处理,即:
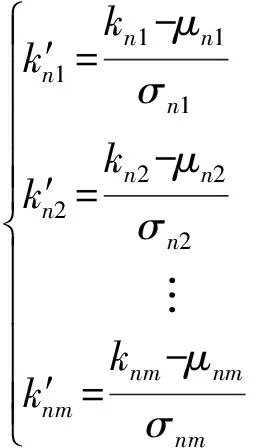
(7)
式(7)中,μnm为第m个变量斜率的均值;σnm为第m个变量斜率的标准差。Z标准化以后的趋势特征元组如下:
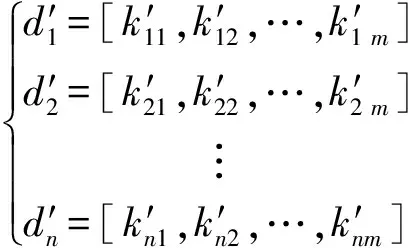
(8)
1.3 DPCA聚类算法
DPCA聚类算法是文献[18]中一个非常有效的聚类分析方法,主要基于以下两个特征。
(1)聚类中心比邻近的点有更高的密度。
(2)聚类中心与其他更高密度的点有更大的距离。
基于以上两个假设,可以主要计算ρi和δi两个量:
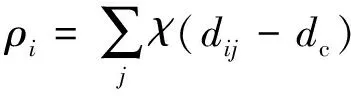
(9)

(10)
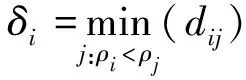
(11)
式中:dc是截断距离;dij为所有的两点之间的欧式距离:
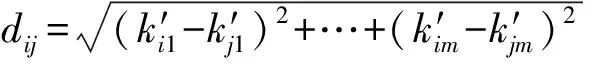
(12)
对于最高密度的点,习惯上选择:
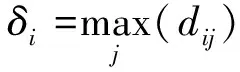
(13)
根据式(9)与式(11)得到每个点的ρi和δi,可以组成一个决策图,密度和距离同时较大的样本点,选择为聚类中心。基于确定的聚类中心,根据非聚类中心的点到聚类中心的距离可以实现非聚类中心点的分配,最终实现趋势特征的聚类。
根据前文所提到的,将变量的变化速率k作为数据段特征描述的因素,进行聚类分析。首先需要确定最优聚类数目,采用一种类内距损失函数的L型曲线确定拐点的方法进行最优聚类数的确定。类比于线性拟合误差的损失函数,可以表示出聚类后类内距的损失函数:
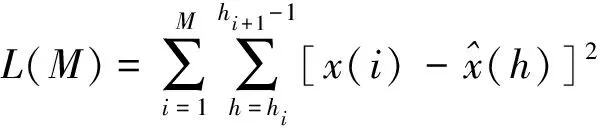
(14)
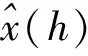
由于分类数目越多,类内距离越小,L(M)越小,但也同时会存在模糊类间特征(放大局部特征)的问题,因此最优的聚类数既要保证较小的类内距,又要保证类间的特征足够明显。损失函数L(M)的曲线呈现的是如图1所示的L型曲线变化。图1中的拐点在M*处取得,该点与相邻前后两点所连直线的夹角(拐角)应该是最小的,根据文献[21]中的方法,定义最优聚类数的决定函数公式如下:
F(M)=tanθ3=tan(θ1-θ2)=
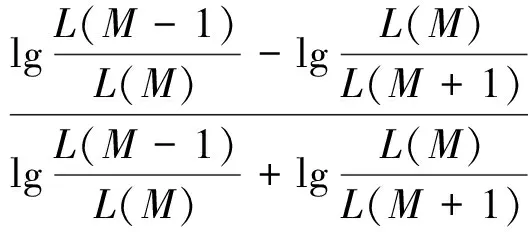
(15)
式(15)中:θ3为拐角的补角,由于拐角为类内损失函数曲线上可以取得的最小角,因此,θ3取最大值,即决定函数取最大时,所对应的聚类数为最优聚类数。最终,最优聚类数M*的计算公式如下:
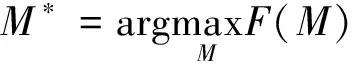
(16)

图1 L型曲线变化图Fig.1 L-shaped curve change chart
1.4 确定显著变化幅值的阈值
采用一种最新的基于拟合优度和噪声方差来确定显著变化幅值的阈值A0[22]:
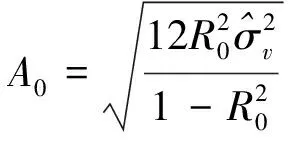
(17)
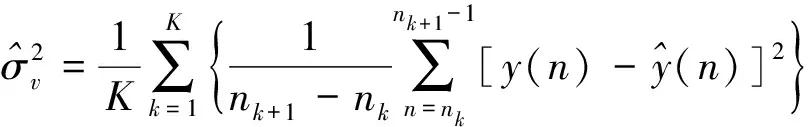
(18)
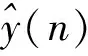
数据段的变化幅值a与阈值A0比较可以判断变量是否发生了显著变化:
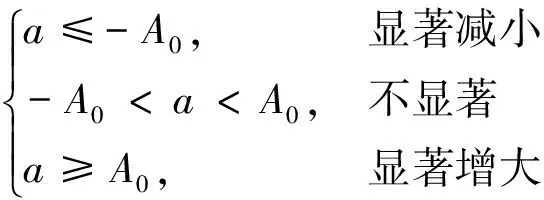
(19)
对于包含m个变量的趋势组合,每个变量求得的显著变化幅值的阈值为{A1,A2,…,Am},为了更有利于统计发生显著变化的变量,对所提取的变化幅值做标准化处理:
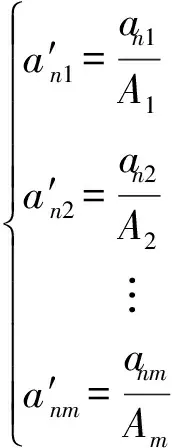
(20)
2 方法验证
为了论证本文所提方法的有效性,根据核心算法编写了MATLAB代码并通过仿真案例与工业案例对本文提出的多元相似时间序列提取的方法进行验证,通过与Matrix profile方法比较证明了本文所提方法的准确性和快速性。
2.1 仿真案例
本文构造包含三个变量的仿真数据,并分别用Matrix profile方法与趋势特征聚类方法进行历史相似时间序列的提取,对比两种方法说明本文所提方法的准确性和快速性。仿真数据构造过程如下。
构造第一个变量(主变量)的数据x=[x1,x2,…,xn],该变量含五组相似的时间序列以及随机噪声,时间长度为3 600 s,第二个变量和第三个变量的数据由y1=-0.5x(t)+5和y2=2x(t)+5生成。仿真数据如图2所示。

图2 仿真原始数据图Fig.2 Graph of simulation the orginal data
设定趋势提取段数范围1~20段,根据式(3)确定最优分段数为15段,采用1.2节的趋势提取方法对第一个变量进行趋势提取,在相同时间段内对第二个变量和第三个变量进行线性拟合,趋势提取结果如图3所示。

图3 仿真数据趋势提取结果图Fig.3 The plot of trend extraction results of simulation data
提取每段时间序列的斜率等趋势特征,根据变化幅值筛选发生显著变化的时间序列,并采用式(7)对趋势特征做标准化处理。
为了对趋势特征进行聚类,设定聚类数目的范围为1~8类,由式(14)和式(15)分别计算类内距的损失函数和决定函数,最终根据式(16)确定最优聚类数为5类。类内损失函数图如图4所示。
基于确定的最优聚类数,根据1.3节中介绍的DPCA聚类算法对发生显著变化的时间序列进行聚类,根据式(9)和式(11)计算ρi和δi,得到的决策图如图5所示。对ρi和δi标准化处理并计算决策图上的点到原点的距离,选择ρi或δi较大的点作为聚类中心。
根据非聚类中心的点到聚类中心的距离进行非聚类中心点的分配,实现聚类。每一类具有相似的趋势特征(斜率),最终找出五组相似的时间序列,如图6所示。
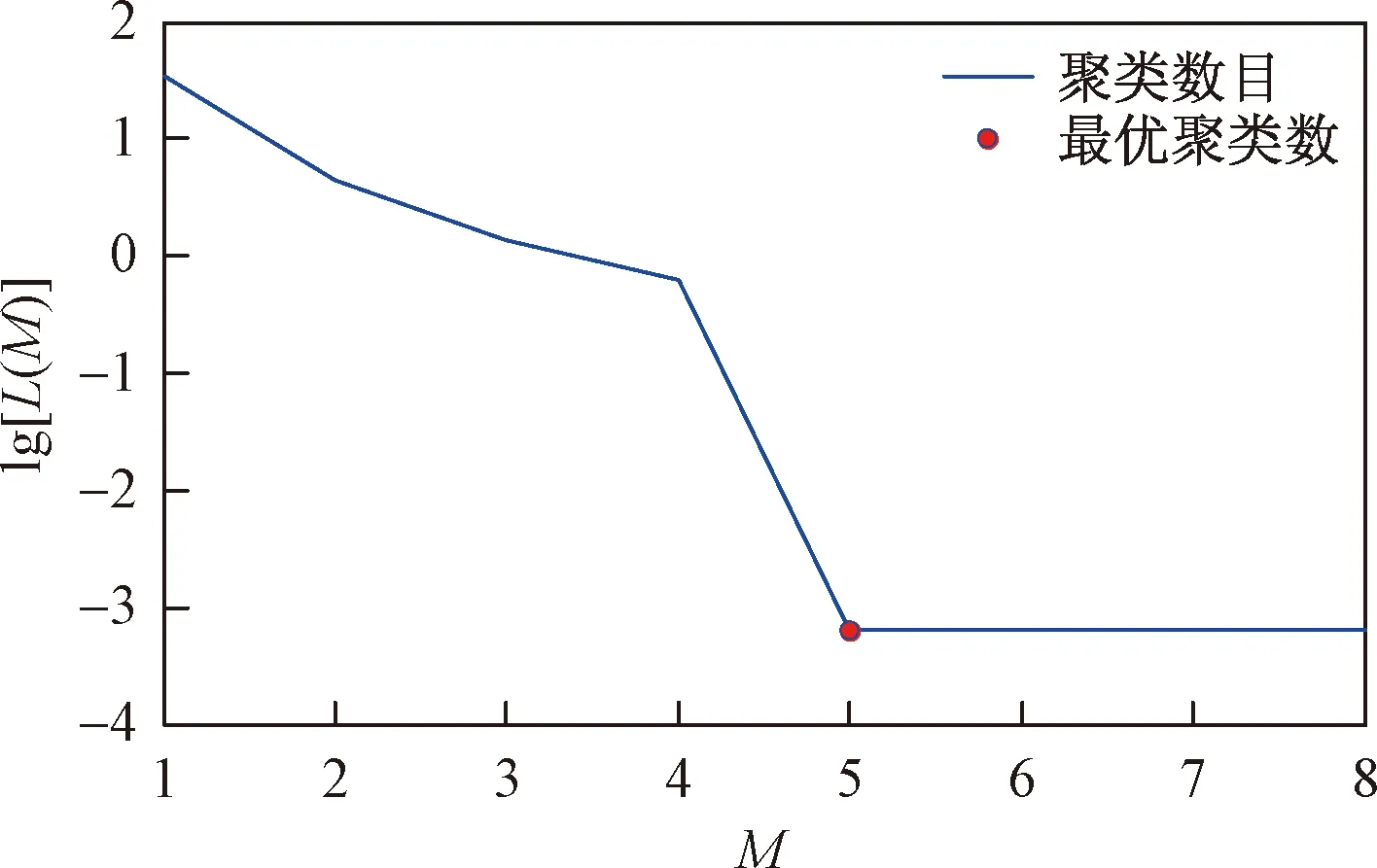
图4 仿真数据类内损失函数的曲线图Fig.4 The graph of intraclass loss function of simulation data
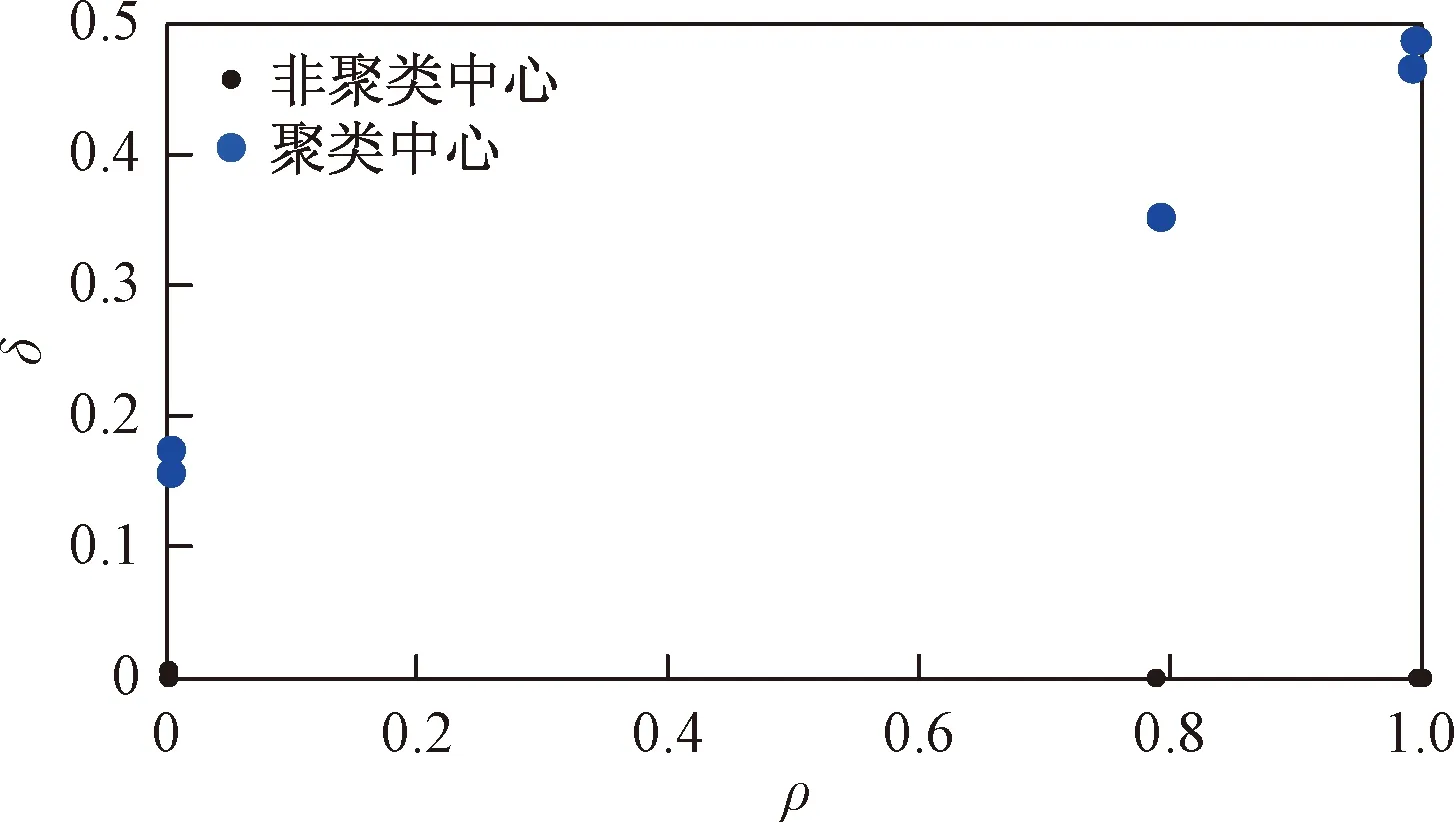
图5 聚类中心决策图Fig.5 The decision graph of cluster center
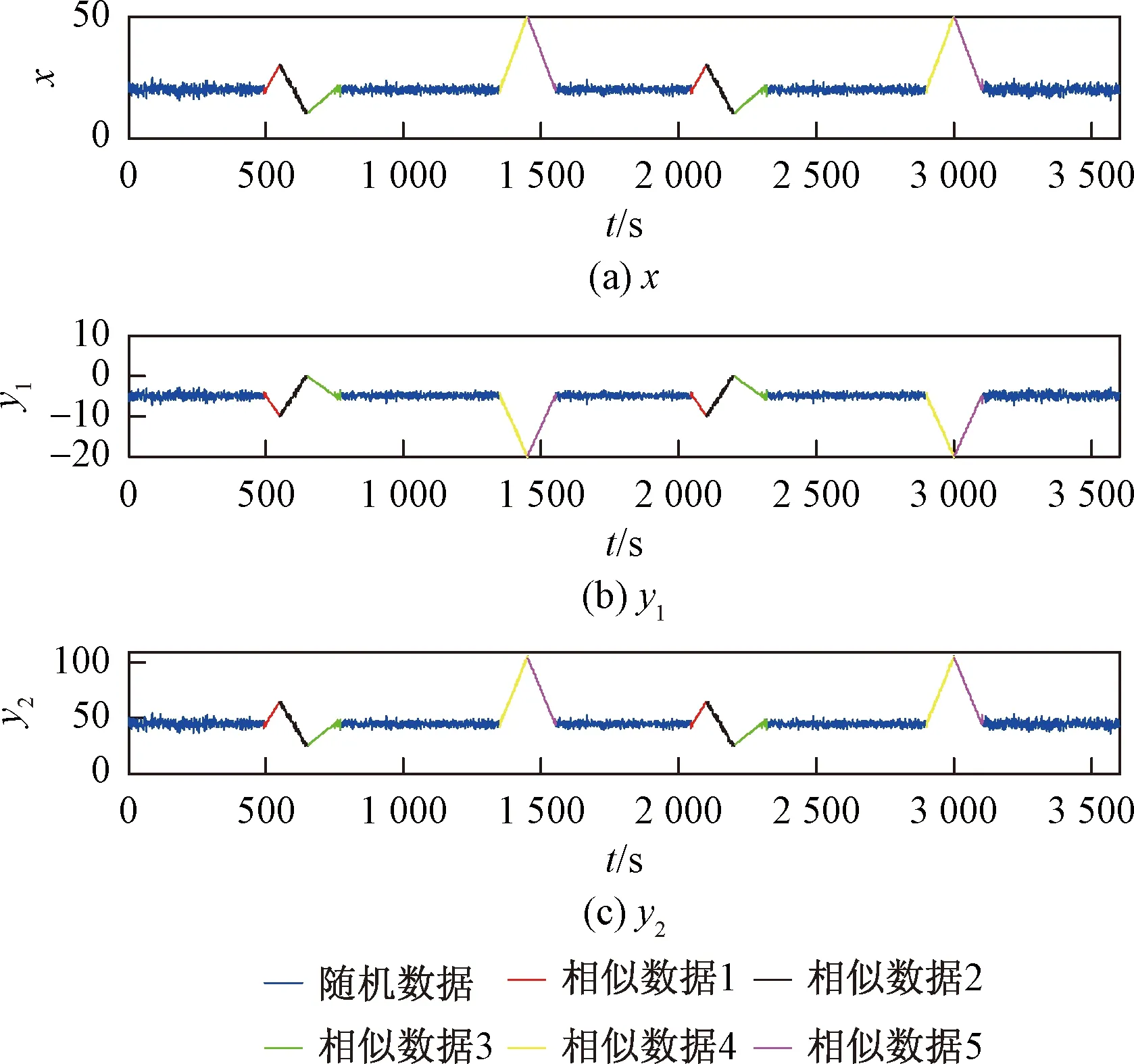
图6 本文所提方法的仿真结果Fig.6 Simulation results of the proposed method
为了证明本文所提方法的准确性和快速性,用同一仿真数据对Matrix profile方法进行仿真验证,Matrix profile是一个的数据挖掘工具,用于解决主题发现、形状发现以及异常检测等数据挖掘的问题[23]。假设时间序列的长度为n,用长度m的滑动窗口来提取长度m的所有子序列,每个子序列与其他子序列之间的最小距离组成Matrix profile。
设定窗口宽度为100,计算每一个时间子序列的最小距离得到Matrix profile,如图7所示。
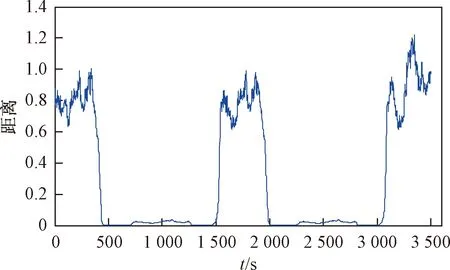
图7 Matrix profile方法的距离Fig.7 Distance map of the Matrix profile method
根据Matrix profile的计算结果最终实现对仿真数据多元相似时间序列的查找,查找结果如图8所示。
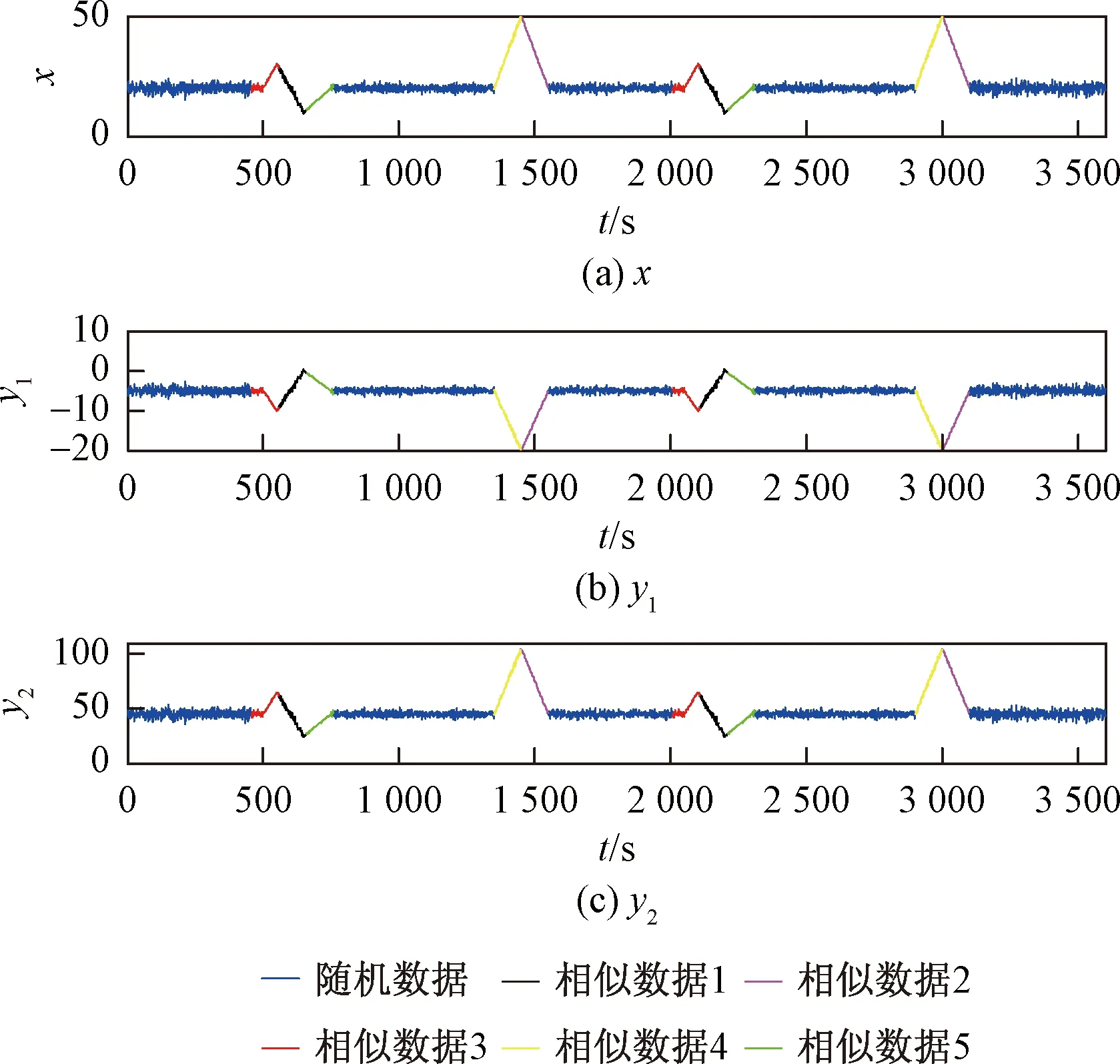
图8 Matrix profile方法的仿真结果Fig.8 Simulation results of the Matrix profile method
对比本文所提方法与Matrix profile方法查找多元相似时间序列的仿真结果。[500,550]与[2 050,2 100]为所设定一组相似的时间序列,本文所提方法找到的相似时间序列[495,550]与[2 044,2 100],由于Matrix profile方法受到窗口宽度的限制,查找的一组相似时间序列为[459,559]与[2 009,2 109],本文所提方法准确性更高。除此之外,Matrix profile方法运行了1 600 s,而本文所提方法只运行了14 s左右,运行速度明显优于Matrix profile方法。
2.2 工业案例
结合凝汽器系统的工艺知识,选取德州电厂#3机组2018年7月1—31日的4个变量的数据,并剔除不可用数据,包括:凝汽器真空、进汽温度、凝结水流量和冷却水入口温度。对上述四个变量进行历史相似数据段提取并进行凝汽器真空异常变化的根源分析工作。
对四个变量进行趋势提取,得到四个变量的斜率及幅值等趋势特征。部分趋势提取图9所示。
得到每个变量的斜率k,各个数据段表示为[k11,k12,k13,k14]的形式,筛选出凝汽器真空发生显著变化的数据段共452段,并对其做Z标准化处理。
聚类数目范围设定为5~50类,计算损失函数和决定函数,最终根据式(16)得到最优聚类数为33类,类内损失函数图如图10所示。

图9 凝汽器真空趋势提取结果图Fig.9 The plot of trend extraction results of condenser vacuum
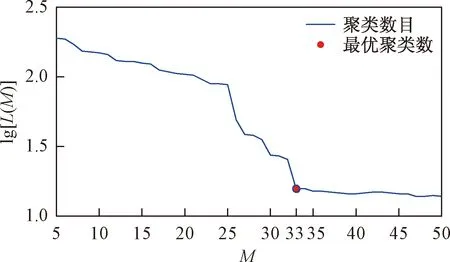
图10 工业数据类内损失函数的曲线图Fig.10 The graph of intraclass loss function of industrial data
基于确定的最优聚类数,得到的决策图,对ρi和δi标准化处理并计算决策图上的点到原点的距离,选择ρi或δi较大的点作为聚类中心。
根据非聚类中心的点到聚类中心的距离进行非聚类中心点的分配,最终实现聚类,聚类效果如图11所示。对数据段的趋势特征进行聚类后,具有相同趋势特征(斜率)的数据段被分到一类中,类间的趋势特征(斜率)差异明显。
根据式(17)和式(18)计算四个变量(凝汽器真空、进汽温度、凝结水流量和冷却水入口温度)幅值发生显著变化的阈值如表1所示。
统计凝汽器真空超过阈值的类别,并根据其变化幅值对统计结果从大到小排序,聚类后的统计结果如表1所示。
根据式(20)对各变量的变化幅值做标准化处理,可以通过比较标准化后的变化幅值的绝对值与1的大小来判断发生显著变化的变量,标准化后的数据趋势特征的聚类结果如表1所示。
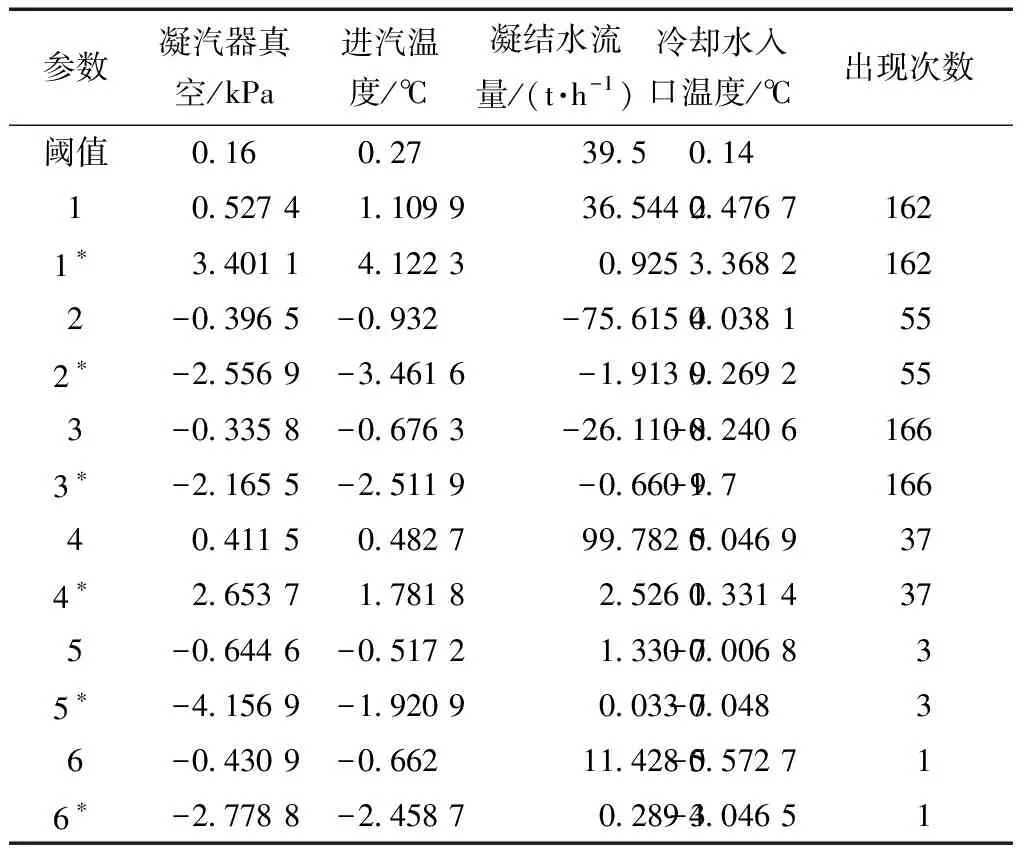
表1 标准化前后的数据趋势特征的聚类结果展示
注:*表示该行数据为标准化后的聚类结果。
观察表1可知,标红的变量超出显著变化的阈值并且在3个关联变量中变化幅值最显著,因此,可以认为凝汽器真空异常变化的根源是由该变量导致的。如图11展示的相似数据段中,标黄的部分表示凝汽器真空发生显著变化的根源变量,分别为凝结水流量和进汽温度。
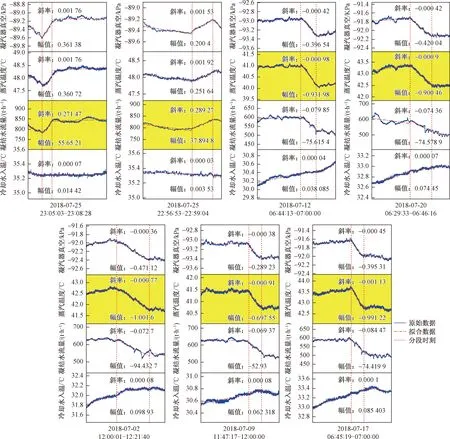
红色虚线间的数据段为聚类后相似的数据段图11 相似趋势组合的聚类结果Fig.11 Clustering result of similar trend combination
3 结论
提出了一种基于趋势特征聚类的多元相似时间序列的提取方法,可以有效地辅助现场工作人员分析关键变量发生异常变化的根源,得到以下结论。
(1) 对多元时间序列进行分段线性表示,并采用一种有效的方法确定最优分段数,从而获得更加准确的趋势特征信息。
(2) 改进确定最优聚类数的方法,提高了时间序列趋势特征在高维空间进行DPCA聚类的准确性,从而实现历史时间序列的相似性查找。
(3) 采用一种新的判断时间序列发生显著变化的方法分析导致主变量发生异常变化的根源变量。
基于对历史时间序列的相似性提取,后续可以通过该方法进行工业过程中的在线报警根源分析工作,当类似的故障再次出现时,可以根据历史中的相似时间序列快速找到当前发生报警故障的根源,对提高工业生产效率和减少工业现场的安全隐患具有很大的意义。
