基于系统因素分析法和优劣解距离法的全寿命周期故障排序

罗 静, 李 豪

(重庆理工大学机械工程学院,重庆 400054)

近年来，故障模式、影响度及危害性分析(FMECA)技术发展迅速。FMECA中的风险优先数法(RPN)在数控机床的可靠性应用上很多，但是数控机床是一个复杂的机电产品，故障模式及故障原因之间的关系特别复杂[1-2]。数控机床经常受到这些复杂关系的影响，从而在应用传统RPN法进行故障排序时，会存在以下问题：①仅考虑故障模式或故障原因本身的严重程度，没有考虑在全寿命周期各个阶段间的危害度相互之间的影响，忽略了有些影响因素具有传递的特性；②RPN法是依据故障模式中几个因素的乘积大小进行故障排序，其数值的选取比较片面单一，数值间隔太大等。

为了解决以上存在的问题，结合实际数控机床的故障情况，提出以下方法：①考虑故障之间的影响关系[3-4]，应用DEMATEL权重-TOPSIS方法进行排序，以设计FMECA的RPN计算值与过程FMECA的RPN计算值的关系作为DEMATEL(决策实验室分析法)的输入;②为克服求规范决策矩阵的复杂性，使得排序数值差异化明显，且为了比传统的TOPSIS方法更具有操作性，避免传统RPN法排序的单一性，将加权距离平方和作为改进TOPSIS方法(逼近于理想解的排序法)的核心计算过程。

根据项目合作企业的故障数据记录和相关设计人员的反馈情况，对数控机床中的伺服驱动系统进行分析。在文献[5]中10例故障模式的基础上，取伺服驱动系统的主要故障模式为分析样本，最后将得到的排序结果与传统的危害度排序结果进行比较和讨论，合理地得到伺服驱动系统的薄弱部件。

1 排序理论分析

传统数控机床失效模式的危害度是根据RPN计算值来进行表示，RPN计算值越大其危害性越大，排序结果靠前。但是RPN法的取值受到分析人员的主观因素影响，容易有误差产生，而这些误差在RPN法的运算中很容易被放大，造成RPN法排序的混乱，因此一些关键的故障模式容易被忽略[6]。

根据实际情况，针对在不同的应用场景和不同的全寿命周期阶段，会有不同类型的FMECA。根据型号可靠性手册[7]中的FMECA分类方法，其中功能FMECA、硬件FMECA、软件FMECA、DMEA属于设计FMECA。因此FMECA主要是两个大类型：设计FMECA和过程FMECA，而这两个类型的FMECA涵盖了产品寿命周期各个阶段，见图1。

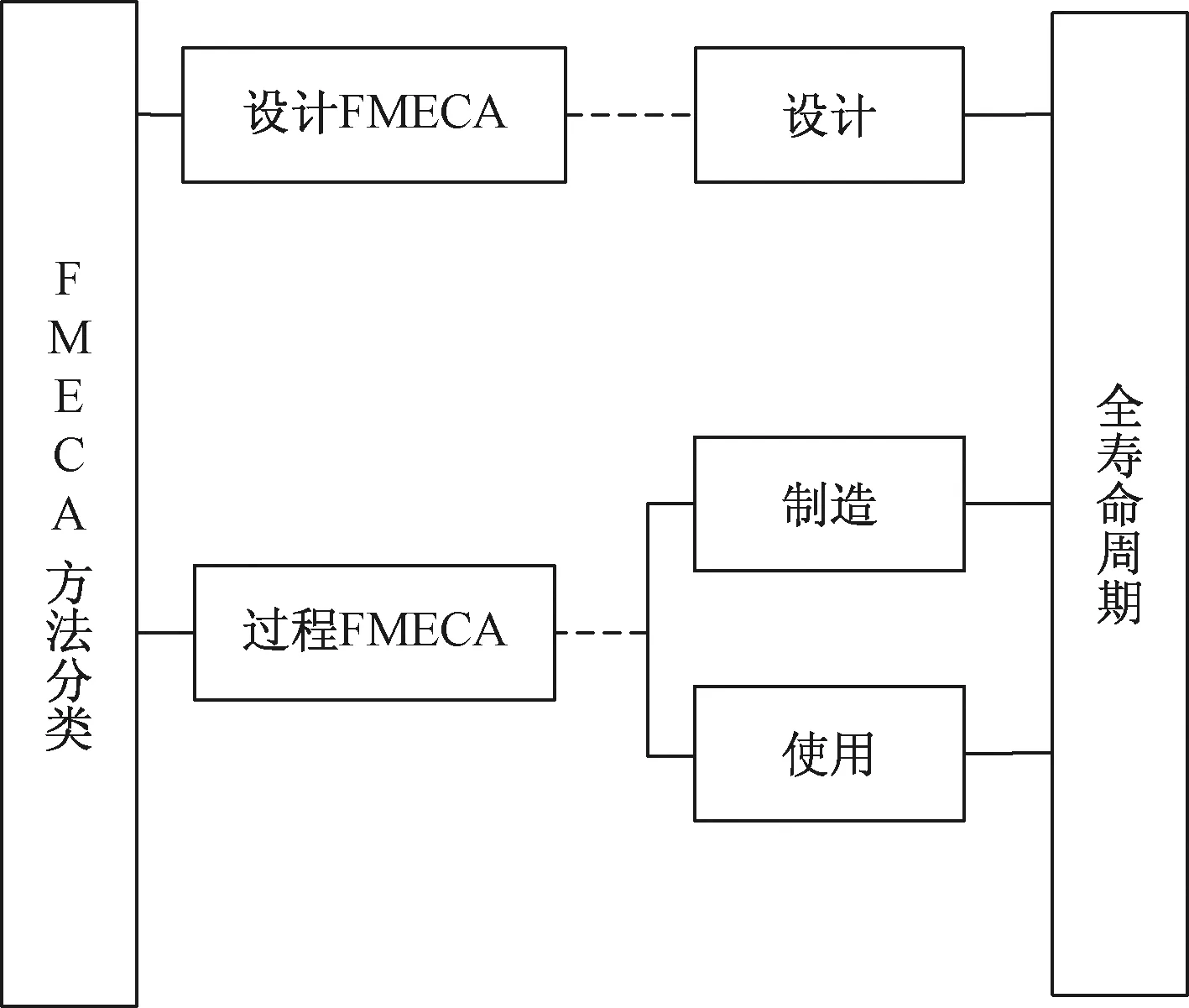
图1 FMECA与全寿命周期图Fig.1 FMECA and life cycle diagram

不同类型的FMECA会产生不同的RPN计算值，为了保证故障模式评级的客观性，挖掘出输入数据隐含的全寿命周期特点[8]。通过SPSS软件分析出设计FMECA的RPN计算值与过程FMECA的RPN计算值的关系值，将这个关系值作为DEMATEL权重-TOPSIS法的输入值。DEMATEL是一种有效确定相互影响程度的方法，但是对于较为复杂的系统却不好分析，为了完善DEMATEL方法，引入TOPSIS方法，见图2。

图2 排序理论图Fig.2 Scheduling theory diagram

2 传统RPN法排序

数控机床中的伺服驱动系统是关键薄弱子系统，经常产生较多的故障模式。在设计FMECA中，应用RPN方法排序：

RPN=OPR×ESR

(1)

式(1)中：OPR是该故障模式发生概率等级；ESR是该故障模式影响的严酷等级。

根据文献[7]的评分准则对伺服驱动系统主要的故障模式进行危害性分析，结果见表1。

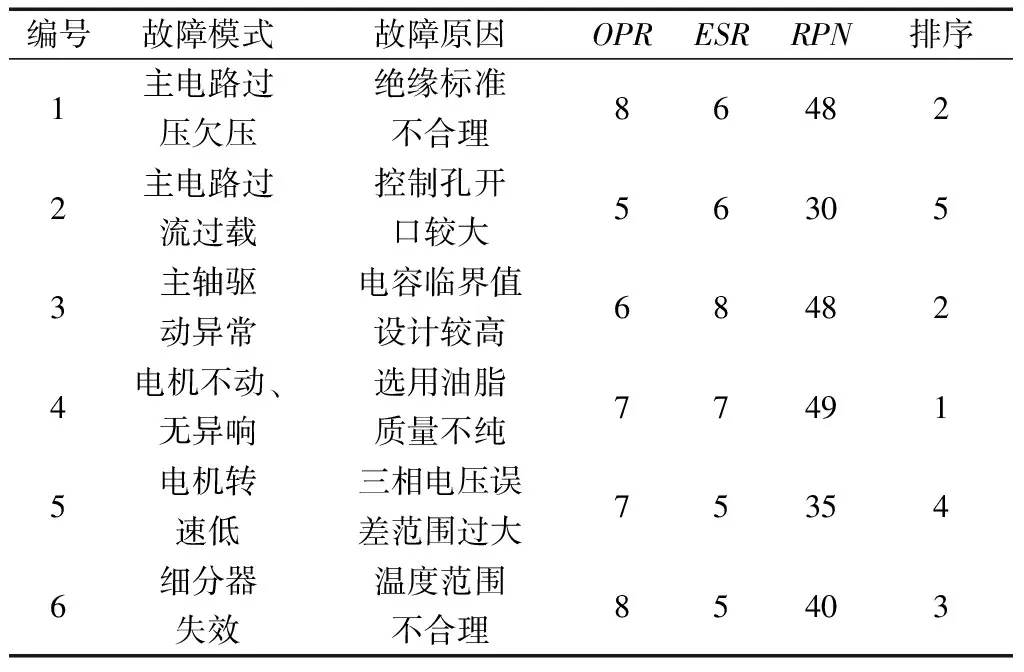
表1 故障模式设计(D)RPNTable 1 Failure mode design (D) RPN

通过计算表明:R4>R1=R3>R6>R5>R2。电机不动、无异响排序第一，同时排序第二的有2个故障模式，分别是主电路过压欠压和主轴驱动异常。传统的RPN排序出现2个问题：①排序第一和第二的故障模式的RPN计算值相差不大，如果这样定下排序顺序，难免有些欠妥;②排序第二的故障模式是并列的，两个值一样，虽然RPN计算值相同，但是隐含的风险是不相同的。

3 DEMATEL权重-TOPSIS法排序

3.1 过程FMECA的RPN法

在第2节中，根据设计FMECA中的RPN计算值已经排出了主要的6个故障模式等级。此排序方法只考虑了全寿命周期设计阶段，为了全面分析故障数据，加入过程FMECA的RPN法。通过对全寿命周期故障数据的分析发现：即使是相同的故障模式在不同的寿命周期场景下会因为不同的故障原因而产生[9-10]，因此同样的故障模式会现在过程FMECA中，见表2。在过程FMECA中，应用RPN方法：

RPN=SOD

(2)

式(2)中：S是故障模式严酷度；O是故障模式发生概率；D是故障模式探测度。

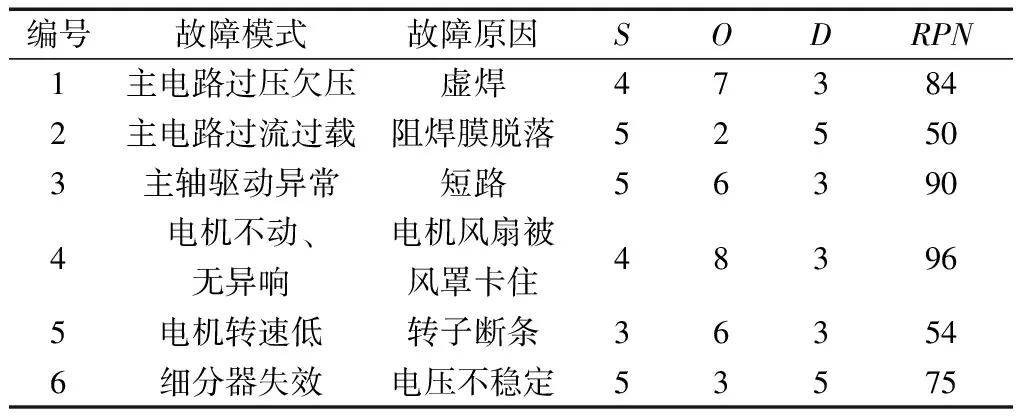
表2 故障模式过程(P)RPNTable 2 Failure mode processes (P) RPN

3.2 计算过程与分析

第2节和3.1节由于只引用了一位专家的评分数据，难免不太客观和准确。因此，选取12位专家来进行评分，制定故障模式评分表[11]，在故障发生和处理时进行填写，见表3。

表3 RPN评分计算Table 3 RPN score calculation

RPN计算值的基础数据由专家评分而来，会存在一定的偏差，可以观察发现存在以下现象：①在设计FMECA的RPN计算值中专家B和专家L的评分相差44，在过程FMECA的RPN计算值中专家B和专家L相差106，专家对RPN法中的因素评分相差1就会造成RPN计算值差值明显；②RPN法的取值不是连续数字，S、O、D的取值是在1～10，经过式(1)、式(2)计算的值并不能取到1～1 000之内的数，有些数字会丢失，能取到的数值只占12%左右，像11、13、17是不能取到的。这两个现象是客观存在的，同时也是RPN法存在的数学缺陷[6]，如何保留RPN法的数值意义，同时又克服RPN法存在的问题。通过对数据进行分析，可以发现RPN法因素的取值浮动不会太大，因为专家对一个因素的取值都差不多，有相差存在，但是不会太偏离。比如其中一个因素取7，不可能有专家取2，只会在7上下浮动，如8或者9。如果存在相差值较大，这种评分值会被认为无效。根据这种评分数据特征，检验是否存在相关性，应用SPSS软件对数据进行相关性检验，结果见表4，可以发现双尾值接近0小于0.05，说明显著相关。将其绘制成散点图，并进行拟合，见图3。再进行R方检验，R方值为0.885，符合线性回归。

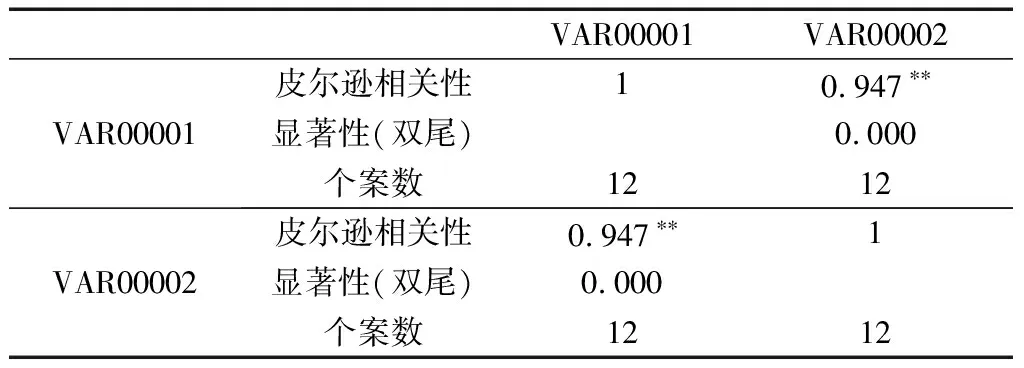
表4 相关性检验Table 4 Relevance test

注：**. 在 0.01 级别(双尾)，相关性显著。

以故障模式1为算例表明，两者关系有2.190 9倍数的关系。

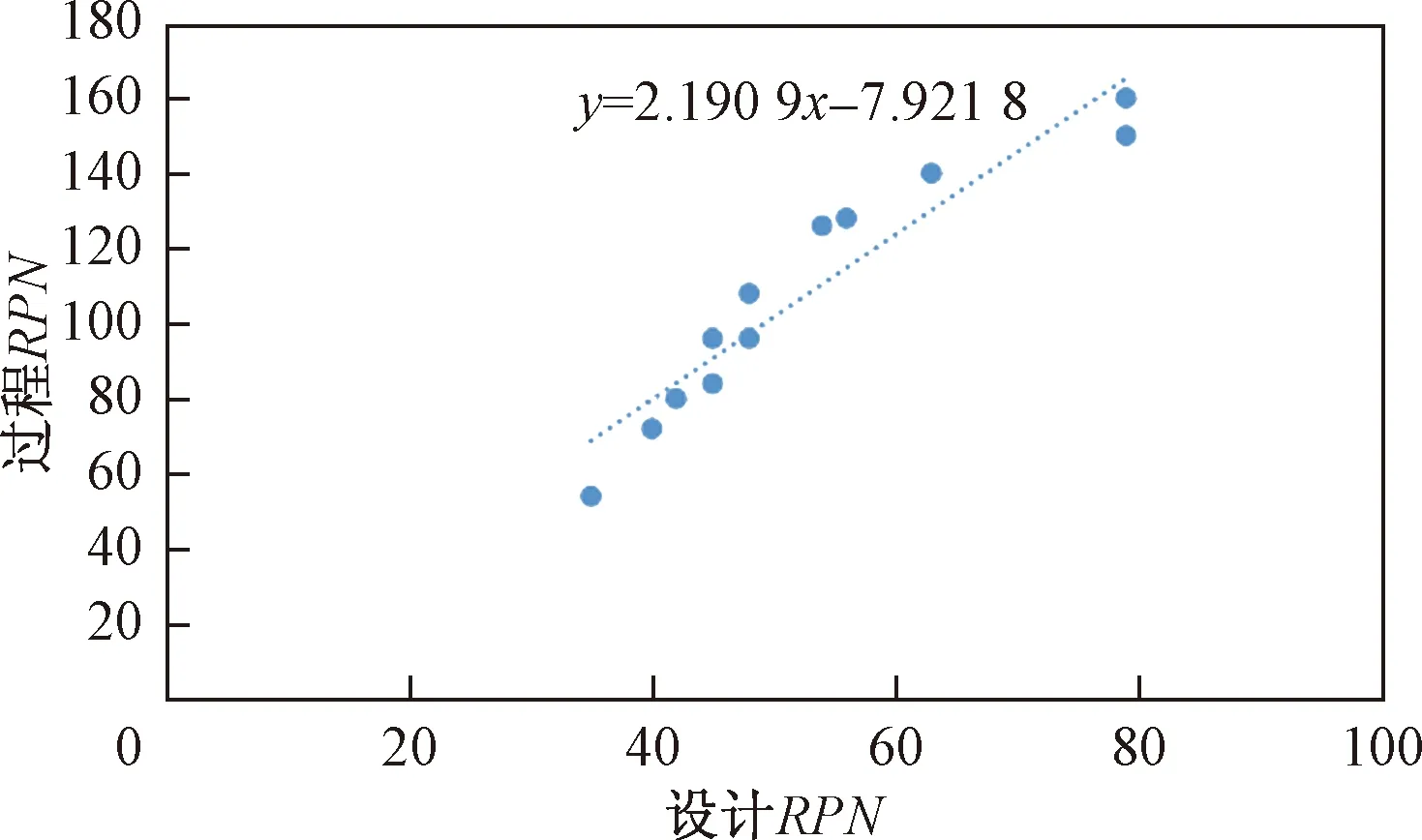
图3 RPN关系图Fig.3 RPN diagram

同理，因为是同样的评分特性和范围浮动，对这主要的6种故障模式的RPN进行分析，可以得到各个故障模式RPN计算值之间的关系，得到结果见表5。

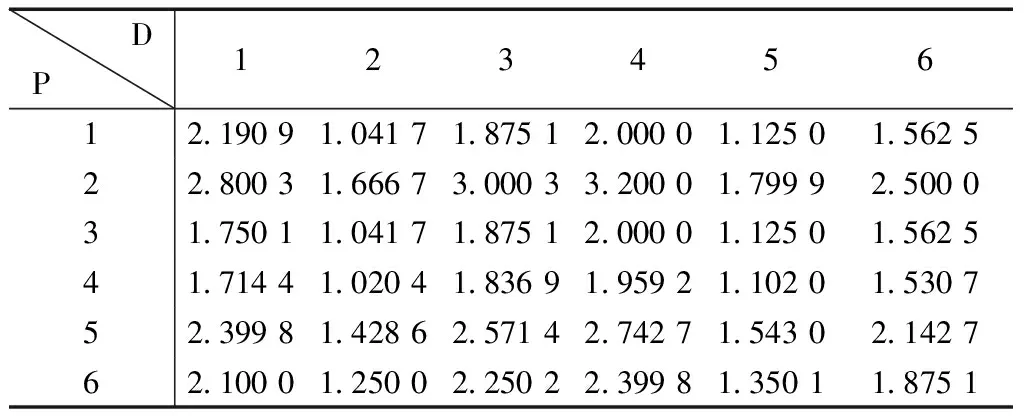
表5 过程(P)RPN与设计(D)RPN的关系值Table 5 Relational value of process RPN and design RPN

计算出的相关系数值满足以下论述：①克服了同种类型的RPN计算值相差较大的缺点，同时关系值保留了6个故障模式评分的客观性;②根据文献[1]中的DEMATEL输入分析，文献采用的是设计FMECA中的危害性矩阵分析方法，此方法只考虑了设计过程，因此有一定的不足。为了保持整个分析过程的一致性，加入了过程FMECA的危险优先数法;③考虑到全寿命周期故障之间关联性，以设计RPN法计算值和过程RPN法计算值的关系值作为DEMATEL输入正好体现故障发生在全寿期的整个过程以及故障之间的相互影响关系。

因为设计阶段在过程阶段之前，因此输入数据为：aij=设计RPN法计算值/过程RPN法计算值(D/P)。对表5中的数值求倒数，构建直接影响矩阵A=[aij]n×n，见表6。

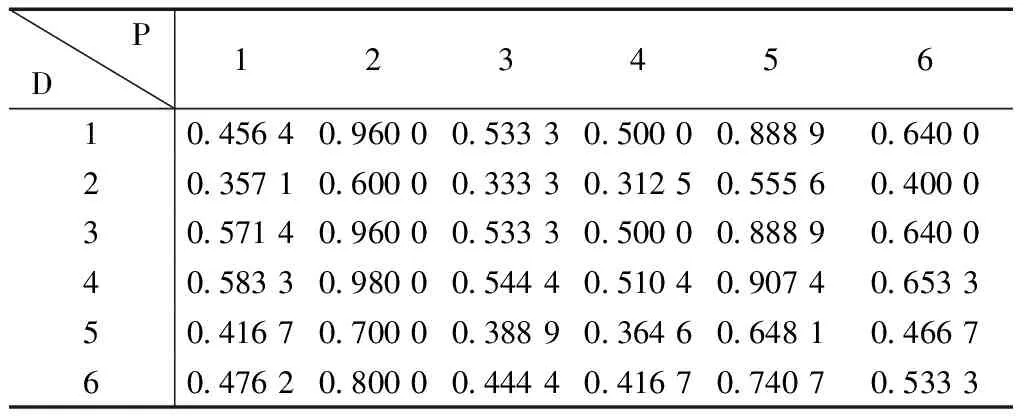
表6 DEMATEL直接影响矩阵ATable 6 DEMATEL directly affects matrix A

求得的直接影响矩阵A对其标准化处理，其计算公式为

(3)

从而得到标准化直接影响矩阵N，见表7。

求得的标准化直接影响矩阵N对其综合运算，其计算公式为

(4)

式(4)中：I为单位矩阵，从而得到综合矩阵T，见表8。

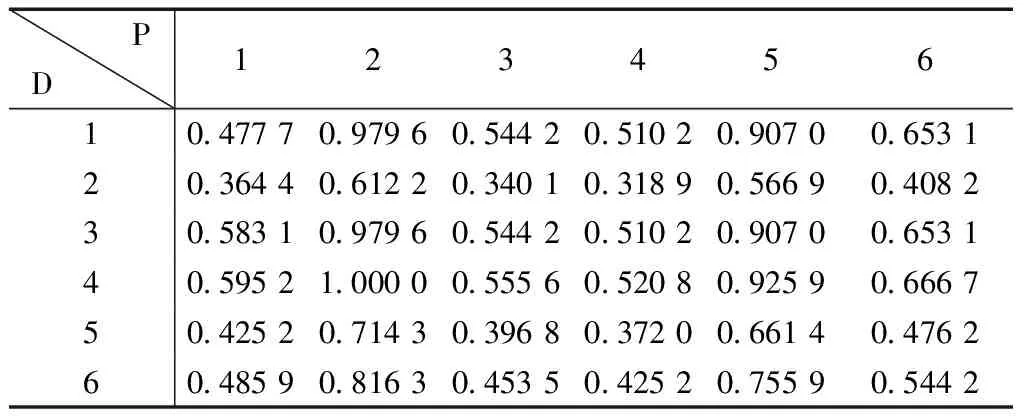
表7 DEMATEL标准化直接矩阵影响矩阵NTable 7 DEMATEL standardized direct matrix impact matrix N

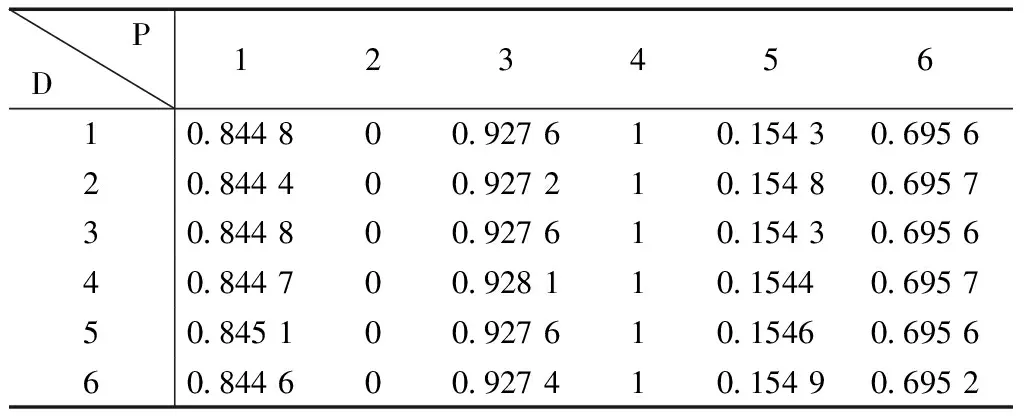
表8 DEMATEL综合矩阵TTable 8 DEMATEL synthesis matrix T

根据综合矩阵，求得影响度fi、被影响度ei、中心度ri、在求得中心度ri后可求得权重wj，见表9。其计算公式分别为

(5)

(6)

ri=fi+ei

(7)

(8)

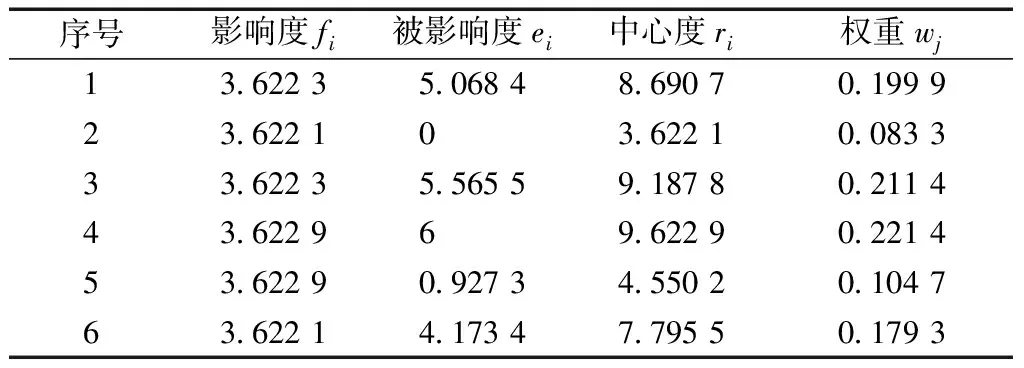
表9 DEMATEL分析结果Table 9 DEMATEL analysis results

根据DEMATEL分析结果表明，故障模式的权重矩阵为W=[0.199 9 0.083 3 0.214 4 0.221 4 0.104 7 0.179 3]。

TOPSIS是通过对计算目标是否存在最优解和最劣解的距离来进行排序，如果计算目标最接近最优解和最远离最劣解，则这个值为最好；反之最差。TOPSIS需要输入权重，传统TOPSIS方法中的权重是事先确定的，主观性比较强，因而具有一定的随意性[12]。运用DEMATEL计算，可以客观地得到权重值w。将表8 DEMATEL综合矩阵T作为TOPSIS标准化矩阵R(rij)。TOPSIS算法有5个步骤，其核心计算是与理想距离的值。为了便于运算DEMATEL权重-TOPSIS法，避免烦琐的计算步骤，同时体现TOPSIS算法的核心算法，在文献[12-13]的分析基础上，直接以式(9)、式(10)进行计算。则TOPSIS加权距离平方值gi为

fi(w)=fi(w1,w2,…,wn)=

(9)

(10)

将R(rij)中各数据代入式(9)、式(10)中得gi=[10.53 100 0 52.63 73.68 15.79]。

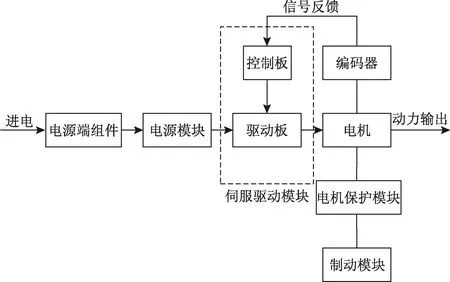
由故障模式加权距离平方值知，f3

4 排序结果的对比和讨论

针对这主要的故障数据，将DEMATEL权重-TOPSIS法的排序结果和直接由设计FMECA得到的传统RPN法排序结果进行对比分析，见表10。

表10 RPN和DEMATEL权重-TOPSIS法排序对比Table 10 RPN and DEMATEL weight-TOPSIS sort comparison

通过对表10的排序结果可得出如下结论。

(1)传统的RPN法存在的问题在DEMATEL权重-TOPSIS法排序中得到了解决。在传统的RPN法排序第一和排序第二相差不大的情况下，在DEMATEL权重-TOPSIS法中避免了这种情况： DEMATEL权重-TOPSIS法计算很精确，6个gi排序值差异化明显，能够清楚地得出排序结果。

(2)传统的RPN法排序存在2个排序值相同，但是在DEMATEL权重-TOPSIS法中能明显地区分这种情况，不存在排序相同的问题，挖掘出了RPN计算值相同，风险却不同的弊端。

(3)在传统RPN法排序中，主轴驱动异常排序第二，但是在 DEMATEL权重-TOPSIS法排序第一，这是因为电机不动、无异响属于失调性故障，维修时间较短，对生产人员和工作环境影响不大，在DEMATEL权重-TOPSIS法排到了第四；而主轴驱动异常维修烦琐，主轴驱动的异常会影响到切削力，严重影响生产工件的质量，造成工件不合格，而且这种故障发生不容易检测，维修时间较长，因此主轴驱动异常故障模式排序高于电机不动、无异响。同时经过跟现场技术人员的确认，DEMATEL权重-TOPSIS法排序符合实际和经验认可。

(4)通过对主轴系统的模块分析和现场维修师傅的经验认知：可以排除主轴硬件结构问题，因为主轴硬件结构一般质量较高，很少出现硬件结构性问题。然后对伺服系统运行图分析见图4，从而确定造成主轴驱动异常的部位是驱动模块中的驱动板。因此，数控机床使用者应该采取相关措施来降低故障率，例如，定期检查驱动板，驱动板也称为逆变器，电流电压经常受温度的影响，应该做好降温处理。如果驱动板是外购件，可以选用质量较好的品牌。只有这样才能改善伺服系统的可靠性和质量。

图4 伺服系统运行图Fig.4 Servo system working diagram

5 结论

基于DEMATEL权重-TOPSIS法提出了一种新的故障排序方法：首先通过已知的RPN法的关系值作为输入DEMATEL中，然后计算TOPSIS需要的权重值，最后把权重值输入到TOPSIS的距离公式中。此计算方法弥补了其他分析方法仅进行单因素和相关性分析的不足；采用的数据具有全寿命特点，克服传统数据的单时间特性；TOPSIS权重值不受专家确定的主观影响；应用该方法对伺服系统主要的故障进行排序，得出主轴驱动异常具有最高的优先顺序；同时该计算方法也可以应用到其他设备故障评级，此DEMATEL权重-TOPSIS法所得故障风险的优先级排序更为客观，该方法具有一定的实用性和操作性。研究引用的故障模式是主要的、出现在全寿命周期中的故障模式，而对非主要故障模式没有进行探讨，这将是下一步研究的内容。