基于Hilbert-Huang变换的离心泵故障诊断

胡泽，王晓杰，张智博，吴雨宸

( 西南石油大学 电气信息学院，四川 成都 610500 )

0 引言

离心泵设备广泛应用在石化、电力、机械以及军工部门的关键设备。因此，离心泵故障诊断的研究技术是非常重要的[1]。目前，利用振动信号进行故障诊断是应用最广泛的方法[2]。故障诊断一般分为三个步骤：首先是振动信号的采集；然后是提取振动信号的特征；最后是模式识别和故障诊断。其中最关键的是提取振动信号的特征。离心泵的结构复杂，激振源较多，且相互干扰，因此离心泵的振动信号是一种非线性、非平稳信号[3]。HHT具有较强的自适应性，能直接反应出信号的时频本质，对非线性、非平稳信号具有很大的优势。Hilbert-Huang变换主要包含经验模态分解(Empirical mode decomposition，EMD)和希尔伯特变化(Hilbert transform，HT)两部分[4-6]。对一个复杂的信号采用EMD分解，得到若干个固有模态函数(Intrinsic Mode Functions，IMF)，在用HT对每一个IMF分量进行解调，得到由瞬时频率，瞬时幅值和时间组成的希尔伯特谱，包含了原始信号所有的时频信息。

本文利用HHT对离心泵的振动信号提取特征，输入到RBF(径向基)神经网络进行模式识别和故障诊断，可以使神经网络更好地进行学习，提高诊断率。

1 原理及特征

1.1 HHT原理

HHT假设任意一个信号都有若干个IMF构成[4-6]，其中IMF应当满足以下面条件：

1）数据中的极值个数理论上必须与零点的个数相等或最多相差1个；

2）对于任意的一个点，由局部极小值确定的信号包络和局部极大值确定的信号包络的平均值为零。

HHT中描述信号的基本量为瞬时频率(Instantaneous Frequenc，IF)，由于经过EMD分解之后的IMF都是瞬时频率有意义的、幅度或频率受调制由高频到低频的时间序列，而IF通过IMF的HT获得信号的解析形式z(t)为：

其中振幅函数ai(t)为：

相位函数θi(t)为：

对相位函数求导得到瞬时频率fi(t)为：

1.2 特征提取算法

为获取离心泵振动信号的特征向量，做了以下的定义：

平均瞬时频率Fi为：

经过EMD分解后，各层IMF的平均能量Ei为：

各层的总平均能量E为：

其中：N—每层IMF的数据点数；

各层IMF的能量占比Mi为：

2 设备情况

2.1 离心泵组

本文选用的设备为嘉利特荏原泵业有限公司的一款离心泵。工作基本参数为：主机型号200×150（A）DCS5M；运输介质为贫胺液；额定流量为200m3/h；额定扬程为150m；额定转速为2900r/min；额定功率为1120kW/h。数据采集中，采样频率设置为800Hz，采样点数为1024点。离心泵结构图和传感器测点位置如图1，测点布置情况见表1。

表1 测点布置情况

采集正常、转子不对中、转子不平衡、基础松动和油膜涡动及振荡共5种情况的振动位移信号，每种情况各40组，共200组振动位移信号。

3 特征提取

由于有6个传感器采集到的信号，而且不同情况所对应的振动方向不同，为了突出对比离心泵的振动信号，现抽取离心泵在4种故障发生时故障端且该故障的主要振动方向上所对应的传感器振动位移信号。正常情况下，抽取驱动端轴向传感器，即3号传感器的振动位移信号。对以上提及到的信号数据进行HHT变换处理。

以正常状态和油膜涡动故障为例，对一组振动位移信号做HHT变换，结果如图2和图3所示。

表2为正常状态振动位移信号IMF的平均瞬时频率和能量占比和各层IMF与原函数之间的相关系数。从表2和图2可以看出，IMF4-IMF7包括余量与原函数相关系数很低，而且能量占比也很低，不能代表离心泵正常状态时的振动信号特征。由离心泵正常状态时的平均瞬时频率和hilbert谱可以看出IMF2对应的51．52Hz，在1倍频附近，同时IMF2的能量占比最大，与原函数之间的相关系数最高，表明当离心泵处于正常状态时，1倍频起到主要作用。这符合离心泵正常运行时的典型振动信号[7]。

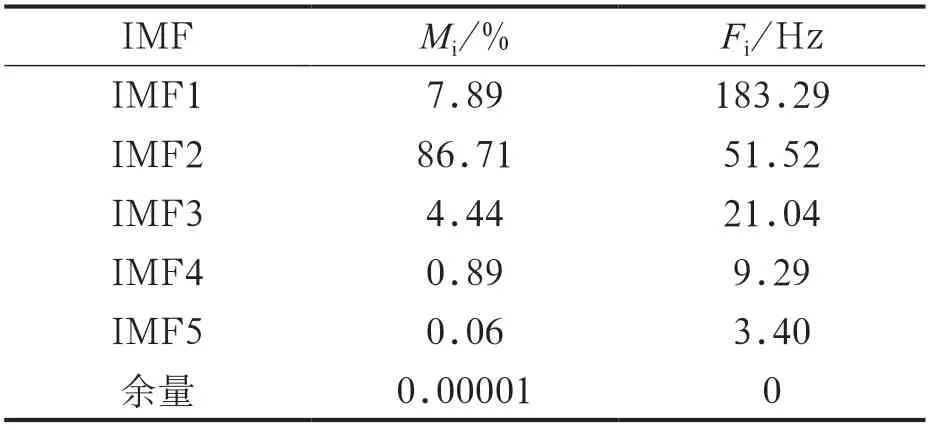
表2 正常状态振动位移信号IMF的平均瞬时频率(Fi)和能量占比(Mi)

表3为油膜涡动状态振动位移信号IMF的平均瞬时频率和能量占比和各层IMF与原函数之间的相关系数。从表3和图3可以看出，由于IMF4-IMF7包括余量与原函数相关系数很低，而且能量占比也很低，不能代表离心泵油膜振荡状态时的振动信号特征。由离心泵油膜振荡状态时的平均瞬时频率和hilbert谱可以看出IMF2对应的49．18Hz，在1倍频附近，同时IMF2的能量占比为51．43%，与原函数之间的相关系数为69．00%；IMF3对应的24．17Hz，在0．42～0．48倍频附近，同时IMF3的能量占比为46．45%，与原函数之间的相关系数为65．83%，表明当离心泵处于油膜振荡时，信号的能量主要在1倍频和0．42～0．48倍频处，这符合典型的半速涡动振动信号。这时，离心泵运行状态为油膜振荡的典型振动信号[7]。

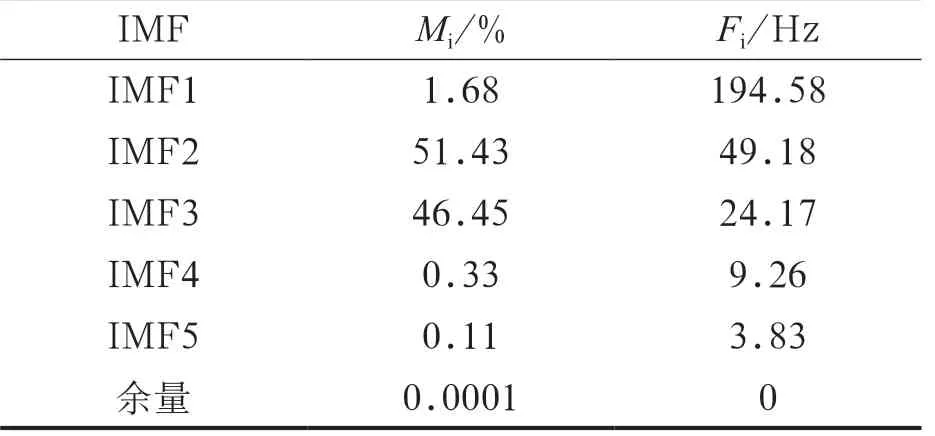
表3 油膜涡动状态振动位移信号IMF的平均瞬时频率(Fi)和能量占比(Mi)

利用同样的方法，对离心泵的不对中，不平衡，基础松动状态下的振动位移信号进行处理，通过大量数据处理的结果如见表4和表5。

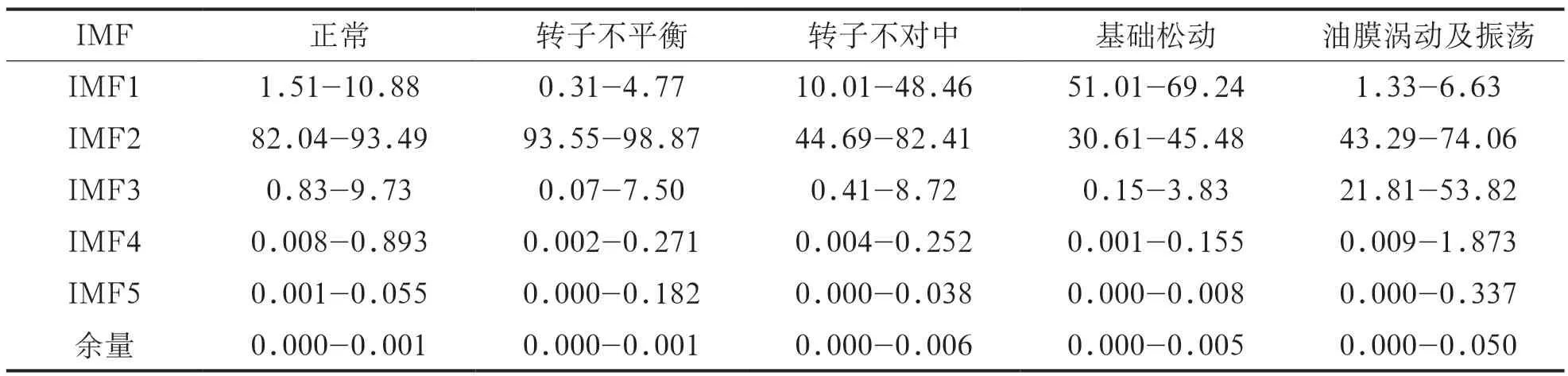
表4 离心泵各状态振动位移信号的IMF所对应的能量占比(Mi)(%)

如表4所示，离心泵的振动信号经过HHT处理过后，绝大多数能量都在前三层，即IMF1-IMF3中，不同故障状态对应IMF层的能量占比也各不相同。IMF4-IMF7包括余量的能量占比很低，不能代表离心泵运行状态时的振动信号特征。

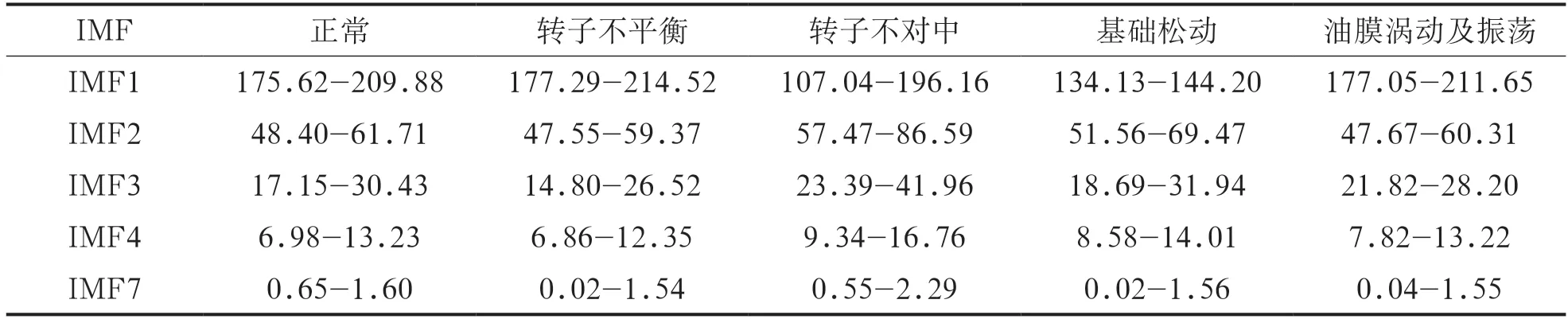
表5 离心泵各状态振动位移信号的IMF所对应的平均瞬时频率Fi（Hz）

如表5所示，离心泵的振动信号经过HHT处理过后，各层IMF的平均瞬时频率主要区分在于前3层，即IMF1～IMF3，而后续4层的平均瞬时频率没有特别明显的区分度，所以离心泵的振动信号经过HHT处理后，各个状态的前3层IMF分别对应的能量分布和平均瞬时频率分布是不同的，表明两者与离心泵当前所处的状态相关。

对离心泵的振动信号进行HHT处理，首先求出前3层IMF各自的平均瞬时频率并进行归一化处理，构成3维平均瞬时频率分布向量。然后求出前3层IMF各自的能量占比，构成3维能量分布向量；将能量分布向量和平均瞬时频率分布向量结合构成6维的能－频分布特征向量。由于是选择6个传感器同时输入离心泵的振动信号，所以构成一个36维的能量和频率分布特征向量。

4 识别结果

RBF神经网络在逼近能力、学习速度和分类能力等方面都由于BP神经网络[8-10]。因此，本文选用RBF神经网络作为离心泵振动位移信号故障诊断的工具。首先选取5种状态各30组特征向量作为训练样本，输入到RBF神经网络进行训练，对应的状态作为理想输出，网络训练误差曲线如图4所示。

训练完成后，从训练样本意外的数据中抽取10组特征向量进行检测网络。测试结果如表6所示。

表6 RBF神经网络诊断结果

5 结语

HHT对处理离心泵的振动信号具有很好的效果，经过EMD分解后得的IMF代表着离心泵振动信号各种信息。通过对各层IMF进行分析，提取出离心泵各状态振动信号的能 -频分布特征向量，该特征向量同离心泵所处状态紧密相关，因此用该特征向量对离心泵的状态进行故障诊断是可行的；RBF神经网络的分类性能较好，能够有效的进行离心泵故障诊断。研究结果表明本方法用于离心泵故障诊断有较高效率，诊断正确率可达100%。