非平稳随机过程功率谱与自相关的关系推导

胡敬安 魏冬梅

(山东师范大学物理与电子科学学院，山东 济南 250014)

0 引 言

佩利-维纳准则指出平稳随机过程的功率谱密度与自相关函数是1对傅立叶变换，一般涉及随机过程的教材或书籍通常都会介绍佩利-维纳准则，有的直接给出结论[1-3]，也有很多教材会同时给出该结论的推导过程以帮助理解[4-8]．但很少有文献介绍非平稳随机过程的功率谱密度与自相关函数的关系，文献[9-10]也仅仅介绍了一类特殊的非平稳随机过程：循环平稳随机过程的功率谱与自相关的关系．循环平稳随机过程的自相关函数R(t,t+τ)对时间(t)具有周期性，将其在1个周期内对t进行平均即可蜕变为一元函数R(τ)，然后取傅立叶变换即为循环平稳随机过程功率谱，即

(1)

式中F表示求傅立叶变换，Pξ(f)为随机过程的功率谱密度，T0为自相关函数R(t,t+τ)对t的周期．文献[9-10]只是给出了结论，没有导出过程，这可能令初学者感到困惑．鉴于此，本文将对非平稳随机过程的功率谱与自相关函数的关系进行推导．

1 结论的导出

随机过程的功率谱密度定义为所有样本函数的功率谱密度的统计平均．记随机过程为ξ(t)，其功率谱密度为Pξ(f)，则

(2)

其中ΞT(f)为截取过程

的傅立叶变换．式(2)中|(ΞT(f)|2可表示为

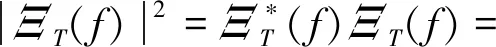
将其变为二重积分可得

(3)

式(3)的积分区域Dt1t2如图1所示．

图1 积分区域Dt1t2

记t1=t，令t2-t1=τ，则式(3)积分变为

其中积分区域(Dtτ)如图2所示．于是

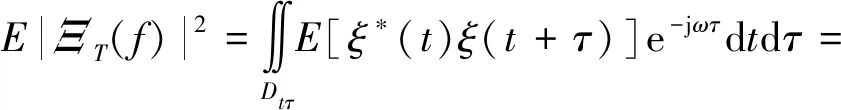
将其带入式(2)可以得到

(4)

由式(4)可以看出，随机过程的功率谱为其自相关函数的二重广义积分．

图2 积分区域Dtτ

现将图2中Dtτ以t轴为界分为上下2个部分，先对t积分，再对τ积分，则式(4)可变为2个广义二次积分

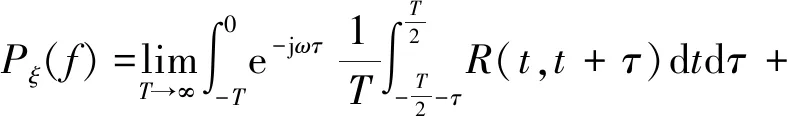
将2个广义二次积分先对t的积分求极限，再对τ的积分求极限

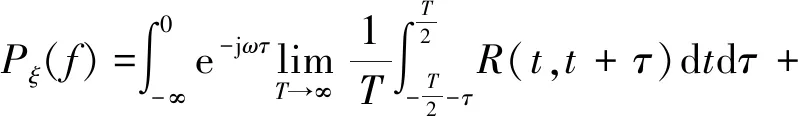
(5)

应注意到式(5)中对t的2个广义积分相等，即

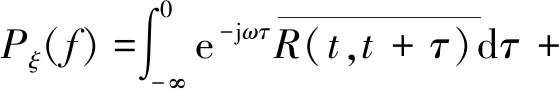
(6)

即随机过程的功率谱密度是其自相关函数的时间平均的傅立叶变换．

2 讨 论

式(6)所给结论不仅对平稳随机过程、还对包括循环平稳随机过程在内的非平稳过程都是成立的．当随机过程为广义平稳随机过程时，其自相关函数R(t,t+τ)与t无关，即其蜕变为一元函数R(τ)，所以R(t,t+τ)的时间平均就是R(τ)自身，此时有

即平稳过程的功率谱密度为R(τ)的傅立叶变换，因此佩利-维纳准则只是式(6)所给结论的1个特例．

而对于循环平稳随机过程，其自相关函数R(t,t+τ)对t具有周期性，其在1个周期内的平均等于整个时间范围内的平均，即有

其中T0为自相关函数R(t,t+τ)对t的周期，故

因此描述循环平稳过程功率谱与自相关关系的式(1)也只是本文结论式(6)的1个特例．

另外，如果对自相关函数R(t,t+τ)不进行时间平均，直接针对变量τ进行傅立叶变换，结果将同时也是t的函数，如式(7)所示

Fτ[R(t,t+τ)]=Pξ(t,f)，

(7)

式中Fτ表示针对变量τ进行傅立叶变换．现将Pξ(t,f)在整个频率范围内积分，则有

即Pξ(t,f)对频率的积分为ξ(t)的瞬时功率的统计平均值，因此Pξ(t,f)可定义为随机过程的瞬时功率谱，则有

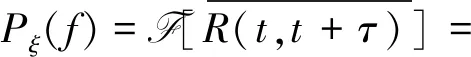
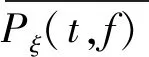
3 总 结

本文从随机过程功率谱密度的定义出发导出了随机过程功率谱与平均自相关是1对傅立叶变换的结论，不管是描述平稳随机过程的功率谱与自相关关系的佩利-维纳准则，还是描述循环平稳随机过程的功率谱与自相关关系的式(1)，都可看成是本结论的1个特例．