三次DP 曲线定义区间的扩展及其形状优化
2020-04-21张迪查东东刘华勇
张迪,查东东,刘华勇
(安徽建筑大学数理学院,安徽合肥230601)
在计算机辅助几何设计中(computer aided geometric design,简称CAGD),针对自由曲线曲面的研究一直受到研究者的广泛关注。通常利用基函数与控制顶点的线性组合来构造曲线,如果给定控制顶点,那么相应的曲线就随之被确定。若要改变曲线曲面的形状,必须调整其控制顶点,此过程较为烦琐复杂,在实际工程中并不可取。基于此,研究者通过在曲线中引入权因子,提出了有理形式的曲线曲面,这类曲线曲面在不改变其控制顶点的情况下可通过改变权因子来修改曲线的形状。较著名的方法有非均匀有理B 样条(NURBS)以及有理Bézier方法等[1]。经过几十年的发展,NURBS 方法已趋于成熟,逐渐成为曲线曲面造型中较为流行、实用的技术。但由于其描述方法和计算复杂,如权因子选取不便,参数化、曲面连续性、求导次数增加等问题,使得NURBS 方法在工程曲线曲面中的应用优势难以充分发挥,影响其实用性[2]。
随着几何造型工业的发展,曲线造型对曲线的灵活性、形状可调性、逼近性和描述能力提出了更高的要求。为了更加灵活地调控曲线曲面的形状,通过引入形状参数对现有方法进行扩展,可以得到形状可调的曲线曲面。拓展后的曲线曲面不仅可以继承原曲线曲面的优良性质,利用形状参数还可以有效改变曲线的形状或位置,增加曲线的灵活性、形状可调性、逼近性和描述能力等。此方法较为直观,且计算复杂度大幅降低,求导较NURBS 方法方便,不会遇到权因子选取等难题。
2003 年,韩旭里等[3]通过提升B 样条基函数次数的方法,提出了带有一个形状参数的三次均匀B样条曲线。2006 年,吴晓勤[4]利用De Casteljau 递归法为Bézier 曲线引入了形状参数。同年,吴晓勤等[5]针对四次Bézier 曲线扩展了2 种不同的类型。2007年,基于不同的调配函数,徐岗等[6]得到了2 种带局部形状参数的分段多项式曲线的定义。2011 年,刘华勇等[7]定义了一种新的带形状参数的四次Ball 基函数,将传统四次Ball 曲线进行了推广。近年来,因几何造型发展的需要,陆续在多项式空间中构造出一些新型曲线,或者将几种不同的构造方法进行组合,得到的结果同样可喜。
本文着重介绍一种新型参数曲线,即DP 曲线。DP 曲线相关理论由DELGADO 等[8-9]提出。实践证明,这种新型DP 曲线具有很好的端点插值性、稳定性、曲线保形性、线性计算复杂度等优良性质。但是DP 曲线与传统的Bézier 曲线类似,在给定控制顶点时缺乏形状可调性。为克服此缺陷,2011 年,陈杰等[10]将形状参数引入DP 曲线并讨论其相关性质。2012 年,陈福来等[11-12]定义了一组新的含参基函数,构造并分析了一类广义三次DP 曲线的定义、性质及其形状特点。2018 年,彭兴璇等[13]利用在端点切向量处引入调节参数的方法,最终得到一组带有张力参数α 和偏移参数β 的基函数,构造了一类带形状参数的三次DP 曲线。然而文献[3-7,11-13]均是针对特定次数的曲线所做的拓展。文献[8-9]中,DP曲线的形状由给定控制点确定,缺乏形状调节或修改的功能。陈杰等[10]也仅仅给出了DP-NTP 曲线的定义,并没有论证DP-NTP 曲线的光滑拼接条件。
针对DP 曲线缺乏形状可调性这一缺陷,本文构造了一种带形状参数的三次DP 基并利用新基构造含参曲线,增加了DP 曲线的灵活性。主要思想:将三次DP 基函数的定义区间由[0,1]推广为[0,α],根据三次DP 基函数的端点性质,重新参数化[14]后提出了一种带形状参数的三次DP 曲线。在形状参数取特定值时,新三次DP 基函数可以退化为DELGADO 等 提 出 的 三 次DP 基[8-9]。形 状 参 数α 为三次DP 曲线提供了独立于其控制顶点外的自由度,使新三次DP 基函数在继承了一般三次DP 基优良性质的同时(如端点性质、凸包性、仿射不变性、变差缩减性等),仍具有形状修改的功能。另外,根据这种方法可以在任意次DP 基函数中引入形状参数。
1 三次α-DP 基的构造及其性质
1.1 三次α-DP 基的构造及定义
首先由三次DP 基函数(0≤t ≤1):
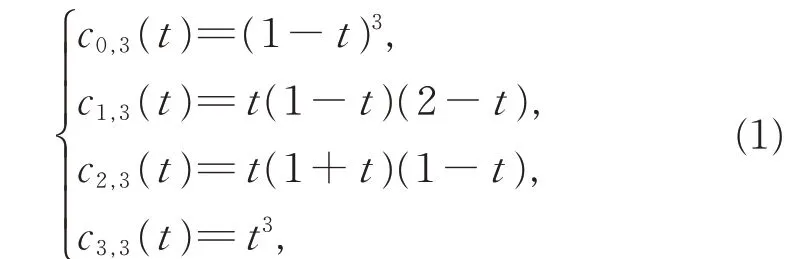
得到其端点性质:
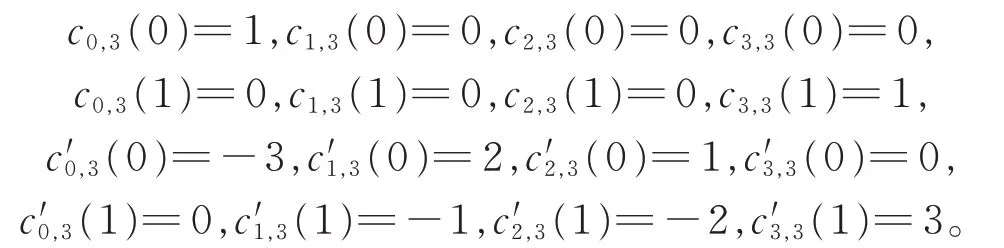
将式(1)中变量t 的定义区间由[0,1]拓展为[0,α](0<α≤1),可构造出一种带有形状参数α 的三次DP基函数,具体构造过程如下:
为了构造新三次DP 基,设
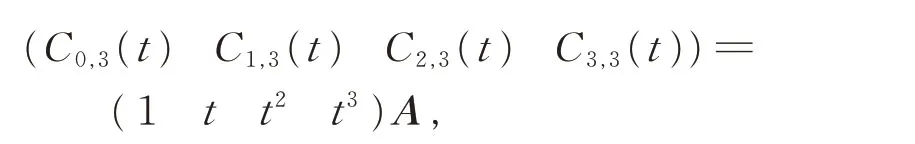
其中,0≤t≤1,0<α≤1,且A 为一个待定的4 阶方阵。由上式可得
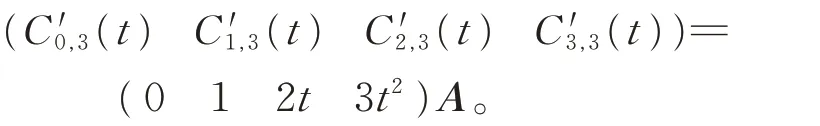
为了使得新三次DP 基函数在端点处的性质与三次DP 基相同,有

将式(2)记为B=CA。计算可得

故
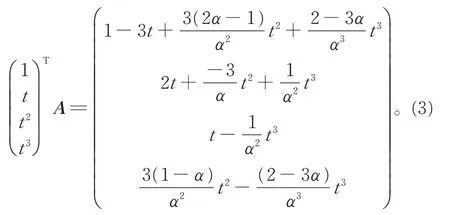
令t=αu(0≤u≤1,0<α≤1),对式(3)重新参数化,整理后有
定义1对于0≤u≤1,0<α≤1,关于变量u 的函数:
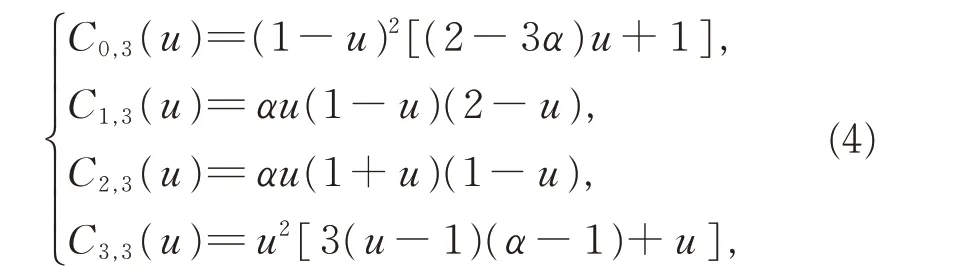
称为带有形状参数α 的三次DP 基函数,简称为三次α-DP 基。
图1 给出了形状参数α 分别取不同值时的基函数图形。(a)~(d)分别为固定α=0.5,0.6,0.8,1 时的基函数图形。改变α 值时,4 条基函数的形状均受影响,可以整体修改曲线的形状。
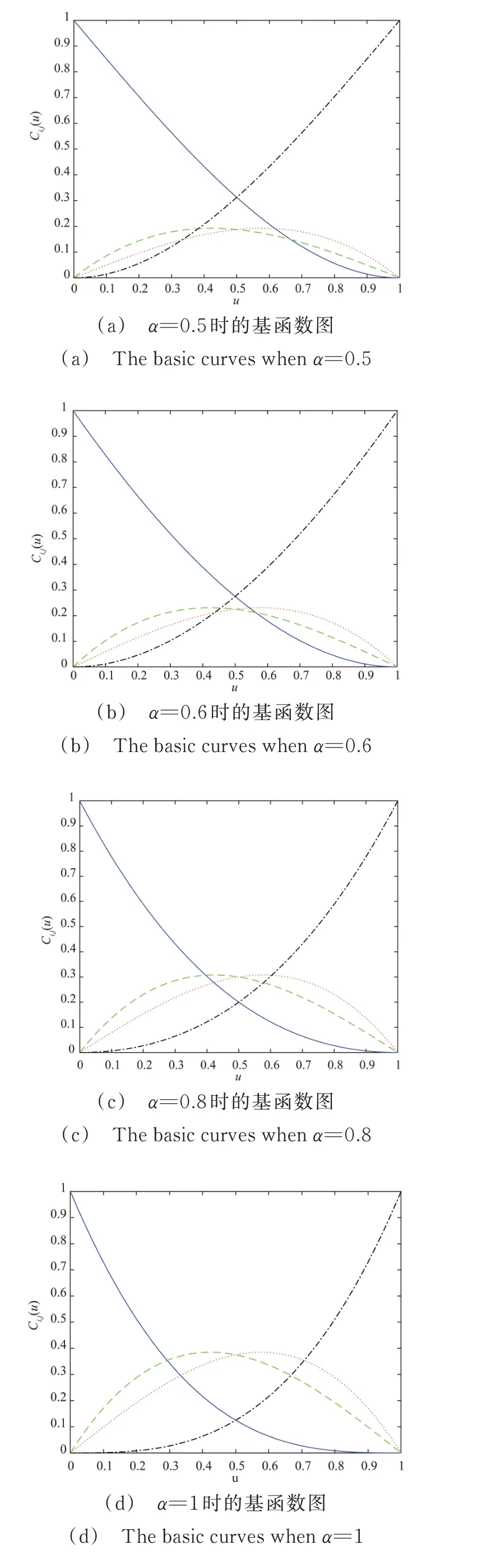
图1 参数取不同值时的三次DP 基函数Fig.1 The cubic α-DP basic curves with different parameters
1.2 三次α-DP 基函数的性质及证明
(ii)非负性:Ci,3(u)≥0(i=0,1,2,3)。
(iii) 对 称 性 :Ci,3(u)=C3-i,3(1-u)(i=0,1,2,3)。
(iv)单调性:固定变量u(0≤u≤1),对α 求导,可得C0,3(u)与C3,3(u)是关于参数α 的递减函数;C1,3(u)与C2,3(u)是关于参数α 的递增函数。
(v)端点性质:
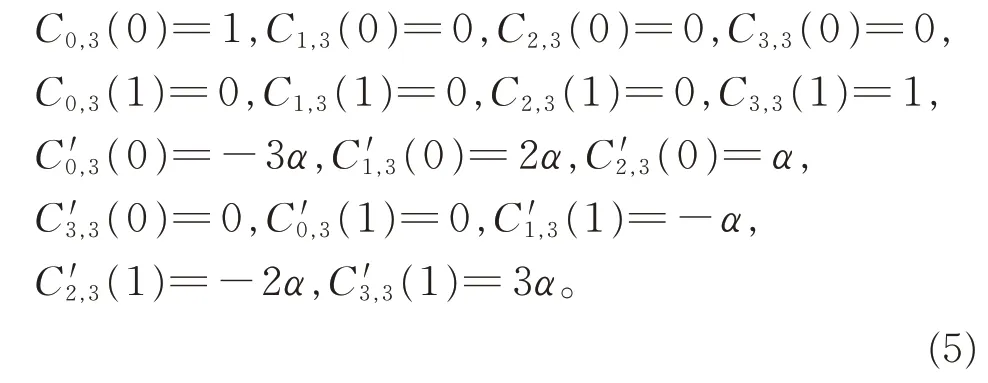
(vi)单峰性:Ci,3(u)(i=0,1,2,3)在区间[0,1]上仅有一个最大值。
(vii)退化性:显然,将α=1 代入式(1)时,三次α-DP 基退化为文献[8-9]中的三次DP 基函数。因此,三次α-DP 基是对三次DP 基函数的一种含参扩展。
下面对三次α-DP 基函数的相关性质进行证明。
证明(i)由式(4)可得
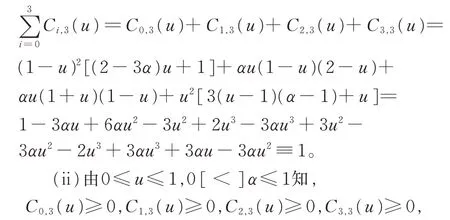
即Ci,3(u) ≥0(i=0,1,2,3)。
(iii)由式(4)可得
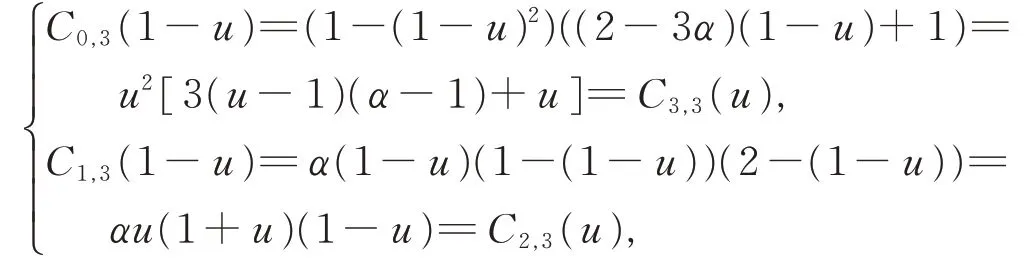
即Ci,3(u)=C3-i,3(1-u)(i=0,1,2,3)。
(iv)固定变量u(0≤u≤1),对α 求导:
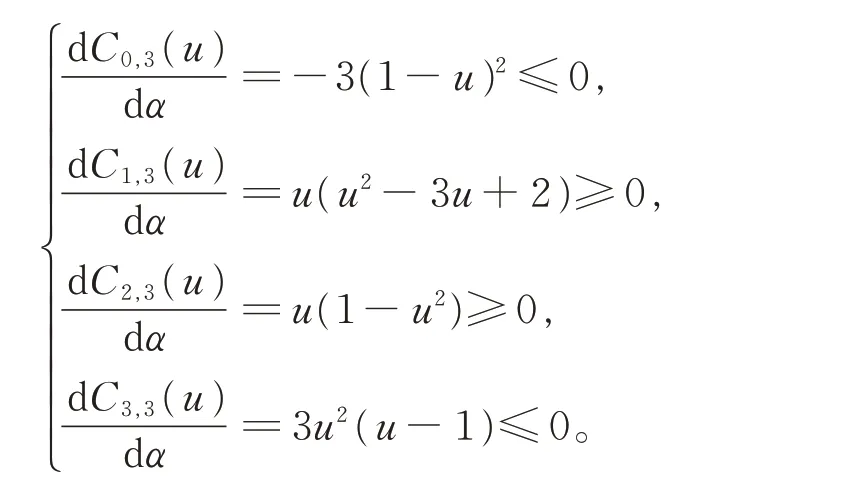
因此,固定变量u,C0,3(u)与C3,3(u)是关于参数α 的递减函数;C1,3(u)与C2,3(u)是关于参数α 的递增函数。
(v)对变量u 求导,其一阶和二阶导数分别为:
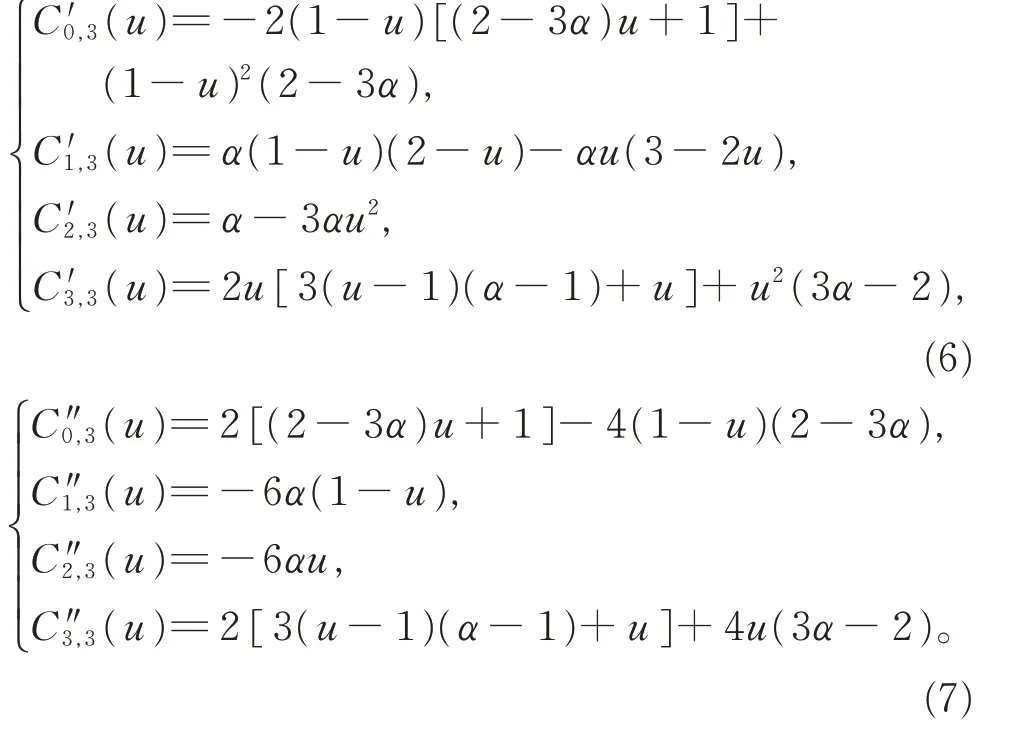
对式(6)进行简单计算,可得其端点性质式(5)。
2 带形状参数的三次α-DP 曲线
2.1 带形状参数的三次α-DP 曲线的定义及性质
根据带形状参数的三次α-DP 基函数,给出曲线的定义。
定义2对于0≤u≤1,0<α≤1,给定4 个控制顶点pi∈Rd(i=0,1,2,3,d=2,3),称曲线
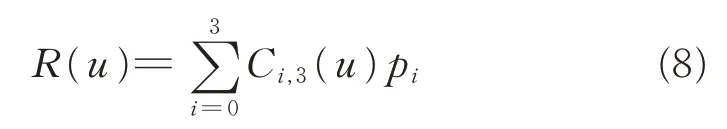
为带形状参数的三次DP 曲线,简称三次α-DP 曲线。 其中Ci,3(u)(i=0,1,2,3)为式(4)定义的三次α-DP 基函数。
三次α-DP 曲线具有以下性质:
(i)端点性质。
由基函数的端点性质可知,三次α-DP 曲线同样具有以下优良性质:
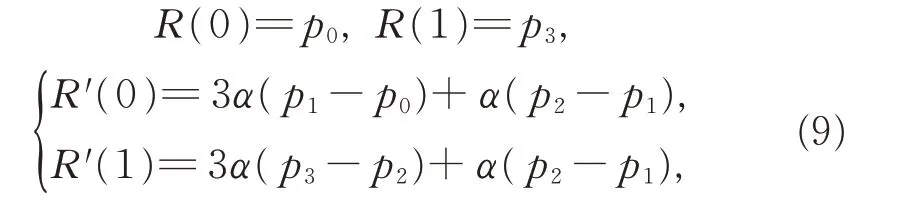
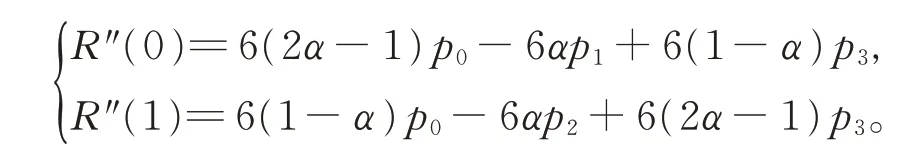
(ii)凸包性。
由基函数(4)的规范性和非负性知,由定义2 生成的曲线完全位于由其控制顶点pi(i=0,1,2,3)所形成的凸包内。
(iii)几何不变性与仿射不变性。
由于所定义的式(8)是参数化方程,当形状参数α 固定时,三次α-DP 曲线的形状、位置与如何选取坐标系无关,仅取决于曲线的控制顶点pi(i=0,1,2,3)。即
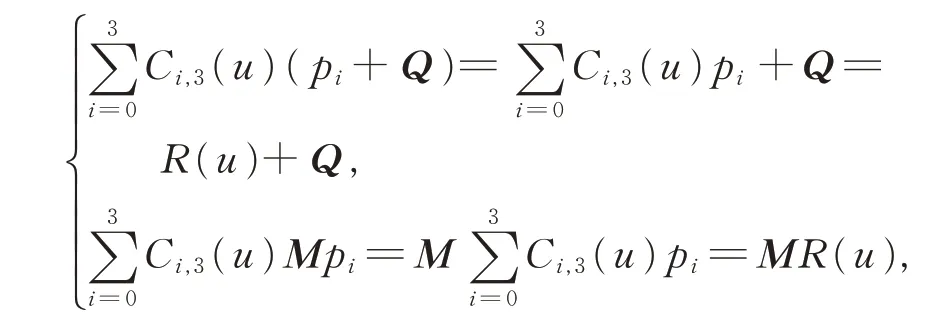
其 中,Q 是 任 意 向 量 且Q ∈Rd(d=2,3),M 是 一 任意k×k(k=2,3)阶矩阵。
(iv)对称性。
当给定形状参数α 的取值时,由基函数的对称性可知,由2 个仅顺序不同的控制多边形与三次α-DP 基函数组合后所生成的2 条曲线的形状是完全相同的,仅方向相反。即
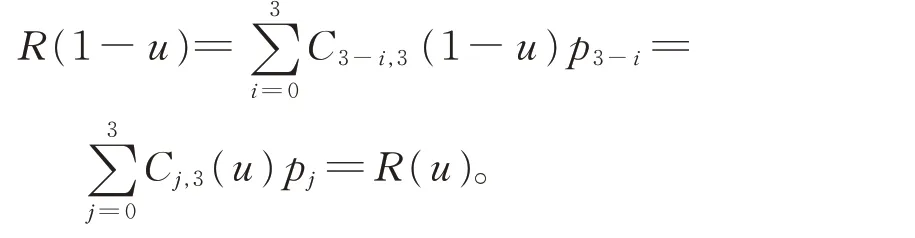
(v)退化性。
由基函数的退化性可得三次α-DP 曲线的退化性。当α=1 时,三次α-DP 曲线退化为三次DP曲线。
(vi)形状可调性。
形状参数α 为三次α-DP 曲线提供了一个独立于控制顶点之外的自由度。三次α-DP 曲线的形状可以通过改变参数α 的取值来调整,并且此过程中控制顶点仍保持不变。
图2 为参数分别取不同值时的三次α-DP 曲线,其中点划线代表α=0.6,实线代表α=0.8,虚线代表α=1。
2.2 形状参数α 的几何意义
从数值和图形两个角度对形状参数的几何意义进行分析。
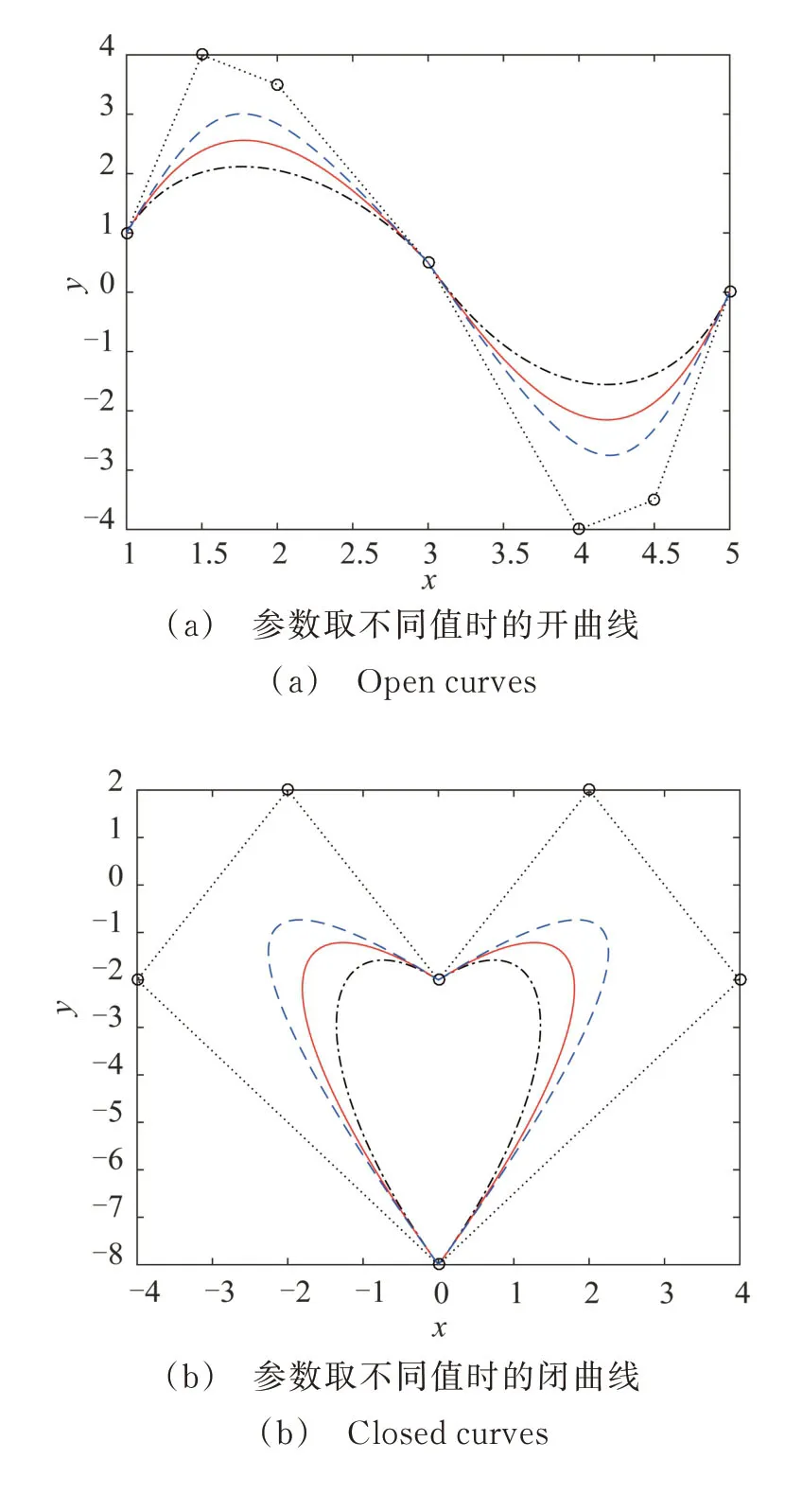
图2 参数取不同值时的三次α-DP 曲线Fig.2 The cubic α-DP curves with different parameters
确定形状参数α 的值与曲线R(u)形状之间的关系。由三次α-DP 基函数的定义及其性质可知,固定变量u,当参数α 逐渐增大时, C0,3(u) 与C3,3(u)逐渐减小,C1,3(u)与C2,3(u)逐渐增大。即随参数α 的增大,曲线的弯曲程度随之增大,三次α-DP 曲线逐渐向其控制多边形靠近。
将式(8)改写为矩阵形式:
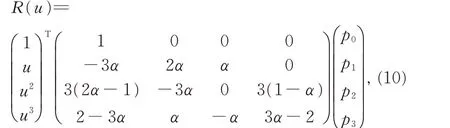
由控制顶点q0q1q2q3所确定的三次Bézier 曲线B3(u)可表示为
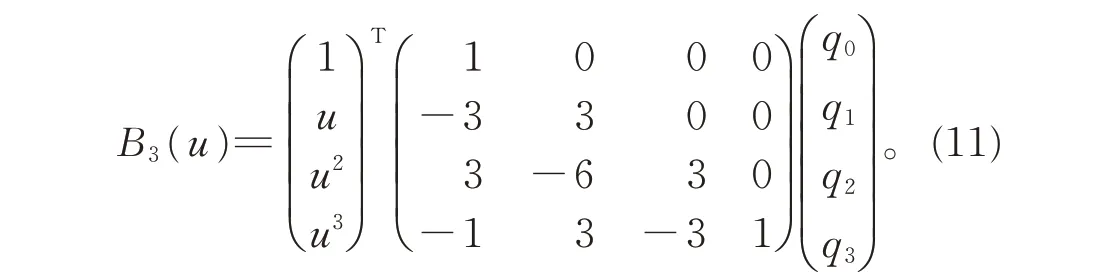
二者控制顶点之间的关系为
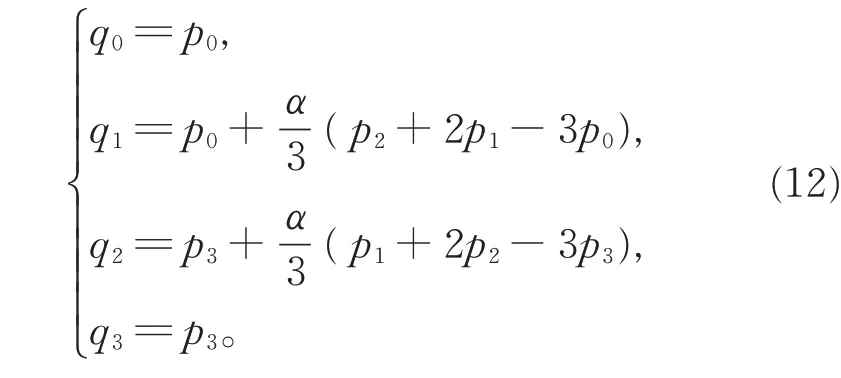
由式(12)可知,三次Bézier 曲线B3(u)的各控制顶点的数值大小与三次α-DP 曲线R(u)的控制顶点的数值大小正相关。即形状参数α 取值越大,二者数值就越接近,三次α-DP 曲线向三次Bézier 曲线不断接近。因此,根据三次Bézier 曲线的逼近性可推断:形状参数α 越大,三次α-DP 曲线越接近其控制多边形。
图3 直观地展示了形状参数α 对曲线的影响规律,其中,红色实线代表三次Bézier 曲线,同时也是退化之后的三次DP 曲线。2 条黑色、绿色曲线则分别代表α=0.6,α=0.8 时的三次α-DP 曲线,图中星状点与空心圆状点分别为Bézier 曲线、三次α-DP 曲线的控制顶点。
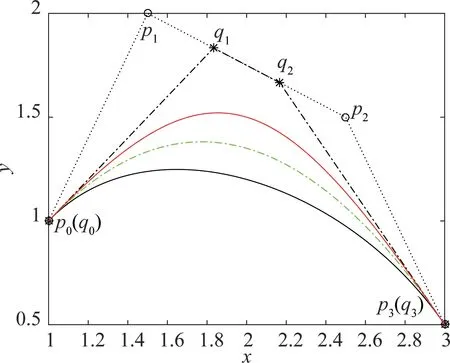
图3 形状参数α 的几何意义Fig.3 The geometric meaning of shape parameter
2.3 带形状参数的三次α-DP 曲线拼接
在复杂的自由曲线曲面设计中,单一的曲线段已不能满足几何造型设计的要求,因此曲线的拼接必不可少。下面讨论带形状参数的三次α-DP 曲线的拼接条件。
设2 条相邻的三次α-DP 曲线表达式分别为:
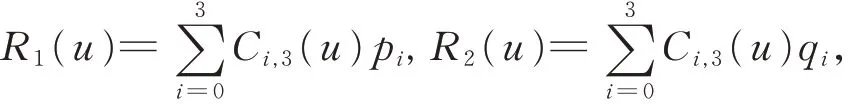
其中i=0,1,2,3,p0p1p2p3和q0q1q2q3分别为曲线R1(u)和R2(u)的控制顶点,形状参数分别为α1和α2。
定理1当给定0≤u≤1,0<α≤1 时,若2 条相邻的三次α-DP 曲线G0和G1连续,需满足
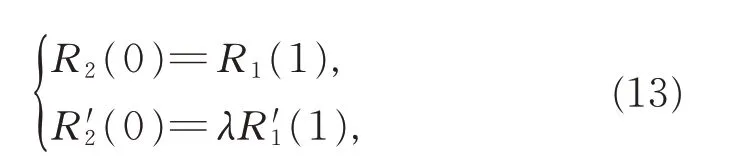
证明 由式(9)知,
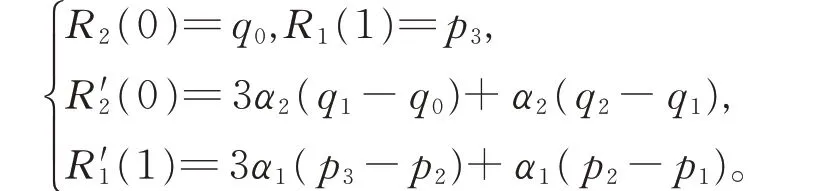
若2 段三次α-DP 曲线G0和G1连续,则有
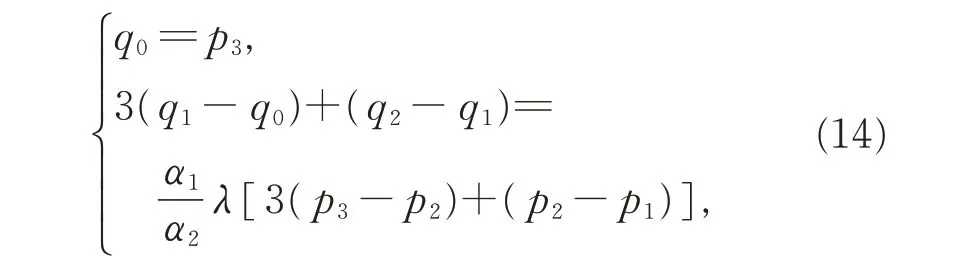
化简可得式(13)。此时,2 条相邻的三次α-DP 曲线不仅满足G0连续,在连接点处达到G1连续。且当λ=1,即δ= α1α2时,在 连 接 点 处 两 切 矢 相 等:R′1(1)=R′2(0),2 段曲线达到C1连续。
下面讨论相邻三次α-DP 曲线段之间G2连续的条件。
定理2若2 条相邻的三次α-DP 曲线G2连续,2 条曲线需满足G1连续条件,且曲率相等:
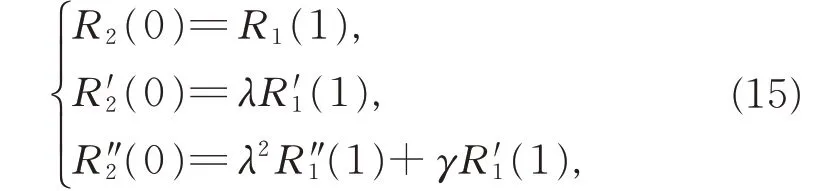
其中,λ= δα2α1,δ 为非负常数。γ 满足γL1=L2。
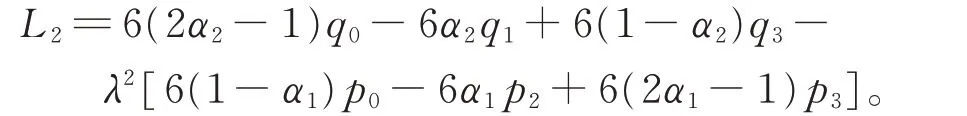
证明2 条曲线的曲率为
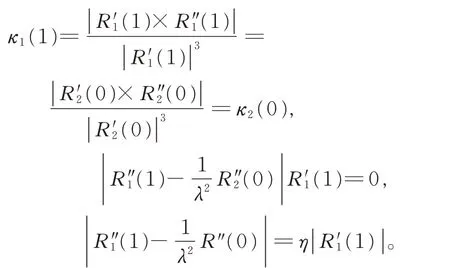
根据曲线的端点性质,计算得
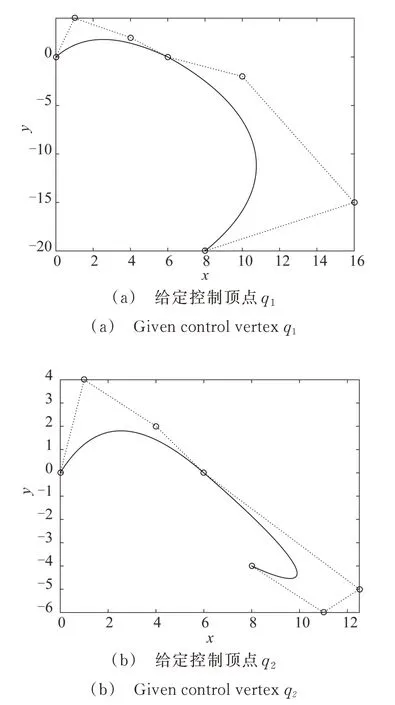
图4 G1连续的两曲线段拼接Fig.4 Construction of the curves with G1 continuous conditions
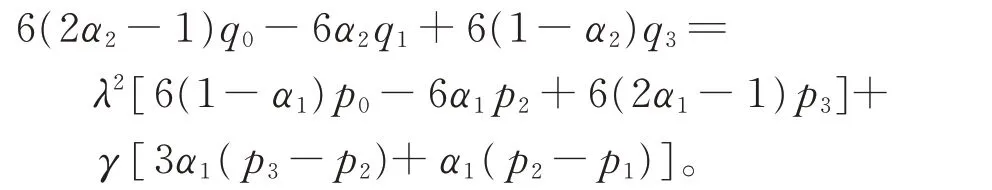
由G1连续条件以及式(15),即可给出相邻两段曲线G2连续的拼接条件。
下面给出不同连续条件下,三次α-DP 曲线的光滑连续拼接的数值实例。
给定控制顶点p0(0,0), p1(1,4), p2(4,2),p3(6,0),q0(6,0),q1(10,-2),q3(8,-20)。由G1的连续条件计算q2(16,-15),取λ=δ=0.5,α1=α2=0.8,作图4(a)。
给定控制顶点 p0(0,0),p1(1,4),p2(4,2),p3(6,0),q0(6,0),q2(11,-6),q3(8,-4)。由G1的连续条件计算q1(12.5,-5),且取λ=δ=0.5,α1=α2=0.8,作图4(b)。
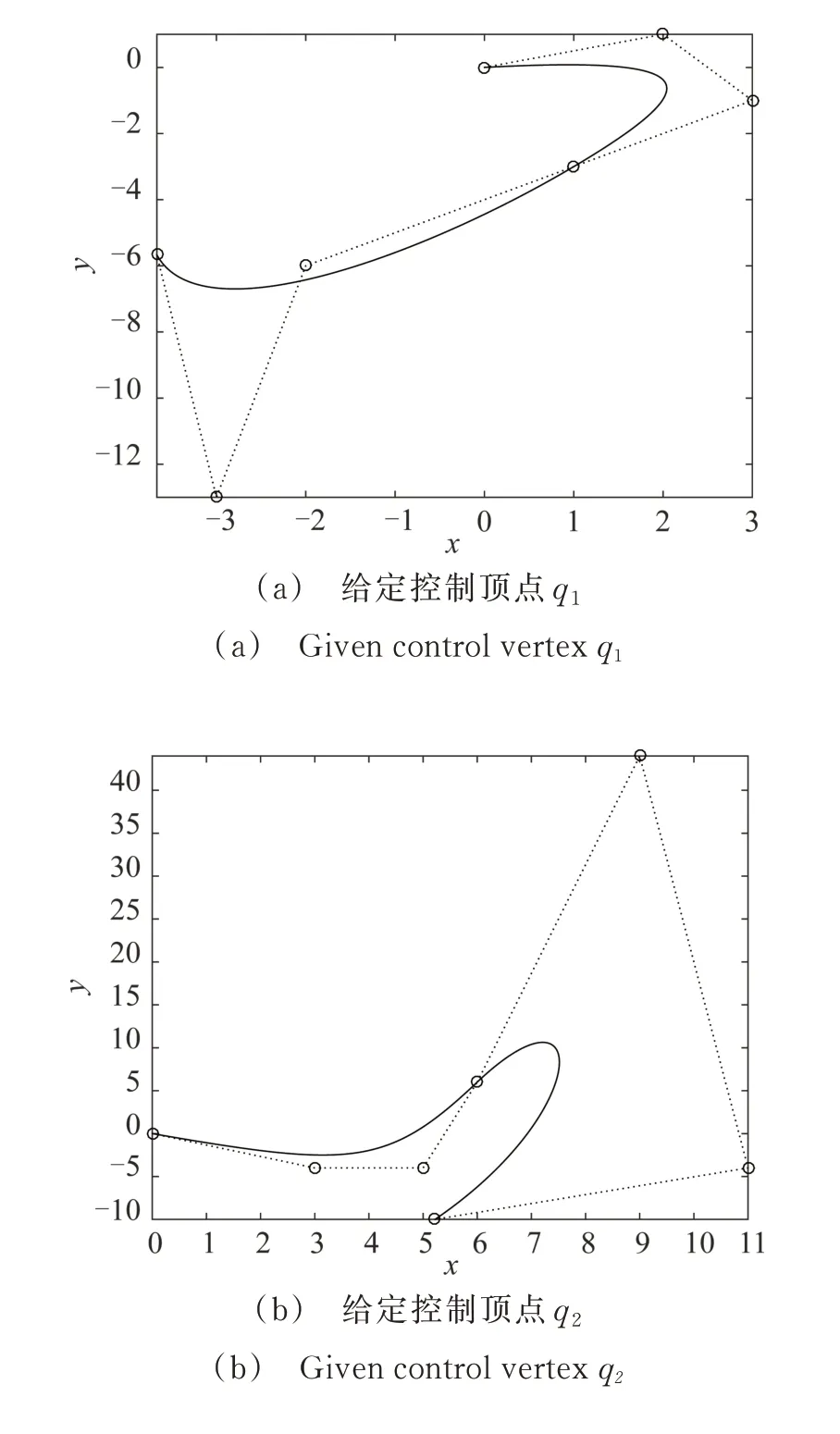
图5 G2连续的两曲线段拼接Fig.5 Construction of the curves with G2 continuous conditions
给定控制顶点p0(0,0),p1(2,1),p2(3,-1),p3(1,-3),q0(1,-3),根据曲线G1和G2的连续条件计算q1(-2,-6), q2(-3,-13), q3(-3.667,-5.667),取α1=1,α2=0.5,δ=2,γ=1,作图5(a)。
给定控制顶点p0(0,0),p1(3,-4),p2(5,-4),p3(6,6),q0(6,6),根据曲线G1和G2的连续条件计算q1(9,44),q2(11,-4),q3(5.22,-10),取α1=1,α2=0.576,δ=2.5,γ=-3.48,作图5(b)。
图6 给出G1连续条件下,取不同参数时的旋转面。
3 带形状参数的三次α-DP 曲面
3.1 带形状参数的三次α-DP 曲面的定义及性质
运用张量积方法将三次α-DP 曲线推广到曲面,给出带形状参数的三次α-DP 曲面的定义。
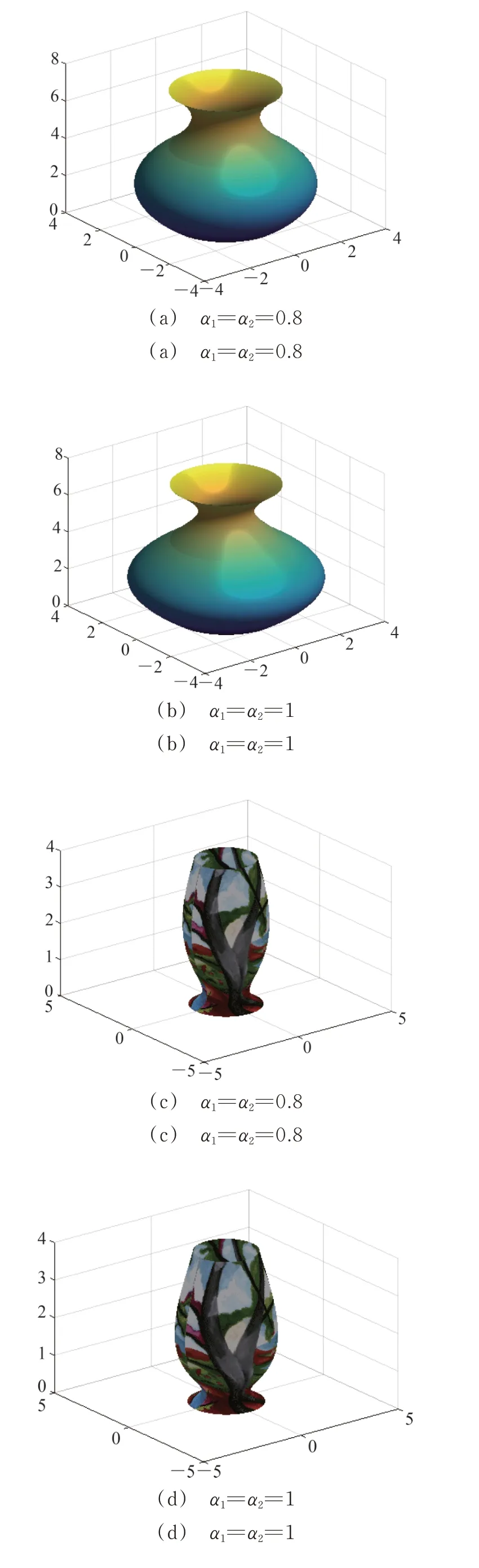
图6 不同参数下G1连续的旋转面Fig.6 Rotating surfaces in G1 continuous case with different parameters
定 义 3给 定 4×4 个 控 制 顶 点 pij(i=0,1,2,3),对于0≤u,v≤1,0<α≤1,称张量积曲面
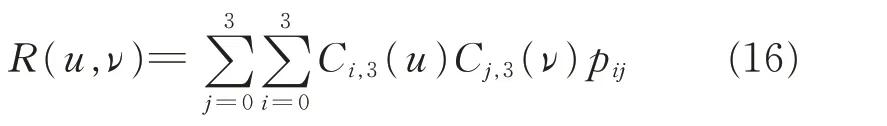
为带形状参数的三次DP 曲面,简称三次α-DP 曲面。 其中Ci,3(u),Cj,3(ν)(i=0,1,2,3)为式(4)定义的三次α-DP 基函数。
图7 为形状参数取1 时,三次α-DP 开曲面和闭曲面的构造。
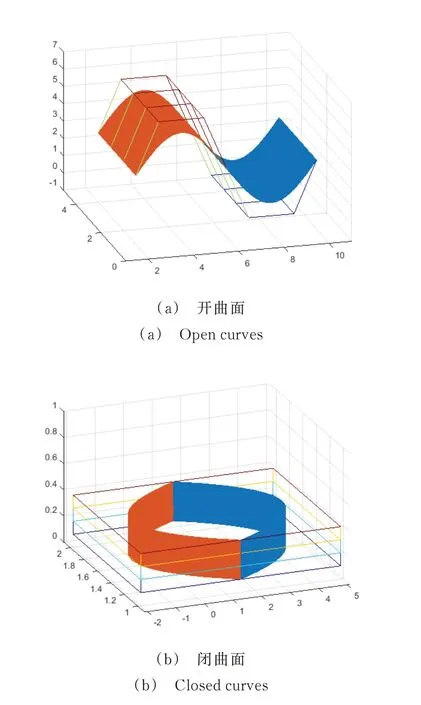
图7 带形状参数的三次α-DP 曲面的构造Fig.7 The cubic α-DP surfaces structure with a parameter
三次α-DP 曲面具有下列性质:
(i)凸包性。
三次α-DP 曲面位于控制网格pij(i=0,1,2,3)所形成的凸包内。
(ii)几何不变性和仿射不变性。
三次α-DP 曲面是参数化曲面,位置和形状仅仅取决于曲面的控制网格,与其他形状参数或坐标系无关。若要对曲面作变换,只需对其控制网格pij作变换即可。
(iii)对称性。
由三次α-DP 基函数的对称性可知,颠倒控制网格pij所形成的新曲面与原三次α-DP 曲面相同,仅方向相反。即
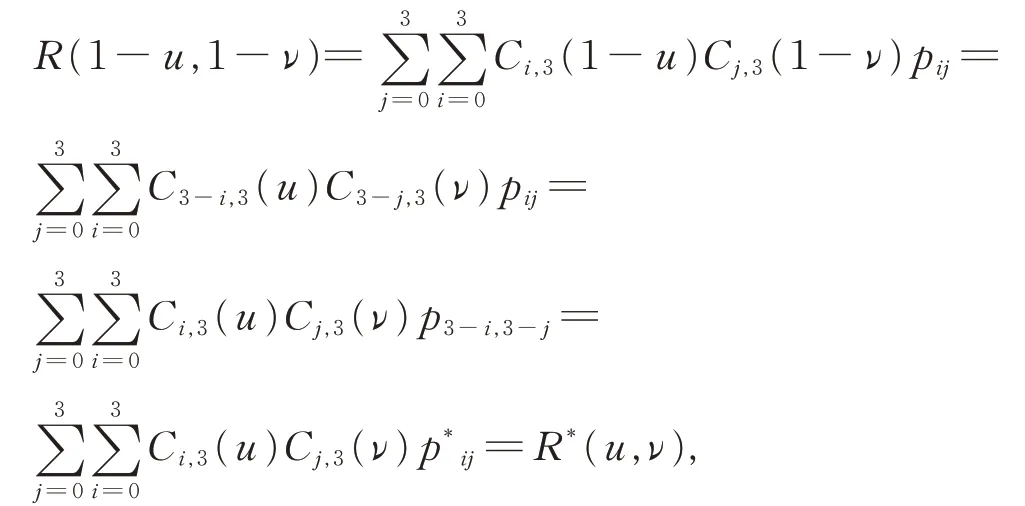
R*(u,ν)与R(u,ν)表示的是同一曲面,方向相反。
(iv)边界性质。

(v)形状可调性。
固定三次α-DP 曲面的控制网格pij,可通过调节形状参数αu和αv的值来调节三次α-DP 曲面的形状。图8 给出了αu和αv取不同值时的曲面形状。
3.2 带形状参数的三次α-DP 曲面拼接
对于0≤u,v≤1,0<α≤1,设2 条相邻的三次α-DP 曲面表达式为:
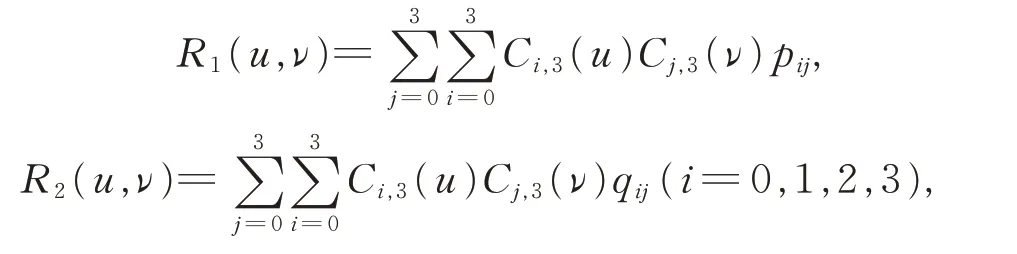
其中,pij和qij分别为曲线R1(u,ν)和R2(u,ν)的控制网格,形状参数分别为αu1,αv1和αu2,αv2。
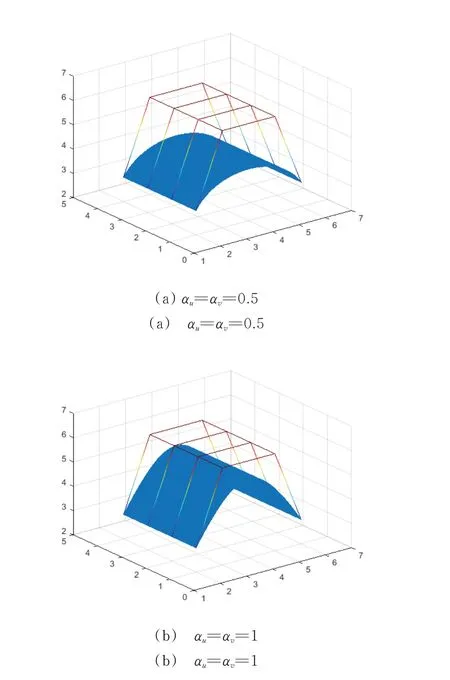
图8 参数取不同值时的三次α-DP 曲面Fig.8 The cubic α-DP surfaces with different parameters
定理3当给定0≤u,v≤1,0≤αu,αv≤1 时,2条相邻的三次α-DP 曲面G0和G1连续,需满足
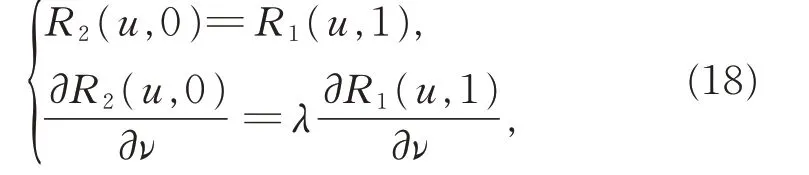
其中,λ= δαν2αν1,δ 为非负常数。
证明由式(17)可得:
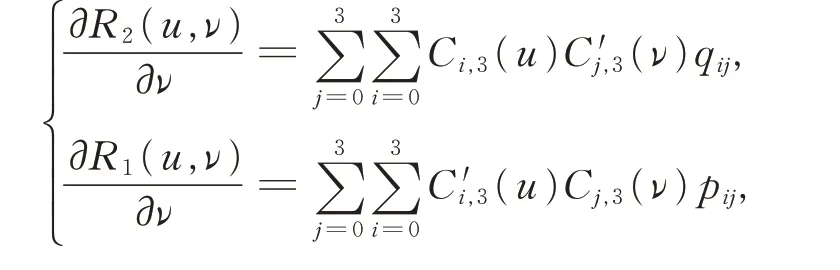
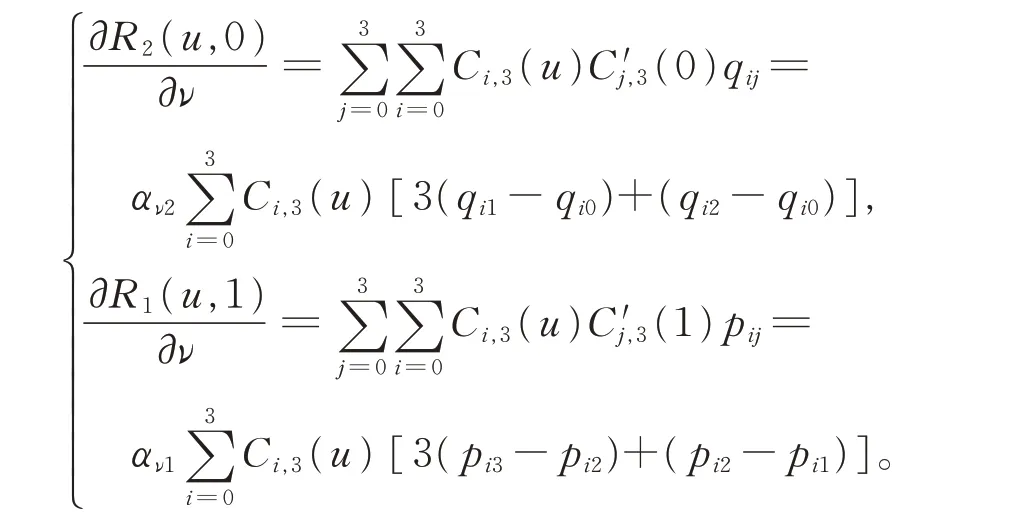
由式(18),有
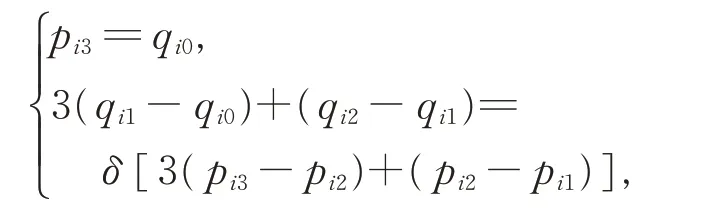
其 中,λ= δαν2αν1,δ 为非负常数,化简即可证得。此时2 条相邻三次α-DP 曲面片既满足位置连续,在连接点处又具有同向切矢。
下面讨论2 条相邻的三次α-DP 曲面片G2连续的条件。
定理4若2 条相邻的三次α-DP 曲面G2连续,要求两曲面片不仅在拼接点处G1连续,而且曲率相等,即
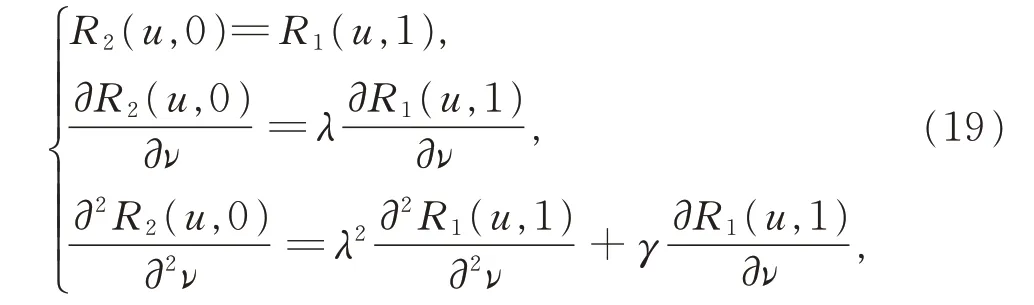
式中,λ= δαν1αν2。γ 满足γLν1=Lν2,其中,
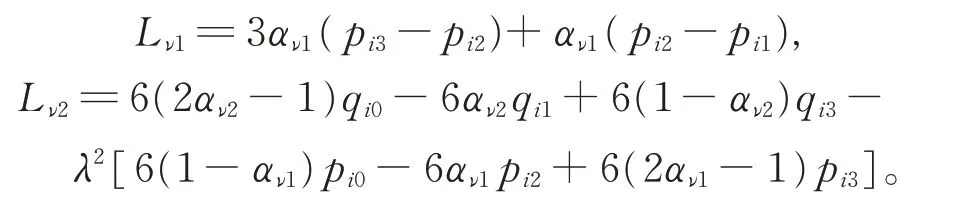
4 形状参数的选择
采用文献[15]中的能量函数,对第i 段曲线有
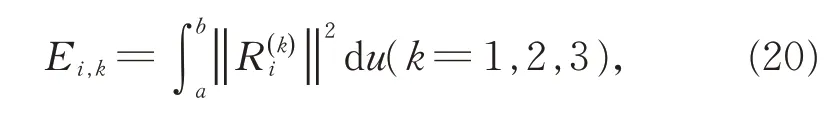
假定a=0,b=1。当k=1 时,能量函数是拉伸能量的近似,Ei,1反映曲线长度;当k=2 时,能量函数是弯曲能量的近似,Ei,2反映曲线的曲率;当k=3 时,能量函数是扭曲能量的近似,Ei,3反映曲线曲率的变化量。
定理5给定第i 段曲线的控制顶点pi,j(i=1,2,…,n,j=0,1,2,3),使整条取最小值的参数αi需满足
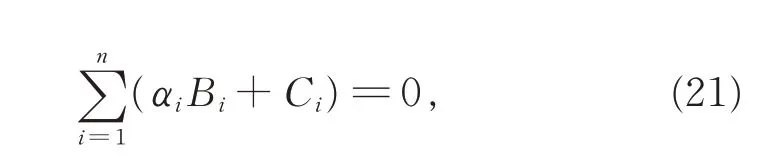
其中,
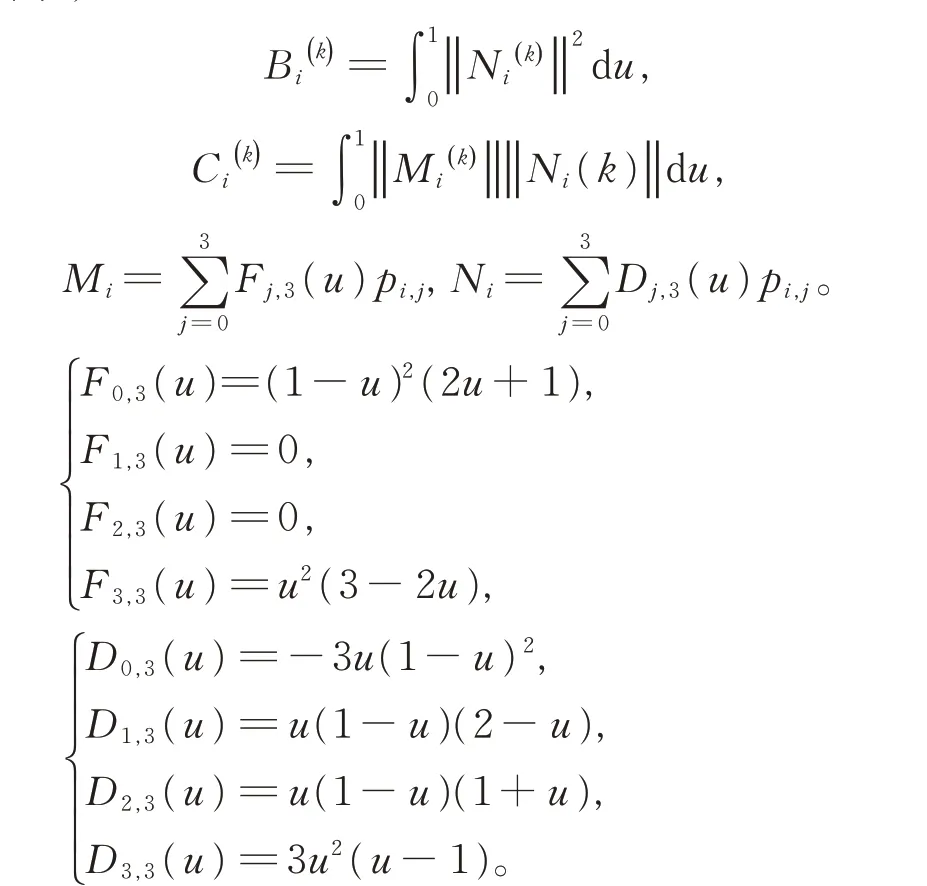
证明首先对第i 段曲线优化。
已知式(4),令
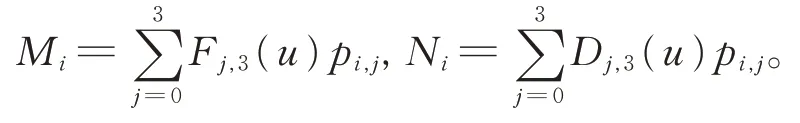
将式(4)和(8)改写为:
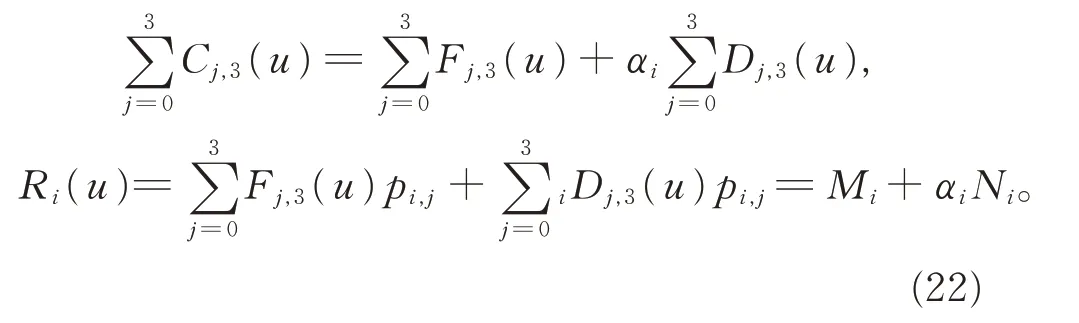
对式(22)求k 阶导数,可得
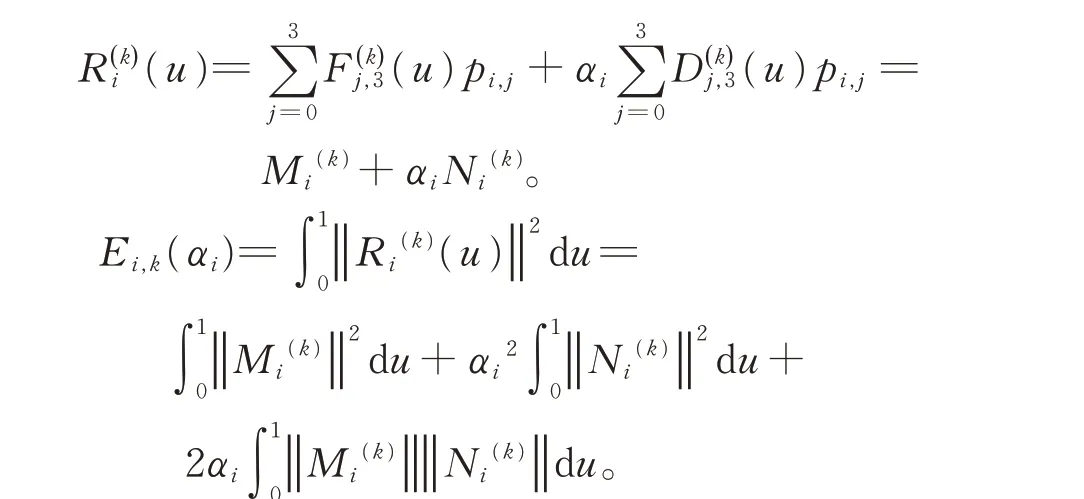
记
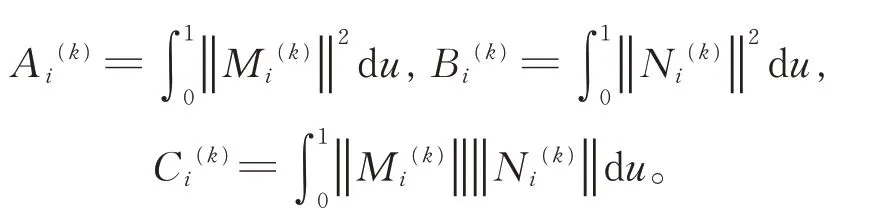
可将第i 段曲线的能量函数改写为
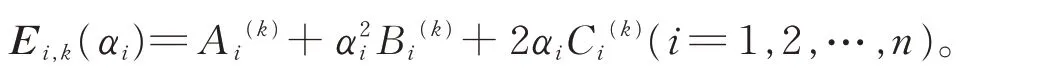
对由n 段三次α-DP 曲线拼接而成的整条G1连续曲线进行优化。为了在保证曲线段保持G1连续的同时,能够确保形状参数的最优取值,给出目标函数:其中,k(k=1,2,3)为能量函数的阶数,αi(0<αi≤1)为第i(i=1,2,…,n)段的形状参数。
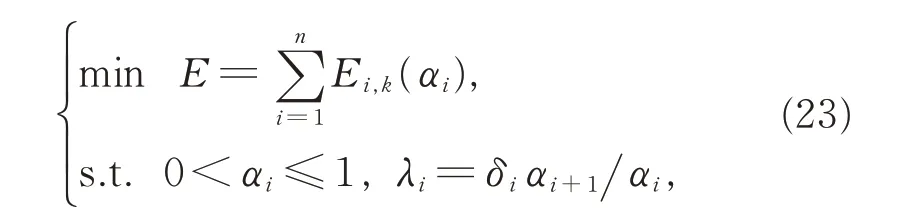
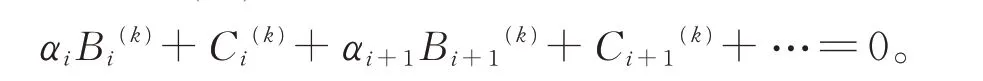
求解式(23),即得证。
图9 给出的是利用3 种形状参数选取方案构造出满足不同要求的三次α-DP 曲线的实例。
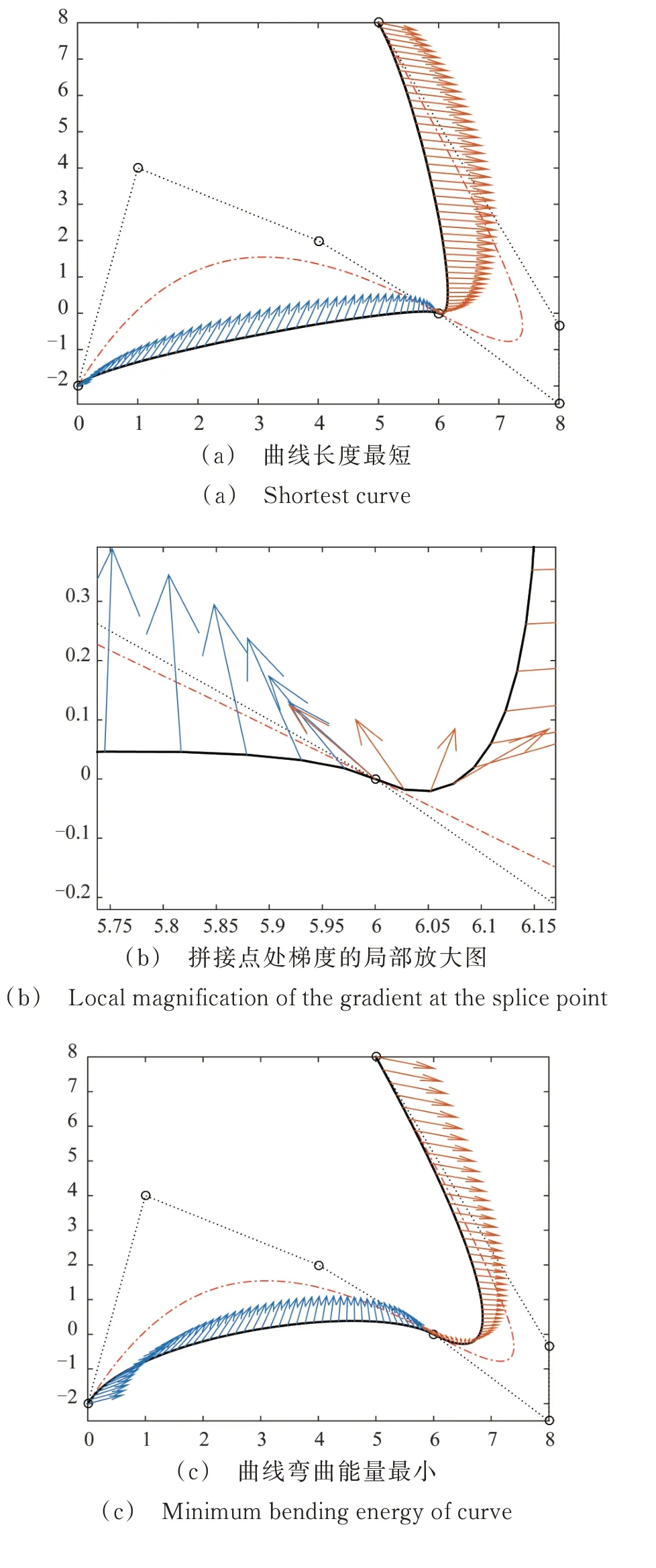
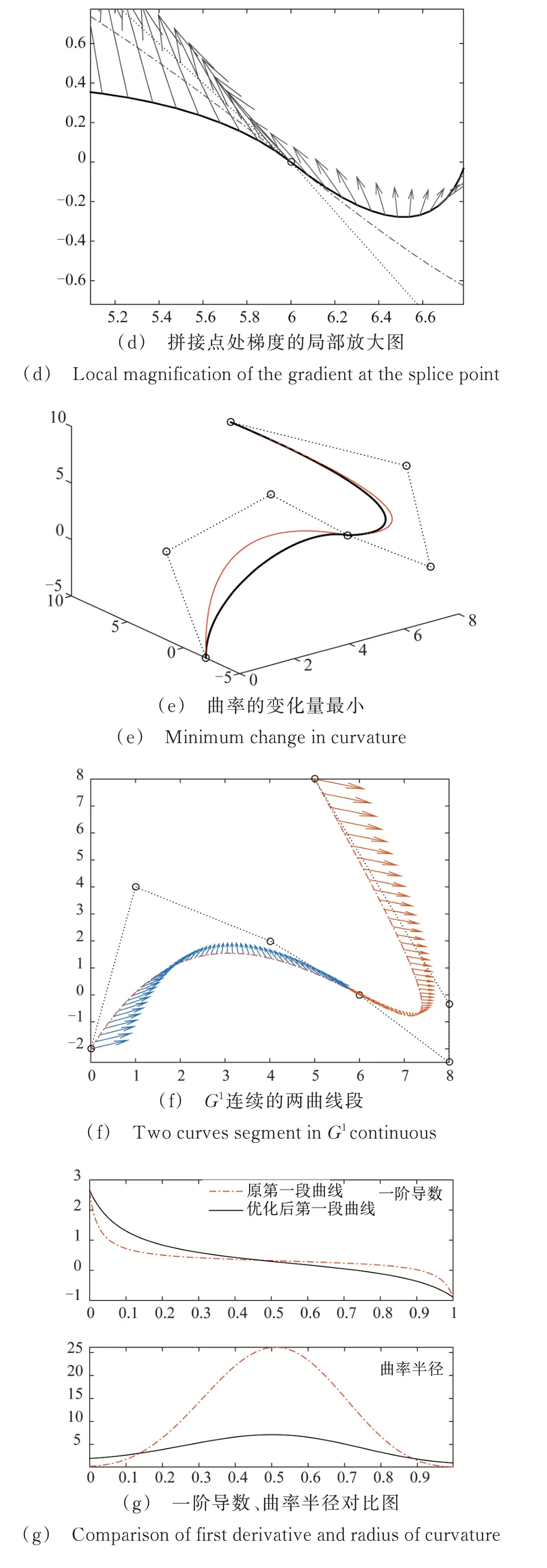
图9 3 种形状参数的选择Fig.9 Three selections of shape parameter
以2 段满足G1连续的三次α-DP 曲线为例,未优化的曲线见图9(f),此时目标函数可简化为
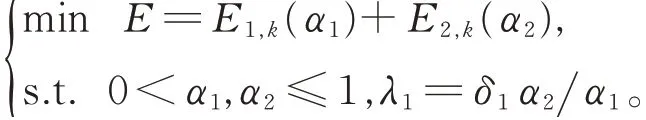
当k=1 时,计算可得α1=0.129 1,α2=0.242 0,此时2 段拼接曲线长度最短,见图9(a);当k=2 时,计算可得α1=0.371 6,α2=0.696 8,此时2 段拼接曲线弯曲能量最小,见图9(c);当k=3 时,计算可得α1=0.489 6,α2=0.918 0,此时2 段拼接曲线曲率变化量最小,见图9(e)。
图9(a)和(c)中,带箭头的线为曲线的梯度,图9(b)和(d)是2 段曲线在拼接点处的梯度的局部放大图。可以看出,2 段曲线优化后仍满足G1连续。(g)为原G1连续的第1 段曲线与优化后的第1 段曲线的一阶导数、曲率半径对比图。可以看出,当k=1 时,2 段曲线的一阶导数图比k=2 时2 段曲线的一阶导数平稳,说明当k=1 时曲线的变化率最小,曲线长度最短。而当k=2 时2 段曲线的曲率半径远小于k=1 时,说明当k=2 时曲线有最小的弯曲能量。
5 结 语
提出了一类带有形状参数的三次α-DP 基,形状参数α 为三次α-DP 曲线提供了独立于其控制顶点外的自由度,使其不仅继承了传统三次DP 基函数的优良性质,而且具有形状可调性。在光滑拼接方面,三次α-DP 曲线也达到了很好的效果:当满足一定条件时,相邻两曲线段间可以达到G2连续。讨论了形状参数α 具有的几何意义:当形状参数增大时(在取值范围内),三次α-DP 曲线逐渐逼近其控制多边形。此外,针对曲线的拉伸、弯曲以及扭曲能量,给出了3 种形状参数的选取方案以及相关数值实例。但本文未继续讨论任意次DP 曲线、圆或弧的精确表示以及α-DP 曲线与曲面在实际工程中的应用,有待下一步继续研究。
