虚拟震源测深法及其在INDEPTH-3 台阵中的应用

江洋

（浙江大学海洋学院，浙江舟山316000）

20 世纪90 年代，接收函数[1]对理解地壳结构起了重要作用。但在接收函数中最常用的PS 波和它相关的多重反射仅仅是有用信息的一小部分。与此同时，一种新而可靠的估计地壳厚度的方法——虚拟震源测深法(VDSS)，逐渐显现其优势。最初，为减少震源附近的散射对准确辨别Ss波和SsPmp 波的影响，虚拟震源测深法可以被利用的仅为深源地震，但在单个台站[2-5]和密集台阵[6-7]上都有很好的应用。近年来，YU 等[8]利用质点运动，将地震记录分解为P 类型和S 类型波，从而可以利用反卷积去除震源附近的散射,这种方法将可以利用的地震范围从稀有的深源地震拓展到经常发生的浅源地震。因此可以利用虚拟震源测深法，得到准确的地震剖面。此剖面有助于更直观地了解青藏高原下地壳的起伏变化情况，对研究青藏高原的地质演化具有重要意义。

1 研究方法和数据

1.1 虚拟震源测深法简介

虚拟震源测深法主要依靠Ss波与SsPmp 波的到时差来估算地壳厚度。假设地壳为单层的水平均一结构(见图1)，可以看出，Ss波与SsPmp 波传播时间的差值，主要取决于P 波在地壳中的传播时间，且地壳厚度与Ss波和SsPmp 波到时差值成正比。通过地震学里的Tau-p 理论，可以推得地壳厚度与Ss波和SsPmp 到时差值的数学表达式:

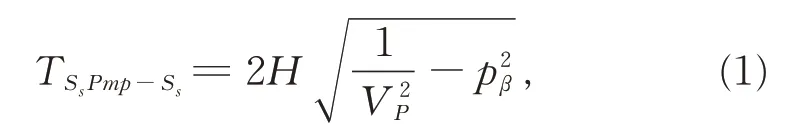
式(1)中，pβ为入射S 波的射线参数(水平方向慢度)，H 为地壳厚度，VP为地壳中P 波传播的平均速度。

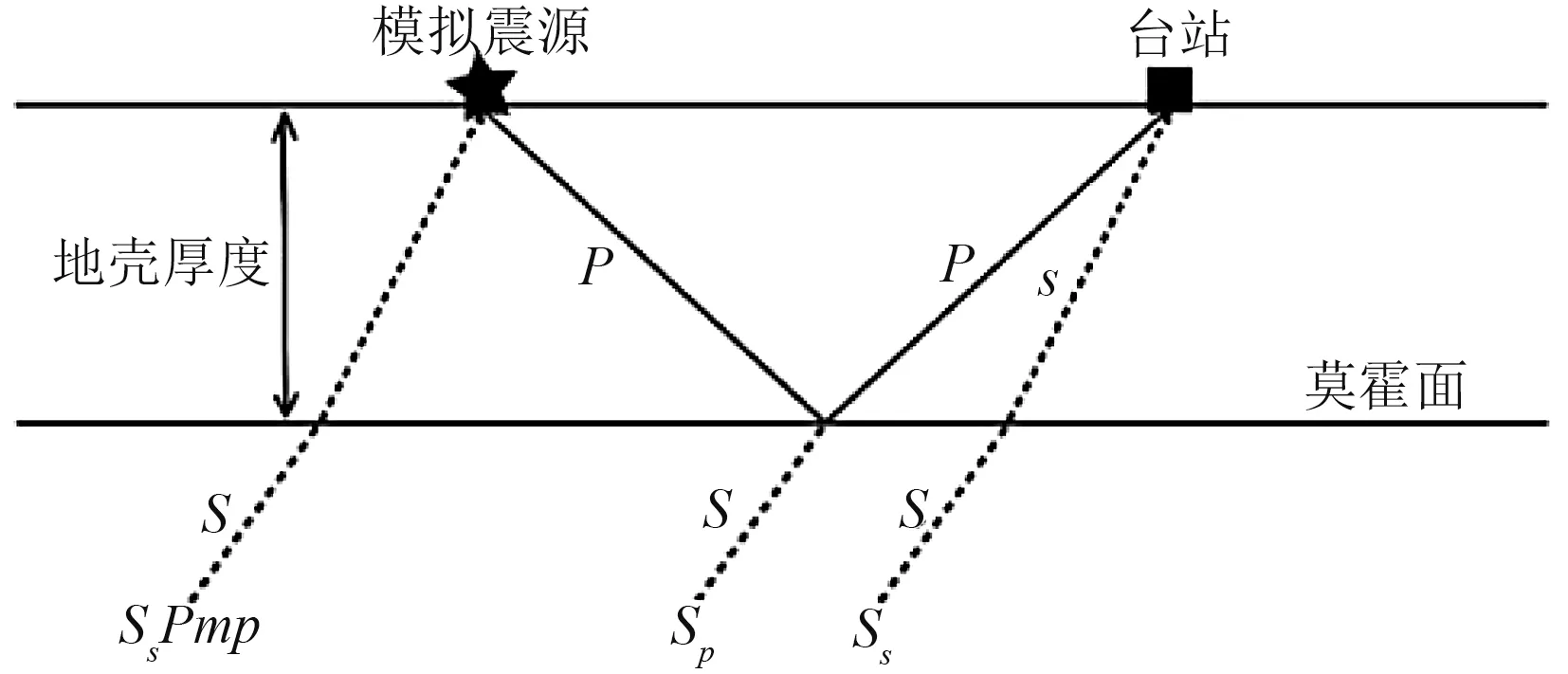
图1 Ss波和SsPmp 波在地壳和上地幔中的传播路径Fig.1 Ray-paths of Ss and SsPmp in the crust and uppermost mantle

从式(1)中可以看出，只需测出Ss波与SsPmp 波到时差，便可得到地壳厚度。但当震中距在30～55度时，SsPmp 波会在莫霍面顶部发生全发射，导致SsPmp 震相产生大约π/2 相移，因此，直接测量SsPmp 与Ss震相之间的到时差很困难。本文通过对观测地震记录的拟合来确定到时差，从而得到地壳的厚度。

首先建立一组单层地壳模型，如图2 所示，其中每个模型设定地壳中P 波的平均速度为6.3 km·s－1，S 波的平均速度为3.6 km·s－1，地壳平均密度为2.8 g·cm－3，泊松比为0.257 6。同时地幔中P波的平均速度为8.1 km·s－1，S 波的平均速度为4.6 km·s－1，地 幔 平 均 密 度 为3.3 g·cm－3，泊 松 比 为0.262 0。入射S 波的射线参数由台站和震源的相对位置计算得到。这些参数在每个模型中都是相同的，唯一不同的是地壳厚度。由式(1)，地壳厚度与到时差成正比，因此每个模型中的地壳厚度都对应一个到时差。因为地壳内部结构对于波形的拟合影响很小[9]，单层地壳模型就已足够。

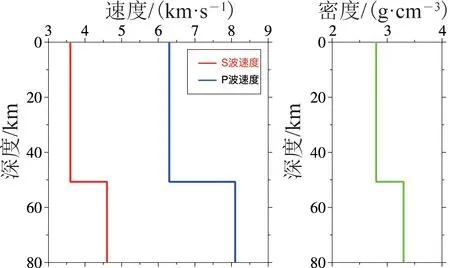
图2 单层地壳模型Fig.2 One-layer crustal model

其次,为了将地壳的结构响应与观测到的地震记录做对比,还需将结构响应与入射S 波进行卷积。为得到入射的S 波,先将同一地震台站数组中每个台站的P 波叠加，以减少噪声影响，得到相应的入射P 波。然后，利用P 波与S 波之间的衰减因子差Δt*(Δt*取决于地震的震源深度)，卷积后得到入射S 波。结构响应和入射S 波卷积的结果即为合成地震记录。

针对每一个台站及其对应的震源，按照不同的地壳厚度，建立一组合成地震记录，并计算观测到的地震记录和每个合成地震记录之间差值的L2 范数。据此决定最接近观测值的地震合成记录，确定准确的观测值。根据测量到的时差，便可通过式(1)计算从虚拟震源到台站区域的地壳平均厚度。

本文所用地震资料来自1998―1999 年中美合作项目INDEPTH-3(International Deep Profiling of Tibet and the Himalaya)在青藏高原布设的宽频地震仪所记录的地震波形数据。地震台阵全长约400 km，共49 个地震台站，如图3 所示。对于选取的地震记录，首先须去除仪器响应。为去除噪声的影响，本文在对观测地震记录和合成地震记录拟合过程中，均做了频率为0.05～0.5 Hz 的双通Butterworth滤波。

图4 是ST31 台站(图3 中红色三角形)的径向波形拟合结果，可以得到Ss波与SsPmp 波的到时差为12.2 s，计算得到从台站到虚拟震源的平均地壳厚度为69 km。

1.2 地震资料筛选及来源

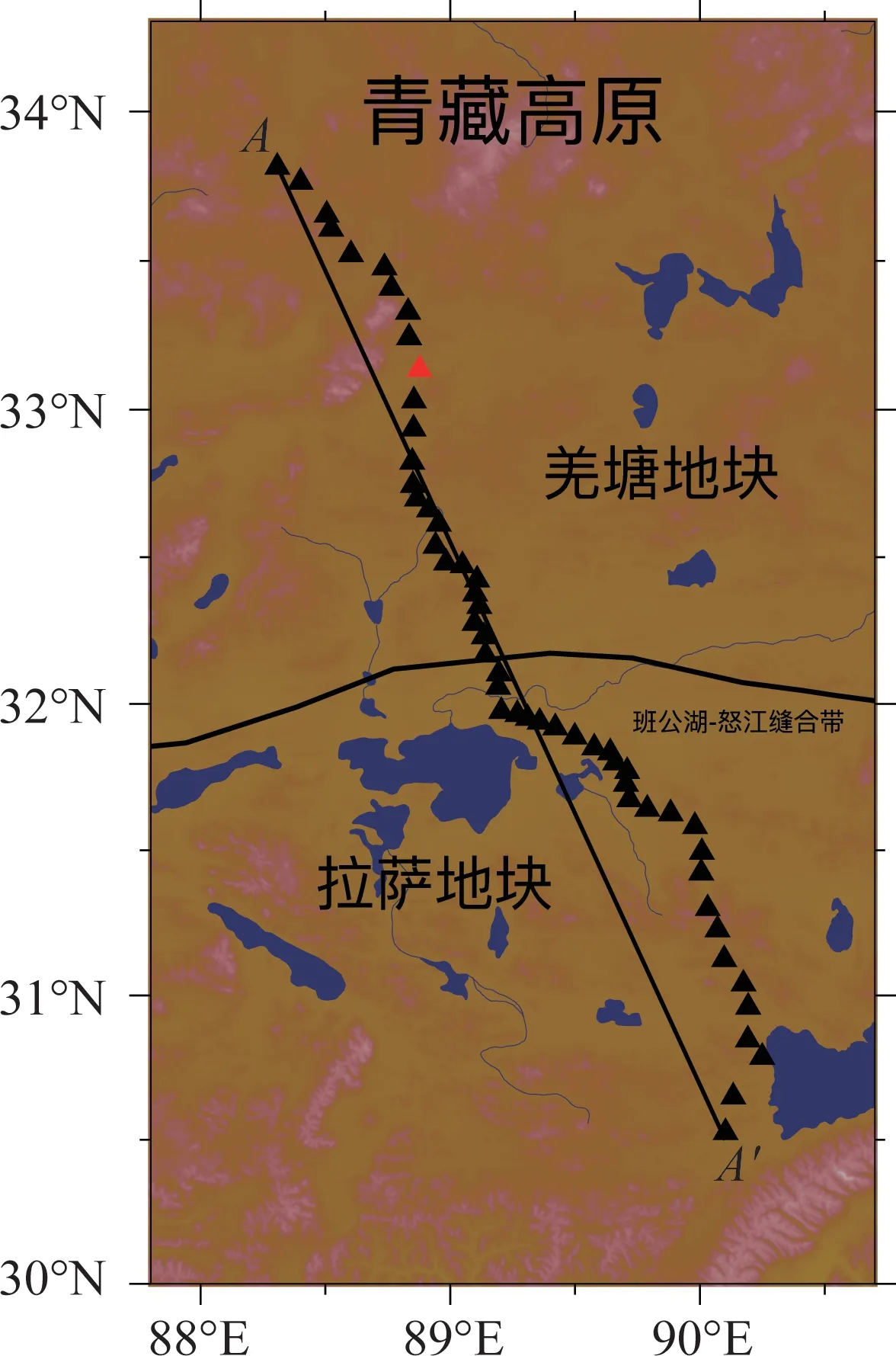
图3 INDEPTH-3 主台阵分布Fig.3 Map showing the locations of INDEPTH-3 main array

图4 台站ST31 径向分量波形拟合结果Fig.4 Radial component waveform modeling at station ST3

虚拟震源测深法对地震数据资料有很高的要求，一般情况下，必须满足条件:（1）Ss波足够清晰简单，这也要求震源的破裂过程简单，通常需深源地震。本文基于前人方法，但对数据的筛选不局限于少数深源地震，很多浅源地震同样可以选用。（2）SsPmp 波足够清晰，因此震中距范围选择在30°～50°，前者是为避免地幔转换带速度不连续引起的三叉震相影响，后者是为确保SsPmp 波能在莫霍面顶部发生全反射。（3）地震的体波震级应大于5.0 级，以确保信号-噪声的比例足够大。青藏高原地处环太平洋地震带和地中海-喜马拉雅地震带的交汇处，各个方向都有满足以上3 个条件的地震。

本文选取沿着INDEPTH-3 主线(A′-A)的虚拟地震剖面进行研究，从南到北剖面依次穿过拉萨(Lhasa Terrane)、羌塘地块(Qiangtang Terrane)，两地块之间以班公湖-怒江缝合带(BNS)为界，便于对比分析不同构造区域地壳厚度的差异。

2 计算结果

图5 展示的是沿INDEPTH-3 台阵的虚拟震源剖面(A′-A)，所建剖面的事件发生在1999 年3 月18日17∶55∶43(GMT)，地理坐标（142.97°E，41.10°N），震源深度41 km，震级5.9 (地震事件的信息来源于美国地质调查局(USGS)地震目录)。从图5 中可以看出：（1）从南到北(A′-A)，地面高程从4.7 km 逐渐变高到5.2 km，总体呈变高趋势，但变化幅度很小，仅为0.5 km。（2）虚拟地震剖面的Ss波和SsPmp 波清晰可见，同时，所含地震台站较多，剖面的可靠性很高。班公湖-怒江缝合带以南，地壳厚度基本保持在55～60 km，这部分结果与文献[10]中接收函数得到的结果比较吻合，但从班公湖-怒江缝合带向北，地壳厚度逐渐增加到75 km 左右。

3 讨 论

3.1 误差分析

在拟合观测地震记录时，假设地壳中P 波的平均速度为6.3 km·s-1，这在青藏高原是一个非常合理的预测，如果P 波平均速度有±0.3 km·s-1的变化，相应的地壳厚度仅有不到200 m 的变化[11]。这是因为根据式(1)，H 和VP存在此消彼长的关系，在拟合过程中，对到时差的预测也会有±0.2 s 的误差，带来1 km 的地壳厚度计算误差。

3.2 地球动力学解释

虚拟震源测深法和艾里均衡模型计算得到的结果如图5(c)所示，可以看出，从班公湖-怒江缝合带向南，虚拟震源测深法得到的地壳厚度为55～60 km，艾里均衡模型得到的地壳厚度为57 km，这两种方法得到的地壳厚度基本一致，说明班公湖-怒江缝合带以南的拉萨地块地壳达到均衡状态，地壳结构比较简单。

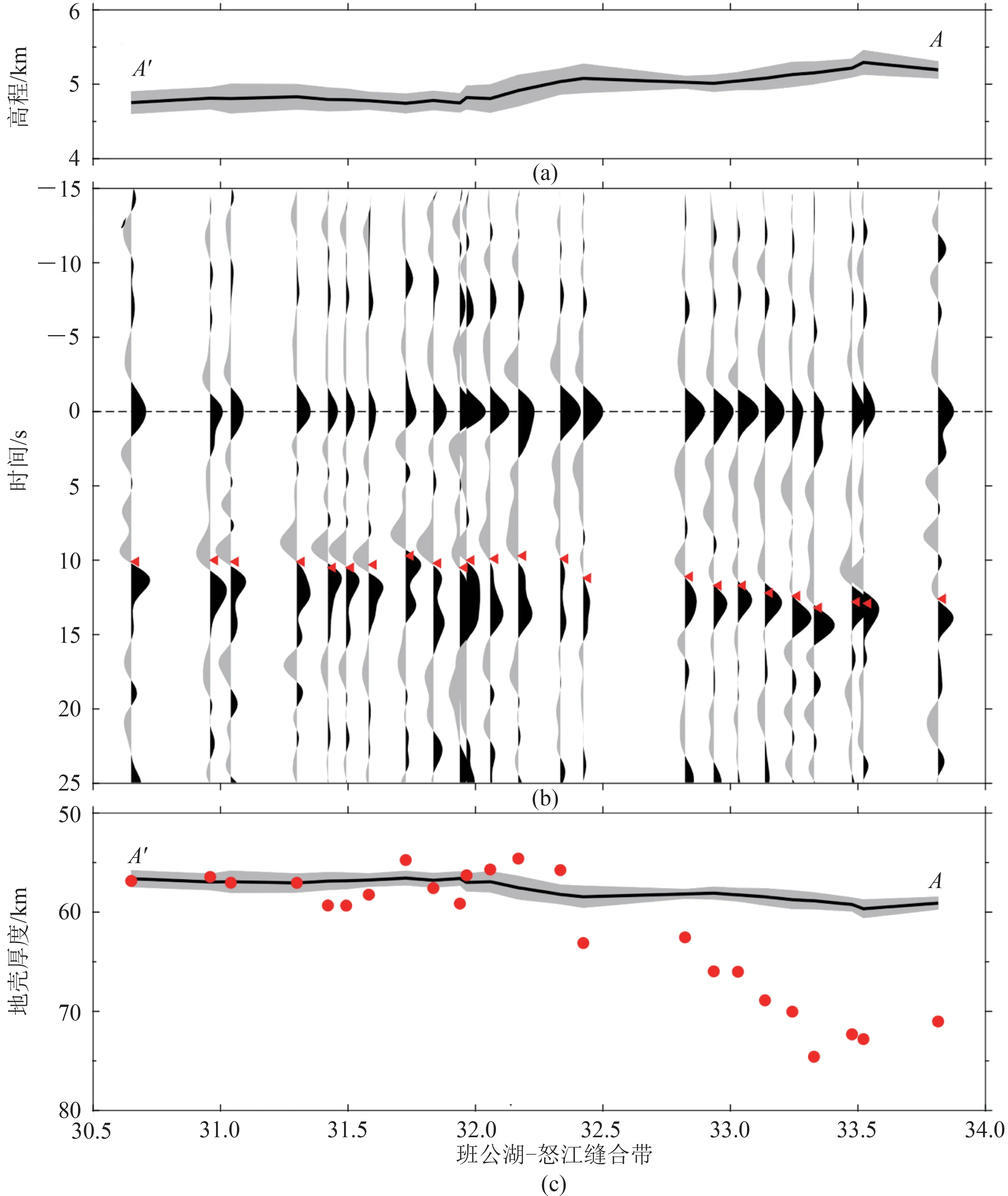
图5 INDEPTH-3 主台阵虚拟地震剖面Fig.5 Virtual seismic profile along INDEPTH-3

从班公湖-怒江缝合带向北，虚拟震源测深法测得的地壳厚度为60～75 km，艾里均衡模型得到的地壳厚度约为60 km，虚拟震源测深法计算得到的地壳厚度明显比艾里均衡模型得到的要厚。要支撑羌塘地块5 km 多的高程，有3 种可能。第1，本文可能低估了Ss波与SsPmp 波在上地幔中传播路径差对的影响，也就是说拉萨地块与羌塘地块下上地幔的S 波速度存在明显的侧向差异，但由于缺乏INDEPTH-3 主线附近区域可靠的层析成像结果，很难确认这种可能性的大小；第2，羌塘地体下存在高温流体，密度低，从而支撑起羌塘地块；第3，MEISSNER 等[12]的 研 究 发 现，INDEPTH-3 台 阵 北端，羌塘地块的下地壳和地幔存在低速体且壳幔边界复杂，这可能会导致SsPmp 和Ss波到时差变大，从而使虚拟震源测深法计算得到的地壳厚度变大。第4，由于印度板块的碰撞，导致羌塘地体的岩石圈发生形变，呈先向上、再向下俯冲的趋势，这种可能性也与地球动力学相符。同时此结果与赵文津等[13]通过层析速度结构剖面得到的印度大陆地幔岩石圈在北纬32°以较大角度向北俯冲的结果一致。

4 结 论

利用虚拟震源测深法，对青藏高原中部地壳和上地幔结构进行了初步研究，结果显示，拉萨地体和羌塘地体下的地壳结构差异显著，拉萨地体的地壳厚度为55～60 km，与艾里均衡模型得到的结果一致，而羌塘地体的地壳厚度为60～75 km，整体向北增厚，比艾里均衡说预测的地壳厚度要厚得多。笔者认为，造成羌塘地体地壳厚度比艾里均衡预测厚的原因与羌塘地体下存在高温流体和低速带，或者与印度大陆地幔岩石圈在班公湖-怒江缝合带以北向下俯冲有关。