鱼雷锚在钙质砂床中的贯入深度研究

2020-04-21王呈陈晓辉喻国良

浙江大学学报（理学版） 2020年2期

王呈，陈晓辉，喻国良*

（1.上海交通大学船舶海洋与建筑工程学院海洋工程国家重点实验室, 上海200240； 2.上海交通大学高新船舶与深海开发装备协同创新中心，上海200240）

0 引言

目前, 海洋资源的开采已进入3 000 m 的超深水领域[1]。海洋浮式结构，如海上钻井平台、浮式生产储油卸油装置等，是海洋资源开采必不可少的设施。系泊系统作为海洋浮式结构的重要组成部分,随着海洋结构物规模及水深的增加, 其建造成本及施工难度也大幅提高。因此, 快速施工、降低成本、安装简便、高可靠性成为当今系泊系统的发展趋势[2]。相对于传统锚固结构，鱼雷锚安装简单快速，制造成本低，是一种有前景的深海锚固结构[3]。鱼雷锚由巴西石油公司于1996 年首次提出，并于2001年12 月成功应用于大型浮式生产储油卸油装置[3-4]。在实际应用中，首先将鱼雷锚从一定高度的海床上释放，随后在自重作用下在水体中不断加速并最终高速贯入海床[3]。在黏性海床中，其贯入深度可达锚长的2～3 倍[5-6]，在钙质砂床中的贯入深度尚待探明。由于鱼雷锚的抗拔力与贯入深度、海床特性等有关[7-9]，因此，研究鱼雷锚在钙质砂床中的贯入深度对鱼雷锚的工程应用具有实际意义。

当前，国内外对于鱼雷锚在钙质砂床中贯入过程的研究十分有限。RICHARDSON[5]曾通过室内实验观测了不同贯入速度下(23.4～29.4 m·s-1)鱼雷锚在砂土中的贯入深度。ZHANG 等[10]采用离散有限元（DEM）算法研究了鱼雷锚在砂土中的贯入过程，但未建立鱼雷锚在钙质砂床中贯入深度的预测公式。而且，采用离散有限元法时，鱼雷锚和土体均被粒子化，仿真耗时较长。至今，对于影响鱼雷锚在砂土中贯入深度的因素等尚缺乏系统研究，且缺乏快速准确预测鱼雷锚在钙质砂床中贯入深度的公式。

为此，本文将耦合的SPH-FEM 算法引入鱼雷锚在钙质砂床中的贯入深度研究，利用数值模拟方法研究贯入速度(0～45 m·s-1)、锚重和摩擦系数等对贯入过程的影响，基于能量法提出了鱼雷锚在钙质砂床中贯入深度的预测公式，为鱼雷锚在钙质砂床中的应用提供理论指导。

1 计算模型

1.1 鱼雷锚几何模型

以RICHARDSON 于2008 年使用的E0-1 型无鳍鱼雷锚为研究对象。此鱼雷锚可通过在锚体内添加废金属来增加鱼雷锚的贯入深度[1,11]。考虑到锚重的影响，在不改变锚体几何参数的条件下，选配了5 种不同锚重(m)，分别为118.4 t (E0-1 锚)、114.4 t(IE0-1 锚）、90 t (E0-2 锚)、125 t (E0-3 锚)、140 t(E0-4 锚)。其投影面积Ap和侧表面积As分别为1.13 和48 m2。鱼雷锚有限元模型如图1 所示，其中，d 表示锚体直径，L 表示锚长，Ltip表示锚尖长度，Ls表示除锚尖部分的锚体长度。考虑到所研究问题的空间对称性，为缩短计算时间，锚体和土体均选用1/4 的结构。由于锚体在运动过程中通常不会发生变形，故设为拉格朗日刚体。

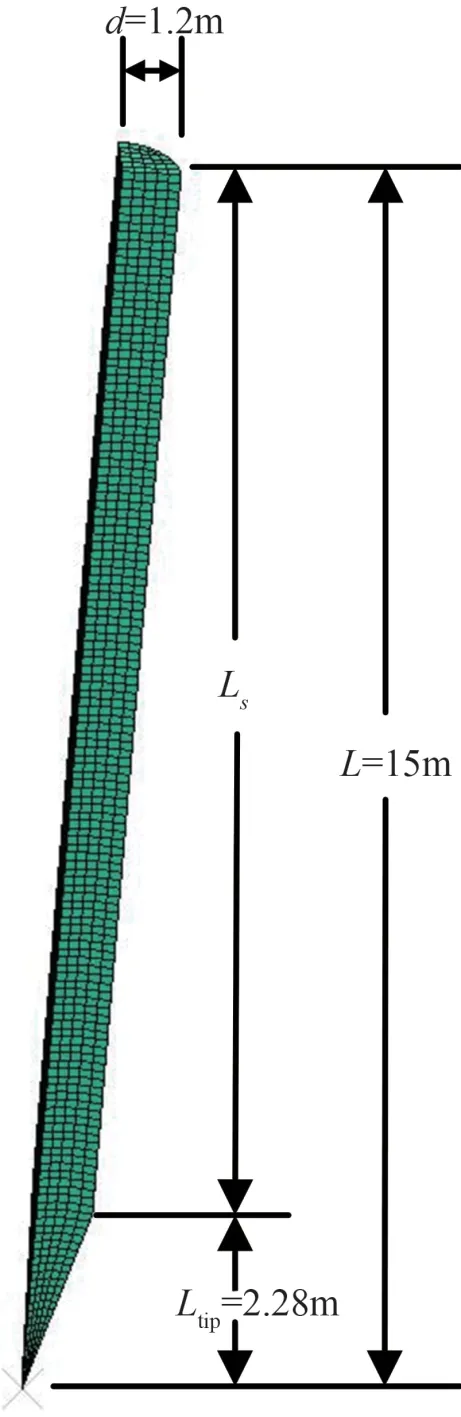
图1 鱼雷锚有限元模型Fig.1 Finite element model of torpedo anchor

1.2 土体几何模型

采用SPH 方法对锚体周围的局部土体进行有限元模拟。鱼雷锚在贯入过程中，锚体周围的土体会出现大变形，离锚体越远的区域土体变形越小。若采用通用的Lagrangian 方法计算，锚体周围的土体网格会发生严重扭曲，导致计算发散。SPH 方法作为一种无网格Lagrangian 粒子法, 粒子之间不需要网格进行连接，其计算精度不会受物质变形的影响, 可用来求解大变形问题，且其计算速度往往比CEL 方法快[12]。SPH 方法使用各种插值技术，建立区域中待求粒子与周围任意粒子的关系，待求粒子上的变量值可通过一组相邻粒子贡献的和来近似，即

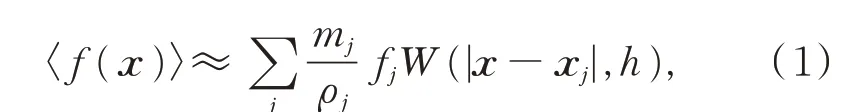
其中，〈f (x)〉为粒子变量f(x)的近似值，m 为粒子质量，ρ 为粒子密度，x 为位置矢量，下标j 表示周围粒子编号，h 表示光滑长度，W 表示“核”函数或光滑函数（见图2）。

为避免土体边界对鱼雷锚贯入过程模拟的影响，土体的几何尺寸取为20 d×20 d×5.5 L（长×宽×高）。由于SPH 算法的计算时间比传统的Lagrangian 算法长，为减少计算时间，仅锚体附近大变形区域的土体采用均匀的SPH 粒子模拟，其他区域仍采用传统的Lagrangian 网格模拟。土体三维有限元模型如图3 所示。为保证计算精度、缩短计算时间，参考已有的研究，SPH 粒子区域尺寸取为7 d×7 d×3 L，SPH 粒子直径为0.24 m[10,12-13]，粒子总数为470 492。砂土选用摩尔库伦本构模型，泊松比取0.2[14]，弹性模量取10 MPa，土体的剪胀角取ψ=Φ－30°[15]。为避免数值发散，赋予土体一个很小的黏聚力200 Pa[15]。砂土的特性参数可参考RICHARDSON[5]的实验数据，具体见表1。

图3 土体的三维有限元模型Fig.3 Three-dimensional finite element model of soilution around anchor

表1 海床的土体特性Table 1 Soil properties of seabed［5］

1.3 边界条件设置

由于施工企业的项目有着分布广的特性，为此持续的财务监督是必不可少的。通过将综合检查和专项检查相结合，自查和互查相结合，从而形成全方位覆盖的监督监察网，保证施工企业工程项目部的财务管理有效性、防止成本失控与效益的流失。要将检查作为日常检查制度，实行业务考核制度，有效提高制度的执行力，提高员工的工作积极性。

锚体与SPH 粒子间采用基于节点与面的通用接触，其切向接触特性为基于罚函数的摩擦过程。考虑锚土界面摩擦系数(μ)对贯入深度的影响，分别选取0.2，0.25，0.31，0.4 四种不同的摩擦系数值[10]。SPH 粒子与相邻的Lagrangian 网格土体之间采用Tie 约束。此外，在土体的竖直边界施加水平方向的速度约束，在土体下底面施加竖直方向的速度约束。锚体以指定的初始贯入速度Vi垂直地贯入海床。具体的模拟工况如表2 所示。

表2 模拟工况Table 2 Simulated case

2 数值结果分析

2.1 数值验证

针对RICHARDSON[5]的实验，采用耦合的SPH-FEM 方法模拟了鱼雷锚在砂床中的贯入过程。如表3 和图4 所示，耦合的SPH-FEM 方法计算得到的鱼雷锚贯入深度与实验值基本一致。例如，对于25 m·s-1的初始贯入速度，实测贯入深度为22.4 m，耦合SPH-FEM 的计算值为23.39 m，计算相对误差为4.42%。由此可见，耦合的SPH-FEM方法可准确评估鱼雷锚在砂床中的动态贯入深度。

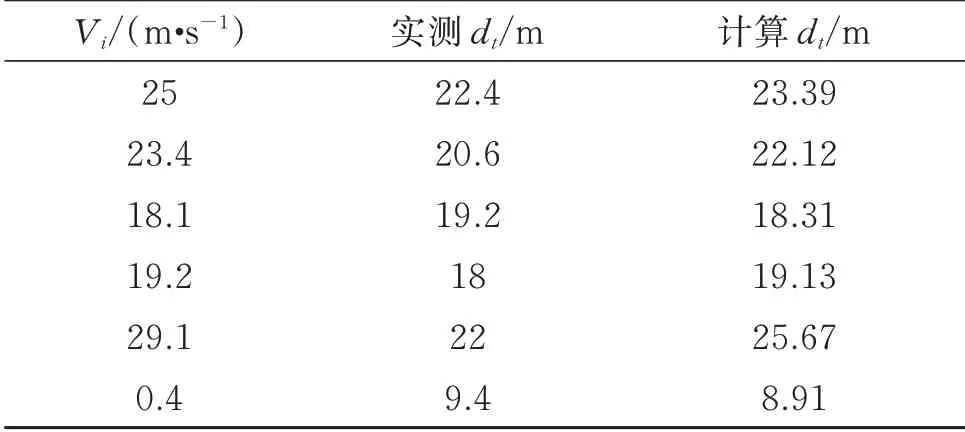
表3 数值模型验证Table 3 Validation of numerical model

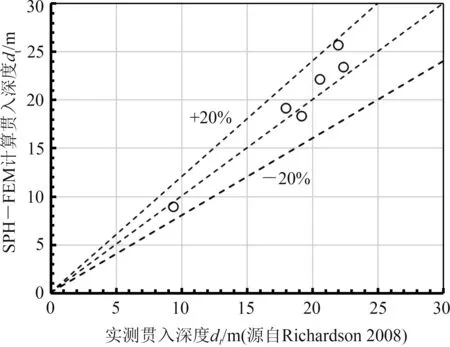
图4 实测贯入深度与数值仿真结果对比Fig.4 Comparisons between the measured penetration depth and the numerical simulation results

2.2 贯入过程中的土体移动特性

鱼雷锚在砂床中下落时，锚体受到的作用力分别是：锚体自身浮重力(Ws)、锚体底部的端承阻力(Fb)、锚体侧面摩擦阻力(Fs)和惯性阻力(Fd)。根据模拟结果，鱼雷锚在钙质砂床中的贯入过程可分为如图5 所示的4 个阶段：（1）初始阶段（t ≤0.08 s），鱼雷锚快速贯入土体。锚尖处的土体开始发生破坏，锚尖周围砂面略微向上隆起。锚体惯性阻力和底部端承阻力逐渐增大。锚重力大于阻力，鱼雷锚速度逐渐增加。（2）随后（0.08 s＜t ≤0.85 s），鱼雷锚形成空腔。锚杆逐渐贯入土体，土体的破坏方向由锚尖区域逐渐向锚杆周围发展，锚杆周围土体朝背离锚尖方向运动。在此阶段，侧面摩擦阻力对锚体阻碍作用越加明显，惯性阻力逐渐减小，锚重力小于锚体所受阻力，鱼雷锚开始减速。（3）接着（0.85 s＜t ≤1.4 s），鱼雷锚全部贯入砂床，其后方土体被排开且不会发生回流，进而形成空腔。（4）最后阶段（1.4 s＜t≤1.7 s），鱼雷锚速度迅速减小到0，锚体贯入过程结束。锚体周围破坏的土体逐渐恢复至静止状态。此阶段，惯性阻力减小为0，锚体重力与端承阻力和侧面摩擦阻力到达平衡。

2.3 贯入速度的影响

数值结果表明，贯入速度对鱼雷锚的贯入深度有很大的影响。如图6 所示，鱼雷锚的贯入深度随贯入速度的增大而增深。鱼雷锚初始释放高度越高，所获得的贯入速度越大，即贯入动能越大，贯入深度越深。以E0-1 锚为例，当贯入速度较小时（如图6 中速度小于6 m·s-1），贯入深度随贯入速度的增大缓慢增加，随后，当速度超过某个值后，贯入深度随贯入速度的增大呈近似线性增加趋势。对此线性增长区域的数据采用线性拟合分析，得到贯入深度与贯入速度的关系：dt= 0.638 Vi+ 6.887，线性相关系数R2= 0.99。此外，在相同速度下（23.4～29.1 m·s-1），鱼雷锚在砂床中的贯入深度与锚长的比值为1.33～1.93，明显低于RICHARDSON[5]给出的鱼雷锚在软黏土中的贯入深度与锚长的比值（2.53～2.8）。这主要是由于钙质砂床中的端面阻力系数（约32[5]）和摩擦角（约40°[5]）比软黏土中的端面阻力系数（约12[5]）和摩擦角（约23°[5]）大，导致钙质砂床中鱼雷锚贯入所受的端面阻力和侧面摩擦阻力比软黏土中的阻力大，使得鱼雷锚在钙质砂床中的贯入深度较软黏土中的深度小。总之，有必要提高鱼雷锚在水体中的下落高度来获得更高的初始贯入速度，进而获得理想的贯入深度。

图5 钙质砂床土体移动特性Fig.5 Soil movement characteristics of calcareous sandy bed

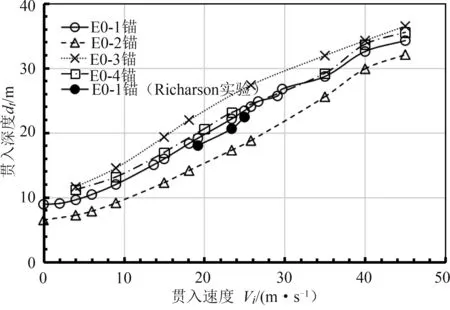
图6 贯入速度对鱼雷锚贯入深度的影响Fig.6 Effect of impact velocity on penetration depth of torpedo anchor

2.4 锚重的影响

数值结果表明，锚重也是影响鱼雷锚贯入深度的一个重要的因素。从能量观点分析，鱼雷锚的贯入初始动能，与锚重成线性关系，即锚越重，初始动能越大，贯入深度亦越大。从受力分析看，由牛顿第二定律，鱼雷锚运动过程中的合力等于锚重减去鱼雷锚所受的阻力。锚越重，贯入速度减小越慢，贯入深度越深。图7 给出了4 种不同重量的鱼雷锚贯入深度随贯入速度的变化曲线。由图7 可知，当锚重从90 t 增重为140 t 时，鱼雷锚贯入深度可从12.25 m 增加到19.23 m，增加了56.98%。此外，当鱼雷锚贯入速度接近于0 时，锚重对贯入深度有显著影响。如图6 所示，对于E0-1 锚，在0 m·s-1下的贯入深度为8.91 m，此时锚重比贯入速度对贯入深度的影响更大。在实际工程中，往往通过在锚体内添加金属填充物等来增加锚重以提高鱼雷锚贯入深度。

图7 锚重对鱼雷锚贯入深度的影响Fig.7 Effect of anchor weight on penetration depth of torpedo anchor

数值结果表明，锚-土间摩擦系数通过改变鱼雷锚所受的侧摩阻力间接影响其贯入深度。本文模拟了4 种摩擦系数值下鱼雷锚的贯入过程。图8 显示了4 种摩擦系数值下鱼雷锚贯入过程中的速度-位移轮廓图。模拟结果表明，锚-土间摩擦系数越大，鱼雷锚速度越小，锚体贯入深度越浅。由RICHARDSON[5]提出的桩在砂土中的摩擦力公式可知，摩擦力与摩擦系数成正比，即摩擦系数越大，摩擦阻力越大，鱼雷锚贯入深度也就越小。当摩擦系数从0.2 变为0.4 时，鱼雷锚贯入深度从16.46 m降为14.49 m，减小了11.97%。

图8 摩擦系数对鱼雷锚贯入深度的影响Fig.8 Effect of friction coefficient on penetration depth of torpedo anchor

3 鱼雷锚在钙质砂床中贯入深度的预测公式

3.1 基于能量法的鱼雷锚贯入深度计算

鉴于鱼雷锚在贯入过程中的总能量守恒，即贯入动能和重力势能转化为内能，可以对O'LOUGHLIN 等[16]提出的鱼雷锚在黏性土体中贯入深度的能量法进行修正，得到鱼雷锚在砂床中贯入深度的能量法公式：

其中，Etotal表示总的机械能，γ′表示土体的有效重度，deff表示鱼雷锚的等效直径，对于无鳍鱼雷锚，deff=d，g 表示重力加速度，p 和q 表示无量纲的拟合常数。

重新整合式（2）和（3），得到最终的能量法预测公式：

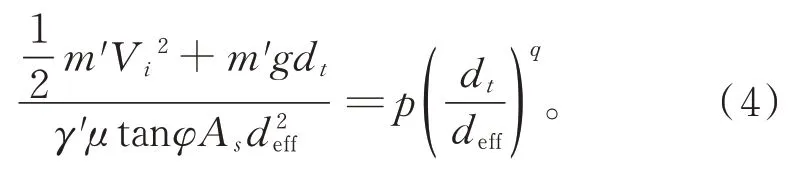
需要特别注意的是，此式在使用时需进行几次尝试性抛锚实验并结合非线性分析来确定p 和q 的值。对于其他工况，在已知p 和q 的情况下，需编程求解此非线性方程（4）来获得贯入深度。结合本文仿真数据以及非线性拟合分析，计算求得鱼雷锚的p =0.78，q = 0.47。图9 展示了能量法的拟合效果。结果表明，所有的数据点均紧密地落在拟合线两侧，拟合公式的相关系数R2= 0.98。此外，如图10 所示，能量法计算鱼雷锚的贯入深度与耦合的SPH-FEM数值模拟结果对比表明，约95.4% 的数据点都在±20%的相对误差范围内。可见，式（4）可准确地评估鱼雷锚在砂床中的贯入深度，且形式和求解过程简单。

图9 能量法拟合Fig.9 Fitting of energy method

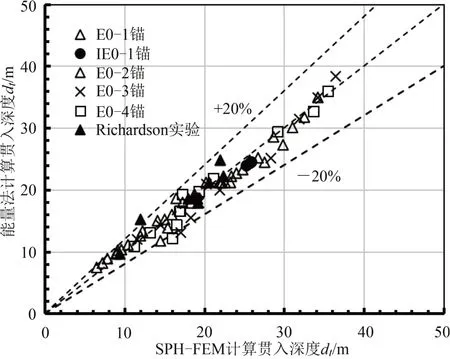
图10 能量法计算的贯入深度与数值模拟结果对比Fig.10 Comparison of penetration depth of torpedo anchor calculated by energy method with numerical simulated results

在工程中使用时，先通过3 组抛锚实验，确定式(4)中的拟合系数p 和q；接着，通过Matlab 编程或Excel 求解式(4)，获得其他工况（不同贯入速度、锚尺寸和摩擦系数）下的贯入深度。

3.2 能量法的扩展应用

理论上，上述基于能量法的贯入深度计算公式（4）也适用于DPAⅢ动力贯入锚，只是其参数p、q 需重新确定。利用CHOW 等[17]的DPAⅢ动力贯入锚实验数据，通过数据拟合得到p = 1.53，q = 0.37。图11 展示了能量法预测DPAⅢ动力贯入锚的贯入深度与实验贯入深度的对比，预测的数据中有84.6%的点落在±20%的相对误差范围内，同时所有的数据点均位于±30%的相对误差范围内。可见，能量法也可准确地预测DPAⅢ动力贯入锚在砂床中的贯入深度。