微生物胶结砂体巴西劈裂试验声发射特性的细观模拟

陈春锦， 徐国宾， 唐 阳， 段 宇

(天津大学 水利工程仿真与安全国家重点实验室， 天津 300354)

1 研究背景

混凝土是水利工程建设中的主要建筑材料，但传统水泥的生产会造成一定的环境污染，微生物诱导方解石沉积(MICP)技术作为一种新型生物介导地基土改良技术，具有无污染、可持续、低耗能的特点，避免了采用化学方法进行地基加固和边坡防护时造成的土体化学污染问题[1]。

基于MICP技术获得的微生物胶结砂体(MCS)可用于岩土体的加固改良，已有的有关MCS材料的研究，少有涉及MCS材料的粘结特性或破裂过程，因此对于其细观变形特征和破裂过程尚不清晰，制约着MICP技术的进一步应用。巴西劈裂试验在岩石领域应用广泛，现也用于测量岩土的抗拉强度[2-3]。试验过程中岩土内部会产生声发射现象，基于这一现象可分析材料破裂过程及细观变形特征[4-6]，就目前研究现状来看，已有不少文献对巴西劈裂声发射事件开展研究[7-10]，但对MCS材料的声发射特性研究甚少。

本文引入地震学中发展而来的矩张量理论，基于典型试验工况下的胶结样本，从细观尺度模拟MCS在巴西劈裂过程中的破裂过程。研究成果为MCS破裂过程的研究提供了一种新的思路。

2 研究方法

2.1 材料颗粒流理论简介

颗粒流程序PFC是在细观离散单元法的基础上开发的一种通过球形颗粒运动与相互作用模拟固体力学和颗粒介质特性的有效工具[11]。

在PFC程序中，采用颗粒单元构建计算模型，颗粒间的粘结模型包括接触粘结和平行粘结。接触粘结模型能够传递法向压力、切向剪切力和法向拉力，但是无法传递力矩，当切向拉力或剪切力达到材料的拉伸强度或剪切强度时，接触粘结发生断裂。平行粘结的粘结面是一个有限面，可以传递力矩，当接触面上最大法向应力或剪切应力达到材料的拉伸强度或剪切强度时，接触粘结发生断裂[12]。

2.2 声发射信息提取

目前对于粘结键事件提取声发射信息主要有两类方法[13]：(1)根据断裂事件中释放的动能，计算声发射事件的量级；(2)断裂事件发生时周围颗粒间接触力会产生变化，据此计算声发射事件的矩张量。

由于大部分粘结键断裂时会释放出相似的能量数值，因此在PFC程序中，如果采用第1种方法来提取声发射信息，需要先解决如何将独立的断裂事件汇聚成一个声发射事件的问题。而对于第2种方法，由于在数值模型中可直接获取颗粒的受力及其产生的运动，故可由粘结破坏时周围颗粒接触力的变化计算得到矩张量。基于以上分析，本文采用计算声发射事件矩张量的方法来进行微生物胶结砂体结构裂纹演化规律分析。

2.3 声发射模拟参数确定

影响PFC中声发射模拟的主要物理量有品质因子Q和剪切波速VS，这两个参数可以通过以下公式得到：

(1)

(2)

式中：α为阻尼系数；E为弹性模量，Pa；ν为泊松比；ρ为密度，kg/m3。根据文献[14]中关于品质因子的探讨并结合MCS的材料特性，本文将品质因子Q设置为100，剪切波速通过计算求得。

2.4 矩张量与矩震级的求解

地震学中，矩张量是通过对震源边界或破坏源边界积分得到的。对于颗粒流模型，震源边界则是裂纹面。假定裂纹两端接触的颗粒为源颗粒，当粘结键发生断裂时，源颗粒必定会发生移动，接触力也随之变化。因此，矩张量即作用于源颗粒上的所有接触力力臂与其对应的变化量相乘之和，表达式为：

(3)

式中：ΔFi为第i个接触力；Rj为第j个接触点与裂纹中心距离。

声发射事件具有一定的持续时间，故矩张量的计算也是实时的，即事件持续时间内的每个时间步长均会计算矩张量。在PFC程序中，如果每一时间步长的矩张量都被计算并存储，则会占用很多内存。为避免这一问题，声发射事件的矩张量取具有最大标量力矩时的矩张量。标量力矩的表达式为：

(4)

式中：mj为矩张量的第j个分量。

声发射事件的矩震级Mw可由下式计算得到:

(5)

矩震级反映了断裂事件的破坏强度，表征了每次断裂事件所造成断裂面错动的大小以及其释放的能量[15]。

3 数值模型构建及细观参数选取

本试验菌种为巴氏芽孢杆菌(Sporosarcina pasteurii,美国国家菌种库编号ATCC11859)，是MICP技术应用中常用的一种菌种。微生物胶结砂体的具体试验方法在文献[16]中已有详细介绍，本文不再赘述。基于前期研究结果[16]，本文选取OD600=1.50，[Ca2+]=0.75 mol/L的砂柱样本作为研究对象，通过标定后的数值模型研究样本在巴西劈裂作用下的破裂特征，其中巴西劈裂的加载速率与室内试验相同，为0.05 mm/min。

Tang Yang等[17]的研究结果显示，MCS材料中砂颗粒与砂颗粒之间、砂颗粒与方解石之间以及方解石与方解石之间均存在粘结，这种粘结特征与PFC中的平行粘结模型较为接近。Feng Kai[18]采用线性平行粘结模型模拟了MCS的力学特性，其研究结果证明了模拟的合理性。因此，本文选定平行粘结模型来模拟砂颗粒与砂颗粒之间、方解石与方解石之间以及砂颗粒与方解石之间的粘结特性。基于Xu Guobin[16]等利用XRD分析胶结材料的物相组成结果可知，试验工况下的微生物矿化后主要成分为石英颗粒和方解石。对于石英颗粒，其形状多为圆形，且当前对于此粒径的石英颗粒已有研究者用圆形来模拟[19]。因此本文采用圆形来模拟砂颗粒；对于方解石颗粒，形状呈现不规则形态，不规则颗粒与圆形颗粒相比，其存在更多的物理接触[20]，且在材料[21]的力学行为中起着关键作用，因此方解石采用具有不规则形状的颗粒体Clump来模拟。最终建立的MCS巴西劈裂数学模型如图1所示。

在PFC程序中由于输入的细观参数与MCS结构的宏观参数并无直接对应的关系，因此，对于细观参数标定的通用方法为“试凑法”，目前一直被广泛应用[22-23]。前期研究[17]已经对石英-方解石数值模拟开展了细观参数的标定，如表1所示。考虑到微生物胶结砂体材料内部呈现非均匀性特征，颗粒间的粘结状况也会呈现出一定的差异，导致材料强度的不均匀性分布。为使数值模拟结果与宏观物理特性更为接近，借鉴Potyondy等[24]和Tang Yang等[25]针对此问题的处理方法，细观参数赋值时引入了Gauss分布，从而更好地体现了数值模型的离散性。将数值模拟得到的最终破坏形态与MCS物理试样的最终破坏形态相对比，如图2所示，数值模拟的试样破坏形态与实际破坏形态基本一致。证明了物理试验与数值模拟的一致性，同时说明对MCS细观参数的选取是合理的。

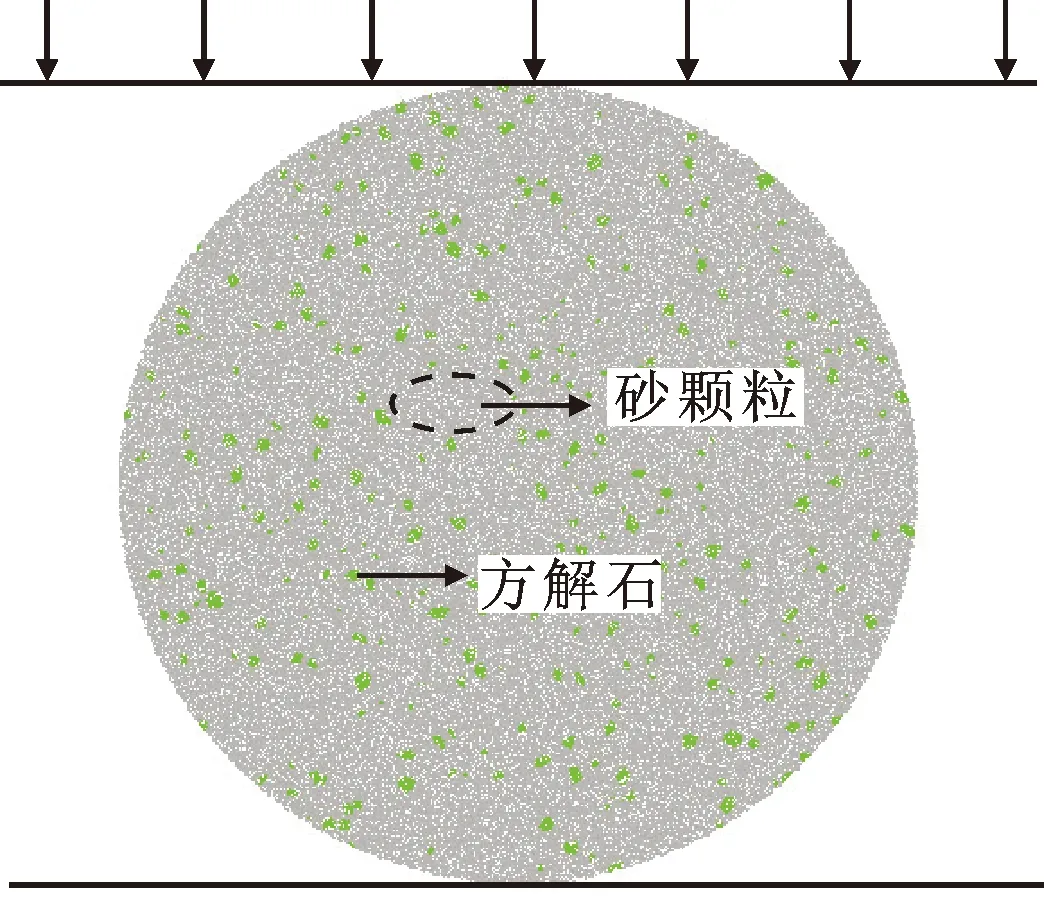
图1 微生物胶结砂体巴西劈裂数学模型示意图

表1 细观接触参数[17]

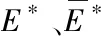
图2 数值模拟与实际破坏形态对比图

4 微生物胶结砂体破裂过程分析

图3为MCS在模拟巴西劈裂试验过程中的应力-应变曲线，其中点A、B、C、D、E、F对应的应变值分别为0.5‰、1.0‰、1.5‰、2.0‰、2.75‰和3.0‰。图4为不同应变下破裂强度的矩震级云图，结合图3和图4，分析微生物胶结砂体的破裂过程。

图3 微生物胶结砂体在模拟巴西劈裂试验过程中的应力-应变曲线

图3中OA段为密实阶段。加载初期试样内部空隙逐渐闭合，颗粒与颗粒在此阶段发生错动，产生微小裂纹。A点的矩震级云图(图4(a))显示，模型的顶部和底部开始产生破裂能量，声发射事件的破裂强度较低。

图3中AD段为弹性变形阶段。此阶段试样内部近似为弹性体，应力-应变曲线基本呈直线，试样呈线弹性发展趋势。由于内部微裂纹的缓慢闭合和颗粒之间的相互摩擦，裂纹逐渐扩展。从图4(c)可以看出,AD段试样顶部和底部的破裂能量沿中轴线逐渐向中间扩展，结构内部微裂纹缓慢增多，主要在材料的中轴线附近分布。

图4 不同应变下破裂强度的矩震级

图3中DE段为塑性变形阶段。随着外荷载加大，接近试样极限荷载时，应力-应变曲线增长逐渐变缓，裂纹急剧增长，呈现明显塑性破坏。从图4(d)和4(e)可看出,DE段破裂能量沿中轴线向中部扩展的速度迅速加快，声发射破裂强度也随之迅速增大，模型内部微裂纹不断萌生、贯通，逐渐形成主裂纹。

图3中EF段为破坏阶段，此时试样已经达到极限荷载强度值，应力-应变曲线急剧下降。在荷载的持续加载下，宏观破坏主裂纹会进一步扩展延伸并逐渐变宽，裂纹数急剧增长。F点为最终破裂阶段，试样形成了一条主要沿试样中轴线的宏观破裂带，导致试样最终失稳。同时，图4(f)中在破裂带处可观察到明显的分叉现象，对于MCS材料裂纹扩展过程中的分叉现象说明在应力的作用下裂纹选择具有最小阻抗力的不规则路径扩展，体现了材料的不均匀性。

图5为MCS声发射事件发生比率与破裂强度的关系。

由图5可以看出，当破裂强度在-6.75左右时，声发射事件发生的概率最大，即具有此破裂强度的声发射次数最多。在破裂强度为-7.5和-6.0附近时，声发射事件的概率最低；当破裂强度在-5.79到-6.75之间时，声发射事件概率随着破裂强度的降低迅速升高，近似呈指数增加；当破裂强度在-6.75到-7.52之间时，声发射事件概率随着破裂强度的降低而迅速降低。声发射事件发生的概率与破裂强度大致服从正态分布。声发射的比率与破裂强度二者之间服从高斯曲线，拟合方程如式(6)所示：

y=-0.002+0.135e5.271(x+6.754)2

(6)

R2=0.966

式中：y为声发射事件发生比率；x为破裂强度。

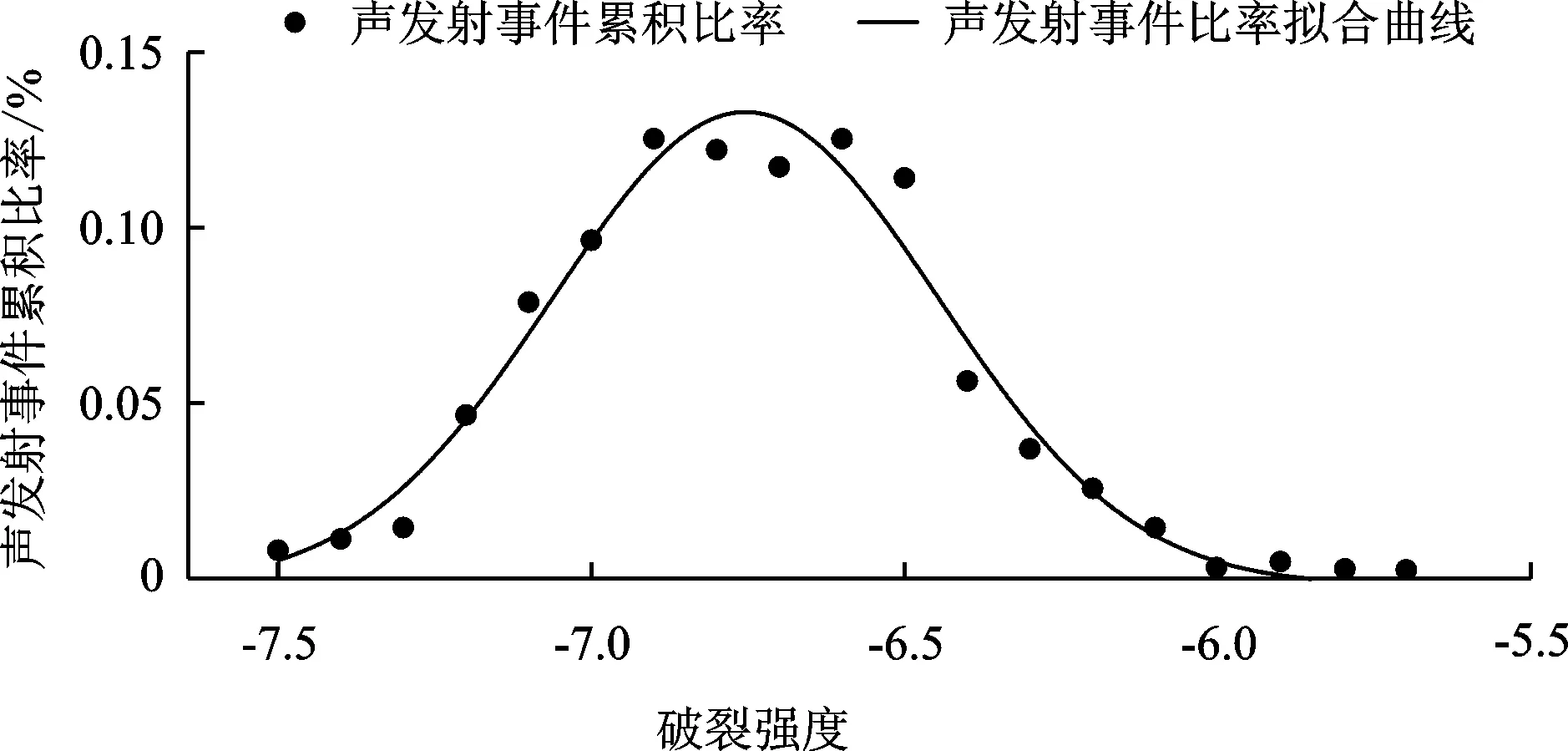
图5 声发射事件比率与破裂强度的关系

图6为声发射数目与微破裂数的关系图。

由图6可以看出，发生1条微破裂的声发射事件最多，共417次，约占所有事件的67.26%；仅包含2条微破裂的声发射事件次数为117次，约占声发射事件总数的18.87%。而包含5～10条(包含5条)和10条以上微破裂的声发射次数分别为26次和8次，占声发射事件总数的4.19%和1.29%。由此可得出结论，单次声发射事件产生的微破裂数与声发射数目呈负指数相关关系。在微破裂总数上，产生微破裂数最多为14条，产生次数为1次。

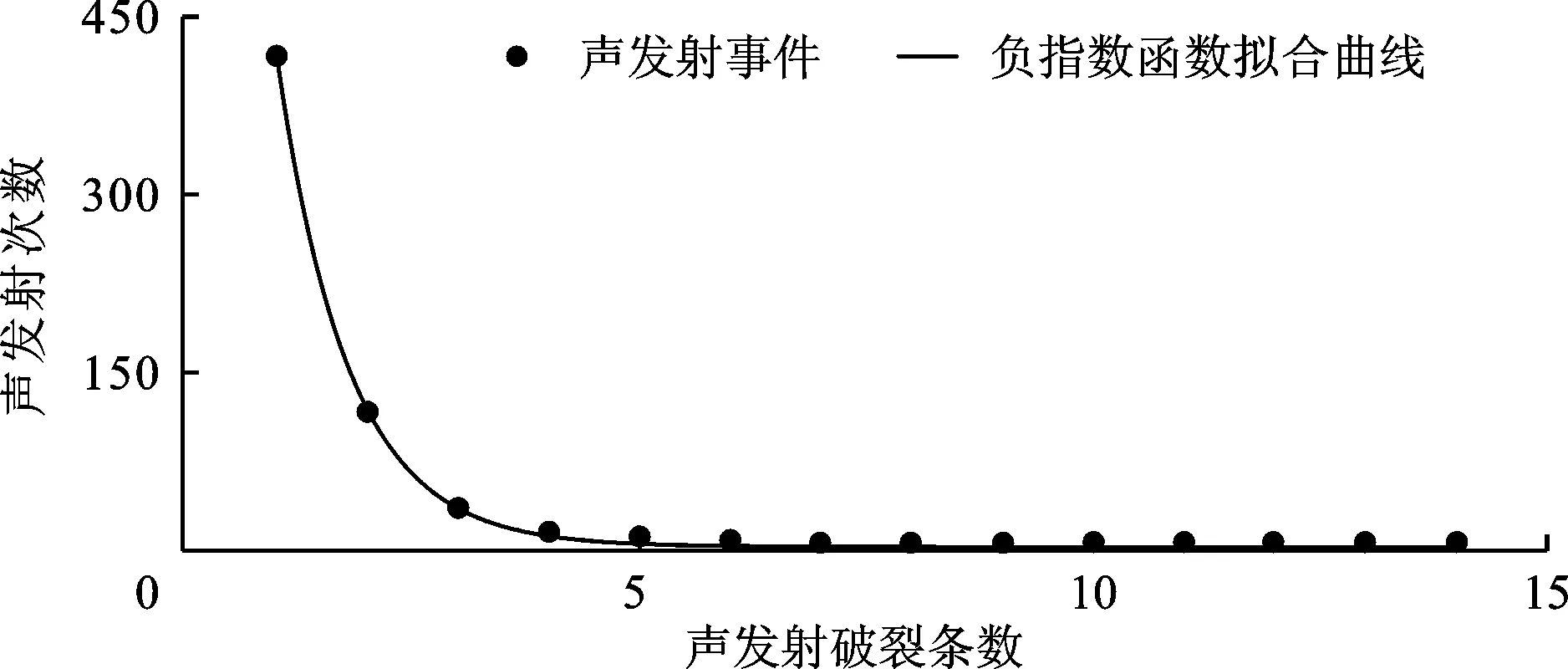
图6 声发射数目与微破裂数的关系

5 结 论

基于矩张量理论，从细观尺度研究MCS在巴西劈裂过程中的破裂过程，得到如下结论：

(1)MCS在破裂过程中，应变范围在0‰～3.0‰之间，试样最终形成主要沿中轴线的宏观破裂带，且由于MCS材料具有不均匀性，在破裂带处可观察到明显的分叉现象。

(2)声发射事件发生的概率与破裂强度大致服从正态分布。当破裂强度在-6.75左右时，声发射事件比率最高。

(3)单次声发射事件产生的微破裂数与声发射数目近似呈负指数函数关系。发生1条微破裂的声发射事件最多，占总数的67.26%。声发射事件产生最多的微破裂数为14条，仅发生1次。

基于矩张量理论的声发射模拟算法所开展的颗粒流数值模拟研究，为新型微生物建筑材料的细观研究提供了一种新的思路。然而本文研究成果仍然存在不足之处，由于MCS材料结构复杂，影响因素众多，本文对于MCS数学模型的构建精度有限，对于精度更高的模型的构建将是下一步研究的重点。