基于结构方程模糊评估模型的水利工程项目施工阶段风险研究

刘 波， 姜一天， 张郑贤， 金 婷， 姜新佩

(1.河北工程大学 水利水电学院， 河北 邯郸 056000; 2.河北工程大学 土木工程学院， 河北 邯郸 056000； 3.中国电建集团北京勘测设计研究院有限公司，北京，100038； 4.武汉大学 水利水电学院，湖北 武汉430072； 5.中国农业大学 经济管理学院，北京 100083)

1 研究背景

水利事业是保障国家快速发展的基础性行业，水利工程项目施工阶段在整个工程建设项目中位于最重要的地位，相比于立项阶段和后期管理阶段要复杂的多，风险事件频频发生[1]，因此，做好水利工程施工阶段风险评估具有重要的现实意义。

近年来，对工程项目进行风险评估也成为了工程建设必不可少的环节[2]。有不少学者对水利事业的不同方面进行了风险评估。风险评估的重点和难点在于风险因子权重的确定，其计算方法较多，常用的有层次分析法[3-6]、熵值法[7-8]、模糊综合评价法[9-10]以及模糊物元法[11-12]等。上述的研究方法中指标权重的确定均具有一定的主观性或者客观性[13]，忽略了指标间相互作用的复杂性。而结构方程模型是通过因子分析和验证性因子分析来确定各指标间的路径系数[14-15]，进而确定权重，能够克服上述方法确定权重的不足。

本文以水利工程项目施工阶段风险作为研究对象，综合运用结构方程模型和模糊综合评价方法，对现有项目风险评价模型进行了适应性改进，构建出结构方程模糊评估模型，进而对水利工程项目施工阶段风险进行评估。

2 结构方程模糊评估模型的建立

为了对水利工程项目施工阶段风险进行科学评估，本文在已有研究基础之上，综合运用结构方程模型与模糊综合评价法，构建了适合水利工程项目施工阶段风险评估的模型，即结构方程模糊评估模型。

结构方程模糊评估模型是运用结构方程模型确定各个风险指标的权重[16]，然后利用模糊隶属度函数构建出模糊综合评价模型[17]进行求解。其特点为：得到的评价结果明确，能够更好地适用于各类评价问题中，能够解决不确定因素的问题[18]。

2.1 建立风险评价指标体系

水利工程施工阶段风险评价首先需要建立评价指标体系，然后，需要对水利工程项目施工阶段收集相关指标数据。为了更充分体现风险评价信息，在制定评价指标体系时，需要考虑更多影响因素，进行筛选[19]，但是如果风险评价指标过多，容易造成风险评价体系的复杂性，复杂的评价体系又会带来更多的不可控因素，所以多方面考虑影响指标时，应舍去影响较小的指标[20]。

本文根据强跃等[6]对中小型水利工程施工指标的选取，再结合水利工程施工阶段具体情况，进行分析，可将风险评价指标分为5大类风险，其分别为质量风险B1、技术风险B2、管理风险B3、环境风险B4和其他风险B5。然后，结合水利工程实例，将各大类风险再细分为不同的小风险，即将n个风险指标设为Ci(i=1,2,…,n)。

2.2 确定模糊评价集

评语集是对每一因素所有可能评语的集合，根据水利工程项目施工阶段风险评估预期结果的形式来确定出评语集，如“高，中，低”。将水利工程施工阶段风险评价等级分为Ei(e1,e2,…,em)，有m个模糊评价集。

2.3 构建风险指标评判矩阵

确定模糊评价集之后，运用模糊评价集[21]对每个被评价事物从每个风险指标Xi(i=1,2,…n)上进行量化，即收集和整理各个风险指标的等级划分数据，来确定等级模糊子集的隶属度(R|Xi)，进而得到模糊关系矩阵:

(1)

式中：R为各个风险指标的隶属度集合；rij为某个风险评价指标Xi对风险指标的评价等级为Ej的模糊评价子集的隶属度。

2.4 确定评价因素的权重

确定各风险指标的权向量Wi(w1,w2,…,wn)。本文通过设计调查问卷的形式，利用结构方程模型确定风险评价指标间的路径作用系数，并对路径作用系数进行归一化处理，进而确定各个风险指标的权重。

结构方程模型[15](SEM)是第二代多变量数据分析方法，通常用来测量显变量与隐变量的关系。它可以用于测试理论支持的线性和非线性因果模型。SEM可用于处理研究性问题，处理不可观测的、难以测量的潜在变量。联立方程组为：

测量方程

x=Λxξ+δ

(2)

y=Λyη+ε

(3)

结构方程

η=Ψη+Γξ+ζ

(4)

式中：x、y为观测变量；Λx、Λy、Ψ和Γ为系数矩阵;η、ξ为潜在变量；ε、δ、ζ为误差项。

本文将目标层(A)和风险层(Bi,i=1,2,…,5)作为潜在变量，子风险层(Ci,i=1,2,…,19)作为观测变量。

一般运用Amos软件对结构方程模型进行计算，得到每个风险指标的协方差矩阵作用系数，即可得到各风险指标间的路径作用系数，即为协方差作用系数。然后根据公式(5)对协方差作用系数进行归一化处理，进而得到相应指标的权重系数[16]，其各个风险指标的权重组合记为W。

(5)

式中:WXi为风险因素X的第i个指标权重系数；λxi为风险因素B的第i个指标作用路径系数；X为风险因素(Bi,i=1,2,…,5)和子风险(Ci,i=1,2,…,5)；Xi为第i个指标的实际值；i为风险指标序号。

2.5 合成模糊综合评判结果向量

将水利工程项目风险指标的权向量W与各个风险指标的模糊隶属度关系矩阵R进行乘积，进而构建各风险指标的评判结果向量D即：

D=W×R

=(d1,d2,…,dn)

(6)

式中：di为被评价的水利工程风险评价指标对工程风险等级。

2.6 对评判结果分析

在工程风险评价算例中，最大隶属度原则是主要的参考依据，但由于水利工程项目在施工阶段的风险评估难以构成明显的数学函数关系，从而造成普通的最低隶属度原则难以合理评估出评价结果，因此本文提出运用加权平均的方法来求隶属度风险评价等级。

3 实例应用——M水库工程

M水库工程建于2016年，主要以防洪发电、节水灌溉等为主要任务，其最大坝高36.8 m，水库总库容为1.15×108m3，工程总投资18×108元，电站装机容量为7 MW。

3.1 建立风险评价指标体系

根据上述指标选取原则，结合该水库工程实例，将项目施工阶段的主要流程进行详细分析。本次具体从质量风险、技术风险、管理风险、环境风险和其他风险5大类中细分为表1所示的19个子风险指标，并对每个风险指标进行编号，将风险层编号为B，子风险层编号为C。

3.2 建立风险指标评价集

根据M水库工程实例，将风险评价等级分为3个等级[9]，分别为高、中和低。根据专家经验给出了各子风险3种等级的分数值的判断矩阵，各个风险指标风险等级评判矩阵见表1。

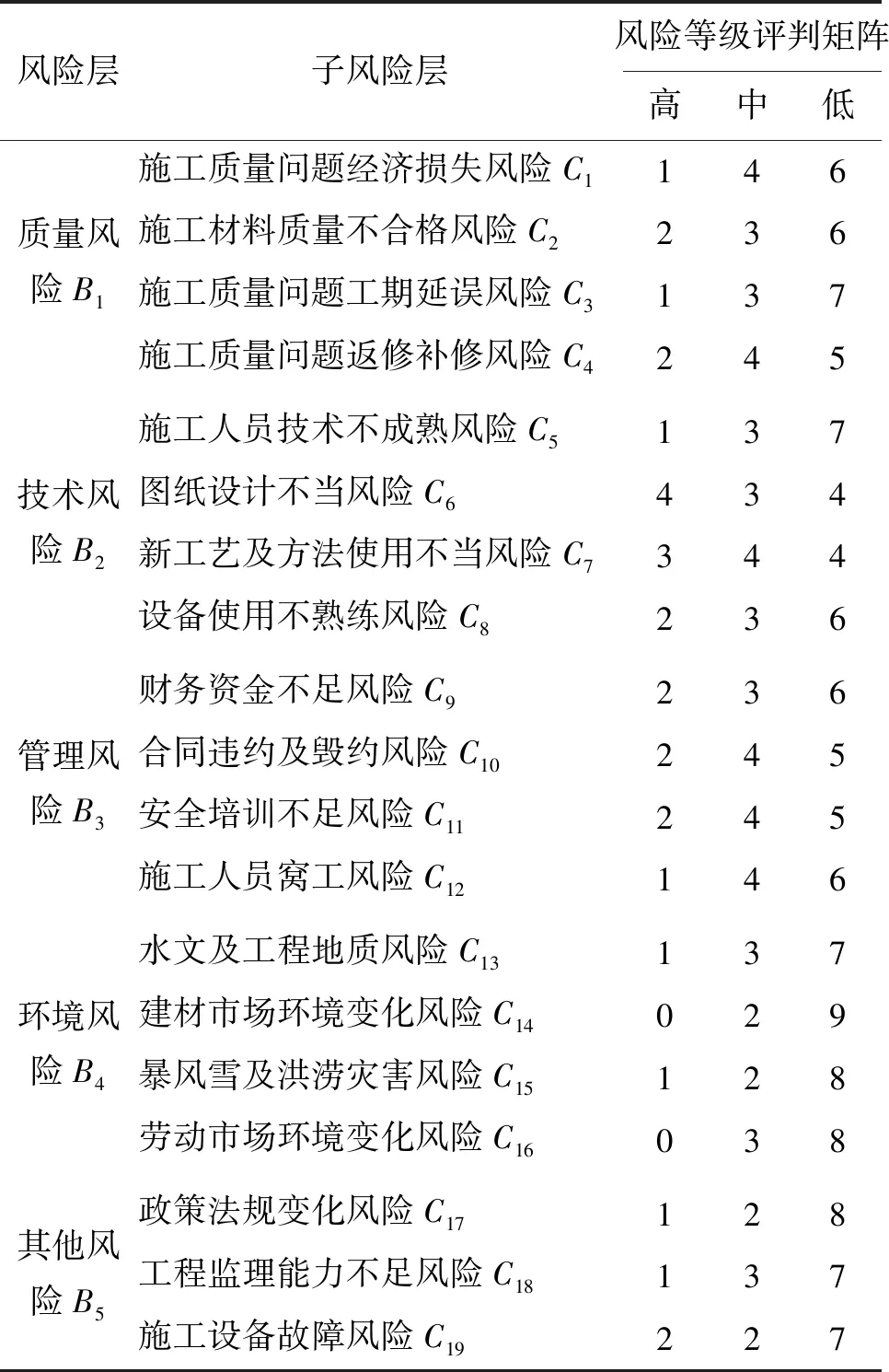
表1 各个风险指标风险等级评判矩阵

3.3 子风险层指标综合评价

(1)确定评价指标集。由表1可知，风险层评价指标有5个，即W={质量风险B1，技术风险B2，管理风险B3，环境风险B4，其他风险B5}；风险指标评价集有3个，即E={高，中，低}。

(2)确定各风险指标隶属度。以质量风险类为例，施工材料质量不合格风险隶属度为(R|X1)=(0.182, 0.273, 0.545)；施工质量问题返修补修风险隶属度为(R|X2)=(0.182, 0.364, 0.455)；施工质量问题工期延误风险隶属度为(R|X3)=(0.091, 0.273, 0.636)；施工质量问题经济损失风险隶属度为(R|X4)=(0.091, 0.364, 0.545)。在质量风险中各个风险因子的评价集为：

其他所有子风险层风险因子评价集为：

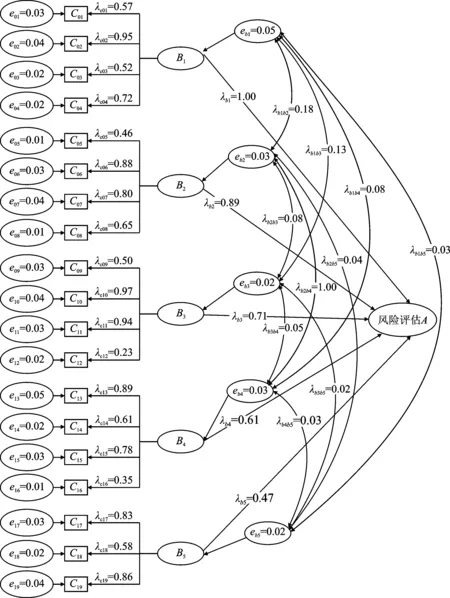
图1 各个风险指标路径系数

(3)确定各风险因子权重。在水利工程项目施工阶段风险评价研究中，按照表1中所罗列的指标对M水库工程的专家进行了问卷调查。为了保证数据的有效性，需要对调查的数据进行一系列的数据检验[22]。首先对数据进行信度检验，本次利用SPSS 22.0软件对M水库工程风险评估专家访谈表进行信度检验，α系数等于0.7352，表明风险指标数据可以接受，即信度检验效果较好。对数据进行KMO检验，检验值为0.8261；对数据进行Bartlett检验，得到的统计量sig值为0.00。因此本组数据可以用于研究分析。

利用Amos 22.0软件对结构方程进行了求解，求解时，首先将每一组的其中一个指标的路径系数设为1.0，进行运算求解得到其他所有指标的路径系数，选择标准化的路径系数如图1所示，图1中ei为误差项；λbi、λci分别为风险因素B、C的第i个指标作用路径系数；λbibj(i=1,2,…,5;j=1,2,…,5;i≠j)为协方差作用系数。

根据图1中各风险指标之间的路径作用系数，运用公式(5)进行标准化处理，得到风险层和子风险层的各个指标的权重，见表2。

表2 各个指标计算权重(结构方程模型)

以表2中质量风险为例，由4个权重因子组成的一个向量，WB1=(0.207,0.344,0.188,0.261)，采用加权平均算法计算质量风险等级的综合评价结果为：

D1=WB1RB1=[0.141,0.328,0.531]其中，0.141+0.328+0.531=1，说明该风险评价类型为归一的结果。

同理可得，技术风险、管理风险、环境风险和其他风险类的风险因子综合评价结果为：

D2=WB2RB2=[0.228，0.288，0.484]

D3=WB3RB3=[0.150，0.330，0.520]

D4=WB4RB4=[0.052，0.239，0.709]

D5=WB5RB5=[0.124，0.205，0.671]

3.4 风险层风险指标综合评价

风险层的风险指标为质量风险、技术风险、管理风险、环境风险和其他风险，其模糊权向量W=(0.272,0.242,0.193,0.165,0.128)，则风险指标综合评价结果为：

由以上结果可以得到，评定为高风险的比重为14.7%，评定为中等风险的比重为28.8%，评定为低风险的比重为56.5%。所以该水利工程施工阶段风险评价等级为低，该结果与实际评价结果一致。

3.5 层次分析模糊综合评价对比分析

利用层次分析法(AHP)[3-4]，建立与上述相同的评价指标体系，利用MATLAB 2014软件计算得到各个指标权重如表3所示。

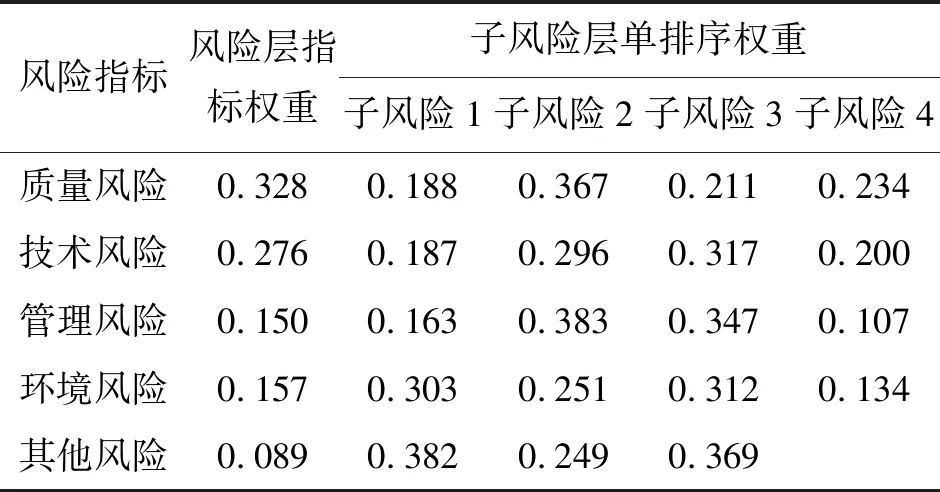
表3 各个指标计算权重(层次分析法)

运用AHP求解出了各个风险因子权重，下面结合模糊综合评价法对风险层的风险因子评估，其评估结果(计算方法同上，不再赘述)为：

D1=WB1RB1=[0.141，0.328，0.531]

D2=WB2RB2=[0.224，0.290，0.486]

D3=WB3RB3=[0.150，0.329，0.521]

D4=WB4RB4=[0.050，0.238，0.712]

D5=WB5RB5=[0.126，0.204，0.670]

最终，风险层的模糊权向量为：W=(0.328, 0.276, 0.150, 0.157, 0.089)，综合评价结果为：D*=[0.150, 0.292, 0.558]。

由上述计算结果得到该工程的施工阶段评定为低风险的比重为55.8%，所以该工程风险评价等级为低，与结构方程模糊评估模型结果一致。进一步验证了结构方程模糊评估模型可以应用在水利工程建设项目的风险评估领域。

通过结构方程模糊评估模型计算不仅得到了水利工程施工阶段各风险指标权重，而且得到了风险层风险指标Bi(i=1,2,…,5 )之间的协方差作用系数λbibj(i=1,2,3,4,5;j=1,2,3,4,5;i≠j)。由λb1b2=0.18、λb1b3=0.13可见技术风险对质量风险影响较大，管理风险对质量风险影响也相对较大；λb3b5=0.02表明管理风险对其他风险影响相对很小。所以在加强质量风险管理的同时也应加强技术风险和管理风险的管理。

在子风险层模糊综合评价时，发现新工艺及方法使用不当风险和施工质量问题经济损失风险的综合评价值最高，可见工艺方法和质量问题在施工阶段的重要性；在风险层模糊综合评价时，发现质量风险的综合评价值最大，说明质量风险造成的损失可能是最大的。因此，在水利工程项目施工阶段，应重点加强技术建设和质量建设，降低其风险影响程度。

4 结 论

本文运用结构方程模糊评估模型对水利工程施工阶段的风险进行了评估，并应用到M水库工程的施工阶段，得到以下结论：

(1)整个M水库工程的施工阶段风险评价等级为低，模型结果与实际工程和层次分析模糊综合评价结果一致，说明该模型可以较好地运用到水利工程项目施工阶段。

(2)根据模型计算得到风险层指标之间的协方差作用系数，能够发现指标间的相互影响程度，进而找到指标间的内在联系，为制定合适的规避方案提供依据。

(3)结构方程模型确定指标权重简单方便，比层次分析法节省大量计算步骤，从而可提高水利工程项目管理水平。对结构方程模糊评估模型在水利工程中的运用仅进行了初步探讨，在未来需要进行进一步研究。