基础设施建设与空间溢出关系的变化机制分析

王 斌，傅 强

基础设施建设与空间溢出关系的变化机制分析

王 斌，傅 强

（重庆大学经济与工商管理学院，重庆 400044）

本文以电网拓扑结构变化对区域能源强度的影响为例，揭示区域基础设施连接紧密程度对空间相关性的影响和其变化的内在机理。根据1998-2014年中国30个省份高压电网建设的时序顺序与拓扑结构构建空间权重矩阵，实现了基础设施动态建设与空间权重矩阵常数元素赋值的对应。使用SDM面板模型，并采用内生变量的滞后一期值代替原变量克服内生性偏误，得到了更为稳健的结果。研究发现：①考虑电网拓扑结构的空间溢出效应后，电力占比与要素结构提升对能源强度改善的影响得以体现，对外贸易的“污染天堂”效应被发现。②《大气污染防治计划》配套的12条高压电力线路改变了中国各省份能源强度的空间同质性，使得电力占比、产业结构、R&D研发水平对能源强度的影响变大；人均FDI存量、产权结构、要素结构、城市化率对能源强度的影响变小。③基于电网拓扑结构的空间权重矩阵能反映区域能源强度地理空间邻接关系的主要信息，通过强化和调整各省间的电网拓扑结构能够改变其空间溢出关系，促进政策目标的实现。此方法实现了省间基础设施连接紧密程度与经济指标空间相关性机理分析的计量方法应用创新。

电网拓扑结构；空间权重矩阵；空间杜宾模型；能源强度

0 引言

加强省间交通、能源、通信等领域的基础设施互联以促进经济发展是中国政府宏观管理的重要方向。2016年5月，国家8部委联合印发了《关于推进电能替代的指导意见》（发改能源[2016]1054号），提出了提高电力占比以提升能源利用效率的政策目标。国家电网公司作为主要执行者，大力推进特高压电网战略，试图通过加强省间的电网设施互联强化电力占比提升对能源效率提高的政策效果，受到了广泛的关注与讨论。那么，加强跨省高压输电通道的建设是否能改变能源强度的空间相关性，从而促进能源效率的改善？本文以此为例，进行空间权重矩阵的应用创新，应用空间计量方法量化分析省间基础设施互联对政策目标实现的价值。

关于能源强度的影响因素，国内外学者作了大量的研究。早期学者的研究，如史丹[1]、Fisher-Vanden et al[2]、魏楚[3]、傅晓霞[4]、原毅军[5]、林伯强[6]、张宇[7]、齐绍洲[8]等发现人均GDP、能源消费结构、FDI流入、产业结构、R&D研发水平、产权结构、要素结构、城市化率、对外开放程度、能源禀赋等经济指标均能影响能源强度。但是，上述研究未考虑各省能源强度的空间相关性，Elhorst[9]系统地总结了空间计量的研究成果，指出从计量分析的角度看，如果经济指标自身存在的空间相关性被忽略，则回归结果是有偏的；Toblers[10]从地理经济学的角度指出，区域间的地理位置越近，其经济联系应越紧密。随着空间计量经济学的发展，学者们将其引入了区域能源强度的研究，孙庆刚等[11]采用最近K点赋值法，按省份间的地理邻接关系划分为一阶、二阶与三阶相邻，以此为依据对空间权重矩阵赋值计算全局Moran’I指数，发现中国省间的能源强度空间依赖性随距离扩展逐渐减弱，一阶邻接关系下空间正相关依赖性最强，二阶邻接关系下空间关联性减弱，三阶邻接关系下已不存在统计上显著的空间依赖性。潘雄锋等[12]采用DEA方法分析能源效率，采用Rook邻近的空间权重矩阵方法使用SLM模型对其影响因素进行分析，发现我国省域能源效率具有明显的空间溢出效应，且呈现出增强的趋势。计及省域能源效率的空间相关性后，发现第二产业占比上升、能源价格提升对能源效率有反向的影响，而技术进步对能源效率有显著的促进作用，能源结构对能源效率的影响不显著。关伟等[13]采用非期望产出的SBM模型测试生态能源效率，采用Rook邻近的空间权重矩阵方法使用SLM与SEM模型对其影响因素进行分析，发现中国省域生态能源效率呈现出显著的全局空间相关性与局部空间聚焦特征，地理空间相邻省份的生态能源效率呈现显著的正向空间依赖特性，第二产业占比提升、能源投资增加与交通基础设施建设不利于能源生态效率的提升，而经济发展、外商投资与人口数量增加对生态能源效率的提升有正向的作用。可见，考虑能源效率/强度的空间相关性后，研究结论有了明显的变化，区域能源效率的空间相关性不能被忽略。但是上述研究还存在两个问题：一是模型选择仅限于SLM与SEM的比较，缺乏对适用性更为普遍的SDM的分析与检验，忽略了各自变量的空间溢出效应的影响，导致忽略变量偏误。二是简单地根据地理空间邻接关系赋值空间权重矩阵，地理位置相邻并不一定意味着两省份之间的能源效率溢出关系显著，尚需有效的基础设施载体，否则无法对空间相关性变化的机理与改进方式进行探讨，并提出通过调整空间相关性改善能源效率的政策措施。

Elhorst[9]阐明SLM模式是解释变量空间相关项系数为零的SDM模型，SEM是被解释变量空间相关项系数，与解释变量空间系数和其空间相关项系数乘积项相反数相等的SDM模型，因此，SLM与SEM模型均嵌套于SDM模型。在计量分析上，空间面板模型相对于传统面板模型加入了被解释变量的空间相关项，带来内生性问题。Elhorst[14]提出采用最大似然法估算空间自相关项的系数以克服最小二乘法估算带来的内生性偏误。但是Lee和Yu[15]指出对于大N小T型的面板数据，采用最大似然法估计空间自相关项的系数将产生一定的偏误，并提出了误差修正方法。此方法得到了Elhorst[16]的认可，将其称为混合ML/BCLSDV方法。此外，Arrelano and Bond[17]用于动态面板系数估算的GMM方法也可用于空间自相关项系数的估算，邵帅等[18]采用系统GMM方法对动态空间面板的系数进行估算，以克服解释变量的内生性问题。但此方法也存在一定的缺陷，Elhorst[16]比较了GMM、混合ML/BCLSDV与混合GMM/BCLSDV方法，指出GMM方法的估算结果在大N小T的面板模型中存在严重的偏误，对于大N小T的面板模型，在N小于500的条件下建议采用混合ML/BCLSDV方法。

由于换流站（直流与交流转化的设备）建设的成本较高，导致直流输电线路为“点对点”的电力输送方式，及电源端所在省份与负荷端所在省份各建设一座换流站进行电力交换。如葛洲坝—上海±500kV直流输电线路，直接从湖北葛洲坝水电站输送电力到上海，途经省份不落点。因此，直流输电线路使得中国各省份实现了跨区域的电网连接，空间邻接矩阵不再受限于省份间地理位置是否相邻的影响，地理位置间隔较远的省份可以通过直流输电线路建设，在业已形成的电网拓扑结构的基础上对空间权重矩阵赋值，以改变其空间相关性。因此，通过基础设施建设改变空间权重矩阵从而调整经济变量的空间溢出关系有重要的学术价值和现实意义。

本文的贡献在以下三个方面：一是根据高压交流/直流线路建设时序，提出了一种新的空间权重矩阵构建方法，实现了基础设施动态建设与空间权重矩阵常数元素赋值的对应；二是应用适用性更强的SDM面板模型，对各省份能源强度与其影响因素进行回归分析，与SLM和SEM的回归结果进行比较，更全面地反映各影响因素对能源效率的直接效应和间接效应；三是在通过比较基于基础设施的空间权重矩阵与基于地理邻接关系的空间权重矩阵的SDM回归结果，对前者进行稳健性检验的同时，识别出省域能源强度空间溢出关系的变化机理。

1 理论模型

1.1 空间自相关指数

全局空间自相关：采用全局Moran’s I指数表示：

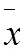
局部空间自相关：以能源强度为横坐标，能源强度的空间自相关项为纵坐标构建Moran散点图，按各省份所在象限分为HH（高—高，第一象限）、LH（低—高，第二象限）、LL（低—低，第三象限）与HL（高—低，第四象限）四种类型。其中分布于HH与LL的省份表示能源强度的分布为空间正相关，体现为空间同质性；分布于LH与HL的省份表示能源强度的分布为空间负相关，体现为空间异质性。

1.2 基于基础设施建设的空间权重矩阵设置

传统的空间权重矩阵根据研究对象的地理位置关系赋值，以反映其地理空间联系的程度，有三种类型：一是Rook邻近空间权重矩阵法，研究对象在地理位置上有共同的边界则在对应位置赋值1，否则赋值0，此种方法在目前的研究中使用最为广泛[11] [12] [13]；二是最近K点赋值法，即距离关系阈值预先给定，研究对象之间的距离小于给定值则赋值1，否则赋值0；三是距离关系赋值法，按照研究对象欧氏距离的倒数赋值，距离越短赋值越大。Lee and Yu[19]总结了空间计量研究成果，指出空间权重矩阵必须为常数阵，Elhorst[9]也坚持此观点。

由于空间权重矩阵W必须为常数阵。而基础设施的建设与投运具有时序性，使得各省间的基础设施网络拓扑结构呈现出随时间变化的特点，即新建基础设施的投运导致其拓扑结构的改变。如果按传统的方法对W进行赋值，基础设施投运年前后会得到不同的空间权重矩阵值。为解决此问题，采用基于基础设施投运时间的空间权重矩阵综合赋值法，如t年m月有新的基础设施投运，该设施连接省份i与省份j，则W中的i行j列元素表示为：

yrfinal表示研究时期的末年，yrstart表示研究时期的开始年份，yrt表示基础设施投产年份，m表示基础设施投产月份。模型(2)中的wij为0至1之间的值，越接近于1表示设施投产时期越早，对两省份之间的空间溢出效应贡献度越高，越接近于0表示设施投产时间越晚，对两省份之间的空间溢出效应贡献度越低。基础设施在yrstart年前投运，则相应位置赋值为1，在yrfinal年末还未投运，则相应位置赋值为0。完成赋值后再将空间权重矩阵W标准化，用于空间计量分析。同时，为实现分年度的全局Moran’s I指数计算与Moran散点图的绘制，定义各年度的空间权重矩阵W值为：

1.3 能源强度影响因素的理论模型

魏楚[3]通过能源效率的省级面板数据分析，发现“退二进三”的产业结构调整、微观企业层面的产权制度、要素禀赋结构、能源消费结构、R&D研发水平均对各地区能源强度有显著的影响，通过地区控制变量可见东部、中部的能源效率远高于西部地区。孙庆刚等[11]采用反映各省地理位置空间邻接程度的最近K点赋值法，发现城镇化率、对外开放程度、产业结构对能源强度变动有较强的解释力度，而能源价格的解释力度不显著。潘雄锋等[12]采用各省地理位置的空间邻接矩阵，发现中国省域能源效率的空间溢出效应显著且逐年增强，能源效率、技术进步对能源效率有显著影响。关伟等[13]发现中国生态能源效率呈现全局与局部空间聚集特征，产业结构对省域生态能源效率的影响最大。根据以上学者的研究成果，人均GDP、能源消费结构、FDI流入、产业结构、能源价格①现有研究[12]采用历年各省份的原材料、燃料、动力购进价格指数，2009年后更名为工业生产者购进价值指数）上年=100表示，但该指标不能单一地反映能源价格，而且由于采用上年=100的数据，造成该数据是一个比率，对数化处理后的经济意义不明确，故本文在能源效率的影响因素中不采用能源价格。、R&D研发水平、产权结构、要素结构、城市化率、对外开放程度、能源禀赋等经济指标均应作为能源强度的解释变量。

同时，中国省域能源强度/效率地理位置上的空间溢出关系已得到广泛的关注与研究，但是现有的研究仅仅是发现与验证了这种空间溢出关系，而没有对其产生与变化的机理作进一步探讨。由于各省间的基础设施连接是省间经济交流的基础，而地理位置相邻接省份的基础设施连接相对紧密，因此本文从各省的基础设施连接程度出发，采用Elhorst(2014)[9]中的SDM方法建模，以揭示各省份能源强度的空间溢出关系的变化机理。

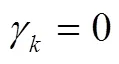
可见，SLM与SEM均嵌套于SDM中。

1.4 直接、间接效应

考虑空间相关性后，SDM中各解释变量的直接/间接效应为：

2 实证分析

2.1 数据来源及变量说明

本文样本为1998—2014年除西藏外的中国30个省市、自治区的面板数据。选取的各经济指标如下：

（1）空间权重矩阵（W）：以国家电网公司和中国南方电网公司2014年《电网运行方式报告》中的电网拓扑图为基础，找出省间500kV以上的电网连接线路。从历年《中国电力统计年鉴》中的重大工程部分找出相应线路的投运时间，按照公式(2)对空间权重矩阵进行赋值。

（2）能源强度（EI）：用各省份能源消耗总量与地区生产总值的比值表示，数据分别来源于《中国能源统计年鉴》和《中国统计年鉴》，地区生产总值数据折算为2014年价。

（3）人均GDP（PGDP）：用各省份的地区生产总值除以总人口数表示。各省人口数取自wind数据库。

（4）能源消费结构(ECS)：能源分为一次能源和二次能源，一次能源指直接取自自然界没有经过加工转换的各种能量和资源，包括：原煤、原油、天然气等；二次能源是由一次能源经过加工或转换得到的其他种类和形式的能源，包括煤气、焦炭、汽油、煤油、电力等。而电力被认为是清洁的二次能源，污染低能源利用率高。故采用电力在能源消费中的占比表示能源消费结构，各种能源消费数据取自《中国能源统计年鉴》，统一换算为标准煤。

（5）FDI流入（PFDIS）：用劳均FDI存量表示，即各省份FDI存量除以劳动力。用永续盘存法估算各省份FDI存量：FDISit=(1-d)FDISit-1+FDIit/Iit，其中FDIS表示资本存量，FDI表示外商直接投资额，用当年平均汇率转换为人民币计价。采用单豪杰[21]方法取折旧率d值为10.6%，Iit表示t年i省的固定资产投资价格指数。FDI数据来自各省统计年鉴，Iit数据取自《中国统计年鉴》，统一折算为2014年价。

（6）产业结构（IS）：采用第二产业增加值占GDP的比重表示，数据取自《中国统计年鉴》。

（7）R&D研发水平（RD）：用各省份历年R&D投入占GDP比重表示。2000年及以后的R&D数据来自《中国科技统计年鉴》，1998-1999年的R&D数据用科技投入数据替代。

（8）产权结构（OS）：采用各省历年国有及国有控股企业工业总产值占工业总产值比重表示。2012年以前数据取自《中国工业统计年鉴》，2013年后《中国工业统计年鉴》不再发布各省工业总产值数据，故采用各省历年国有及国有控股企业工业销售产值占工业销售产值的比重代替。

（9）要素结构(CL)：采用各省历年劳均资本存量数据表示。各省历年资本存量采用单豪杰[21]的方法估算，将重庆与四川资本存量分开估算，并将数据拓展到2014年，利用估算的价格平减指数将资本存量数据统一折算为2014年价。

（10）城市化率（UR）：2005-2014年数据来源于《中国统计年鉴》，2001-2004数据参考周一星[22]的方法修订得到,1998-2000数据则直接采用周一星[22]的修订值。

（11）对外贸易水平（TR）：采用各省历年进出口总额与GDP的比值表示，进出口总额来自国家统计局数据库。

（12）能源禀赋（ED）：采用各省历年劳均焦炭、原油、天然气产量数据折算为标准煤之和表示，数据来自《中国能源统计年鉴》。

2.2 能源强度的空间相关性分析

全局空间相关性：据方程(3)的方法分年度对空间权重矩阵赋值，以计算中国省际能源强度的全局Moran’s I指数，结果如图1所示。1998-2014年间中国省际能源强度的全局Moran’s I指数除1998年为零的显著性水平大于10%外，其余年份均为正值，显著性水平低于10%。全局Moran’s I指数总体上呈现出逐年递增的趋势，说明中国各省间的电力线路是一种有效的能源强度溢出渠道。由于各年份的全局Moran’s I指数均为正，说明省间高压电力线路的连接对能源强度的空间分布格局有很强的影响，有电力线路连接的省份，总体上能源强度趋于一致。

图1 1998-2014年基于电网拓扑结构权重矩阵的全局moran’s I指数

Figure 1 Global moran’s I from 1998 to 2014 based on the weighted matrix of power network topology structure

图2 1998、2006、2014年基于电网拓扑结构权重矩阵的moran散点图

Figure 2 Moran scatter plot based on weighted matrix of power grid topology structure in 1998, 2006 and 2014

局部空间相关性：根据方程(3)的方法分年度对空间权重矩阵赋值，得到1998年、2006年、2014年的Moran散点图，如图2所示。随着电网拓扑结构的加强，落于第一、三象限，呈现空间同质性的省份越来越多。1998年，由于新疆、青海、山东、海南和福建电网为孤网运行（电网与其他省份不相联），故其Moran散点图位于横坐标轴上（空间相关性为0）；到了2006年，只剩新疆、海南电网呈现孤网运行，故横坐标上只剩下两个点；到2014年初，所有省份的电网均与其他省份相联，不再有省份落于横坐标轴上，除个别省份表现为空间异质性的特征外，大部分省份均呈现空间同质性的特征。

可见，电网拓扑结构对各省份的局部空间相关性有显著的影响，随着时间的推移，电网拓扑结构加强，能源强度呈现空间同质性的省份越多，将一次能源丰富且能源强度较高的西部地区与一次能源相对匮乏且能源强度较低的东部负荷中心省份相连，可以通过空间同质性控制西部省份的能源强度。

2.3 稳定性检验

为避免伪回归，增强回归结果的可信性，须对各变量进行稳定性检验。面板单位根检验常用的方法有MADF(multivariate augmented Dickey-Fuller)、Im, Pesaran and Shin检验与Maddala, and Wu, Shaowen等检验方法，但是上述方法均只适用于小N大T型的面板数据。由于本文采用1998-2014年30个省份17年的面板数据，属于大N小T型的面板数据，故采用Levin, Lin and Chu (2002)[23]提出的面板单位根检验方法，判断解释变量的稳定性。

该检验的原假设为面板中的所有截面对应的序列都是非平稳的，备择假设为面板中所有截面的序列均是平稳的。各变量首先采用带时间趋势的滞后一阶形式，如不能拒绝原假设，再采用无时间趋势的形式进行检验，如依然不能拒绝原假设，认为该变量面板数据不稳定。检验结果如表1所示。

表1 稳定性检验

由表1可见，被解释变量ln(EI)与10个解释变量面板数据在10%的显著性水平上均拒绝原假设，即面板数据各数列均稳定，不存在伪回归问题。

2.4 能源强度的影响因素分析

现有的空间计量方法，主要关注空间自相关项的系数处理与修正[15][19] [16][9]，而对可能存在的解释变量内生性问题缺乏有效的处理方法。本节使用Davidson-mackinon(1993)的方法对解释变量的内生性进行检验，对存在内生性的解释变量使用其滞后一期值代替原变量进行空间回归分析，得到更为稳健的结果。

内生性检验：采用Davidson-mackinon(1993)提出的方法检验各解释变量(变量顺序如表2所示)是否存在内生性问题，原假设为所有解释变量与干扰项不相关（即解释变量是外生变量），使用其滞后1至8阶作为工具变量，得到Davidson-mackinon值分别为：32.77、0.99、0.15、0.28、3.67、0.66、4.99、0.24、7.16与0.09，对应的P值分别为0.00、0.32、0.70、0.59、0.06、0.42、0.03、0.63、0.01与0.76；表明人均GDP、R&D研发水平、要素禀赋与对外贸易水平对数值的外生性假设在10%的显著性水平上被拒绝，此四变量存在内生性问题，其余解释变量均可作为能源强度的外生变量。

按照方程(2)的方法，根据全国高压电网拓扑结构对空间权重矩阵W进行赋值，由于W的赋值已充分考虑了时间效应，故不再对时间效应进行分析。分别对碳排放强度采用SLM、SEM、SDM模型进行回归分析，结果如表2所示。

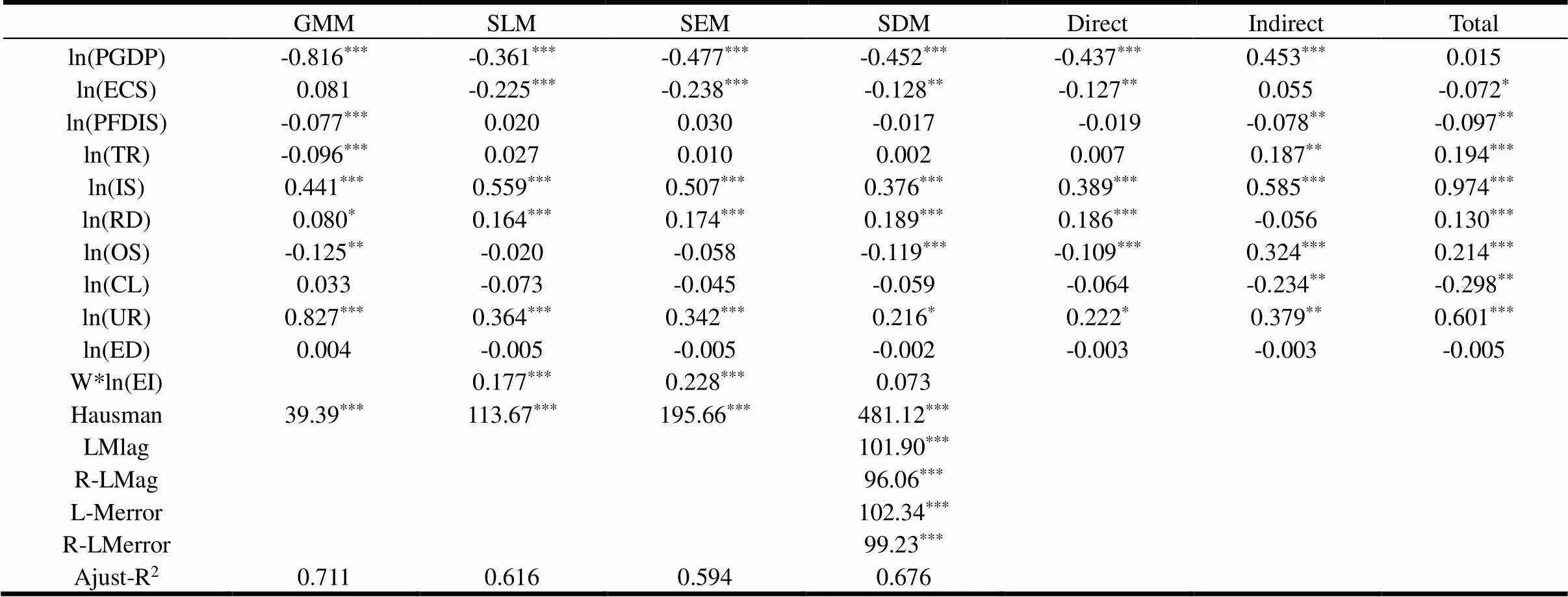
表2 能源强度的SDM回归分析

注：***、**和*分别表示1%、5%和10%的显著性，篇幅原因省去解释变量的空间相关项，下同。

直接/间接效益：为了检验直接/间接效应的统计显著性，采用Lesage and Pace(2009)[20]中的多变量残差正态分布法模拟最大似然函数，得到各影响因素的系数值，再使用t统计量判断其显著性。为保证结果的稳健性，模拟次数设为1万次，各影响因素的直接、间接与总效应如表2所示。

（1）人均GDP（PGDP）：GMM估算（不考虑空间溢出效应，下同）人均GDP的弹性系数为-0.816，在1%的水平下显著。考虑电网拓扑结构的空间溢出效应后，SDM中电力占比的弹性系数为-0.452，在1%的水平下显著。直接效应为-0.437，为0的显著性小于1%，表明各省份的人均GDP每上升1%，能源强度下降0.437%，表明各省份的经济发展模式已转变为能源节约型。间接效应为0.453，在1%的水平下显著，表明通过电网互联的邻接省份人均GDP上升1%，本省份能源强度上升0.453%。总效应的弹性系数不显著性，这是因为各省份人均GDP的直接效应显著为负，间接效应显著为正，二者之和为0.015，在10%的水平下不显著，即各省份人均GDP的变化对能源效率的影响不显著。SDM总效应的估算结果不显著，而GMM的估算结果显著，表明不考虑电网拓扑结构空间溢出效应，人均GDP对能源强度的影响会被高估；SLM、SEM中人均GDP的弹性系数显著，表明不考虑人均GDP的空间溢出效应，人均GDP对能源强度的影响也会被高估。

（2）能源消费结构（ECS）：GMM估算的电力占比弹性系数不显著，各省份电力占比的变化不能影响能源强度。考虑电网拓扑结构的空间溢出效应后，SDM中电力占比的弹性系数为-0.128，在5%水平下显著。直接效应为-0.127，在5%水平下显著，表明各省份的电力占能源消费的比重上升1%，能源强度下降0.127%。同时，电力占比的间接效应不显著，表明中国各省份的电力占比变化无法通过电网拓扑结构的空间溢出影响到其他省份。这是因为高压电网仅作为电力的传输渠道，还不是能源的主要传输形式；相对于煤炭消费而言，电力消费的量较小，电力传输渠道导致的能源强度空间溢出效应不显著。SDM总效应的估算结果显著，GMM的估算结果不显著，表明不考虑电网拓扑结构的空间溢出效应，电力占比对能源强度的影响会被忽略；SDM总效应估算结果的绝对值小于SLM、SEM，表明不考虑电力占比的空间溢出效应，电力占比对能源强度的影响会被高估。

（3）人均FDI存量（PFDIS）：GMM估算人均FDI存量的弹性系数为-0.077，在1%的水平下显著。考虑电网拓扑结构的空间溢出效应后，SDM中人均FDI存量的弹性系数为-0.017，不显著。直接效应为-0.019，不显著；间接效应为-0.078，总效应为-0.097，在5%水平下显著。总效应的绝对值大于间接效应，表明各省份的人均FDI存量上升1%，能源强度下降0.097%，FDI的“污染光环”效应较弱。SDM总效应估算结果的绝对值大于GMM，表明不考虑电网拓扑结构空间溢出效应，人均FDI存量对能源强度的影响会被低估；SLM、SEM中人均FDI存量的弹性系数不显著，表明不考虑人均FDI存量的空间溢出效应，人均FDI存量对能源强度的影响会被忽略。

（4）对外贸易水平（TR）：GMM估算对外贸易水平的弹性系数为-0.096，在1%的水平下显著。考虑电网拓扑结构的空间溢出效应后，SDM中对外贸易水平的弹性系数与直接效应均不显著。间接效应为0.187，总效应为0.194，在1%的水平下显著，表明考虑电网拓扑结构的空间溢出效应后，对外贸易水平占GDP比重上升1%，能源强度上升0.194%。SDM的总效应的估算结果符号与GMM相反，表明不考虑电网拓扑结构空间溢出效应，对外贸易水平对能源强度的影响会被错估；SLM、SEM中对外贸易水平的弹性系数不显著，表明不考虑对外贸易水平的空间溢出效应，对外贸易水平对能源强度的影响会被忽略。结合SDM中人均FDI存量的总效应可见，对外开放程度对能源强度的影响有正向和负向两个方面，外资会通过对外贸易的形式，将产业链中将高耗能、高污染的产能向中国转移；同时外资通过FDI流入的产能相对于国内较为先进，对能源强度的降低有略微的正向影响，但是，对外贸易占比上升对能源强度降低的负向影响大于正向影响。综合可见，对外开放程度越高，对能源强度上升的推动作用越强，“污染天堂”效应较为隐蔽。

（5）产业结构（IS）：GMM估算产业结构的弹性系数为0.441，在1%的水平下显著。考虑电网拓扑结构的空间溢出效应后，SDM中产业结构的弹性系数为0.376，在1%的水平下显著。直接效应为0.389，在1%的水平下显著，表明各省份的第二产业占比每上升1%，本省份的能源强度上升0.389%，因为第二产业的能源强度高于第三产业。间接效应为0.585，在1%的水平下显著，表明通过电网连接省份的第二产业占比上升1%，本省份的能源强度上升0.586%，因为各省份的第二产业聚集达到一定程度后，必然向其他省份溢出，而省份之间的电网连接保障了第二产业空间溢出的电力供应，促进了其空间溢出。SDM的总效应的估算结果大于GMM，表明不考虑电网拓扑结构空间溢出效应，产业结构对能源强度的影响会被低估；SDM总效应的估算结果大于SLM、SEM，表明不考虑产业结构的空间溢出效应，产业结构对能源强度的影响会被低估。

（6）R&D研发水平（RD）：GMM估算R&D研发水平的弹性系数为0.080，在10%水平下不显著。考虑电网拓扑结构的空间溢出效应后，SDM中R&D研发水平的弹性系数为0.189，在1%的水平下显著，因为R&D研发导致的技术进步是存在偏向的，分为生产技术和减排技术两类（邵帅等，2016），R&D研发投入偏好在很大程度上决定了技术进步对能源效率的影响。R&D研发的弹性系数为正，表明各省份的研发投入更多地用于生产技术的提高而非节能减排。直接效应为0.186，在1%的水平下显著；间接效应不显著；总效应为0.130，在1%的水平下显著，表明考虑电网拓扑结构空间溢出效应，R&D研发投入占GDP的比重上升1%，能源强度上升0.130%。SDM总效应的估算结果大于GMM，表明不考虑电网拓扑结构的空间溢出效应，R&D研发水平对能源强度的影响会被低估；SDM总效应的估算结果小于SLM、SEM，表明不考虑R&D研发水平的空间溢出效应，R&D研发水平对能源强度的影响会被高估。

（7）产权结构（OS）：GMM估算产权结构的弹性系数为-0.125，在5%的水平下显著。考虑电网拓扑结构的空间溢出效应后，SDM中产权结构的弹性系数为-0.119，在1%的水平下显著，直接效应为-0.109，在1%的水平下显著，表明本省份国有企业产值占比的提升有助于能源强度的降低。间接效应为0.324，在1%的水平下显著，表明通过电网互联省份的国有企业产值占比上升给本省份政府带来攀比效应，本省份政府为攀比电网连接省份国有企业产值占比上升带来的政绩压力，会放松对高耗能、高污染行业的管制，力争短期内提高工业产值以不落后于其它省份，导致能源强度上升。总效应为0.214，在1%的水平下显著，表明考虑电网拓扑结构空间溢出效应，各省份的国有企业产值占比上升1%，能源强度上升0.214%。SDM总效应的估算结果符号与GMM相反，表明不考虑电网拓扑结构空间溢出效应，产权结构对能源强度的影响会被错估；SLM、SEM中产权结构的弹性系数不显著，表明不考虑产权结构的空间溢出效应，产权结构对能源强度的影响会被忽略。

（8）要素结构(CL)：GMM估算要素结构的弹性系数不显著。考虑电网拓扑结构的空间溢出效应后，SDM中要素结构的弹性系数不显著，直接效应不显著。间接效应为-0.234，在5%的水平下显著，表明电网互联省份劳均资本存量上升1%，会导致本省份的能源强度下降-0.234%。这是因为电网互联省份的产业偏向于资本密集型，产业结构升级，则先进的技术会向本省份溢出，导致本省份能源强度降低。总效应为-0.298，在5%的水平下显著，表明考虑电网拓扑结构空间溢出效应，各省份劳均资本存量上升1%，本省份的能源强度下降-0.298%。SDM的总效应的估算结果显著，而GMM、SLM、SEM估算结果不显著，表明不考虑能源强度与要素结构的空间溢出效应，要素结构对能源强度的影响会被忽略。

（9）城市化率（UR）：GMM估算城市化率的弹性系数为0.827，在1%的水平下显著。考虑电网拓扑结构的空间溢出效应后，SDM中城市化率的弹性系数为0.216，直接效应为0.222，在1%的水平下显著，因为城市人口相对于农村人口，人均能源消费量较高。间接效应为0.379，为0的显著性水平低于10%，表明各省份之间的城市化率存在正向的空间溢出关系，而电网拓扑结构可以在一定程度上反映这种空间溢出关系。总效应为0.601，在1%的水平下显著，表明考虑电网拓扑结构的空间溢出效应后，城市化率上升1%，能源强度上升0.601%。SDM的总效应的估算结果低于GMM，表明不考虑电网拓扑结构空间溢出效应，城市化率对能源强度的影响会被高估；SDM总效应的估算结果大于SLM、SEM，表明不考虑城市化率的空间溢出效应，城市化率对能源强度的影响会被低估。

（10）能源禀赋（ED）：GMM、SLM、SEM与SDM的估算结果均不显著，这是因为中国各省份的能源调配与价格受中央政府的统一管控，一次能源产地的能源优势不显著。

2.5 加入12条电力线路后的电网拓扑结构对能源强度的影响

作为《大气污染防治行动》的配套政策，国家能源局于2014年5月发布《国家能源局关于加快推进大气污染防治行动计划12条重点输电通道建设的通知》。由于此12条线路在2014年后陆续开工，现有数据无法评估其对能源强度的影响效果，故采用林伯强等(2013)[6]所使用的反事实计量的方法，假设该12条线路在1998年初已建成投运，据此修改空间权重矩阵，再使用SDM进行回归分析。将回归结果与原空间权重矩阵的回归结果进行比对分析，识别出12条输电线路对能源强度的影响。在不考虑空间相关性的前提下，进行解释变量内生性检验，检测出人均GDP、R&D研发水平、要素禀赋与对外贸易水平为内生变量，其他解释变量为外生变量。SDM回归结果及直接/间接效应如表3所示。

加入12条高压电力线路后，电力占比的直接效应绝对值变大，间接效应变得显著，总效应绝对值变大，表明电网越密集，电力占比对能源强度的影响越大。人均GDP的直接效应绝对值变大，间接效应变小，总效应依然不显著，表明电网拓扑结构加强对人均GDP的弹性系数影响较小。人均FDI存量的直接效应、间接效应均不显著，说明电力线路的拓扑结构不能反映FDI的空间溢出效应。对外贸易水平的直接效应依然不显著，间接效应与总效应变小，电网拓扑结构的强化对对外贸易水平的影响较小。产业结构的直接效应与总效应变大，表明电网拓扑结构越强，第二产业占比提高对能源强度的影响越强。R&D研发水平的直接效应略微变小，总效应变大，表明电网拓扑结构越强，R&D研发水平提高对能源强度的影响越强。产权结构的直接效应不变，间接效应变小，总效应变小，表明电网拓扑结构加强后国有企业产值占比提升对能源强度的影响变小。要素结构的间接效应、总效应变得不显著，表明新增电力线路的方向不能反映要素结构的空间溢出效应。城市化率的直接效应变大，间接效应不显著，总效应变小，表明新增电力线路的方向与城市化率的空间溢出方向不一致。能源禀赋的直接效应、间接效应与总效应依然不显著。

可见，加入12条高压电力线路后，各解释变量的空间相关性发生变化，导致电力占比、产业结构、R&D研发水平对能源强度的影响变大；而人均FDI存量、产权结构、要素结构、城市化率对能源强度的影响变小；人均GDP、对外贸易水平对能源强度的影响不变。能源禀赋对能源强度的影响依然不显著。

表3 不同空间权重矩阵下的SDM模型回归结果

注：***、**和*分别表示1%、5%和10%的显著性；直接/间接效应求取时，正态模拟的种子值设为10000。

2.6 稳健性检验

电网拓扑结构能在多大程度上体现各省份之间能源强度的地理空间溢出关系？是否与目前研究中广泛采用的地理邻接空间权重矩阵[11][12][13所反映的空间溢出信息一致？为验证基于电网拓扑结构而设置的空间权重矩阵的稳健性，采用除西藏外的30个省份的地理空间邻接关系建立空间权重矩阵，再采用SDM面板模型进行回归分析。

从表3的地理空间邻接权重矩阵回归结果与表2的SDM回归结果对比可见：

（1）电力占比的直接效应绝对值变大，总效应变得不显著。表明电网拓扑结构空间权重矩阵能反映本省份电力占比变大，能源强度变小的信息，但反映幅度较小。

（2）人均GDP的直接效应绝对值变小，间接效应变得不显著，总效应不变。表明电网拓扑结构空间权重矩阵能反映本省份人均GDP上升，能源强度变小的信息。

（3）人均FDI存量的直接效应变得显著，间接效应与总效应变大。表明电网拓扑结构空间权重矩阵能反映人均FDI存量上升，能源强度变小的信息，但反映幅度较小。

（4）对外贸易水平的直接效应变得显著，总效应变大。表明电网拓扑结构空间权重矩阵能反映对外贸易总额占比上升，能源强度变大的信息，但反映幅度较小。

（5）产业结构的直接效应变得不显著，间接效应、总效应变小。表明电网拓扑结构空间权重矩阵能反映的对第二产业占比上升，能源强度变大的信息，但反映幅度较小。

（6）R&D研发水平的直接效应与总效应变大，间接效应变得显著。表明电网拓扑结构空间权重矩阵能反映R&D研发支出占比上升，能源强度变大的信息，但反映幅度较小。

（7）产权结构的直接效应符号相反，间接效应与总效应相同。表明电网拓扑结构空间权重矩阵能反映国有企业产值占比上升能源强度增大的信息，但对本省份直接效应的反映较差。

（8）要素结构的直接效应变得显著，但间接效应与总效应的符号相反。表明电网拓扑结构空间权重矩阵能反映的要素结构对能源强度的影响，与地理邻接空间权重矩阵不一致。按照产业资本密集程度越高，能源强度应降低的现象，电网拓扑结构空间权重矩阵的结果较为可信。

（9）城市化率的直接效应、间接效应和总效应变得不显著。表明电网拓扑结构空间权重矩阵反映的城市化率与能源强度的关系较为明确。

（10）能源禀赋的直接效应、间接效应与总效应的依然不显著。表明电网拓扑结构空间权重矩阵反映的能源禀赋与能源强度的关系，与地理邻接空间权重矩阵一致。

3 结论

本文以电网建设时序为例，提出了一种基于基础设施建设时序的空间权重矩阵构建方法，实现了基础设施动态建设与空间权重矩阵常数元素赋值的对应。采用内生变量的滞后一期代替原变量，克服了空间面板分析不注重解释变量内生性的问题，得到了更为稳健的结果。采用反事实计量的方法，根据拟建高压电力线路修改空间权重矩阵，识别出空间溢出关系的变化对能源强度的影响。将基于基础设施建设时序的空间权重矩阵SDM回归结果与传统的地理邻接空间权重矩阵SDM回归结果进行对比分析以检验其稳健性，主要研究结论如下：

一是考虑电网拓扑结构的空间溢出效应后，电力占比与要素结构提升对能源强度改善的影响得以体现。对外贸易的“污染天堂”效应被发现。二是《大气污染防治计划》配套的12条高压电力线路改变了中国各省份之间的空间同质性，使得电力占比、产业结构、R&D研发水平对能源强度的影响变大；人均FDI存量、产权结构、要素结构、城市化率对能源强度的影响变小。三是电网拓扑结构空间权重矩阵能反映地理邻接空间权重矩阵的主要空间溢出信息，通过强化和调整各省间的电网拓扑结构可以改变变量间的空间溢出关系，为通过强化基础设施建设而减少能源强度的政策措施提供了理论依据。本文的实用意义在于：本文提出的基于基础设施建设的空间权重矩阵方法实现了省间基础设施连接紧密程度与研究指标空间相关性变化机理分析的计量方法应用创新。

[1] 史丹.我国经济增长过程中能源利用效率的改进[J].经济研究, 2002(9):49-56+94

Shi D. The Improvement of Energy Consumption Efficiency in China’s Economic Growth[J].Economic Research Journal, 2002, (9):49-56+94

[2] Fisher Vanden K, Jefferson G H, Liu H, Tao Q. What is driving china’s decline in energy intensity?[J]. Resource and Energy Economics, 2004, 26(1):77-97.

[3] 魏楚,沈满洪. 结构调整能否改善能源效率:基于中国省级数据的研究[J]. 世界经济, 2008, 11:77-85.

Wei C, Shen M H. Can Structure Change Improve the Energy Efficiency? An Empirical Study Based on Provincial Data[J]. The Journal of World Economy, 2008, (11):77-85.

[4] 傅晓霞,吴利学. 中国能源效率及其决定机制的变化—基于变系数模型的影响因素分析[J]. 管理世界, 2010, 204(9):45-54.

Fu X X, Wu L X. The Efficiency of China's Energy Resources, and the Change in its Decisive Factors[J]. Management World, 2010, 204(9):45-54.

[5] 原毅军,郭丽丽,孙佳. 结构、技术、管理与能源利用效率[J]. 中国工业经济, 2012,7:18-30.

Yuan Y J， Guo L L， Sun J. Structure, Technology, Management and Energy Efficiency[J].China Industrial Economics 2012,7:18-30.

[6] 林伯强,杜克锐. 要素市场扭曲对能源效率的影响[J]. 经济研究, 2013,9:125-136.

Lin B Q, Du K R. The Energy Effect of Factor Market Distortion in China [J]. Economic Research Journal, 2013,9:125-136.

[7] 张宇,蒋殿春. FDI环境监管与能源消耗：基于能耗强度分解的经验检验[J]，世界经济, 2013,36(3):103-123.

Zhang Y. Jiang D C.FDI Environmental Regulation and Energy Consumption: An Empirical Test Based on Energy Consumption Intensity Decomposition[J], The Journal of World Economy, 2013,36(3):103-123.

[8] 齐绍洲,王班班. 开放条件下的技术进步、要素替代和中国能源强度分解[J]. 世界经济研究, 2013,(9):3-9+87.

Qi S Z, Wang B B. Technical Progress, Factor Substitution and China's Energy Decomposition under Open Economy Condition[J]. World Economy Study, 2013,(9):3-9+87.

[9] Elhorst J.P. Spatial Econometrics From Cross-Sectional Data to Spatial Panels[M]. SpringerBriefs in Regional Science, 2014.

[10] Tobler W R. Cellular Geography[J], Theory & Decision Library, 1979, 20(12):979-386.

[11] 孙庆刚,郭菊娥,师博. 中国省域间能源强度空间溢出效应分析[J]. 中国人口资源与环境, 2013,23(11):137-143.

Sun Q G, Guo J E, Shi B. The Analysis of Spatial Spillover Effect of Energy Intensity across Chinese Provinces [J]. China Population Resources and Environment, 2013,23(11):137-143.

[12] 潘雄锋,杨越,张维维. 我国区域能源效率的空间溢出效应研究[J]. 管理工程学报, 2014, 28(4):132-136.

Pan X F, Yang Y, Zhang W W. The Spatial Spillover Effect of China＇s Regional Energy Efficiency [J]. Journal of Industrial Engineering and Engineering, 2014, 28(4):132-136.

[13] 关伟,许淑婷. 中国能源生态效率的空间格局与空间效应[J]. 地理学报, 2015,70(6):980-992.

Guan W, Xu S T. Study on spatial pattern and spatial effect of energy eco-efficiency in China [J]. Acta Geographica Sinica, 2015,70(6):980- 992.

[14] Elhorst J P. Spatial panel data models, In:Fischer MM, Getis A(eds) Handbook of applied spatial analysis[M], Springer, Berlin, Herdelberg and New York, 2010a.

[15] Lee L F, Yu J. A spatial dynamic panel data model with both time and individual fixed effects[J], Econometric Theory, 2010a, 26(2): 564- 597.

[16] Elhorst J P. Dynamic panels with endogenous interaction effects when T is small[J]. Regional Science and Urban Economics, 2010b, 40(5):272-282.

[17] Arrelano, Bond. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations[J]. Review of Economic Studies, 1991,58(2):277-297.

[18] 邵帅,李欣,曹建华,杨莉莉. 中国雾霾污染治理的经济政策选择—基于空间溢出效应的视角[J]. 经济研究, 2016,51(9):73-88.

Shao S, Li X, Cao J H, Yang L L. China's Economic Policy Choices for Governing Smog Pollution Based on Spatial Spillover Effects [J].

Economic Research Journal, 2016,51(9):73-88.

[19] Lee L F, Yu J. Some recent development in spatial panel data models[J]. Regional Science & Urban Economics, 2010b, 40(5):255- 271.

[20] Lesage J P, Pace R K. Introduction to spatial econometrics[M]， CRC Press/Taylor & Francis Group, Boca Raton, 2009.

[21] 单豪杰. 中国资本存量K的再估算:1952～2006年[J]. 数量经济技术经济研究,2008,25(10):17-31.

Dan H J. Reestimating the Capital Stock of China: 1952～2006 [J]. The Journal of Quantitative & Technical Economics,2008,25(10):17-31.

[22] 周一星,田帅. 以“五普”数据为基础对我国分省城市化水平数据修补[J]. 统计研究, 2006,23(1):62-65.

Zhou Y X, Tian S. Amending the Data of Provincial Urbanization of China Based on the Data of the 5th Population Census [J]. Statistical Research, 2006,23(1):62-65.

[23] Levin, Andrew, Lin, et al. Unit Root Tests in Panel Data: Asymptotic and Finite Sample Properties[J]. Journal of Econometrics, 2002,108(1):1-24.

Analysis on the spatial spillover mechanism change induced by infrastructure construction

WANG Bin, FU Qiang

(School of Economics and Business Administration, Chongqing University, Chongqing 40044, China)

The interconnection of infrastructure such as transportation, energy, and communication among Chinese provinces is used to promote economic development effectively. But there is a lack of powerful quantitative methods to evaluate the effect of the intensity of infrastructure interconnection on various economic indicators. The paper explored the spatial correlation affected by infrastructure construction by considering the regional energy intensity affected by power topology structure. Electric power is considered to be of high quality, efficient energy. Improving the proportion of electricity in energy consumption can improve regional energy efficiency. The State Grid Corp uses the opportunity to implement the strategy of UHV power grid, by connecting the western region of China with rich energy resources with the eastern region with high load via the UHV power grid. Thus, the power substitution policy in the eastern region has a solid infrastructure assurance. However, it is unclear about how to evaluate the effect one the regional energy efficiency through power ratio promotion coming from inter-provincial high voltage power grid construction. It is also unclear about the mechanism of spatial correlation of energy intensity through inter-provincial high voltage transmission channel change to improve energy efficiency. These are the main problems that have to be solved urgently.

Firstly, A new spatial weight matrix confirmation method based on 1998-2014 Chinese high voltage power grid’s topology construction sequence and its topological structure is presented to reflect the infrastructure construction effect. Secondly, spatial Dubin panel model is adapted to overcome the ignored variables bias error, and the one-period lag value of the endogenous variable is used to control the endogeneity bias, the regression results are more robust. Thirdly, the counterfactual econometric method was adopted to analyze the effect on regional energy intensity caused by the 12 high voltage power lines that support the measures of "Air pollution prevention and control plan.” Finally, this study contrasts the results of the presented spatial weight matrix conformation method with those of the conventional spatial adjacency weight matrix to prove the rationality of the method.

Firstly, the interconnection of high voltage power grid among the provinces makes regional energy intensity trends to show spatial homogeneity. The more grid lines among provinces, the higher the spatial correlation. Secondly, promoting power proportion and factor structure can reduce regional energy intensity when considering spatial correlation affected by the power grid. The “pollution halo effect” of FDI existed but “pollution heaven effect” of foreign trade was discovered. The high consumption of energy and high pollution part of the industrial was quietly transferred to China through the integration of industrial chain by foreign capital. Thirdly, the operation of 12 high voltage power lines will change the spatial homogeneity among the provinces. The effects of power proportion, industrial structure, and R&D research and development level will be strengthened. The per capita FDI stock, ownership structure, factor structure, and urbanization rate will be weakened. Finally, the regression results using the spatial weight matrix based on the topology of the power network can reflect the major information of the spatial adjacency relationship of regional energy intensity. The spatial spillover effect of regional energy intensity can be changed by adjusting the power topology structure among the provinces. The results provide a theoretical basis for policy measures to reduce regional energy intensity. Infrastructure construction effect on the index reduction can be calculated by this method. This not only realizes the theoretical innovation of spatial correlation analysis mechanism but also provides a theoretical basis for the government to adopt energy-saving policies and measures.

Power grid topology; Spatial weight matrix; Spatial Dubin Panel model; Energy intensity

2017-03-03

2017-12-19

Supported by the Ministry of Education Layout Foundation of Humanities and Social Science (13YJA630018)

A

1004-6062(2020)01-0127-009

10.13587/j.cnki.jieem.2020.01.014

2017-03-03

2017-12-19

国家教育部人文社会科学研究规划基金项目（13YJA630018）

王斌（1983—），男，重庆人；重庆大学经济与工商管理学院，博士研究生；研究方向：技术经济与管理。

中文编辑：杜 健；英文编辑：Charlie C. Chen