服务机制设计与顾客分类服务定价研究

刘 健，张 帅，赵洪款，李兆斌

服务机制设计与顾客分类服务定价研究

刘 健1，张 帅1，赵洪款1，李兆斌2

（1.南京理工大学经济管理学院，江苏 南京 210094；2.南京航空航天大学经济管理学院，江苏 南京 211106）

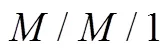
服务系统；排队论；顾客分类；定价策略；目标优化

0 引言

2015年，服务业实现的税收占全部税收的比重达54.8%，是我国税收主要创造者。服务业占比重持续上升，表明我国经济结构正在发生重大变化，转型升级已到了关键阶段，中国经济由工业主导向服务业主导加快转变，中国“服务化”进程已不可逆转，服务业已成为新常态下中国经济增长的新动力①2015年服务业引领国民经济稳步发展，中央政府门户网站，来源：统计局. http://www.gov.cn/xinwen/2016-03/10/content_5051710.htm。

排队是服务提供中一个非常重要的问题，其源于短时间内供给与需求的不匹配。由于顾客的异质性（即：顾客等待时间成本不同），为了提高排队的效率和顾客满意度，需要识别出顾客的异质性并在实施服务机制（策略）时根据其异质性进行有效的区分。服务提供商通过相应的排队机制来获取更多利润，这种针对顾客异质性的区分通常利用在服务系统中设置优先权（贵宾席）来实现。在服务系统中引入优先权选项设置之前，需要评估其预期效果，因此需要考虑以下问题：①优先权的设置在当前服务系统是否具有吸引力？②设置优先权是否能够增加企业收益？③应该对优先权加收多少服务费？④是否应该限制加入优先权的顾客数量或比例？

顾客等待时间成本是回答本文研究问题的关键，为了达到所述的研究目标，需要用一种合适的方法找到不同顾客等待时间成本之间的互异性，但总体而言，顾客时间成本的分析是非常复杂的，到目前为止几乎没有可能找到一个完美建模方分布和指数分布的等待时间成本函数。文献[4-5]通过将顾客的等待时间成本分割为不同的几种类型（同种类型顾客之间等待成本相同），针对上述问题进行相应研究，但作者并没有考虑相应的等待成本分布。

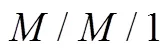
本文在研究过程中针对两种不同情形的服务系统进行分析：①垄断型服务系统（顾客不可选择退出或不能离开服务系统、产品替代性较弱、市场竞争不激烈或无竞争，顾客获得服务价值无穷大等）（如：签证受理服务等）；②非垄断型服务系统（顾客根据通过服务获得效用的大小来选择离开服务系统或留在服务系统、产品替代性较强、市场竞争激励或顾客获得的服务价值在一定范围之内等）（如：酒吧、餐厅或者游乐园等）。

本文创新之处：基于顾客时间成本均匀分布和收入函数分布，利用顾客效用函数，针对垄断型服务系统与非垄断型服务系统分析构造相应的服务定价函数、企业收益函数与服务系统总体顾客效用函数，从企业收益最大化视角，研究表明应对顾客进行分类服务来获得更大收益，并解决了对顾客进行服务分类的最优服务费用定价问题及相应顾客比例，在此基础上从服务系统总体顾客效用最大化视角出发，针对两种类型的服务系统研究表明应取消顾客分类服务。

本文主要框架：第二部分首先构建不同类型顾客的效用模型，然后对顾客效用模型选择进行分析，第三部分对企业收益进行优化分析，接下来在第四部分对顾客效用进行优化分析，第五部分对顾客等待时间成本为收入函数分布的情形进行数值模拟。基于上述两个优化视角分别针对两种服务系统的最优定价策略进行分析，并给出相应结论和管理启示。最后对本文的主要工作进行归纳总结，并指出未来的研究方向。

1 模型构建

1.1 效用模型

1.2 垄断型服务系统顾客效用选择

因此，顾客等待时间成本与顾客分类之间的关系如式(3)所示：

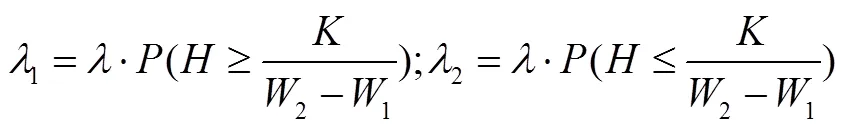
1.3 非垄断型服务系统顾客效用选择

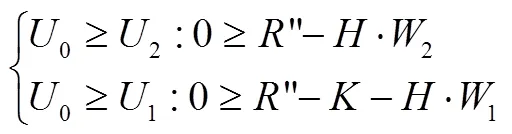
根据上面3个不同的约束关系，进行分析可知：

综上所述，可知针对顾客能够离开服务系统时存在下面两种不同的情况。

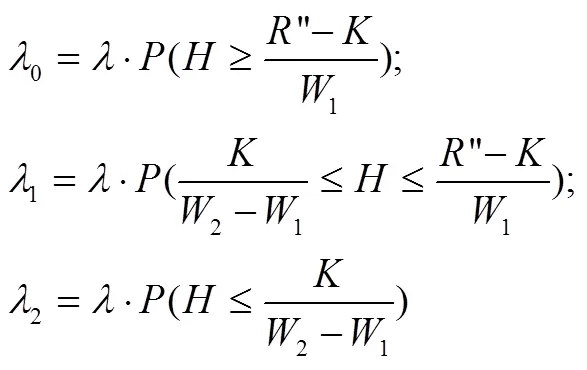
针对非垄断型服务系统，等待时间成本最高的顾客不论在哪种情况下都会选择离开服务系统。针对非垄断型系统存在的上述两种情况，接下来将会分别对其进行优化分析，然后综合比较，给出相应的服务定价策略与最优收益。

2 企业收益优化分析

2.1 垄断型服务系统

2.1.1企业收益函数

2.1.2 企业最优收益求解

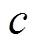
现实生活中，顾客进入服务系统后，根据获得服务价值，多数情形是可以自由选择离开服务系统，这时企业如何设置最优的优先权服务费用，是否应该对顾客进行分类服务，我们将在下一节对该情形进行详细阐述。

2.2 非垄断型服务系统

2.2.1 服务系统存在两种队列企业收益函数

根据顾客类型与时间成本的关系式(4)可得：

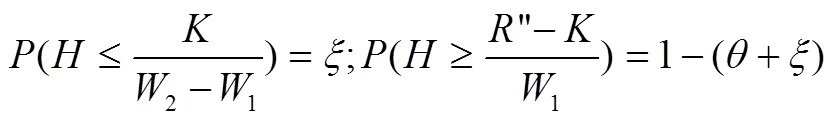
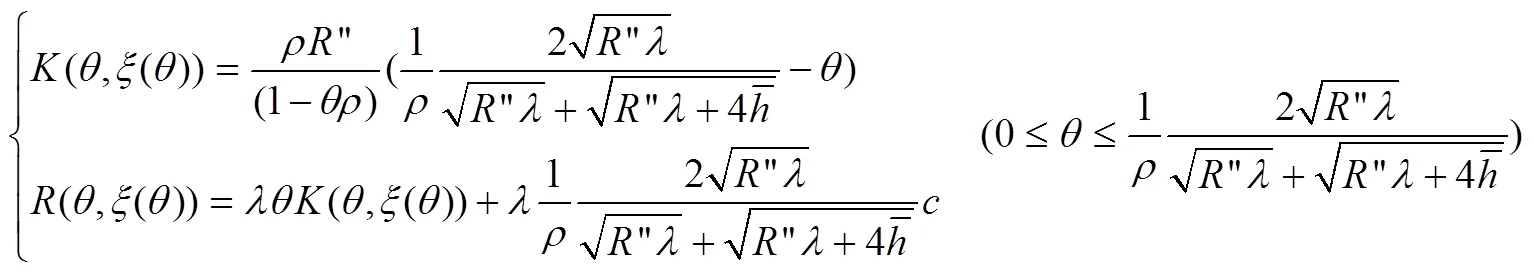
2.2.2 企业最优收益分析

根据上面的分析及表达式，针对非垄断型服务系统中有两种队列（顾客）存在时，可得服务提供商的最大收益值和对顾客进行分类服务的优先权定价及不同类型顾客相应的比例。

2.2.3 服务系统存在一种队列企业收益函数

显然，当顾客比例为固定数值时，企业的最大收益也为固定值，如式(12)所示：

2.2.4 两种情况分析

服务供应商采取两种队列（两种顾客）还是一种队列（仅有普通顾客），关键取决于哪种情形获得的收益更大。根据公式(10)与(12)中的企业最大收益值，可得下面的不等关系式：

管理启示2：针对非垄断型服务系统，服务供应商应仍然应对顾客进行分类服务（两种队列）来获得更大收益。

3 顾客效用优化分析

3.1 垄断型服务系统

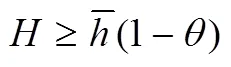
3.2 非垄断型服务系统

在定义域边界点处，顾客最大效用值满足如下等式关系

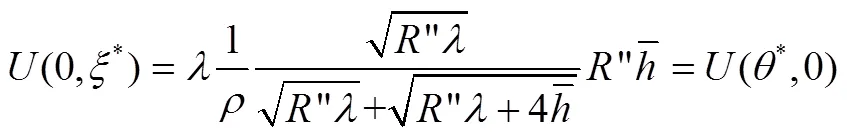
服务提供商取消顾客分类仅保留普通队列与服务提供商采取顾客分类但取消分类费用此时所有顾客都进入优先权队列，这两种情形下系统中顾客的效用是相同的。

管理启示3：从顾客效应最大化出发，在两种服务系统（垄断型服务系统或非垄断型服务系统）下，服务提供商都应取消顾客分类服务，仅保留普通顾客或者采取分类服务但不收取分类费用，此时所有顾客都进入优先权队列，与此同时，在这两种情形下，企业最大收益都是完全相同的。

4 基于等待时间成本为收入分布函数的服务机制分析

针对优先权顾客的最优比例，企业最大收益值和获取优先权服务的最优定价值，如表1所示。

表1 非垄断型顾客数值模拟最优结果数据表

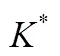
总之，从顾客效用最大化视角，我们得到与第4部分一致结论：服务提供商应取消顾客分类服务或采取分类服务但不收取分类服务费用。

5 结论

本文基于顾客等待时间成本均匀分布和收入分布，对垄断型服务系统与非垄断型服务系统的机制设计与顾客分类服务定价问题，从企业收益和顾客效用两个视角出发进行优化分析，并提出相应的管理启示。

本文主要做了四个方面的工作：①针对垄断型服务系统与非垄断服务系统分别构造了的服务定价函数与企业收益函数。②针对垄断型服务系统和非垄断型服务系统，解决了企业收益最大时，对顾客进行分类服务（获取优先权服务）的最优定价值及相应的优先权顾客与普通顾客比例。③从顾客效用最大化视角，针对上述两种服务系统，研究表明系统中仅保留一种队列（取消顾客分类服务仅保留普通顾客或取消顾客分类服务费用让所有顾客都进入优先权）时顾客效用最大。④当顾客等待时间成本为收入分布时，服务提供商仍然采取完全相同的策略。

根据本文研究，从企业收益（盈利性企业）角度出发应对顾客进行分类服务，从服务系统顾客总体效用（非盈利企业）最大出发应取消顾客分类服务仅保留一种队列。本文的主要工作可归纳为表2中内容。

表2 两种类型服务系统在两个不同视角下的最佳服务策略及分类服务定价值

本文研究过程中没有考虑排队过程中顾客的心理行为对顾客效用的影响，同时如何借助大数据技术准确刻画顾5BA2的时间成本分布函数，是我们未来需要深入研究的内容。

[1] Gavirneni S, Kulkarni V. Self-Selecting Priority Queues with Burr Distributed Waiting Costs[J].Production and Operations Management, 2016, 25(6): 979-992.

[2] Gavirneni S, Kulkarni V. Concierge Medicine Applying Rational Economics to Health Care Queuing[J]. Cornell Hospitality Quarterly, 2014,55(3):314-325.

[3] Yang L Y, Debo L, Gupta V. Trading Time in a Congested Environment[J]. Management Science, 2016, 63(7):2377-2395.

[4] Afèche P, Pavlin M. Optimal price/lead-time menus for queueing systems with customer choice: segmentation, pooling, and strategic delay[J]. Management Science, 2016, 62(8): 2412-2436.

[5] Afèche P, Araghi M, Baron O. Customer retention, acquisition, and service access quality: optimal advertising, capacity level and capacity allocation[J]. Manufacturing & Service Operations Management, 2016, forthcoming.

[6] Naor P. The Regulation of Queue Size by Levying Tolls[J]. Econometrica, 1969, 37(1): 15-24.

[7] Afeche P, Mendelson H. Pricing and Priority Auctions in queuing Systems with a Generalized Delay Cost Structure[J]. Management Science, 2004, 50(7): 869-882.

[8] Stanford D A. Waiting and Interdeparture Times in Priority Queues with Poisson and General-Arrival Streams[J]. Operations Research,1997,45(5):725-735.

[9] Kleinrock L. Optimum Bribing for Queue Position[J]. Operations Research, 1967,15(2): 304-318.

[10] Balachandran K R. Purchasing Priorities in Queues[J]. Management Science, 1972, 18(5): 319-326.

[11] Glazer A, Hassin R. Stable Priority Purchasing in Queues[J]. Operations Research Letters, 1986, 4(6): 285-288.

[12] 周文慧,黄伟祥,吴永忠,李合龙. 提高顾客等待满意度的两类排队管理策略[J].管理科学学报,2014,17(4):1-10+33.

Zhou W H, Huang W X, Wu Y Z, Li H L. Two kinds of queuing management policy for improving customer satisfaction with waiting[J]. Journal of Management Sciences in China, 2014,17(4): 1-10+33.

[13] Adiri I, Yechiali U. Optimal Priority-Purchasing and Pricing Decisions in Non-monopoly and Monopoly Queues[J]. Operations Research, 1974, 22(5): 1051-1066.

[14] 宋卫斌,苏秦.虚拟顾客服务系统排队模型[J].管理科学学报,2001,4(3):52-57+64.

Song W B, Su Q. Queuing model in virtual service support system[J]. Journal of Manegement Sciences In China, 2001,4(3):52-57+64.

[15] Mendelson H, Whang S. Optimal Incentive-Compatible Priority Pricing for the M/M/1 Queue[J]. Operations Research, 1990, 38(5): 870-883.

[16] Kim Y J., Mannino M V. Optimal incentive-compatible pricing for M/G/1 queues[J]. Operations Research Letters, 2003, 31(6): 459-461.

[17] Rao S, Peterson E R. Optimal Pricing of Priority Services[J]. Operations Research, 1998, 46(1): 46-56.

[18] Stidham S. Optimal Design of Queuing Systems[M]. New York: CRC press, 2009.

[19] Hassin R, Haviv M. To queue or not to queue: Equilibrium behavior in queueing systems [M]. New York: Springer Press, 2003.

[20] 程凤,霍佳震. 水平穿越法在带有不耐烦顾客的呼叫中心中的建模及应用[J].系统工程理论与实践,2013,33(5):1248-1254.

Chen F, Huo J Z. Modeling and application of level crossing in call centers with impatient customers[J]. Systems Engineering —Theory & Practice,2013,33(5):1248-1254.

[21] Nazerzadeh H, Randhawa R S. Asymptotic Optimality of Two Service Grades for Customer Differentiation in Queueing Systems[J]. University of Southern California Working Paper, 2014.

[22] Mendelson H, Whang S. Optimal Incentive-Compatible Priority Pricing for the M/M/1 Queue[J]. Operations Research, 1990, 38(5): 870-883.

[23] Gross D, Harris M C. Fundamentals of queueing theory (3rd Edition) [M]. New York: Wiley Press, 1998.

[24] Medhi J. Stochastic Models in Queueing Theory (2nd Edition) [M]. Boston: Academic Press,2002.

Service mechanism design and service pricing for customers segmentation

LIU Jian1, ZHANG Shuai1, ZHAO Hongkuan1, LI Zhaobin2

(1. School of Economics and Management, Nanjing University of Science and Technology, Nanjing 210094, China; 2. School of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)

Matching capacity with demand is a central theme in service operations management. Waiting occurs when capacity-demand mismatch happens, either due to insufficient long-term capacity or short-term fluctuations in-service load. Queuing is a significant issue in the service operation. There is a limited server capacity, and customers are heterogeneous in their waiting queue. The service provider usually segments customers into different classes and provides prioritized services based on this classification. Customers segmentation (classification service of customers) will reduce some customers’ waiting times and further improve satisfaction to extract the maximum revenue. How to design a scientific queuing mechanism for heterogeneous time-sensitive customers to extract the maximum revenue and customers’ utility for the service provider?

In this paper, we exact analysis of a non-preemptive M/M/1 queue problem based on the customers’ waiting cost (the time value of customers) follow a uniform distribution. We study both a monopoly service system (customers cannot leave the system) and a non-monopoly service system (customers are allowed free to leave the system and choose not to join any of the queues), respectively. From the perspective of revenue maximization and utility maximization, we study, analyze and explore when it’s optimal for the service provider to charge for priority service, and when it’s optimal for the service provider to provide only one type of service and not prioritize.

In the first part, by comparing the total utility of customers joining different queues, we will build the corresponding relationships between waiting costs and queues for customers. On this basis, the function of the priority fee for customer segmentation is constructed. Then, we will also obtain the function of the firm’s revenue and optimize it to get the optimal results. The results indicate that the service provider should take customers segmentation by charging a priority service fee and keeping two queues in both service systems to gain maximum revenue.

Then, we will get the optimal priority service fee for customers segmentation, the optimal proportion of priority customers and regular customers, and the optimal maximum revenue. Later, we build the corresponding function of the customers’ utility in two kinds of service system. Next, from the perspective of customer utility maximization, our study shows that in the above two kinds of service systems (monopoly service system and non-monopoly service system), the service provider should cancel the classification service of customers. Also, this study suggests that the company keep regular customers only in the queue or cancel the priority fee for customers classification and make all customers join the priority queue to obtain the maximum utility of customers.

Finally, we extend our research and study the customer's waiting costs follows a Burr distribution according to numerical simulation. We will get similar conclusions and insights in the above two kinds of service systems from the revenue and utility perspectives. The optimal priority pricing fee may be different under two waiting costs distribution, but it is completely consistent with the conclusion that the service provider should adopt customers segmentation (two queues) or not (one queue).

In summary, our results indicate that the service provider should approach this service design question differently depending on the different perspectives. Some original and interesting propositions are drawn based on our research, which will give important, scientific, and useful management insights into the corresponding service provider on service mechanism and pricing.

Service system; Queuing theory; Customer segmentation; Pricing strategy; Objective optimization

2016-12-31

2017-11-16

Supported by the National Natural Science Foundation of China (71671092, 71301075), the Natural Science Foundation of Jiangsu Province (BK20130770), theInternational Postdoctoral Exchange Fellowship Program (21040072) and the Jiangsu Postdoctoral Research Funding Program (1501040A)

F224

A

1004-6062(2020)01-0086-008

10.13587/j.cnki.jieem.2020.01.010

2016-12-31

2017-11-16

国家自然科学基金资助项目（71671092、71301075）；江苏省自然科学基金资助项目（BK20130770）；中国博士后国际交流计划派出项目（21040072）；江苏省博士后科研资助计划项目（1501040A）

刘健（1982—），男，山东淄博人；南京理工大学管理科学与工程系副教授，博士（后）；主要从事排队论研究。

中文编辑：杜 健；英文编辑：Charlie C. Chen