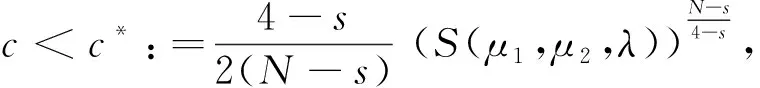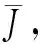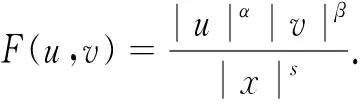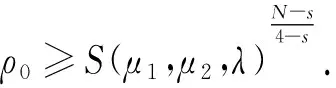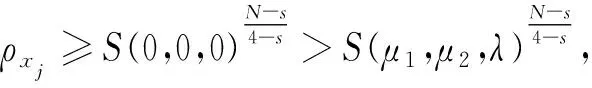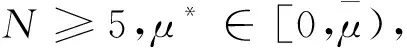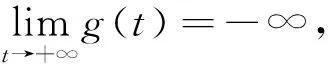带有耦合Rellich项的临界双调和方程组解的存在性

康东升, 田丹丹, 马玉恒, 曹玉平

(1 中南民族大学 数学与统计学学院,武汉 430074； 2 中南民族大学 图书馆,武汉 430074)

1 相关知识

在本文中，首先研究了下列双调和方程组：

(1)

其中参数满足下列假设：

这里D2,2(N)是N)关于范数的完备化空间，

(2)

其中Ω⊂N(N≥5)是包含原点的有界光滑区域，是外法向导数，a1,a2>0.

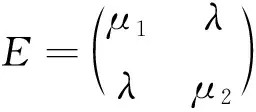
γ1(u2+v2)≤μ1u2+2λuv+μ2v2≤γ2(u2+v2),

其中γ1和γ2是矩阵E的特征值.

可以定义下列最佳常数：

S(μ*):=

由文献[2]可知，S(μ*)的达到函数是：

(3)

这里Uμ*(x)>0是一个径向对称的递减函数，满足：

根据Rellich，Sobolev和Young不等式[3-5]，可以定义下列最佳常数：

S(μ1,μ2,λ):=

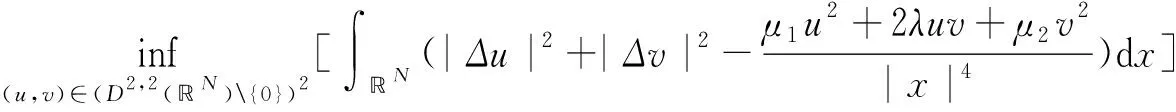
(4)

在积空间H×H上，方程组(2)对应的能量泛函是：

J(u,v):=

其中J∈C1(H×H,).在积空间H×H和它的对偶空间(H×H)-1中定义对偶积：

这里J′(u,v)表示能量泛函J在点(u,v)的Fréchet导数，(u,v),(φ,φ)∈H×H. 如果(u,v)∈H×H{(0,0)}满足：

J′(u,v),(φ,φ)=0,∀(φ,φ)∈H×H,

则称(u,v)为方程组(2)的解. 在方程组的所有解中，能量最小的解称为基态解.

定义下列函数和常数：

设Λ1(μ*)是算子L的第一特征值，定义如下：

考虑下面的条件：

(H2)N≥9,μ*≤ζ,0

本文的主要结果可以归纳为以下定理：

定理2假设(H1),(H2)成立，则方程组(2)存在一个非平凡解(u0,v0)∈(H{0})2.

为方便起见我们用C表示正常数，有时省略积分式中的dx. 对任意t>0和充分小的ε>0，o(1)表示一个无穷小量，O(εt)表示满足不等式|O(εt)|/εt

2 定理1的证明

定理1的证明假设(H1)成立，直接计算可得：

任取w∈D2,2(N){0}. 在(4)式中取检验函数对(u,v)=(w,Aw)，可以得出：

在上式中对w∈D2,2(N){0}取下确界即得：

S(μ1,μ2,λ)≤f(A)S(μ*).

(5)

设{(un,vn)}⊂D是S(μ1,μ2,λ)的极小化序列，令zn=snvn，其中：

于是就有：

(6)

由Young不等式可得：

由(6)式可以得到：

所以:

因为f(A)=f(B)，当n→∞时得出：

S(μ1,μ2,λ)≥f(B)S(μ*)=f(A)S(μ*),

(7)

由(5)和(7)式得出：

3 定理2的证明

证明假设序列{(un,vn)}⊂H×H满足：

J(un,vn)→c,J′(un,vn)→0在对偶空间(H×H)-1上，

易证序列{(un,vn)}在H×H中有界，则存在{(un,vn)}的子序列，我们仍记为{(un,vn)}，存在(u,v)∈H×H，使得：

(8)

(9)

F(un,vn)⇀dρ=F(u,v)+ρ0δ0,

(10)

(11)

(12)

因此有：

(13)

(14)

类似于(13)式，可得：

(15)

(16)

另一方面，由于：

(17)

O(ε2(b(μ*)-δ)),

进一步地，当N≥9时：

证明定义函数：

0≤μ*≤ζ⟺b(μ*)-δ≥2,

所以有：

g(tε)≤

定理2的证明由山路引理[8,9]，引理1和引理3可知，存在能量泛函J的一个非零临界点(u0,v0)∈H×H，它也是双调和方程组(2)的一个解；另外由假设(H2)中的条件a1≠0,a2≠0，可知(u0,v0)≠(0,0). 定理2证毕.