挡光片的宽度和振幅对阻尼振动半衰期测量的影响
2020-04-18任佳琪李飞祥彭雪城黄万霞
任佳琪,李飞祥,彭雪城,黄万霞
(安徽师范大学 物理与电子信息学院,安徽 芜湖 241002)
自由振动系统如果在振动过程中不断克服外界阻力做功,消耗能量,则振幅就会逐渐减小,经过一段时间后,振动就会完全停止. 这种振幅越来越小的振动叫做阻尼振动. 描述阻尼振动的模型称为弹簧振子模型,不仅可以描述机械运动,还可以描述RLC振荡电路中的电流和电压的变化[1],近几年来也被推广到微纳光子学中,用来描述微纳光子学中纳米颗粒的谱线[2],并进一步推广为双谐振子模型来描述模式间的耦合导致的各种现象:Fano共振、电磁诱导透明以及Rabi振荡等. 在光学开关、生物传感、信息储存、增强拉曼等方面有重要的应用. 基于以上的重要应用,弹簧振子运动特点研究成为普通物理实验中重要的实验. 近几年由于计算工具的发展,已有改进方案,例如利用智能手机和软件采集数据可以提高实验的准确性[3-8]. 但在传统教学中普遍采用光电计时装置,实验中测得的周期都很接近,不随振幅变化,而半衰期却受振幅影响. 利用弹簧振子体系从实验和理论两方面来探究挡光片宽度和振幅对半衰期测量的影响,发现半衰期的测量值与挡光片宽度在小范围内呈线性关系,且随着挡光片宽度的增加,实验测得的半衰期变大;而振幅则相反,随着振幅的增加,测得半衰期变小.
1 弹簧振子体系中推广的半衰期公式
劲度系数均为k的2根轻质弹簧,质量之和为m0,与质量为m′的滑块,按图1(a)所示的方式连接,其中O点为弹簧振子体系的平衡位置,P点为滑块静止释放的位置,Q为光电门的位置,且OP=A0,OQ=A0/2.w为挡光片的宽度. 为了讨论问题方便,把弹簧的质量等效加到滑块上,则弹簧振子体系的总质量为m. 在弹性恢复力和滑块与导轨之间的粘性阻力的作用下,弹簧振子的动力学方程为

(a)窄挡光片的起始释放状态
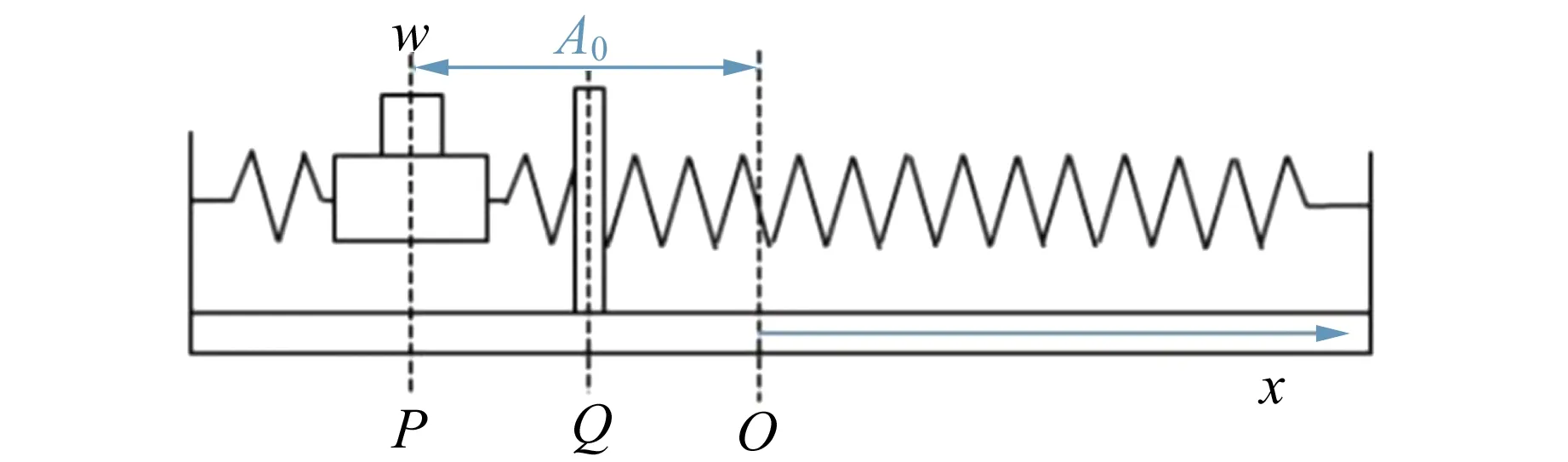
(b)宽挡光片时的起始释放状态

(c)宽挡光片的测量结束状态图1 气垫导轨简谐振动体系测量半衰期的原理图
(1)

(2)
在弱阻尼情况下,β2<ω02,式(2)的解为
x=A0e-β tcos (ωft+α) ,
(3)
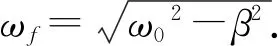
A=A0e-β t.
(4)
阻尼振幅减少到初值A0的一半所用的时间是半衰期Th,为了后面讨论问题的方便,定义Th为半衰期的真实值,由式(4)可得

(5)
由式(5)可解得半衰期为
(6)


(7)
从式(7)反解出半衰期的测量值Th′为
(8)
联立式(6)和式(8)得
(9)
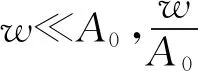
(10)
式(10)忽略高阶小量,只保留一阶小量,故式(10)进一步简化为
(11)
式(11)表明:在振幅一定的情况下,半衰期的测量值是挡光片宽度w线性函数,即随着挡光片的宽度的增大而增大,随着振幅的增大而减小. 基于式(11),可以得到计算半衰期的相对偏差η:
(12)
式(12)表明:相对误差与宽度w成正比,与振幅A0成反比. 因此在实验中,可以通过减小挡光片的宽度和增大振幅来减小实验误差.
2 实验装置和测量方法
实验所用仪器为气垫导轨、滑块、光电计时装置、挡光片和弹簧. 实验中所用的气垫导轨型号为QG-5-1.5 m,用MUJ-5C计数器来计算半衰期,实验配套的挡光片为黑色,其w=0.4 cm,为了研究挡光片宽度对半衰期的影响,用铝合金自制了棕色的4片挡光片,其宽度分别为0.4 cm, 1.0 cm, 1.5 cm和2.0 cm.
在实验中,首先将气垫导轨调节水平,将宽度为w的挡光片固定在滑块上. 找到平衡位置O点,将光电门放置在O点左侧A0/2的Q处,将滑块从O点左侧A0处P点无初速度释放,其中A0=20 cm,30 cm和40 cm. 滑块来回经过光电门2次计1个周期,当光电计时装置的周期数不再改变时停止计时,转化得到的时间即为半衰期.
3 挡光片的宽度对半衰期测量的影响
图2分别为不同振幅时实验测量和数值拟合的半衰期随着挡光片宽度的变化曲线. 从图2可以看出实验和理论符合得很好.Th′与w成线性关系,即半衰期的测量值随着挡光片宽度的增加而线性增大. 拟合得到的振幅为20 cm,30 cm,40 cm时半衰期的真实值Th(即图中的截距)分别为79.912 s,71.907 s,68.505 s. 当振幅不同时,拟合所得的半衰期的真实值不同,这表明半衰期与振幅也有关系. 由式(6)可知,半衰期与弹簧振子所受到空气阻力有关,阻力与速度有关,根据机械能守恒,振幅越大速度越大,对阻力与速度的线性关系有一定的影响[9],所以振幅的变化会影响阻尼因数β,因此振幅是半衰期的影响因素之一,故振幅不同时拟合所得的Th不同. 另外,实验中也制备了宽度小于0.4 cm的挡光片,发现该挡光片无法有效挡光,故光电门的发射光斑直径接近0.4 cm. 实验结果表明挡光片的宽度会影响半衰期测量结果,进而产生较大误差,要想尽可能地减小测量误差,理应使用宽度极小的挡光片,但是光电门计时器对挡光片的宽度是有要求的(宽度至少为0.4 cm),所以为了得到较为接近真实值的半衰期而将挡光片的宽度大幅度缩小是不可行的. 但我们所探究的实验为尽可能地得到接近真实值提供了一种符合实际方法,就是用不同宽度下的半衰期的测量值进行图像拟合,所得到的纵截距便是更加接近理论值的数值.
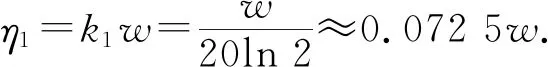
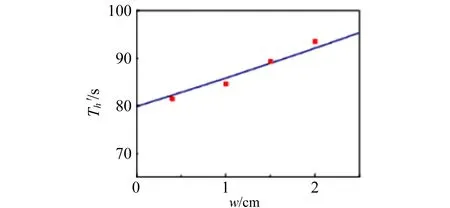
(a)20 cm

(b)30 cm

(c)40 cm图2 不同振幅时半衰期的测量值随挡光片宽度变化

(a)20 cm

(b)30 cm
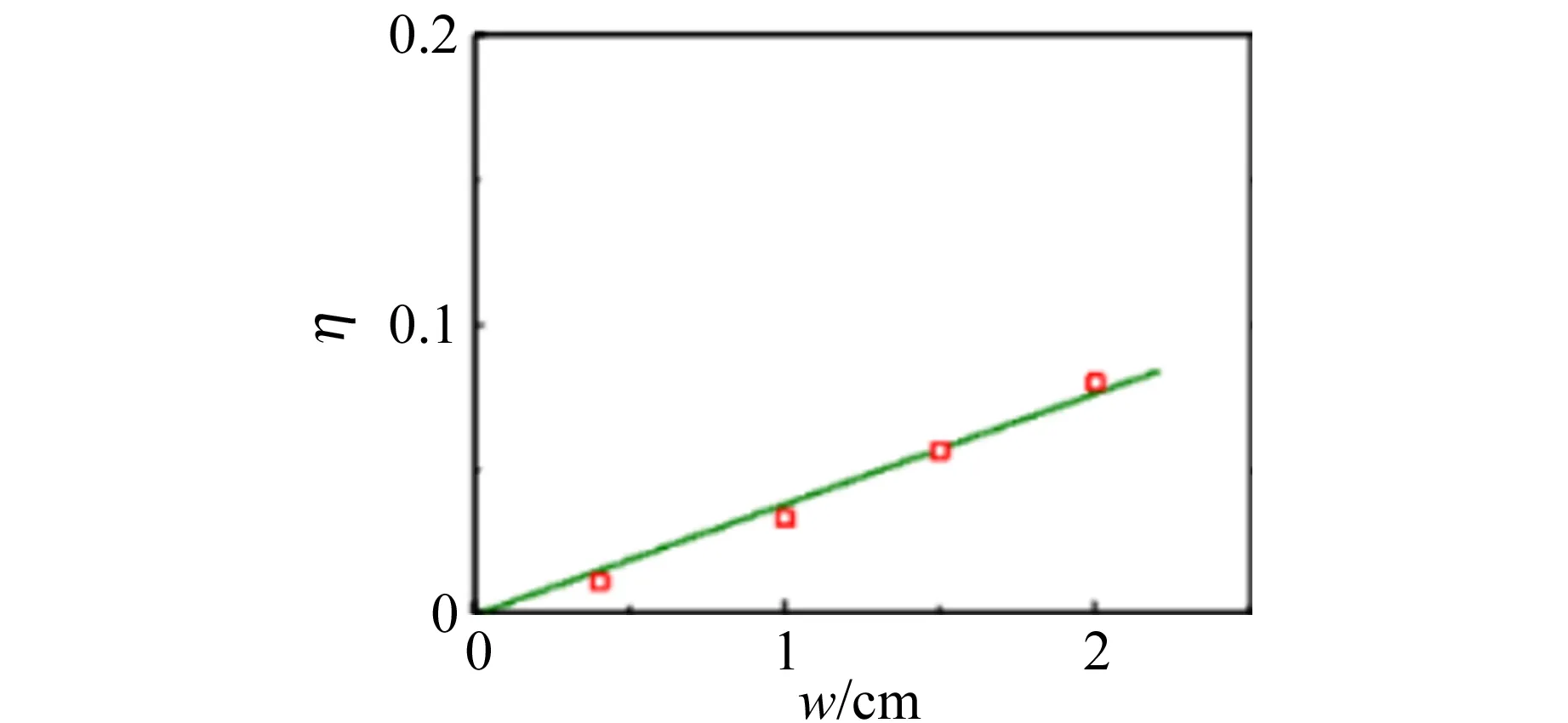
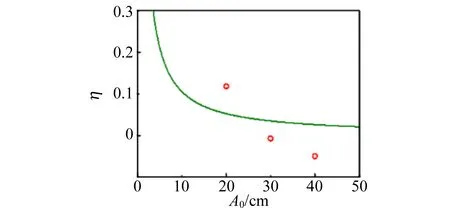
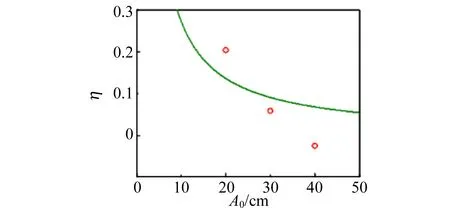
(c)40 cm图3 不同振幅时半衰期相对偏差随挡光片宽度变化
4 振幅对半衰期测量的影响
图4为挡光片宽度的不同时半衰期的测量随振幅的变化曲线. 从图4可以看出随着挡光片宽度的增大,半衰期增大;对于固定宽度后半衰期随着振幅的增大而减小. 为了研究实验的相对误差,基于式(12)绘出在给定挡光片的宽度时相对误差随着振幅变化的曲线,如图5所示. 从图5可以看出宽度越大,相对误差越大;对于某一固定宽度,相对误差与振幅成反比关系. 实验和模拟符合得较好,其差异主要来源于2个方面:不同的振幅对应的半衰期Th是有一定差异,而在拟合中采用的是同一个Th进行拟合的;振幅比较大时,空气阻力不再随速度成线性关系.
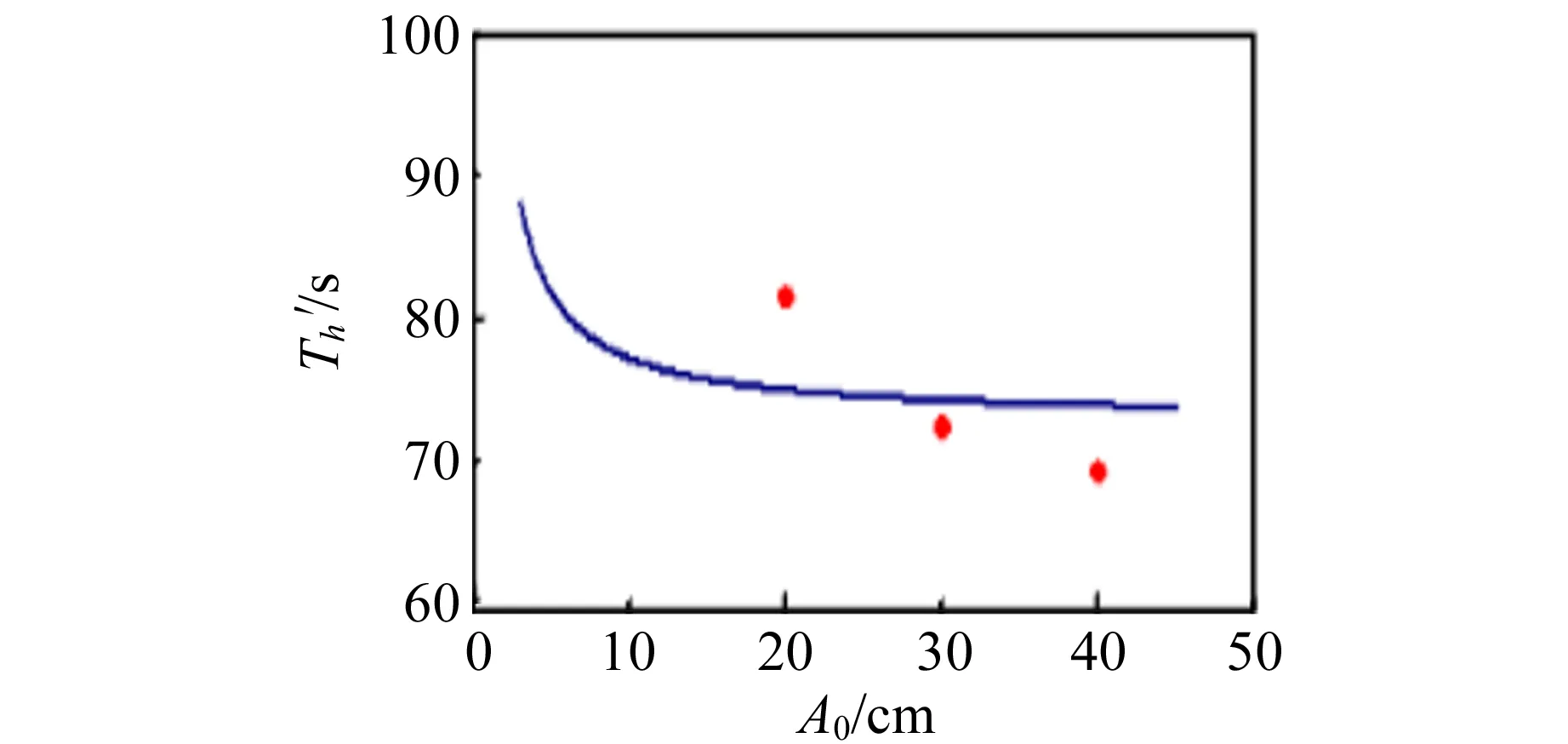
(a)0.4 cm

(b)1.0 cm

(c)1.5 cm
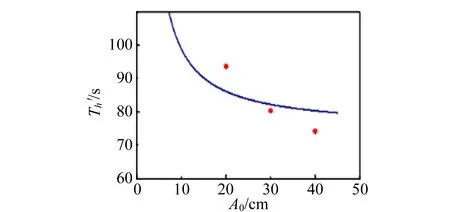
(d)2.0 cm图4 不同挡光片的半衰期的测量值随振幅变化
(a)0.4 cm

(b)1.0 cm
(c)1.5 cm

(d)2.0 cm图5 不同挡光片的半衰期的相对误差随振幅变化
5 结 论
利用弹簧振子模型研究了挡光片宽度和初始振幅对阻尼振动半衰期测量的影响,给出了宽挡光片的半衰期测量值的理论公式. 研究结果表明当体系初始振幅一定时,实验测得的半衰期随着挡光片宽度的增大而线性增大;当挡光片宽度保持不变时,测得的半衰期随着初始振幅的增大而减小,且相对偏差的绝对值先增大后减小. 理论和实验符合得很好.
