磁性斯格明子的研究:从金属到半导体
2020-04-18张慧敏
张慧敏,陈 军,董 帅
(东南大学 物理学院,江苏 南京 211189)
很多材料都具有磁性. 磁性的应用最早可以追溯到中国的司南,它被认为是指南针的起源. 如今磁性材料更是应用到了传统工业、生物医学、军事领域等各行各业,推动了现代社会的发展. 然而在信息时代飞速发展的时期,磁性材料最具价值的应用莫过于在数据存储领域中的应用. 例如巨磁电阻效应的发现,使硬盘尺寸极大地减小并使读取速度有了极大提高. 而发现巨磁电阻效应的法国科学家Albert Fert和德国科学家Peter Grünberg也同时获得了2007年的诺贝尔物理学奖[1-2].
随着人们对磁性的进一步认知,了解到磁性与电子的自旋密切相关. 鉴于磁性材料在未来的低能耗存储器件中的应用价值,从微观角度研究材料的磁性属性对探索新材料是非常重要的. 本文主要着手于斯格明子结构的微观产生机制,对斯格明子材料的发展进程和2个重要分类进行了简单介绍,并通过介绍尖晶石体系中的斯格明子相,给出了增强斯格明子稳定性的具体方法.
1 磁性斯格明子的研究进展
斯格明子是具有拓扑保护的一类稳定存在的结构,这个概念最早是在1962年由Tony Skyrme所提出来的[3]. 因为属于粒子物理的范畴,所以当时在这个概念提出后也并未得到人们的过多关注. 虽然之后也有相关的理论文章对其进行了报道[4],但是直到2009年斯格明子才首次在实验上被观测到. 德国慕尼黑理工大学的P. Böni课题组发表在《Sicence》杂志的文章报道[5]称,他们在手性对称的MnSi中探测到斯格明子[5].
在倒空间中形成的衍射点 (如图1所示[5]),提供了斯格明子存在的实验证据,而这一发现打开了研究斯格明子的大门[5],吸引了众多科学家们的关注. 之后,2010年日本科学家Y. Tokura等人在实空间观测到了斯格明子的拓扑螺旋结构 (如图2所示[6]),实现了真正意义上对斯格明子的观测[6]. 图2(c)和(d)中分别给出了实验观测到的以及蒙特卡洛理论模拟所得到的低温磁性相图,并且二者基本相吻合(图2中skx代表斯格明子相,H代表螺旋序). 至此,斯格明子成为了凝聚态物理领域非常引人注目的研究领域. 不过在如上的2个研究中,斯格明子相的存在必须要伴随着外加磁场的存在,而且存在的温度区间也非常窄. 不得不说斯格明子被观测到了,这的确是凝聚态物理领域非常重大的发现,但要真正的在器件中得以应用还需科学家们不断的探索.
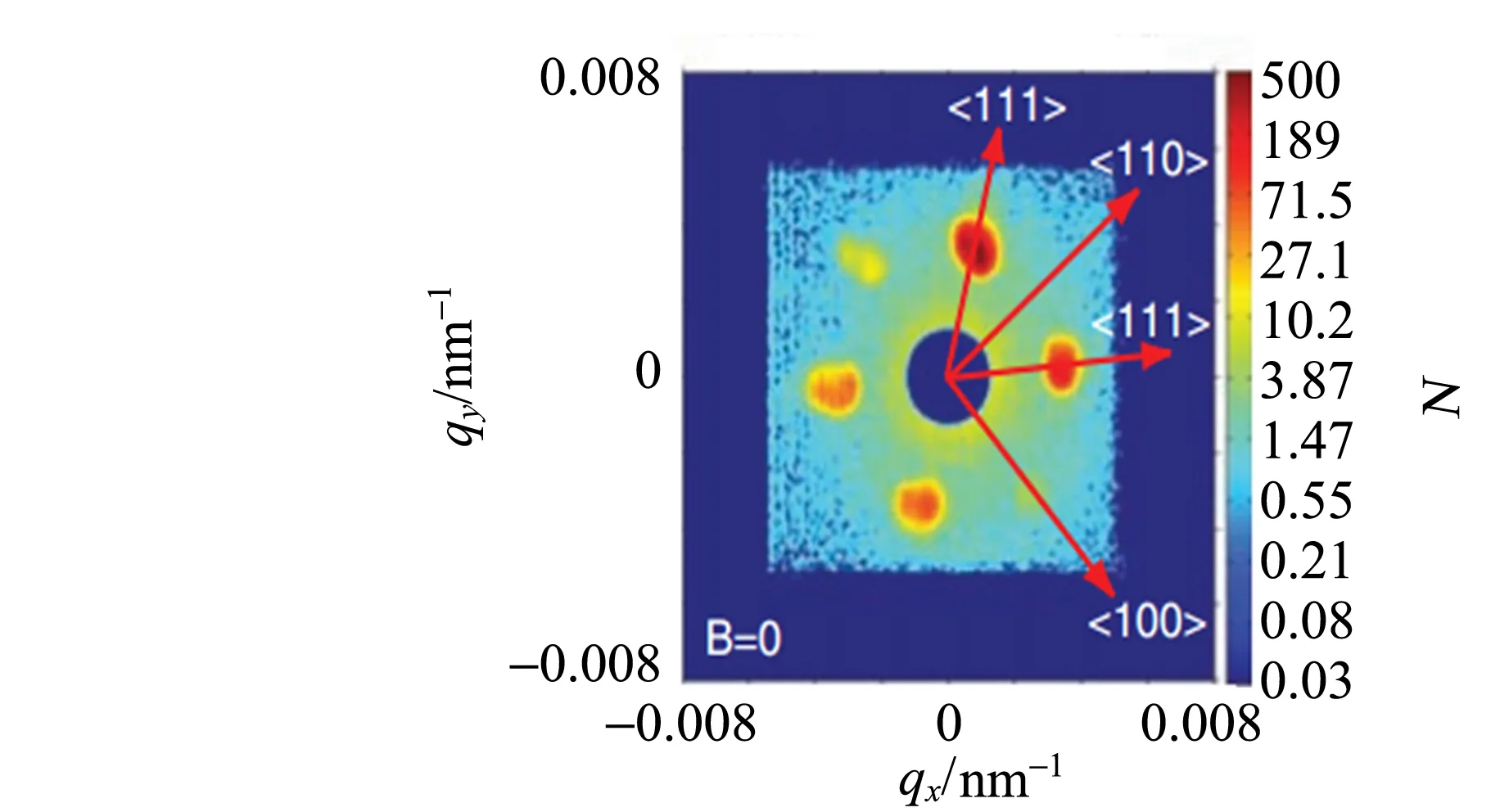
(a)螺旋序
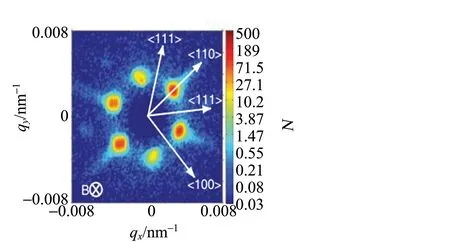
(b)斯格明子
图1 MnSi (样品1)中探测到斯格明子在倒空间中形成的衍射点

(a) 理论计算得到的螺旋序以及斯格明子相

(b) 实验上所观测到的螺旋序与斯格明子相
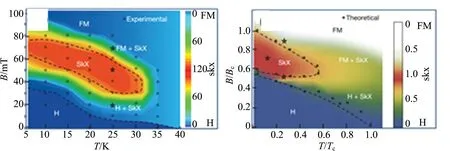
(c)外加磁场条件下,实验上所观测到的低温磁性相图 (d)外加磁场条件下,运用蒙特卡洛方法理论模拟所得出的低温磁性相图
1.1 斯格明子的分类
自从2009年斯格明子在实验室被观测到以后,最近10年对斯格明子的研究一直都受到了众多的关注,也逐渐发现了越来越多的斯格明子材料. 其中一些是块体材料,另外一些则是通过巧妙构建多层膜结构来产生斯格明子的. 从以往的研究结果看,斯格明子的产生多数是由于Dzyaloshinskii-Moriya相互作用(DMI)和磁交换作用相竞争,使自旋出现螺旋结构所导致的. 鉴于目前已经被报道过的存在斯格明子的材料,总结出对斯格明子的研究主要是关于Bloch型和Néel型的2类结构(如图3所示[7-8]).
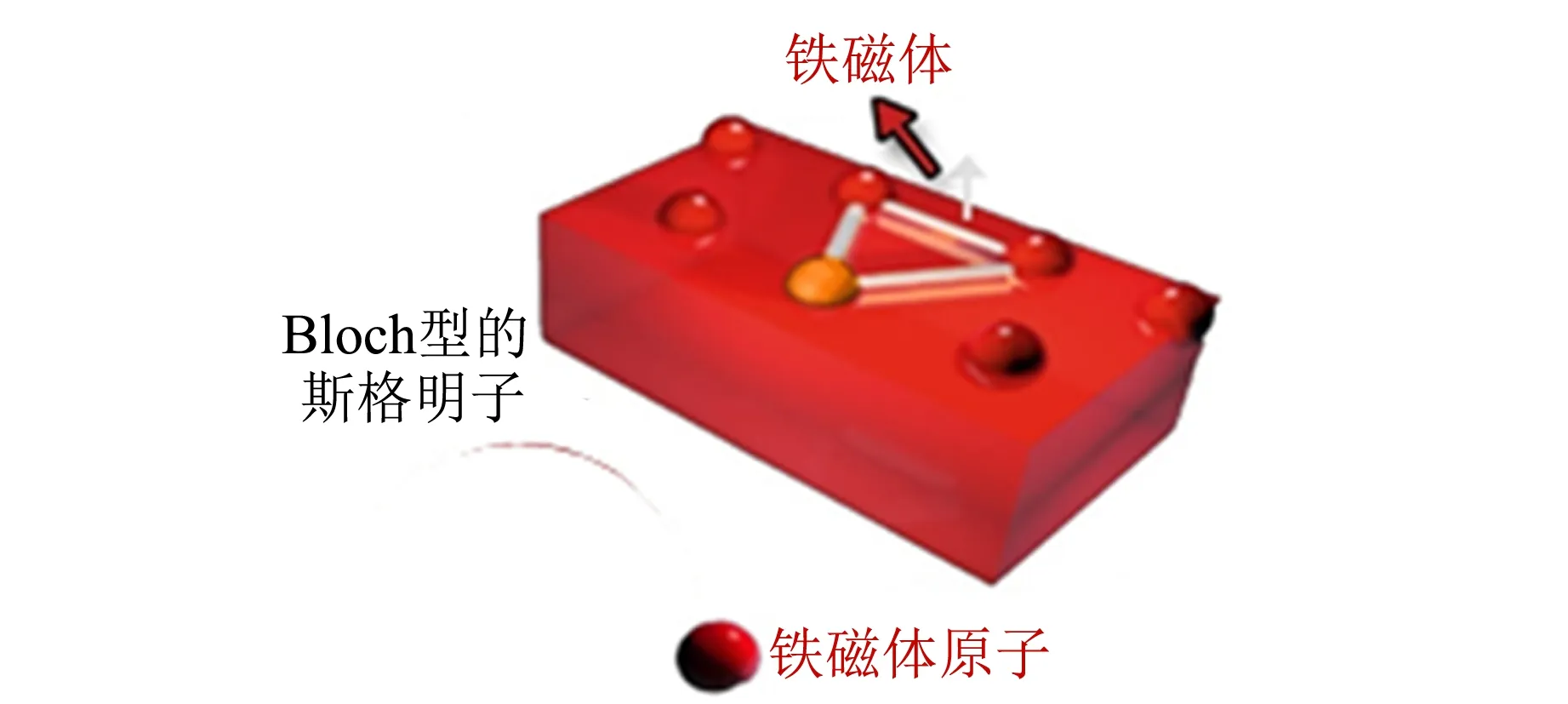
(a) Bloch型的斯格明子的形成机制
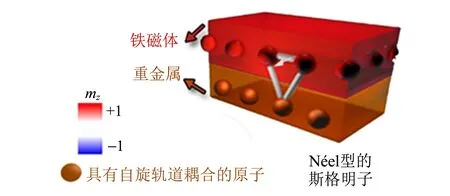
(b)Néel型的斯格明子的形成机制

(c) Bloch型的斯格明子的自旋结构示意图
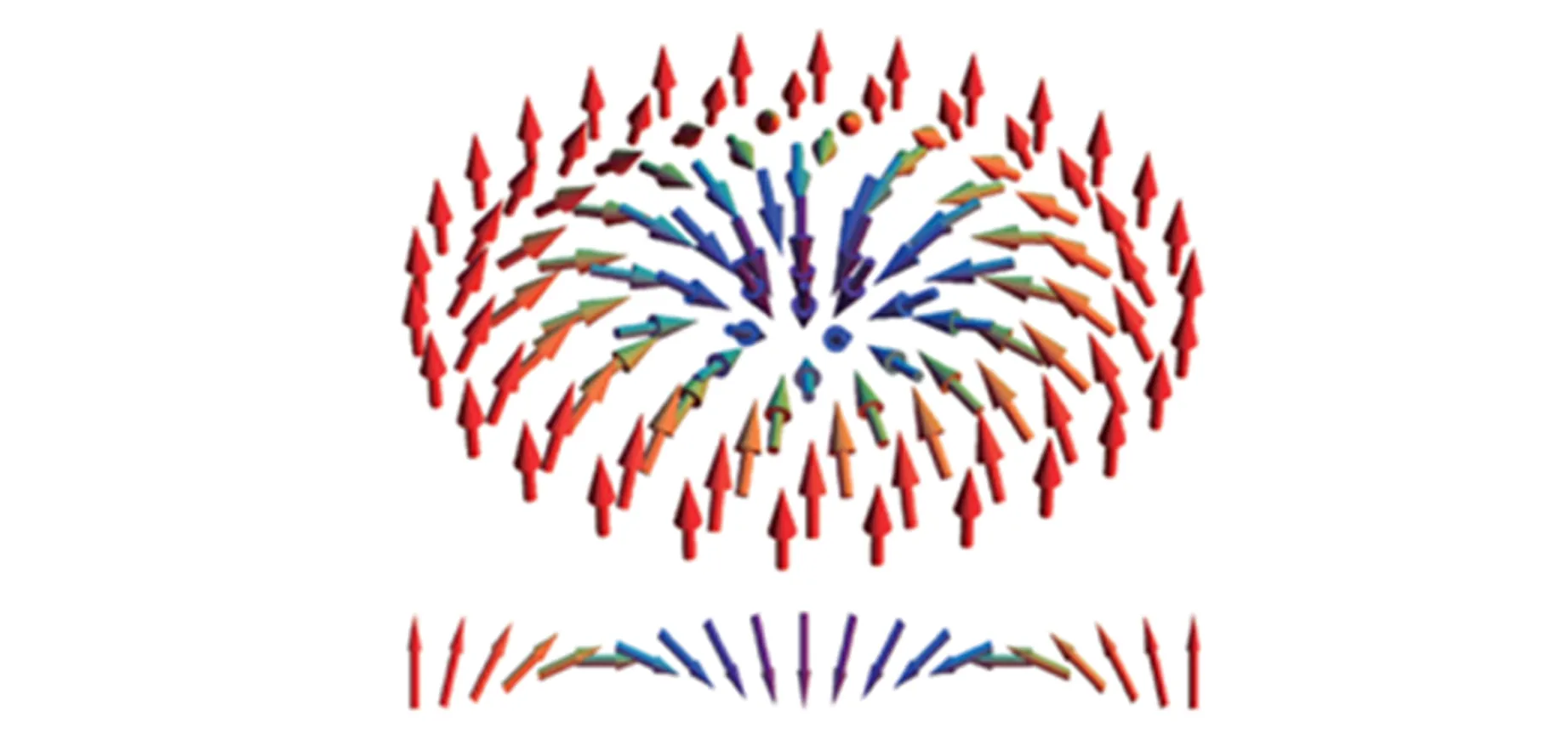
(d) Néel型的斯格明子的自旋结构示意图图3 2类斯格明子结构
1) 对于Bloch型的斯格明子来说,主要出现在中心对称破缺的块体材料中,由于块体材料拥有较强的自旋轨道耦合,能通过DM相互作用使自旋呈非共线排列,所以形成斯格明子 (bulk DMI所诱导的). 对于此类的斯格明子,自旋都是沿着切线方向排列形成涡旋,中心处的自旋方向和边界处的自旋方向成180°排列. 这类斯格明子多数在B20 (FeSi型) 类型的立方晶胞的合金中被发现,空间群为P213,如MnSi[9-11], FeGe[12-13]等材料.
2) 对于Néel型的斯格明子,则多数出现在金属和重金属材料形成界面的多层膜中. 由于重金属中一般会存在比较大的自旋轨道耦合作用,界面处会存在较强的DM相互作用,所以导致了Néel型的斯格明子出现(interface DMI导致的). 这类斯格明子中,自旋都是沿着径向方向旋转. 中心处的自旋方向和边界处的自旋方向也是成180°排列.
以上所提到的2种不同类型的斯格明子,他们不同的自旋结构主要是由于DMI的方向不同所导致的. 一般来说,对于界面DMI所诱导出的Néel型的斯格明子,在实验方面更容易实现调控. 因为斯格明子可以形成非常小的尺寸,如在单层厚度的Fe成长在Ir(111)[14]上,由于界面处的DM相互作用,斯格明子以正方形的格子出现[如图4(a)所示[14]],实验报道其尺寸只有原子量级. Stefan Heinze等人利用自旋极化扫描隧道显微镜 (SP-STM) 直接观测,给出了实空间的自旋非共线的磁结构,图4(c)[14]展示了自旋沿着面外方向的分量图. 斯格明子半径在1 nm的量级,并且能用很小的电流去驱动. 这种小尺寸低能耗的斯格明子, 对未来发展数据存储器件或者其他的自旋电子器件来说能称得上是非常好的备选材料. 而寻找小尺寸低能耗的斯格明子材料也是研究人员一直努力的方向.
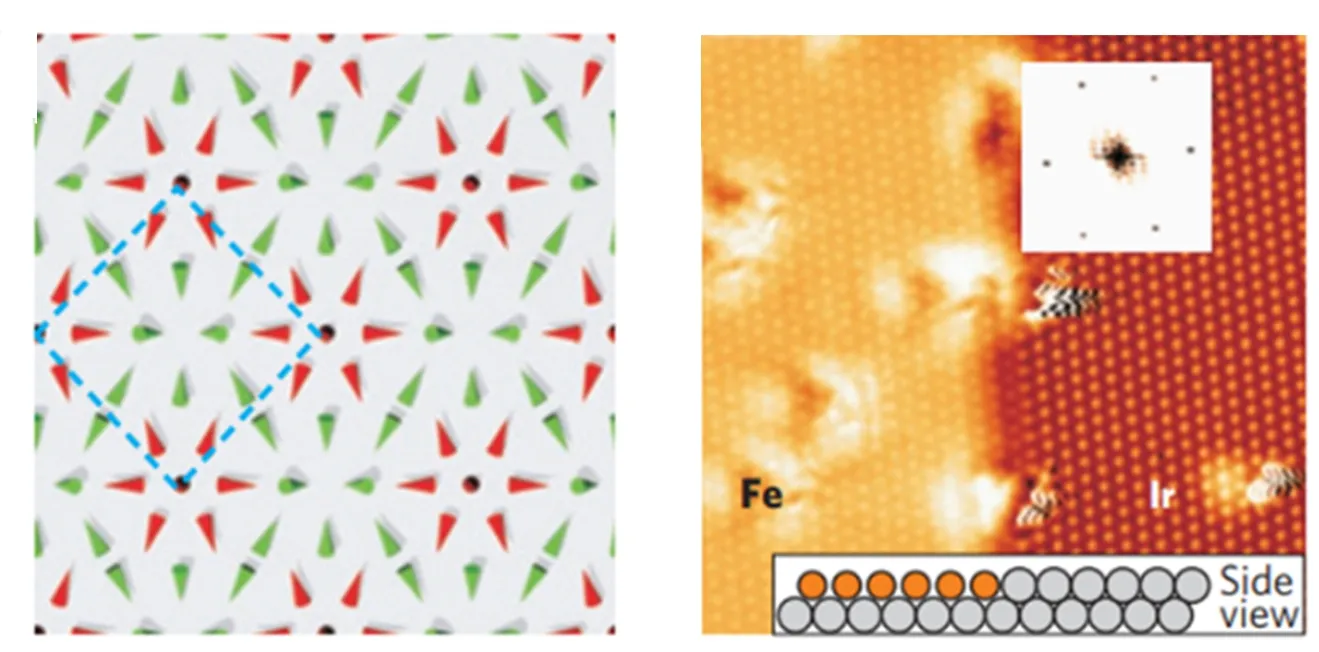
(a) 纳米尺度的斯格明子结构示意图(锥形结构表示Fe原子的位置,箭头的指向代表了其磁矩的指向) (b) 原子尺度下的STM图像
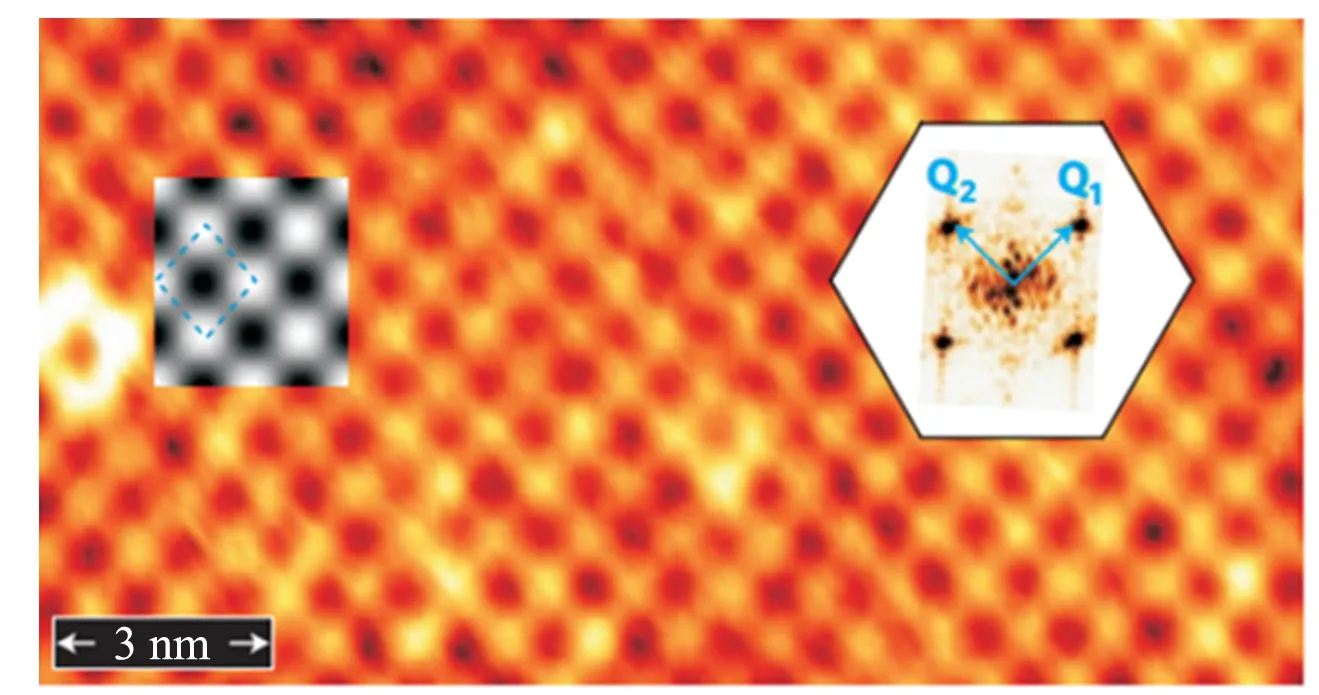
(c) SP-STM图像,磁针可以探测到面外方向的磁化强度,白色和黑色的点分别代表磁矩平行或者反平行于探测磁针

(d) 磁针沿着不同方向时所得到的SP-STM图像图4 生长在Ir的(111)面上的Fe单层中出现的斯格明子
1.2 半导体材料中的斯格明子
前面所提到斯格明子材料都是金属性的,金属性的材料具有导电性,若想通过某种手段实现对斯格明子的驱动,只能用通电流的方式来实现. 而电流在一般的导体中传输都伴随着焦耳热的产生,在调控的过程中无疑会产生很多的能量消耗. 但是,如果通过外加电场对斯格明子实现调控则可以很好地解决这个问题,这样会大大节省电能. 基于之前所发现的斯格明子材料都是金属性的,那么首先要寻找半导体材料才可能会实现用电场来调控的目的. 并且由于斯格明子在对称性破缺所导致的手性相互作用体系中才会出现,所以此类的半导体材料可能也会伴随着铁电性的存在,为实现电场调控提供了可能.
基于如上所述的美好愿景,2014年似乎是迎来了转机. Seki等人在半导体材料Cu2OSeO3中也发现了斯格明子相[15-16],其结构如图5(a)所示[15]. Cu2OSeO3的空间群是P213[15],和B20型的合金材料具有相同的对称性结构. 不过因为Cu2OSeO3是三元的化合物,Cu2+以3∶1的比例被四面体和三面体包围在中间,所以结构属性和其他二元合金类的材料不相同,这也预示了其磁性结构与以往的B20型合金材料可能会有所不同. 其中子散射的结果表明[图5(b)[15]],在60 K以下的温度区域,其磁性为亚铁磁. Y. Tokura等人通过洛伦兹透射电子显微镜观测到了外加磁场为H=0.08 T的实空间的斯格明子自旋结构图. 图5(c)~(d)[15]分别展示了低温下块材和薄膜的磁性相图,可以看到块材中斯格明子相出现在比较小的区域内,但是在薄膜 (厚度约100 nm) 中斯格明子相出现的区域更大.
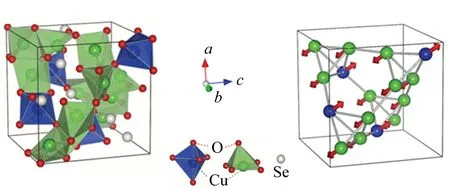
(a) Cu2OSeO3的晶体结构 (b) Cu2OSeO3中的亚铁磁序
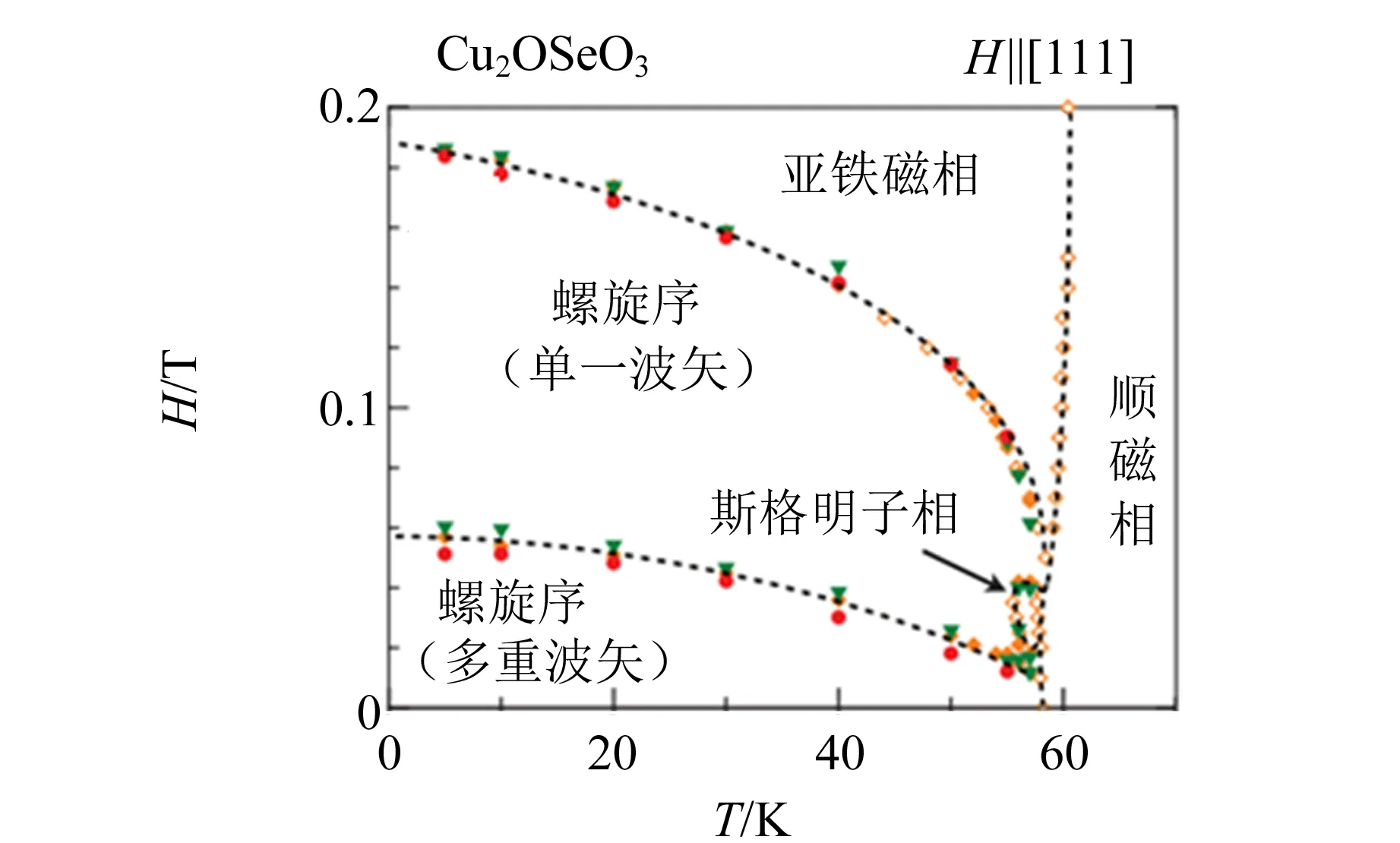
(c) 外加磁场平行于[111]方向时,通过测量磁化强度、电极化大小以及磁化率给出的块材的低温磁性相图
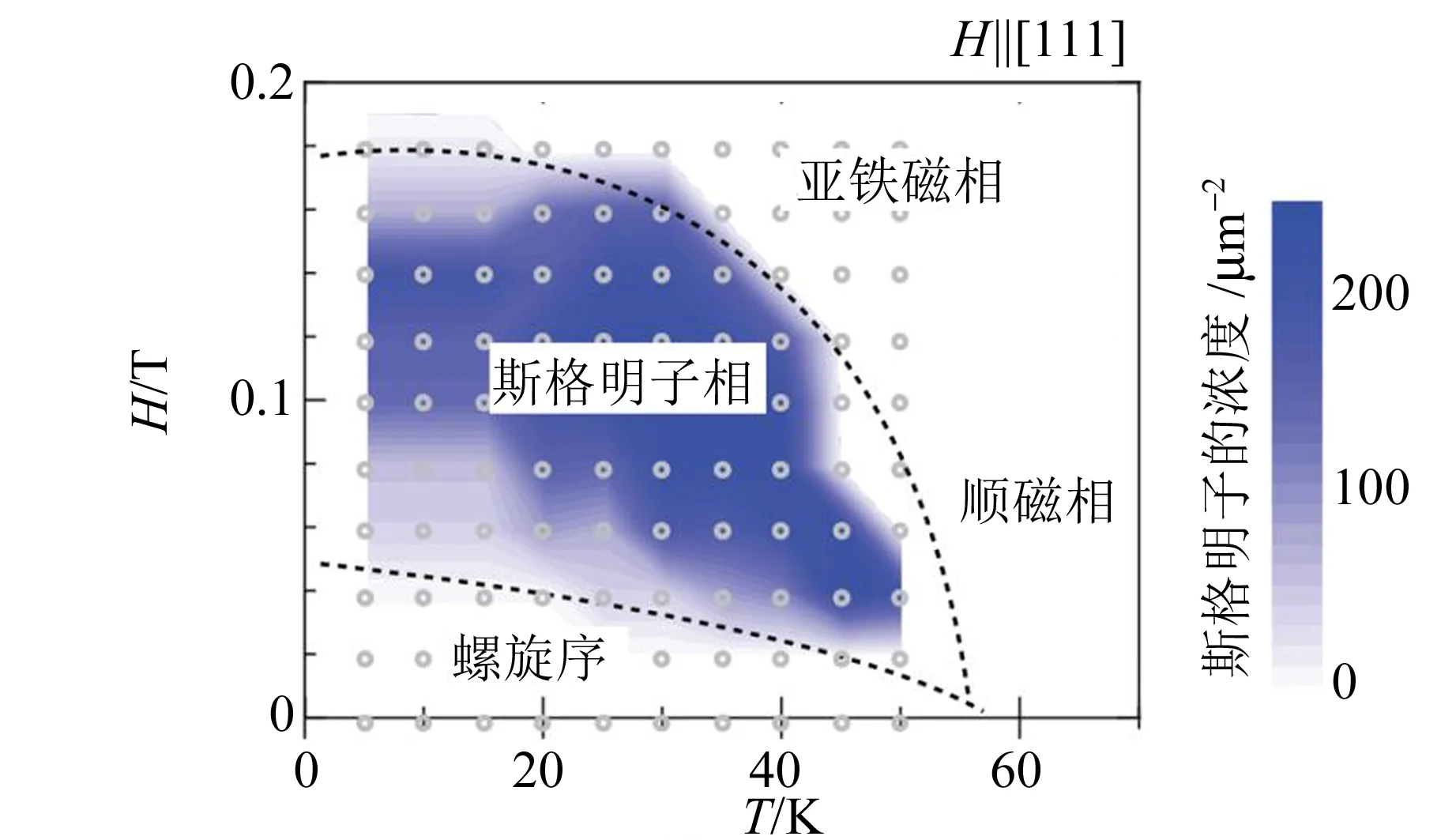
(d) 外加磁场平行于[111]方向时,运用洛伦兹TEM给出的薄膜的低温磁性相图图5 Cu2OSeO3中发现的斯格明子相
正如前述,在存在斯格明子的半导体材料中也极大可能会伴随着铁电性的存在. 所以Cu2OSeO3不但具有半导体的属性,同时又是具有铁电性的[17]. 该研究说明了在立方的B20类型的手性材料中,不管铁磁或者亚铁磁、金属或者半导体,都可能存在斯格明子相,并不局限于铁磁金属材料中才可以存在. 该项发现为研究斯格明子拓宽了视野,使大家在寻找斯格明子材料时能着手于更大的范围.
既然Cu2OSeO3是半导体,并且在体系中同时存在铁磁性和铁电性,那么能不能实现磁电耦合便是人们非常关注的问题,也是该体系最特殊的地方. 在Y. Tokura等人通过测量到的H-P曲线发现,该材料中存在很强的磁电耦合[15]. 也就是说在该材料中,可以通过磁场调节体系的极化强度,也可以通过外加电场调节材料的磁性. 而且无论是此体系中存在的亚铁磁相,还是螺旋相,亦或者是斯格明子相,都存在磁电耦合现象. 图6(d)~(f)[15]给出了不同磁结构所对应的极化的方向. 在这样磁电耦合的体系中可以通过空间梯度电场对斯格明子进行调控,并且无焦耳热的产生,相对磁场驱动会更加节能. 所以,这一重要发现为研究斯格明子指明了更加光明的道路. 在多铁材料中寻找斯格明子相,以期利用磁电耦合的特殊性质设计出高效节能的自旋电子器件.
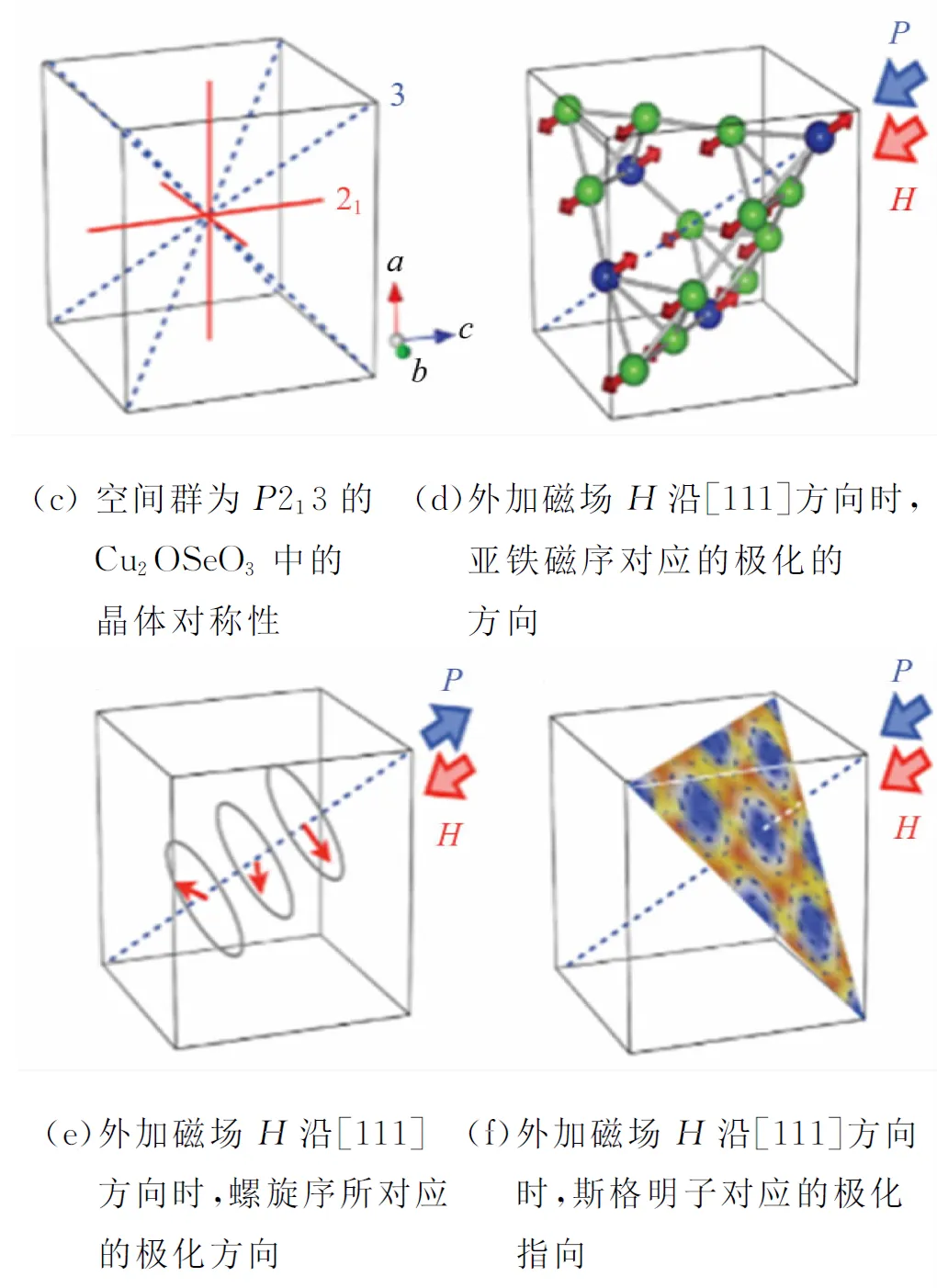
图6 Cu2OSeO3中的磁电耦合示意图
斯格明子的概念虽然很早就被提出来了,但被广泛研究也只在近10年的时间,距离真正地在器件中实现应用还有很长的路要走. 不过这是10年间,斯格明子从第一次在实验中被观测到,到发现微尺寸高密度的斯格明子材料,再到在半导体的磁电耦合材料中被发现,以及室温的斯格明子被报道[18],这些重大的发现一次次带给众多关注它的人以惊喜,也让我们对它以后的研究进展有着特别大的期待.
2 尖晶石GaX4M8(X=V,Mo;M=S,Se)中的斯格明子研究
前面简要介绍了斯格明子的研究进展,其中提到了一类具有铁电性的斯格明子材料,现介绍另外一类具有代表性的存在斯格明子的半导体铁电材料. 通过调研发现,在前人的理论研究报道中曾指出具有Cnv对称性的晶体也是可以存在斯格明子相的[19-21],该类材料引起了我们的关注并做了进一步的相关研究工作. 以下将以GaX4M8(X=V, Mo;M=S, Se)[13,22-26]体系为例说明.
GaX4M8则刚好是具有C3v对称性的一类材料. 作为具有铁磁性的GaV4S8,是第一个被报道存在着斯格明子相的材料[12]. GaV4S8也具有铁电性,实验上所测得的极化在1 μC/cm2的量级. 从这一点上来说,在这样铁磁铁电共存的体系里面,通过电场对斯格明子的驱动和调控提供了极大的可能性. 从应用角度来说,GaV4S8体系中存在各种有利条件,包括实验室所得到的斯格明子的结构尺寸也相对较小,直径约为22.2 nm. 不过不得不提的是斯格明子相出现的区域却非常狭窄,如图7所示[12]. 虽然后续也有其他的文献对GaV4S8体系中的斯格明子进行了报道:一是斯格明子相出现的区域并没有明显增加;二是其基态究竟是螺旋序还是铁磁序亦或者是二者共存的仍然存在诸多争议[12,27-28].
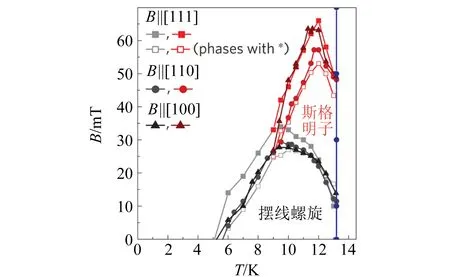
图7 外加磁场作用下GaV4S8的低温磁性相图
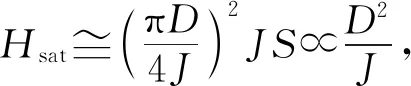
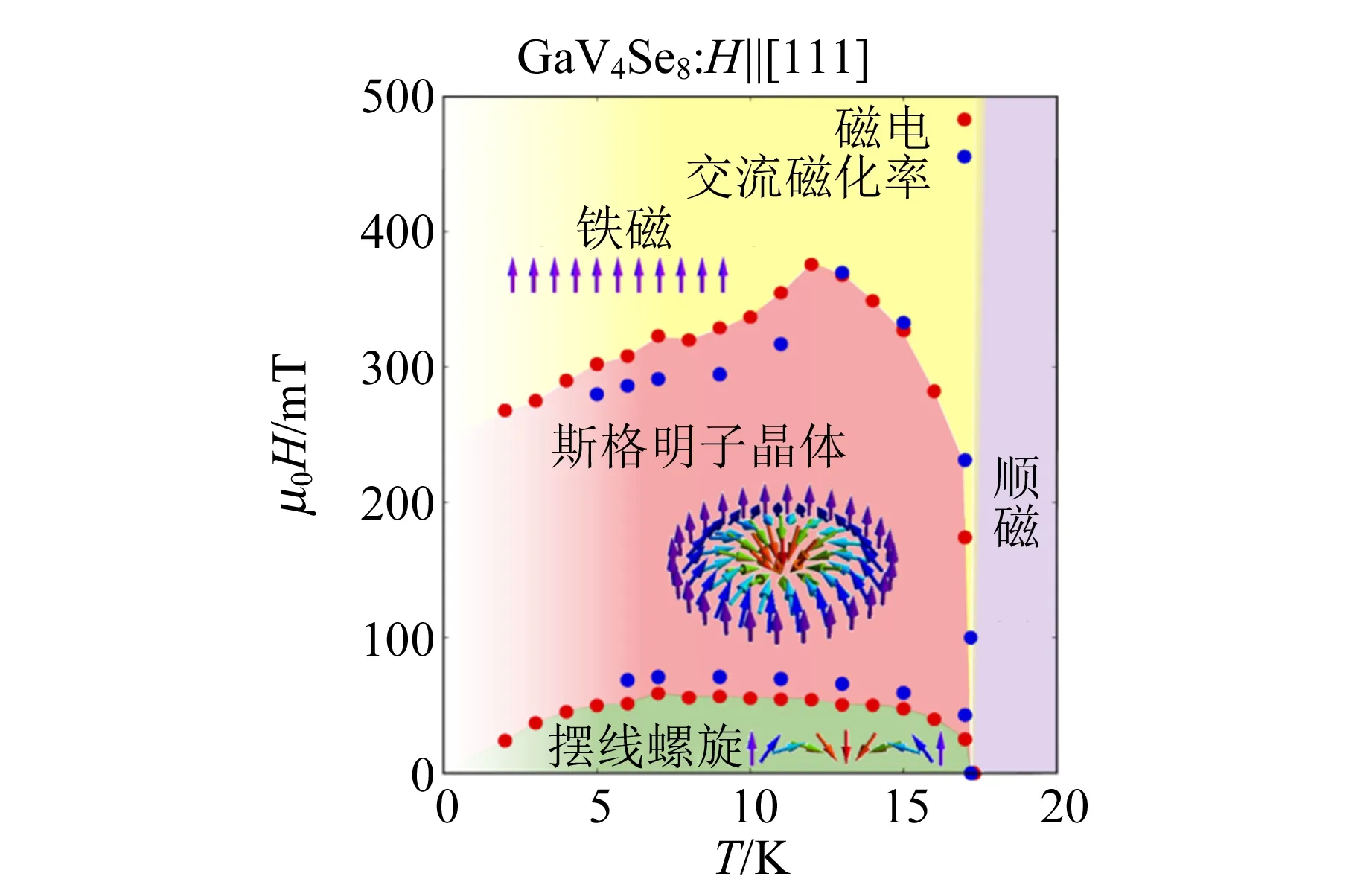
图8 通过在单晶中磁化率和磁电的测量得出外加磁场沿着材料极化的方向 (即[111]方向) 时GaV4Se8的H-T低温相图
受此思路影响我们后续展开了对GaMo4S8的低温磁性的研究. 因为Mo是属于4d电子,具有比3d电子的V更强的自旋轨道耦合作用. 虽然较强的自旋轨道耦合对DM相互作用的增强比较有利,但是也会使磁各向异性的相对增强,使自旋趋向于沿易磁化轴的方向排列而不易形成非共线的磁序. 如上所述,从GaV4S8到GaV4Se8的研究给我们提供了研究思路,但是不得不说斯格明子相的出现是由交换作用J和DM相互作用矢量D以及磁晶各向异性异性能所共同决定的. 寻找自旋轨道耦合相对较强的体系只是一个研究方向,具体能不能发现斯格明子相的存在,还要看体系中各项相互作用相互竞争的结果究竟如何.
3 铁电材料GaMo4S8中的斯格明子相
3.1 背景介绍
具有C3v对称性的GaV4S8和GaV4Se8中都被报道可以存在斯格明子相. 承接之前的研究思路,选择GaMo4S8做仔细的研究,因为其含有自旋轨道耦合相对更强的4d元素Mo. 最初GaMo4S8被报道是铁磁性,居里温度为19.5 K,而且在最近的一些理论计算的文章中也被提到其基态磁性为铁磁的[31]. 不过参考GaV4S8相关研究,它最初也是被报道为简单的铁磁性材料,只是后来多篇文献报道了其低温复杂的磁性[12,27,32]. 关于GaMo4S8中的磁性的研究非常少,对其低温磁性相图的研究是很有必要的. 并且在研究中也和V元素的体系进行了相关对比,给出了3d和4d体系的AM4X8中存在的相似与不同.
据文献报道,在温度降低的过程中,当温度为45.5 K[33](另一文献为47 K[34]) 时候,由于Jahn-Teller畸变导致GaMo4S8会从立方的高对称的结构(F-43m, No.216) 转变为六角的低对称的结构(R3m, No.160) ,图9(a)给出了低温相结构示意图. 对于高温的立方结构,它是非中心对称非极性的,对应Td点群,4个Mo离子直接形成正四面体结构. 但是低温的六角结构却是非中心对称的极性结构,Mo的四面体结构在[111]方向上被压缩,导致顶点处的Mo离子 (记为Mo1) 和面上的Mo离子 (记为Mo2) 的对称性不再相同,变为C3v的对称性结构. 虽然在GaMo4S8中的Jahn-Teller畸变和GaV4S8(Tc=38 K)[35]以及GaV4Se8(Tc=41 K)[29]中很相似,但是V元素体系中的V四面体结构是沿着[111]方向伸长的,这点和Mo体系中完全不同,所以GaMo4S8中的极化和V的2个体系中的极化是指向相反方向的,如图9(c)~(e)所示.
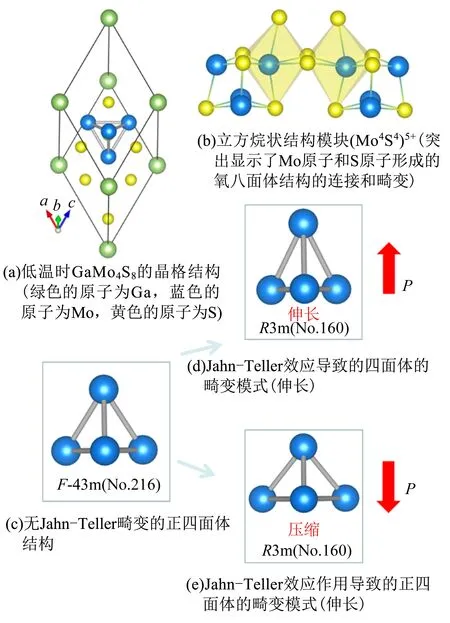
图9 低温下GaMo4S8的晶格结构示意图及结构相变示意图[(d)和(e)中红色箭头代表极化的方向]
3.2 研究方法
应用第一性原理(DFT)计算并结合基于哈密顿模型的蒙特卡罗模拟的方法对GaMo4S8的性质进行了计算. DFT计算的方法,用相对较小的晶体格子,在零温下对材料的电子结构以及磁性性质进行模拟计算. 对外加磁场以及特定的低温区域条件下的磁性结构进行模拟,采用了蒙特卡洛模拟的方法.
为了计算磁性相变,找出磁性相变的温度,计算了比热C和磁矩M. 比热的计算公式为[36]
(1)
式中,H为热能,N是自旋的数量,kB为玻尔兹曼常量,T为温度. 为了对螺旋续和斯格明子相的研究有更深刻的认识,还计算了自旋结构因子(spin factor). 更进一步,为了确定面内的斯格明子的浓度,对χi也做了计算,χi的定义[37]为
(2)
3.3 哈密顿量的建立
在文献[38]中,经DFT计算发现,在GaV4S8中未成对的1 μB的电子主要分布在顶点处V原子上,而平面上的3个V的电子态密度的贡献很小. 但是在GaMo4S8中,顶点处Mo1和平面处Mo2的磁矩为0.21~0.25 μB,这表明自旋密度在Mo4四面体中的分布是非常均匀的. GaMo4S8中出现的这种情况,我们认为是由于4d元素的空间延伸性导致的,使得Mo4四面体中轨道杂化性更强.
把Mo4四面体当做磁性单元[图10(a)~(b)][39],对不同磁性结构进行总能量计算,然后将得到的相关系数绘制在10(c)~(d)[39]图中. 可构造经典的海森堡模型来模拟的哈密顿量:
H=Hex+HDM+HSIA+HZeeman,
(3)
其中
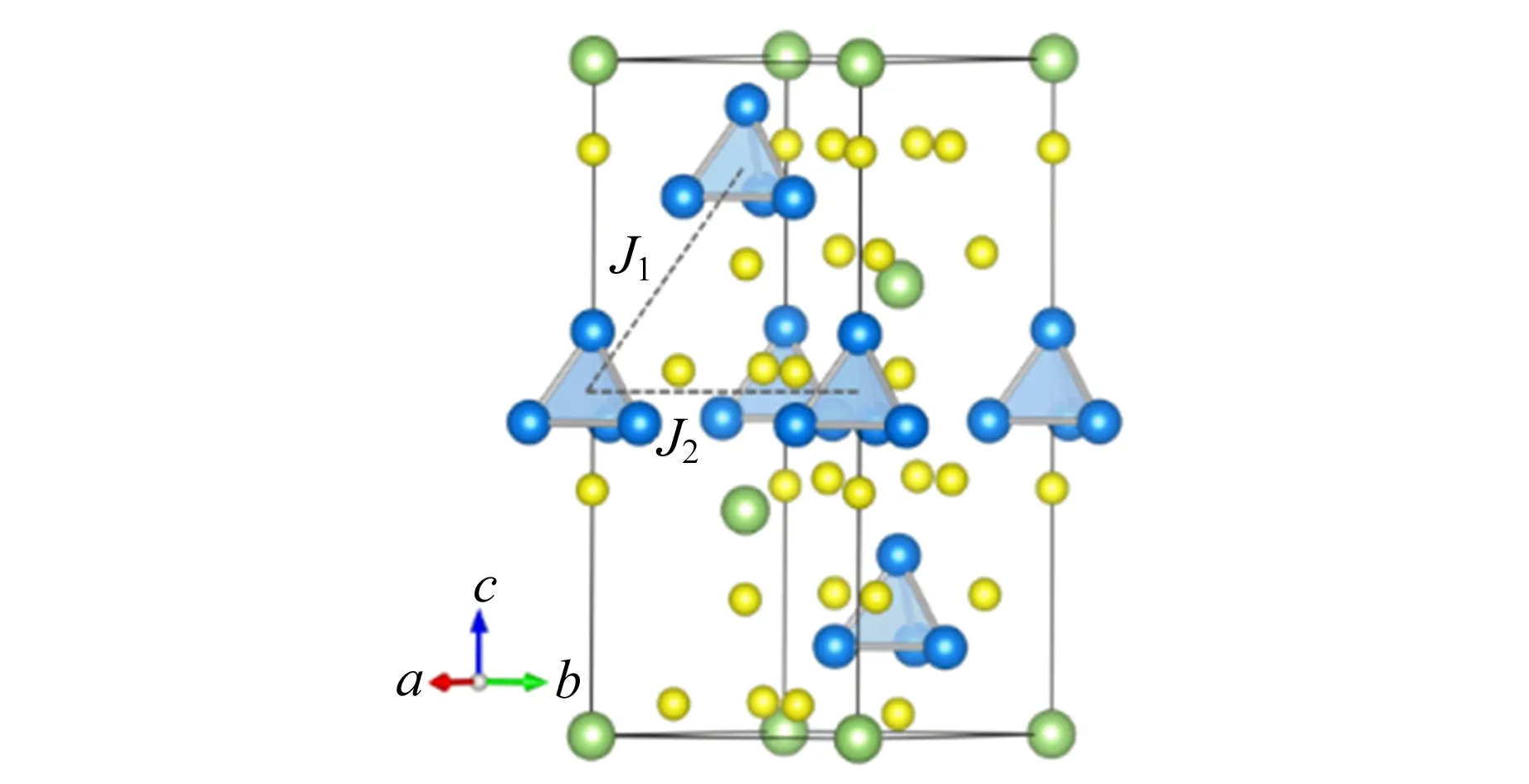
(a)交换作用示意图(面间的磁交换作用用J1表示,面内的磁交换作用用J2表示)
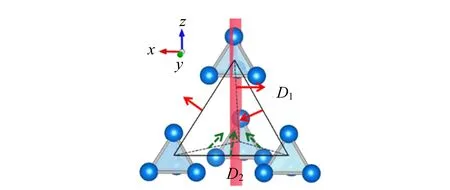
(b) DM相互作用矢量(红色箭头表示面间相互作用矢量,记为D1;绿色虚线箭头表示面内的相互用矢量,记为D2)
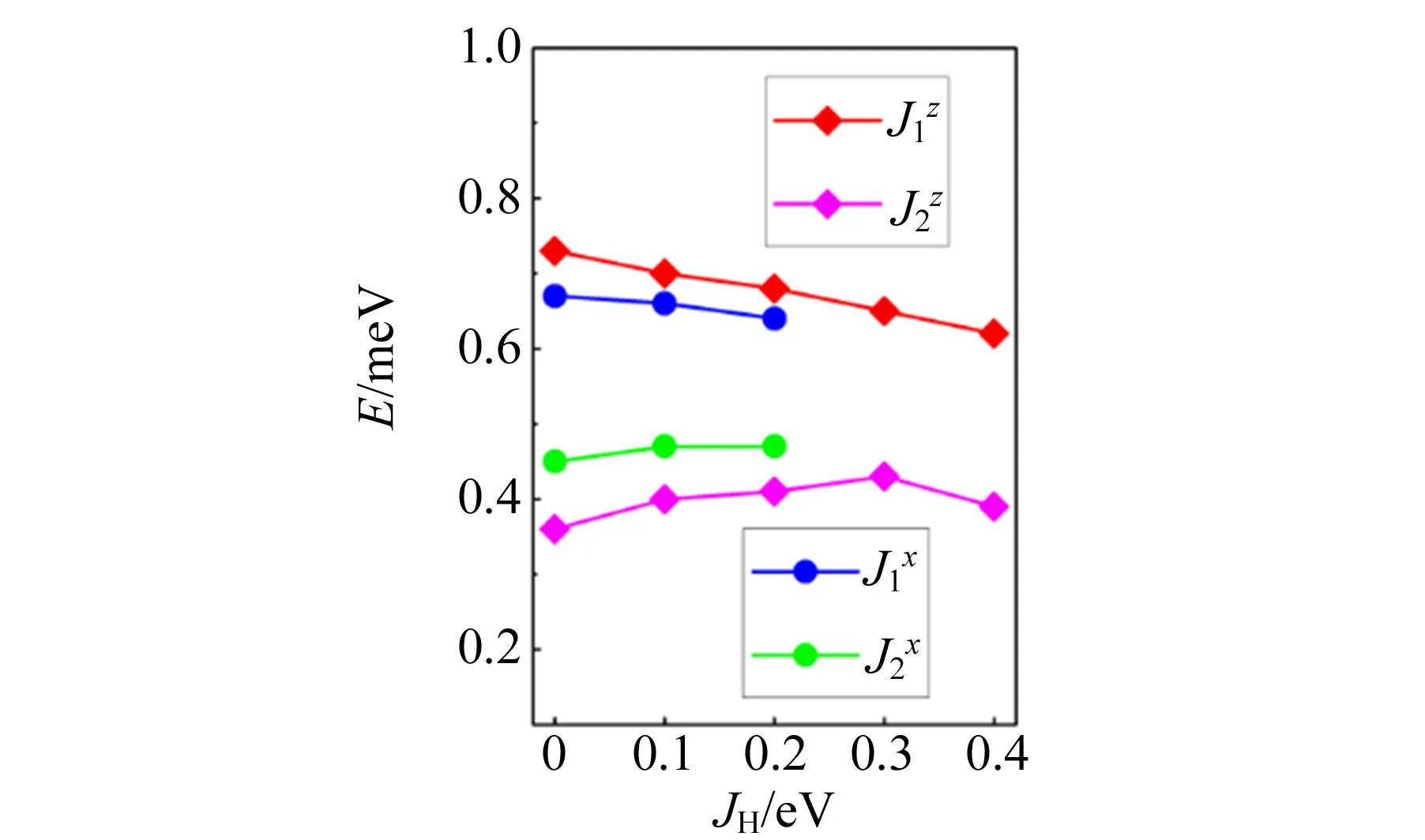
(c)交换作用的大小
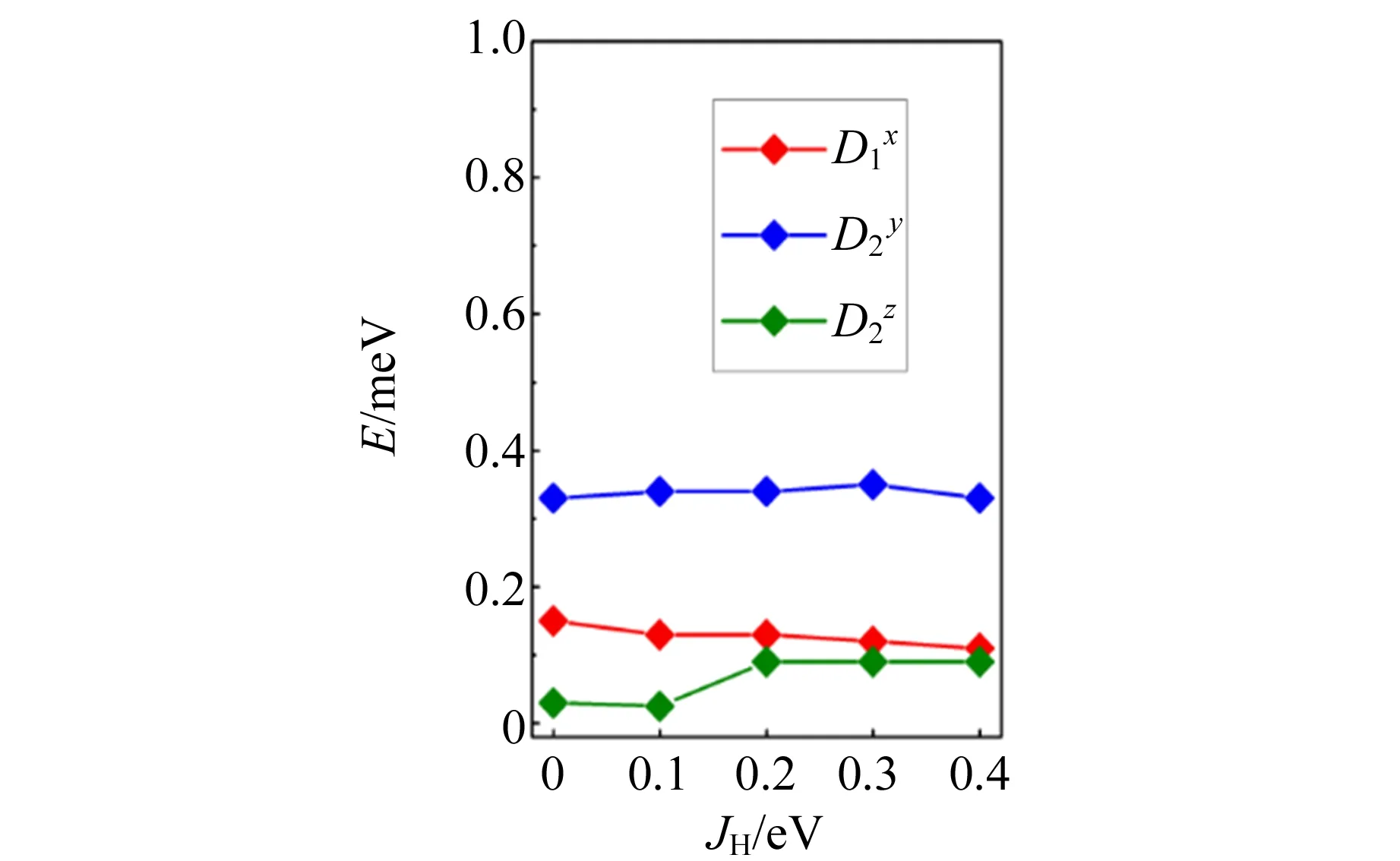
(d)DM相互作用矢量的分量大小图10 GaMo4S8中的磁交换作用和DM相互作用参数的大小(保持U-JH=1 eV,U为库伦相互作用的大小,JH为洪特交换系数)
其中,Si表示在位置i处的归一化的自旋;Hex是考虑到对称性相关的交换作用,采用XXZ型的各向异性模型,J1x和J2x表示自旋指向面内,J1z和J2z表示自旋指向面外;HDM包含了面间和面内两部分相互作用的能量,分别对应D1和D22个矢量;HSIA表示单离子的各向异性,A为其系数;HZeeman为外加磁场h作用下的塞曼能.
3.4 磁性相变
通过蒙特卡洛模拟,可以实现在特定温度下外加磁场对体系的磁性进行研究. 比热曲线的峰值显示磁转变温度[图11(a)][39]出现在19.5 K处,和实验测得的数据基本吻合. 沿z轴方向施加外加磁场,发现ab面内出现的非共线的螺旋磁序[图12(c)][39],其波长约为21倍的晶格参量a,约为14.6 nm. 在垂直于螺旋序出现的面的方向,随着磁场增加该磁序会转变为Néel型的斯格明子相,如图12(d)所示. 随着磁场的继续增加,磁结构会完全转变成铁磁序. 随温度变化,以及施加电场的完整相图如图12(a)[39]所示. 典型的螺旋序结构和斯格明子磁结构,以及自旋结构因子如图12(c)~(d)[39]. 在我们的研究中,斯格明子相的半径预测为6.9 nm,比之前GaV4S8的研究中心所报道的半径 (rV) 11 nm要小很多[12].
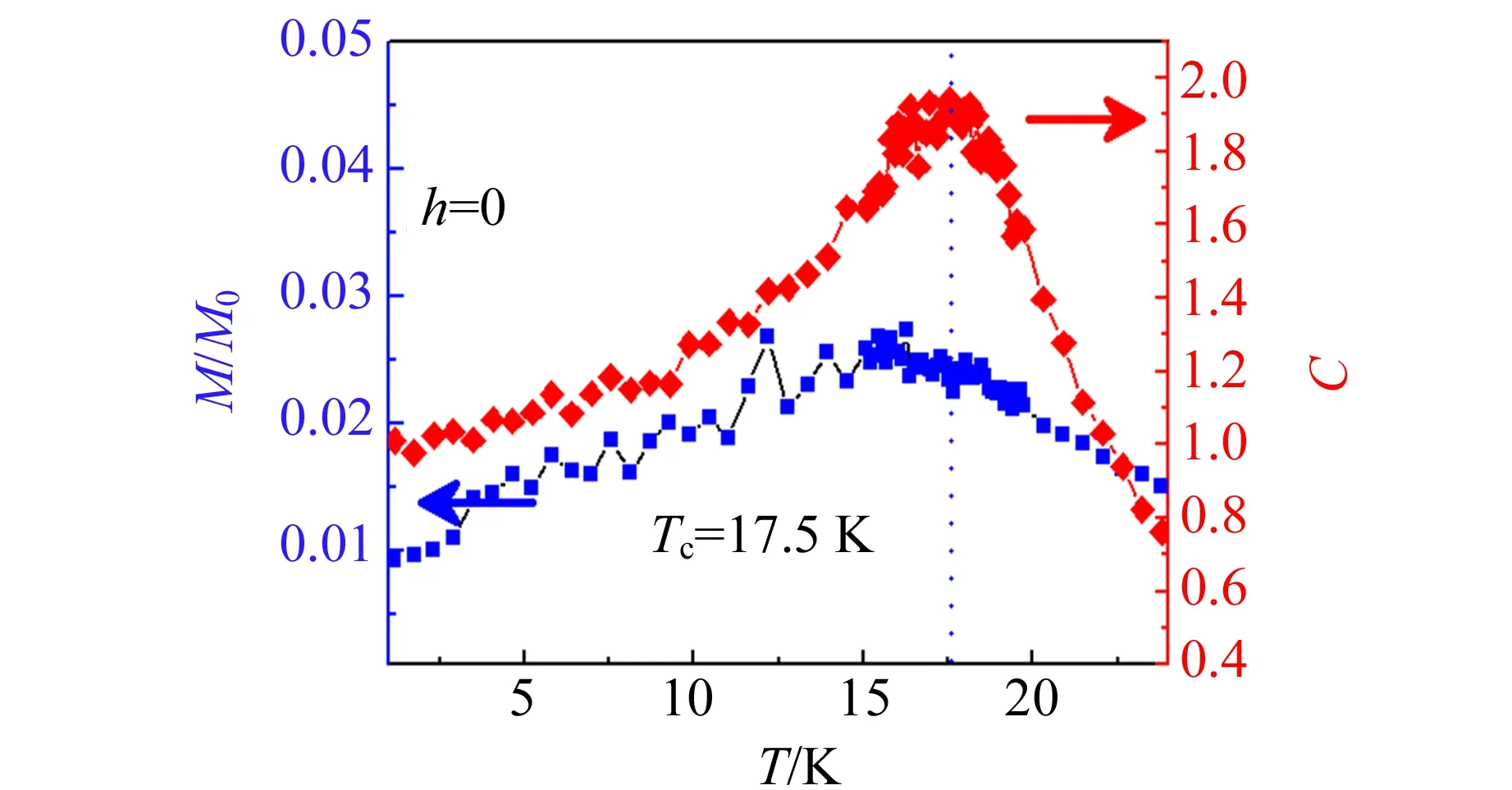
(a)JH=0
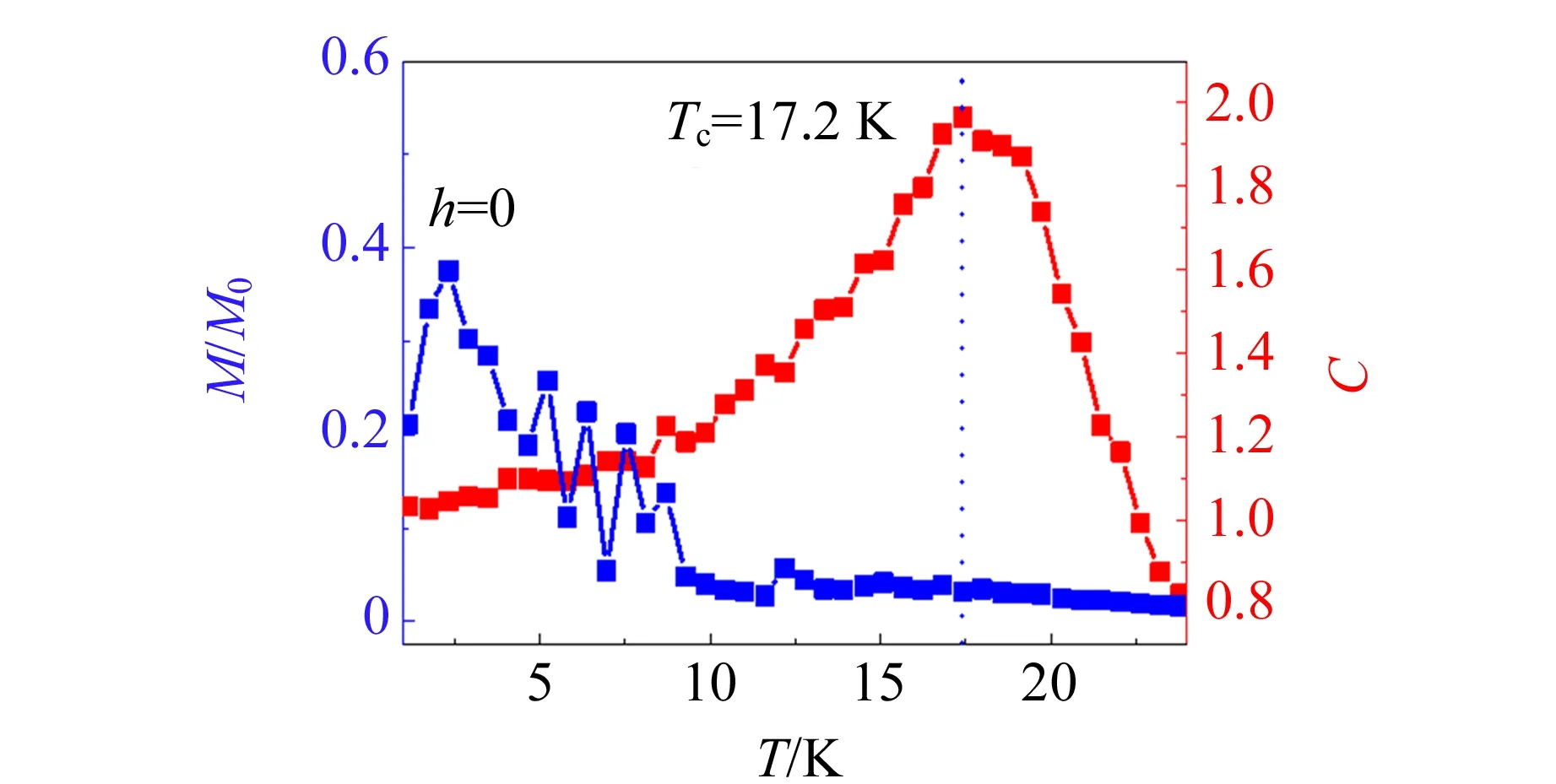
(b)JH=0.1 eV图11 蒙特卡洛计算的结果,低温的磁化强度M和比热曲线C表明材料的基态时非铁磁(JH=0) 或者铁磁性的(JH=0.1 eV)
如上结果中,之所以出现了半径较小以及密度较高的斯格明子相,是由于GaMo4S8体系中较强的自旋轨道耦合效应,并导致的较大的|D|/J比值,这也和我们研究最初的猜想相一致.
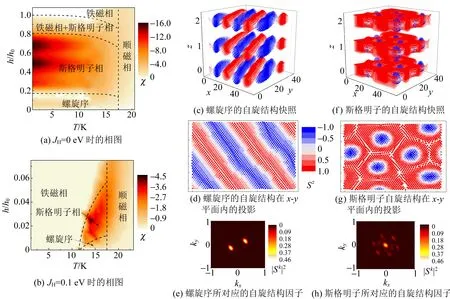
图12 蒙特卡洛模拟得到的相图(自旋结构因子中,白色的点表示对波矢的调制. 2个峰对应螺旋序结构,六重峰对应斯格明子. h0表示低温下的饱和磁化强度.)
3.5 讨论与总结
通过以上研究发现,虽然GaMo4S8和GaV4S8具有非常相似的结构,但其性质不完全相同. 首先,d轨道不同的价电子占据数,在Jahn-Teller效应的作用下导致不同的极化方向. 其次,由于4d轨道的延展性,GaV4S8中V1和V2磁矩出现的歧化作用[38],在GaMo4S8的Mo4四面体中并没有出现. 第三,由于4d元素较强的自旋轨道耦合效应,GaMo4S8中的 DM相互作用比GaV4S8中更强. 正是由于较强的DM相互作用,使得非共线的磁结构更容易出现,而且最近邻自旋之间的角度会更大. 所以,相对应的螺旋序和斯格明子的周期会更小,这在蒙特卡洛模拟中也已经证实.
但是这里也需要指明,自旋轨道耦和并不一定是越强就越有利于斯格明子的稳定. 因为强的自旋轨道耦合还可能会导致磁各向异性的增强,这对非共线结构的形成是不利的. 例如,在JH=0.1 eV比JH=0时磁各向异性显著增强,所以导致斯格明子相出现的区域变小,并且仅仅出现在居里温度以下的高温区域. 所以这样来看,在对斯格明子的研究中,自旋轨道耦合效应其实有利也有弊.
交换作用、DM相互作用以及各向异性能都会对斯格明子的出现有影响. 参考了以往的相关研究,在计算中对相关参量进行了测试,并尽可能选取了接近实际实验预期的参量. 我们的理论预测,在外加磁场作用下斯格明子相可以在GaMo4S8中出现. 并且在相图中斯格明子相被预测到可能会出现在非常大的温度和磁场区域. 希望我们的研究,对在尖晶石或者相类似的体系中去寻找高密度的斯格明子研究提供参考,同时也呼吁相关方面的试验专家可以在实验中进一步研究.
4 展 望
总体来说,至今对斯格明子的研究已经非常多,但是在半导体铁电材料中找寻斯格明子材料依然是非常有意义的研究方向. 因为目前已经被发现的此类材料是非常少数的,而已经发现的这类材料中斯格明子出现的温度都非常低,从应用方面来讲是非常不利的. 所以不断找寻稳定低能耗的斯格明子材料,进一步实现电场直接对斯格明子的调控,才能推动斯格明子研究进程的不断发展,才能为将来自旋电子器件中得以应用提供可能.
