直流电压下植被燃烧颗粒在火焰间隙中的运动分析

2020-04-18普子恒史星涛周晨曲王子鸣黎鹏吴田方春华

三峡大学学报(自然科学版) 2020年2期

普子恒史星涛周晨曲王子鸣黎鹏吴田方春华

(1.三峡大学电气与新能源学院,湖北宜昌443002；2.湖北省输电线路工程技术研究中心,湖北宜昌443002)

我国超、特高压线路不可避免经过高森林火险区域,近年来极端气候导致山火频发,引起多起输电线路跳闸事故.据不完全统计,2011年至2018年期间,广西、湖南、云南等多省电网累计因山火故障导致跳闸的事故均达到百余次[1-2].国家电网公司在2014年制定的重要输电通道风险评估工作方案中,山火为首要考虑的技术要素[3].国内外主要针对山火条件下间隙击穿特性进行了大量的试验研究[4-7],利用模拟导线-板间隙得到不同植被火焰条件下的击穿电压.研究表明山火条件下间隙击穿受温度、火焰电导率和颗粒灰烬的综合影响,火焰条件下间隙击穿电压远低于纯空气条件,且正极性击穿电压低于负极性击穿电压[8-10].但由于植被类型、试验方案、燃烧控制方法等均有不同,且火焰本身受扰动影响因素较多,不同尺度的试验所得击穿特性差异较大；而击穿机理方面主要建立单一因素为主的放电模型,综合考虑多因素相互影响的火焰条件下间隙放电模型较少.

植被燃烧颗粒会受到火焰中带电粒子影响而荷电,输电线路下方的燃烧颗粒物在流体曳力和电场力等因素作用下,飘浮到线路下方空间,进一步形成较大颗粒链并桥接部分间隙,同时颗粒在输电线路下方漂浮时会使局部电场畸变发生放电,进而造成整个间隙击穿[11-12].首先分析颗粒荷电情况,许多学者对于风沙荷电、静电除尘方面的颗粒荷电进行了大量研究.刘云鹏、耿江海等分析了沙尘荷电的机理,并通过试验探究了沙尘等因素对空气间隙击穿的影响,结论表明在短间隙内,荷电沙尘会降低击穿电压[13-15]；王宇、姚强等分析了在电场下碳氢化合物燃烧的小尺寸火焰中碳烟颗粒的浓度分布及荷电特性,并验证了颗粒多数荷正电[16-18]；高梦翔、蔡杰等对流体场中颗粒运动进行了数值分析,通过多场耦合计算得到了不同情况下的颗粒运动轨迹[19-20].但模拟输电线路下方植被燃烧的颗粒情况更为复杂,其运动轨迹及规律的研究较少,现有研究主要分析了颗粒均匀分布的电场畸变情况[11-12].空间中正负极性的荷电颗粒其运动轨迹也有较大差异,因此需要建立合理的仿真模型,分析不同极性燃烧颗粒的运动轨迹和分布规律.

为此,本文结合典型植被燃烧特征量,提出温度、流体、电场和颗粒运动的多物理场耦合仿真方法.根据实测的植被火焰产热率,通过流体与温度场的耦合计算,得到了植被火焰的温度分布和流体运动特性.根据流体运动特性计算颗粒所受流体曳力,结合颗粒荷电特性计算电场力,加上重力作用共同得到燃烧颗粒在间隙中运动的受力变化,对比分析颗粒荷电极性、荷质比、初始位置以及粒径大小等因素对燃烧颗粒受力和运动的影响.

1 燃烧颗粒运动的多物理场仿真方法

1.1 多物理场耦合仿真方法

植被火焰燃烧时热气流和颗粒灰烬可看作气固两相体,同时考虑火焰体部分可看作等离子体区域,颗粒灰烬也会荷电,在正、负极性直流电压作用下,火焰体本身和颗粒灰烬都会受到电场的影响,整体的运动更为复杂.分析颗粒的运动规律,首先分析颗粒的受力情况,在燃烧热气流作用下的热涌力、压力梯度力以及飘浮过程中的浮力、Saffman力等量级很小,颗粒主要受流体曳力、电场力和重力的综合作用.

重力为一定值,主要分析流体曳力和电场力情况.根据电场分布特点可知,越靠近电极电场越强,所受电场力越大,而在植被附近受热气流作用更强.计算颗粒所受流体曳力,需要计算植被火焰的流体场,此处由于颗粒占比较小,简化处理暂不考虑颗粒对流体的作用,主要考虑温度和流体场的耦合作用,而温度场计算则以试验测量的植被热释放率和温度分布为依据.计算颗粒所受电场力,首先要考虑颗粒的荷电情况,火焰体为等离子体且温度高,颗粒、灰烬容易产生热电离或吸附带电粒子,但当颗粒到达上方烟雾区后,由于复合作用荷电颗粒量迅速减少,暂时不考虑在上方烟雾区荷电颗粒对背景电场的影响；同时火焰体区域可看作高阻区域,可根据试验测量的等效电阻率设置对应火焰区域.根据上述设置情况建立流体、温度、电场和颗粒运动的多物理场耦合模型,分析流程图如图1所示,其中不同植被的颗粒尺寸可根据相关试验结果进行设置.

1.2 颗粒受力的数学模型

对燃烧颗粒综合受力的数学模型进行讨论.首先分析流体曳力,火焰燃烧产生的热气流为典型湍流,而植被火焰从点燃到熄灭经历多个阶段,仿真主要考虑最容易产生击穿放电的稳定燃烧阶段.在对比于标准模型后,采用了更适用于模拟燃烧涡旋的重整化群(RNG)κ-ε模型,此模型中包含了低雷诺数流动效应和旋流修正模型,其控制方程见公式(1)～(2):

式中:κ 为湍流动能；ε 为湍流耗散率；σκ和σε分别为κ 和ε 的湍流普朗特数；Cε1和Cε2为计算常数.

通过该模型求解湍流粘性系数和动量方程.然后根据斯托克斯定律中的曳力公式来计算颗粒受到的曳力大小,见公式(3):

式中:FD为牵引力；mp为颗粒质量；u为颗粒速度；v为流体速度；τp为影响因素；ρp为颗粒密度；dp为颗粒直径；μ为动力粘度.

考虑颗粒所受电场力,首先考虑颗粒荷电情况.碳氢化合物燃烧反应区离子浓度约为109～1011/cm3,一般离子浓度在1010/cm3.而植被中含有大量碱金属和碱土金属,占植被干重的0.05%～3.0%,其电离能较低,如钾盐为4.34e V.在高温下碱金属及碱土金属盐和电离能为4.35 eV的炭黑颗粒都易发生热电离.植被燃烧时碱金属和碱土金属随热流卷入高温区发生热电离,增大了火焰间隙的离子数目,火焰中的离子浓度可增加到1012/cm3.考虑到火焰体内蕴含着丰富的带电粒子,颗粒很容易达到其饱和荷电量,颗粒饱和荷电大小见公式(4),对应电场力FE见公式(5):

式中:ε0为真空介电常数；εr为颗粒相对介电常数.

由公式可知,在颗粒运动过程中,饱和荷电量不是一个定值,会随电场强度变化.同时在靠近电极过程中,电场强度也会增大,受到的电场力也会相应增大.加上电场力和重力G,颗粒所受总力为:

1.3 仿真模型参数设置

植被燃烧条件下间隙的区域划分为植被叶垛、火焰等离子区域和烟雾区域,如图2所示.由于仿真模拟涉及多个物理场,如果采用三维模型,流体场和颗粒运动场的耦合计算量大且较难收敛,考虑本文为初步规律性分析,先采用简化二维模型进行仿真求解.火焰体和棒电极可看作轴对称模型,根据试验布置设置植被叶垛区域半径为12 cm,高10 cm.根据不同植被火焰区域测量的电阻率,将等效火焰稳定燃烧的高阻区域设置为一个对应尺寸的圆台.上方棒电极半径为1.5 cm,长度15 cm.同时设置外空气包的半径为100 cm,高度为200 cm,外边界设置为开放边界.

颗粒设置从植被表面产生,本文主要研究小尺寸颗粒的影响,此处将颗粒简化为球形颗粒,通过试验测量得到颗粒的质量范围见表1.根据文献[21]中典型植被的燃烧试验,得到典型植被燃烧的热释放速率和颗粒尺寸统计规律,作为仿真的基本参数,同时测量火焰温度分布作为对比数据.

表1颗粒粒径及对应质量

2 仿真结果与分析

2.1 温度分布仿真结果对比分析

结合文献[21]中试验测得的植被热释放率,按不同比例设置在植被区域和稳定燃烧区域,选取最接近实际温度分布的分配比例.以秸秆为例,其热释放速率为15.93 kJ/s,根据测量结果设置火焰稳定燃烧区域高度为20cm,设置气体为可压缩气体,考虑重力影响.选取合适的分配比例,瞬态分析结果中某一时刻的温度分布,如图3所示.最高温度在500℃左右,与试验结果接近.植被叶垛附近的温度低于外部火焰区.从火焰稳定燃烧区域向上,温度逐渐降低,分布规律与试验结果较为一致,对比结果见表2.

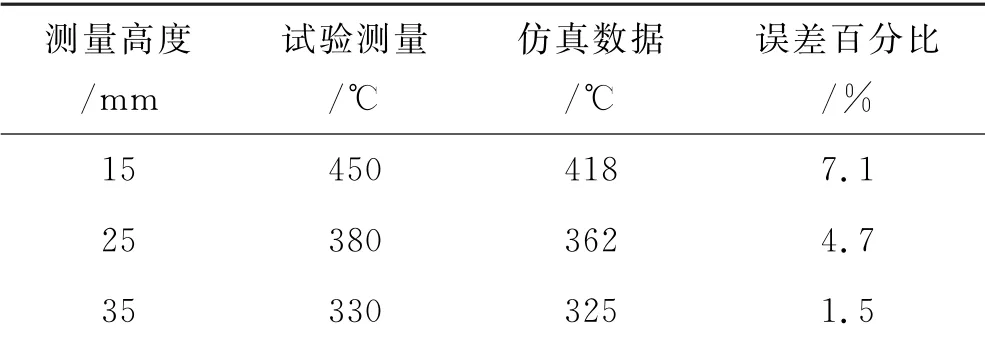
表2火焰温度对比

2.2 燃烧颗粒的运动和受力分析

棒电极设置50 k V 正极性直流电压,燃烧颗粒设置不同的质量、电荷极性和对应荷电量.沿植被区域边缘选取5个颗粒初始位置,分析颗粒的运动轨迹,荷电为正极性和负极性的情况下颗粒的运动轨迹如图4和图5所示.

可以看到当颗粒荷电极性与电极相同时,初始阶段燃烧颗粒受电场力较小,主要受流体曳力影响,颗粒随热气流上升,同时缓慢向外扩散.当接近电极附近的高度时,电场会增大,在电场力的作用下颗粒迅速向外移动.越靠近棒电极,电场力越强,向外移动速度越快,当远离电极后向外移动又变缓.当燃烧颗粒的极性与电极的极性相反且接近电极附近的高度时,颗粒向棒电极移动.颗粒带有一定电荷量时,当其与电极小于一个临界距离,颗粒会被电极吸附,如图5的1号颗粒.当颗粒在临界距离之外,颗粒会在向电极运动一段距离后将随着热空气流动重新远离电极,如图5的2、3、4、5号颗粒.

颗粒在燃烧的火焰中运动时,其受力始终在不断地变化.电极为正极性时,当颗粒携带的电荷与电极极性相同,则其受力过程如图6所示.

颗粒运动的初期,颗粒在流体曳力作用下向上运动,由于燃烧颗粒密度较小,快速与热气流达到近似速度,速度差较小,其所受到的曳力值也较小.同时上升过程中由于颗粒荷电与电极的极性相同,电场力对荷电颗粒产生排斥作用,颗粒逐渐接近电极时,颗粒所受的电场力增大.同时由于电场力方向与颗粒运动方向相反,使颗粒与流体的速度差增大,进而导致流体对颗粒的曳力增大,最后逐渐达到一个动态平衡,即流体曳力与电场力大致相等,在距离电极最近时达到最大值.

在颗粒运动至电极上方后,由于颗粒所受电场力逐渐反向,颗粒受电场力推动向上运动,在Y轴方向上当电场力大于重力时,颗粒速度会加快,大于流体速度,则颗粒所受流体曳力也会反向,最后电场力和流体曳力会因为颗粒远离电极而逐渐变小.在X轴方向,荷电颗粒受曳力和电场力作用向外运动,在运动到电极附近时,电场力将会增大,使颗粒向外运动速度大于流体速度,流体对颗粒的曳力反向,随后电场力逐渐减小,颗粒所受曳力也随之减小,最后颗粒所受流体曳力与电场力均向外,致使颗粒向外运动.

当颗粒荷电和电极极性相反时,颗粒会受到电极的吸引力,会产生两种情况,当吸引力足够大,则颗粒被电极吸附,而流体曳力如果大于电场力,则颗粒会逐渐飞离电极,两种情况的受力过程如图7所示.

图7(a)中颗粒被吸附至电极上,颗粒向电极运动时,颗粒所受电场力逐渐增大,颗粒所受流体曳力也会对应增加,但流体曳力始终小于X方向的电场力,所以颗粒仍向电极移动,最终被吸附在电极表面；分析Y轴方向受力,初始时颗粒所受流体曳力和电场力均为向上的力,当颗粒速度迅速增大并逐渐大于流体速度过程中,流体曳力先减小随之反向增大.

图7(b)为颗粒未被电极吸附的受力过程,初始运动过程与图7(a)相似,但运动到电极附近时,由于颗粒距离电极较远,其X轴方向上电场力与曳力大小相近,方向相反,因此颗粒不能快速靠近电极,所受电场力不足,颗粒继续飘浮上升,所受X轴和Y轴方向的电场力合力小于总的流体曳力,颗粒逐渐飞离电极.

2.3 颗粒受力影响因素分析

燃烧颗粒的尺寸大小以及在火焰中的荷电不同,其受力和运动过程也不相同.由公式(4),不同尺寸的颗粒最大荷电量是不同的.为综合研究尺寸和荷电量的影响,此处采用相同荷质比进行对比分析,不同荷质比颗粒纵向曳力计算结果如图8所示.由图8可知在颗粒粒径相同的情况下,荷质比越大时,其受到的纵向曳力也会越大,而且越靠近火焰内侧,受到的纵向曳力也越大.这是由于随荷质比增大,颗粒所受电场力越大,对应最大纵向曳力也越大.

通过对不同质量和粒径大小的颗粒在同一荷质比的情况下进行仿真对比分析,如图9所示.可以发现,在电极下方时,颗粒粒径dp越大,曳力需要克服的颗粒自身重力也会逐渐增大,特别是当颗粒粒径大于5×10-5m,颗粒受到的曳力逐渐从主要克服电场力做功变成主要克服其颗粒自身重力做功,所以颗粒粒径越大的时候,颗粒内外侧曳力也越接近.

当相同粒径的颗粒携带不同的荷电量时,不同荷电颗粒荷电量均会向电极运动,受到电场力对颗粒的吸引会缓缓增大,迫使颗粒从外侧向内侧运动,从而产生一个向外的横向曳力.而横向曳力会有一个最大值,如果当电场力仍大于这个横向曳力时,荷电颗粒将不可逆地向电极漂浮,最终可能会被电极捕捉并吸附在电极上,并且可以发现被电极吸附的颗粒其荷质比较大,接近于颗粒满荷电状态,如图10所示.

同时不难看出,离火焰中心越近的颗粒越容易被电极吸附住.由图11可以看到颗粒离火焰中心越远其被电极吸附的临界横向曳力也会逐渐增加,其根本原因在于颗粒荷电量的增大,所以荷电颗粒存在临界荷质比的问题.并且颗粒的临界荷质比会随粒径的增加而逐渐减小.这说明在相同荷质比的情况下,大尺寸颗粒会更容易吸附在电极上,而尺寸较小的荷电颗粒在满荷电的情况下也不易吸附在电极上.

2.4 荷电颗粒的分布规律

颗粒在运动的过程中会受到多个因素的影响,而不同初始位置的荷电颗粒运动轨迹也不一样.燃烧颗粒粒径存在一个统计规律,不同尺寸的荷电颗粒在电极附近的分布规律则会影响到电极附近电场的畸变以及引发电极放电.同极性颗粒的运动是向外扩散的运动,荷电颗粒对电极的影响较小,但异极性颗粒的运动则是向电极方向的,所以本节主要对异极性颗粒在电极附近的分布规律进行仿真分析.

由图12可以看出,在电极附近聚集较多的荷电颗粒,尺寸较大的荷电颗粒大概有80%会吸附在电极上,而尺寸较小的颗粒只有20%左右会被电极捕获,其余的均从电极侧面飘过.这是因为尺寸较大的荷电颗粒其在曳力的作用下运动速度比尺寸较小的颗粒运动速度慢,在经过电极时,产生的横向曳力有足够的时间使得颗粒横向运动到电极上,而较小的颗粒运动速度较快,通过电极时,即使产生了横向曳力使颗粒向电极运动,但颗粒会快速飘过电极向上方运动.被吸附的较大荷电颗粒其颗粒本身所携带的电量也较多,所以在当颗粒靠近电极时就会使电极附近的电场产生畸变,而火焰本身也使得电极附近的空气温度升高,起晕场强降低,所以更容易产生电极对颗粒的放电.